Гамма-функция - Gamma function

Для гамма-функции ординалов см. Функция Веблена. О гамма-распределении в статистике см. Гамма-распределение. Для получения информации о функции, используемой в представлении цвета видео и изображения, см. Гамма-коррекция.

Гамма-функция вдоль части действительной оси

В математика, то гамма-функция (представлена ${displaystyle Gamma ,}$ заглавная буква гамма от Греческий алфавит ) - одно из часто используемых расширений факториальная функция к сложные числа. Гамма-функция определена для всех комплексных чисел, кроме целых неположительных. Для любого положительное число ${displaystyle n,}$

${displaystyle Gamma (n)=(n-1)! .}$

Получено Даниэль Бернулли, для комплексных чисел с положительной действительной частью гамма-функция определяется через сходящуюся несобственный интеграл:

${displaystyle Gamma (z)=int _{0}^{infty }x^{z-1}e^{-x},dx, qquad Re (z)>0 .}$

Тогда гамма-функция определяется как аналитическое продолжение этой интегральной функции к мероморфная функция то есть голоморфный во всей комплексной плоскости, кроме нуля и отрицательных целых чисел, где функция имеет простой полюса.

У гамма-функции нет нулей, поэтому обратная гамма-функция ${displaystyle 1/Gamma }$ является вся функция. Фактически гамма-функция соответствует Преобразование Меллина отрицательного экспоненциальная функция:

${displaystyle Gamma (z)={{mathcal {M}}e^{-x}}(z).}$

Существуют и другие расширения факториальной функции, но гамма-функция является наиболее популярной и полезной. Это компонент в различных функциях распределения вероятностей, и как таковой он применим в областях вероятность и статистика, а также комбинаторика.

Мотивация

Гамма-функция интерполирует факториальную функцию к нецелым значениям.

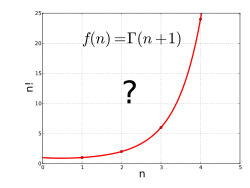
Гамма-функцию можно рассматривать как решение следующих интерполяция проблема:

"Найти плавная кривая что соединяет точки${displaystyle (x,y)}$ данный ${displaystyle y=(x-1)!}$ при положительных целочисленных значениях для${displaystyle x}$."

График первых нескольких факториалов показывает, что такую ​​кривую можно нарисовать, но было бы предпочтительнее иметь формулу, точно описывающую кривую, в которой количество операций не зависит от размера${displaystyle x}$. Простая формула факториала, ${displaystyle x!=1 imes 2 imes cdots imes x}$, нельзя использовать напрямую для дробных значений ${displaystyle x}$ поскольку это действительно только тогда, когда Икс это натуральное число (или положительное целое число). Условно говоря, таких простых решений для факториалов не существует; нет конечной комбинации сумм, произведений, степеней, экспоненциальные функции, или же логарифмы будет достаточно, чтобы выразить${displaystyle x!}$; но можно найти общую формулу для факториалов, используя такие инструменты, как интегралы и пределы из исчисление. Хорошим решением этой проблемы является гамма-функция.^[1]

Существует бесконечно много непрерывных расширений факториала на нецелые числа: бесконечно много кривых можно провести через любой набор изолированных точек. Гамма-функция - наиболее полезное решение на практике, поскольку аналитический (кроме неположительных целых чисел), и его можно определить несколькими эквивалентными способами. Однако это не единственная аналитическая функция, которая расширяет факториал, добавляя к нему любую аналитическую функцию, которая равна нулю на положительных целых числах, например k грех мπИкс, даст другую функцию с этим свойством.^[1]

Гамма-функция, Γ (z) синим цветом, нанесенный вместе с Γ (z) + sin (πz) в зеленом. Обратите внимание на пересечение в положительных целых числах, оба являются действительными аналитическими продолжениями факториалов до нецелых чисел

Более ограничивающим свойством, чем удовлетворение указанной выше интерполяции, является удовлетворение отношение повторения определение переведенной версии факториальной функции,^[2][3]

${displaystyle f(1)=1,}$

${displaystyle f(x+1)=xf(x),}$

для любого положительного действительного числа Икс. Но это позволило бы произвести умножение на любую периодическую аналитическую функцию, которая дает значение 1 для положительных целых чисел, например е ^{k грех мπИкс}. Один из нескольких способов окончательно разрешить двусмысленность - это Теорема Бора – Моллерупа. В нем говорится, что при условии, что ж быть логарифмически выпуклый (или "супервыпуклый"^[4]) добавляется, он однозначно определяет ж для положительных, реальных входов. Оттуда гамма-функция может быть расширена на все действительные и комплексные значения (кроме отрицательных целых чисел и нуля) с помощью уникального аналитическое продолжение из ж.^[5]

Определение

Основное определение

Обозначение ${displaystyle Gamma (z)}$ связано с Legendre.^[1] Если действительная часть комплексного числаz положительный (${displaystyle Re (z)>0}$), то интеграл

${displaystyle Gamma (z)=int _{0}^{infty }x^{z-1}e^{-x},dx}$

сходится абсолютно, и известен как Интеграл Эйлера второго рода. (Интеграл Эйлера первого рода - это бета-функция.^[1]) С помощью интеграция по частям, видно, что:

${displaystyle {egin{aligned}Gamma (z+1)&=int _{0}^{infty }x^{z}e^{-x},dx&={Big [}-x^{z}e^{-x}{Big ]}_{0}^{infty }+int _{0}^{infty }zx^{z-1}e^{-x},dx&=lim _{x o infty }(-x^{z}e^{-x})-(-0^{z}e^{-0})+zint _{0}^{infty }x^{z-1}e^{-x},dx.end{aligned}}}$

Признавая, что ${displaystyle -x^{z}e^{-x} o 0}$ в качестве ${displaystyle x o infty ,}$

${displaystyle {egin{aligned}Gamma (z+1)&=zint _{0}^{infty }x^{z-1}e^{-x},dx&=zGamma (z).end{aligned}}}$

Мы можем рассчитать ${displaystyle Gamma (1){ ext{:}}}$

${displaystyle {egin{aligned}Gamma (1)&=int _{0}^{infty }x^{1-1}e^{-x},dx&={Big [}-e^{-x}{Big ]}_{0}^{infty }&=lim _{x o infty }(-e^{-x})-(-e^{-0})&=0-(-1)&=1.end{aligned}}}$

При условии ${displaystyle Gamma (1)=1}$ и ${displaystyle Gamma (n+1)=nGamma (n),}$

${displaystyle Gamma (n)=1cdot 2cdot 3cdots (n-1)=(n-1)!}$

для всех положительных целых чисел п. Это можно рассматривать как пример Доказательство по индукции.

Личность ${ extstyle Gamma (z)={frac {Gamma (z+1)}{z}}}$ можно использовать (или, дав тот же результат, аналитическое продолжение можно использовать), чтобы однозначно расширить интегральную формулировку для ${displaystyle Gamma (z)}$ к мероморфная функция определено для всех комплексных чисел z, кроме целых чисел, меньших или равных нулю.^[1] Именно эта расширенная версия обычно называется гамма-функцией.^[1]

Альтернативные определения

Определение Эйлера как бесконечного произведения

При стремлении приблизить ${displaystyle z!}$ для комплексного числа ${displaystyle z}$, эффективно сначала вычислить ${displaystyle n!}$ для некоторого большого целого числа ${displaystyle n}$. Используйте это, чтобы приблизить значение для ${displaystyle (n+z)!}$, а затем использовать соотношение рекурсии ${displaystyle m!=m(m-1)!}$ назад ${displaystyle n}$ раз, чтобы приблизить его к ${displaystyle z!}$. Кроме того, это приближение является точным в пределе ${displaystyle n}$ уходит в бесконечность.

В частности, для фиксированного целого числа ${displaystyle m}$, это тот случай, когда

${displaystyle lim _{n o infty }{frac {n!;(n+1)^{m}}{(n+m)!}}=1,.}$

Если ${displaystyle m}$ не является целым числом, то невозможно сказать, верно ли это уравнение, потому что мы еще не определили (в этом разделе) факториальную функцию для нецелых чисел. Однако мы действительно получаем уникальное расширение факториальной функции на нецелые числа, настаивая на том, что это уравнение продолжает выполняться, когда произвольное целое число ${displaystyle m}$ заменяется произвольным комплексным числом ${displaystyle z}$.

${displaystyle lim _{n o infty }{frac {n!;(n+1)^{z}}{(n+z)!}}=1,.}$

Умножая обе стороны на ${displaystyle z!}$ дает

${displaystyle {egin{aligned}z!&=lim _{n o infty }n!{frac {z!}{(n+z)!}}(n+1)^{z}[8pt]&=lim _{n o infty }(1cdots n){frac {1}{(1+z)cdots (n+z)}}left(left({frac {2}{1}}ight)left({frac {3}{2}}ight)cdots left({frac {n+1}{n}}ight)ight)^{z}[8pt]&=prod _{n=1}^{infty }left[{frac {1}{1+{frac {z}{n}}}}left(1+{frac {1}{n}}ight)^{z}ight].end{aligned}}}$

Этот бесконечный продукт сходится для всех комплексных чисел${displaystyle z}$ кроме отрицательных целых чисел, которые терпят неудачу из-за попытки использовать отношение рекурсии ${displaystyle m!=m(m-1)!}$ назад через значение ${displaystyle m=0}$ предполагает деление на ноль.

Аналогично для гамма-функции определение как бесконечное произведение из-за Эйлер действительно для всех комплексных чисел ${displaystyle z}$ кроме неположительных целых чисел:

${displaystyle Gamma (z)={frac {1}{z}}prod _{n=1}^{infty }{frac {left(1+{frac {1}{n}}ight)^{z}}{1+{frac {z}{n}}}},.}$

По этой конструкции гамма-функция является единственной функцией, которая одновременно удовлетворяет ${displaystyle Gamma (1)=1}$, ${displaystyle Gamma (z+1)=zGamma (z)}$ для всех комплексных чисел ${displaystyle z}$ кроме неположительных целых чисел и ${ extstyle lim _{n o infty }{frac {Gamma (n+z)}{Gamma (n);n^{z}}}=1}$ для всех комплексных чисел ${displaystyle z}$.^[1]

Определение Вейерштрасса

Определение гамма-функции из-за Weierstrass также действительно для всех комплексных чиселz кроме неположительных целых чисел:

${displaystyle Gamma (z)={frac {e^{-gamma z}}{z}}prod _{n=1}^{infty }left(1+{frac {z}{n}}ight)^{-1}e^{z/n},}$

куда ${displaystyle gamma approx 0.577216}$ это Константа Эйлера – Маскерони.^[1] Это Произведение Адамара из ${displaystyle 1/Gamma (z)}$ в переписанном виде. Действительно, поскольку ${displaystyle 1/Gamma (z)}$ является весь рода 1 с простым нулем в ${displaystyle z=0}$, у нас есть товарное представление

${displaystyle {frac {1}{Gamma (z)}}=ze^{Az+B}prod _{ho }left(1-{frac {z}{ho }}ight)e^{z/ho },}$

где произведение стоит над нулями ${displaystyle ho eq 0}$ из ${displaystyle 1/Gamma (z)}$. С ${displaystyle Gamma (z)}$ имеет простые полюсы при неположительных целых числах, отсюда следует ${displaystyle 1/Gamma (z)}$ имеет простые нули при неположительных целых числах, и поэтому приведенное выше уравнение становится формулой Вейерштрасса с ${displaystyle -Az-B}$ на месте ${displaystyle -gamma z}$. Вывод констант ${displaystyle A=gamma }$ и ${displaystyle B=0}$ является несколько техническим, но может быть достигнуто с помощью некоторых идентификаторов, включающих Дзета-функция Римана (видеть эта личность, например). См. Также Теорема факторизации Вейерштрасса.

В терминах обобщенных многочленов Лагерра

Представление неполная гамма-функция с точки зрения обобщенные полиномы Лагерра является

${displaystyle Gamma (z,x)=x^{z}e^{-x}sum _{n=0}^{infty }{frac {L_{n}^{(z)}(x)}{n+1}},}$

который сходится для ${displaystyle Re (z)>-1}$ и ${displaystyle x>0}$.^[6]

Характеристики

Общий

Другие важные функциональные уравнения для гамма-функции: Формула отражения Эйлера

${displaystyle Gamma (1-z)Gamma (z)={pi over sin(pi z)},qquad zot in mathbb {Z} }$

что подразумевает

${displaystyle Gamma (varepsilon -n)=(-1)^{n-1};{frac {Gamma (-varepsilon )Gamma (1+varepsilon )}{Gamma (n+1-varepsilon )}},}$

и Формула дублирования Лежандра

${displaystyle Gamma (z)Gamma left(z+{ frac {1}{2}}ight)=2^{1-2z};{sqrt {pi }};Gamma (2z).}$

Вывод формулы отражения Эйлера

С ${displaystyle e^{-t}=lim _{n o infty }left(1-{frac {t}{n}}ight)^{n},}$ гамма-функцию можно представить как ${displaystyle Gamma (z)=lim _{n o infty }int _{0}^{n}t^{z-1}left(1-{frac {t}{n}}ight)^{n},dt.}$ Интеграция по частям ${displaystyle n}$ раз дает ${displaystyle Gamma (z)=lim _{n o infty }{frac {n}{nz}}cdot {frac {n-1}{n(z+1)}}cdot {frac {n-2}{n(z+2)}}cdots {frac {1}{n(z+n-1)}}int _{0}^{n}t^{z+n-1},dt,}$ что равно ${displaystyle Gamma (z)=lim _{n o infty }{frac {n!}{n^{n}}}prod _{k=0}^{n}(z+k)^{-1}n^{z+n}.}$ Это можно переписать как ${displaystyle Gamma (z)=lim _{n o infty }{frac {n^{z}}{z}}prod _{k=1}^{n}{frac {k}{z+k}}=lim _{n o infty }{frac {n^{z}}{z}}prod _{k=1}^{n}{frac {1}{1+{frac {z}{k}}}}.}$ Тогда, используя функциональное уравнение гамма-функции, получаем ${displaystyle -zGamma (-z)Gamma (z)=Gamma (1-z)Gamma (z)=lim _{n o infty }{frac {1}{z}}prod _{k=1}^{n}{frac {1}{1-{frac {z^{2}}{k^{2}}}}}.}$ Может быть доказано который ${displaystyle sin(pi z)=pi zprod _{k=1}^{infty }left(1-{frac {z^{2}}{k^{2}}}ight).}$ потом ${displaystyle {frac {pi }{sin(pi z)}}=lim _{n o infty }{frac {1}{z}}prod _{k=1}^{n}{frac {1}{1-{frac {z^{2}}{k^{2}}}}}.}$ Формула отражения Эйлера следующая: ${displaystyle Gamma (1-z)Gamma (z)={frac {pi }{sin(pi z)}},qquad zot in mathbb {Z} .}$

Вывод формулы дублирования Лежандра

В бета-функция можно представить как ${displaystyle mathrm {B} (z_{1},z_{2})={frac {Gamma (z_{1})Gamma (z_{2})}{Gamma (z_{1}+z_{2})}}=int _{0}^{1}t^{z_{1}-1}(1-t)^{z_{2}-1},dt.}$ Параметр ${displaystyle z_{1}=z_{2}=z}$ дает ${displaystyle {frac {Gamma ^{2}(z)}{Gamma (2z)}}=int _{0}^{1}t^{z-1}(1-t)^{z-1},dt.}$ После замены ${displaystyle t={frac {1+x}{2}}}$ мы получили ${displaystyle {frac {Gamma ^{2}(z)}{Gamma (2z)}}={frac {1}{2^{2z-1}}}int _{-1}^{1}left(1-x^{2}ight)^{z-1},dx.}$ Функция ${displaystyle (1-x^{2})^{z-1}}$ четно, следовательно ${displaystyle 2^{2z-1}Gamma ^{2}(z)=2Gamma (2z)int _{0}^{1}(1-x^{2})^{z-1},dx.}$ Теперь предположим ${displaystyle mathrm {B} left({frac {1}{2}},zight)=int _{0}^{1}t^{{frac {1}{2}}-1}(1-t)^{z-1},dt,quad t=s^{2}.}$ потом ${displaystyle mathrm {B} left({frac {1}{2}},zight)=2int _{0}^{1}(1-s^{2})^{z-1},ds=2int _{0}^{1}(1-x^{2})^{z-1},dx.}$ Из этого следует ${displaystyle 2^{2z-1}Gamma ^{2}(z)=Gamma (2z)mathrm {B} left({frac {1}{2}},zight).}$ С ${displaystyle mathrm {B} left({frac {1}{2}},zight)={frac {Gamma left({frac {1}{2}}ight)Gamma (z)}{Gamma left(z+{frac {1}{2}}ight)}},quad Gamma left({frac {1}{2}}ight)={sqrt {pi }},}$ формула дублирования Лежандра: ${displaystyle Gamma (z)Gamma left(z+{frac {1}{2}}ight)=2^{1-2z}{sqrt {pi }};Gamma (2z).}$

Формула дублирования - это частный случай теорема умножения (Видеть,^[6] Уравнение 5.5.6)

${displaystyle prod _{k=0}^{m-1}Gamma left(z+{frac {k}{m}}ight)=(2pi )^{frac {m-1}{2}};m^{{frac {1}{2}}-mz};Gamma (mz).}$

Простое, но полезное свойство, которое можно увидеть из определения предела, это:

${displaystyle {overline {Gamma (z)}}=Gamma ({overline {z}});Rightarrow ;Gamma (z)Gamma ({overline {z}})in mathbb {R} .}$

В частности, с z = а + би, этот продукт

${displaystyle |Gamma (a+bi)|^{2}=|Gamma (a)|^{2}prod _{k=0}^{infty }{frac {1}{1+{frac {b^{2}}{(a+k)^{2}}}}}}$

Если действительная часть является целым или полуцелым числом, это может быть конечно выражено в закрытая форма:

${displaystyle {egin{aligned}|Gamma (bi)|^{2}&={frac {pi }{bsinh(pi b)}}[6pt]|Gamma left({ frac {1}{2}}+biight)|^{2}&={frac {pi }{cosh(pi b)}}|Gamma left(1+biight)|^{2}&={frac {pi b}{sinh(pi b)}}|Gamma left(1+n+biight)|^{2}&={frac {pi b}{sinh(pi b)}}prod _{k=1}^{n}left(k^{2}+b^{2}ight),quad nin mathbb {N} |Gamma left(-n+biight)|^{2}&={frac {pi }{bsinh(pi b)}}prod _{k=1}^{n}left(k^{2}+b^{2}ight)^{-1},quad nin mathbb {N} |Gamma left({ frac {1}{2}}pm n+biight)|^{2}&={frac {pi }{cosh(pi b)}}prod _{k=1}^{n}left(left(k-{ frac {1}{2}}ight)^{2}+b^{2}ight)^{pm 1},quad nin mathbb {N} end{aligned}}}$

Доказательство формул для целой или полуцелой действительной части

Сначала рассмотрим формулу отражения, примененную к ${displaystyle z=bi}$. ${displaystyle Gamma (bi)Gamma (1-bi)={frac {pi }{sin(pi bi)}}}$ Применяя рекуррентное соотношение ко второму слагаемому, имеем ${displaystyle -bicdot Gamma (bi)Gamma (-bi)={frac {pi }{sin(pi bi)}}}$ что при простой перестановке дает ${displaystyle Gamma (bi)Gamma (-bi)={frac {pi }{-bisin(pi bi)}}={frac {pi }{bsinh(pi b)}}}$ Во-вторых, рассмотрим формулу отражения, примененную к ${displaystyle z={ frac {1}{2}}+bi}$. ${displaystyle Gamma ({ frac {1}{2}}+bi)Gamma left(1-({ frac {1}{2}}+bi)ight)=Gamma ({ frac {1}{2}}+bi)Gamma ({ frac {1}{2}}-bi)={frac {pi }{sin left(pi ({ frac {1}{2}}+bi)ight)}}={frac {pi }{cos(pi bi)}}={frac {pi }{cosh(pi b)}}}$ Формулы для других значений ${displaystyle z}$ для которых действительная часть является целым или полуцелым числом, за которым быстро следует индукция используя рекуррентное соотношение в положительном и отрицательном направлениях.

Возможно, наиболее известным значением гамма-функции при нецелочисленном аргументе является

${displaystyle Gamma left({ frac {1}{2}}ight)={sqrt {pi }},}$

который можно найти, установив ${ extstyle z={frac {1}{2}}}$ в формулах отражения или дублирования, используя отношение к бета-функция приведенный ниже с ${ extstyle x=y={frac {1}{2}}}$, или просто сделав замену ${displaystyle u={sqrt {x}}}$ в интегральном определении гамма-функции, в результате чего Гауссов интеграл. В общем, для неотрицательных целых значений ${displaystyle n}$ у нас есть:

${displaystyle {egin{aligned}Gamma left({ frac {1}{2}}+night)&={(2n)! over 4^{n}n!}{sqrt {pi }}={frac {(2n-1)!!}{2^{n}}}{sqrt {pi }}={inom {n-{frac {1}{2}}}{n}}n!{sqrt {pi }}[8pt]Gamma left({ frac {1}{2}}-night)&={(-4)^{n}n! over (2n)!}{sqrt {pi }}={frac {(-2)^{n}}{(2n-1)!!}}{sqrt {pi }}={frac {sqrt {pi }}{{inom {-1/2}{n}}n!}}end{aligned}}}$

куда ${displaystyle n!!}$ обозначает двойной факториал из п и когда ${displaystyle n=0}$, ${displaystyle n!!=1}$. Видеть Частные значения гамма-функции для расчетных значений.

Может возникнуть соблазн обобщить результат, что ${ extstyle Gamma left({frac {1}{2}}ight)={sqrt {pi }}}$ путем поиска формулы для других индивидуальных значений ${displaystyle Gamma (r)}$ куда ${displaystyle r}$ рационально, тем более что согласно Теорема Гаусса о дигамме, это возможно для тесно связанных функция дигаммы при каждом рациональном значении. Однако эти цифры ${displaystyle Gamma (r)}$ как известно, не могут быть выражены сами по себе в терминах элементарных функций. Доказано, что ${displaystyle Gamma (n+r)}$ это трансцендентное число и алгебраически независимый из ${displaystyle pi }$ для любого целого ${displaystyle n}$ и каждая из фракций ${ extstyle r={frac {1}{6}},{frac {1}{4}},{frac {1}{3}},{frac {2}{3}},{frac {3}{4}},{frac {5}{6}}}$.^[7] В общем, при вычислении значений гамма-функции мы должны ограничиваться численными приближениями.

Еще один полезный предел для асимптотических приближений:

${displaystyle lim _{n o infty }{frac {Gamma (n+alpha )}{Gamma (n)n^{alpha }}}=1,qquad alpha in mathbb {C} .}$

Производные гамма-функции описываются в терминах полигамма функция. Например:

${displaystyle Gamma '(z)=Gamma (z)psi _{0}(z).}$

Для положительного целого числам производная гамма-функции может быть вычислена следующим образом (здесь${displaystyle gamma }$ это Константа Эйлера – Маскерони ):

${displaystyle Gamma '(m+1)=m!left(-gamma +sum _{k=1}^{m}{frac {1}{k}}ight),.}$

За ${displaystyle Re (x)>0}$ то ${displaystyle n}$-я производная гамма-функции:

Производная функции Γ (z)

${displaystyle {frac {d^{n}}{dx^{n}}}Gamma (x)=int _{0}^{infty }t^{x-1}e^{-t}(ln t)^{n},dt.}$

(Это может быть получено путем дифференцирования интегральной формы гамма-функции по ${displaystyle x}$, и используя технику дифференцирование под знаком интеграла.)

Используя личность

${displaystyle Gamma ^{(n)}(1)=(-1)^{n}n!sum limits _{pi ,vdash ,n},prod _{i=1}^{r}{frac {zeta ^{*}(a_{i})}{k_{i}!cdot a_{i}}}qquad zeta ^{*}(x):={egin{cases}zeta (x)&xeq 1gamma &x=1end{cases}}}$

куда ${displaystyle zeta (z)}$ это Дзета-функция Римана, и ${displaystyle pi }$ это раздел из ${displaystyle n}$ данный

${displaystyle pi =underbrace {a_{1}+cdots +a_{1}} _{k_{1}{ ext{ terms}}}+cdots +underbrace {a_{r}+cdots +a_{r}} _{k_{r}{ ext{ terms}}},}$

у нас в частности

${displaystyle Gamma (z)={frac {1}{z}}-gamma +{ frac {1}{2}}left(gamma ^{2}+{frac {pi ^{2}}{6}}ight)z-{ frac {1}{6}}left(gamma ^{3}+{frac {gamma pi ^{2}}{2}}+2zeta (3)ight)z^{2}+O(z^{3}).}$

Неравенства

При ограничении положительными действительными числами гамма-функция является строго логарифмически выпуклая функция. Это свойство может быть указано любым из следующих трех эквивалентных способов:

• Для любых двух положительных действительных чисел ${displaystyle x_{1}}$ и ${displaystyle x_{2}}$, и для любого ${displaystyle tin [0,1]}$,

${displaystyle Gamma (tx_{1}+(1-t)x_{2})leq Gamma (x_{1})^{t}Gamma (x_{2})^{1-t}.}$

• Для любых двух положительных действительных чисел Икс и у с у > Икс,

${displaystyle left({frac {Gamma (y)}{Gamma (x)}}ight)^{frac {1}{y-x}}>exp left({frac {Gamma '(x)}{Gamma (x)}}ight).}$

• Для любого положительного действительного числа ${displaystyle x}$,

${displaystyle Gamma ''(x)Gamma (x)>Gamma '(x)^{2}.}$

Последнее из этих утверждений, по сути, по определению совпадает с утверждением, что ${displaystyle psi ^{(1)}(x)>0}$, куда ${displaystyle psi ^{(1)}}$ это полигамма функция порядка 1. Чтобы доказать логарифмическую выпуклость гамма-функции, достаточно заметить, что ${displaystyle psi ^{(1)}}$ имеет представление серии, которое для положительных вещественных Икс, состоит только из положительных терминов.

Логарифмическая выпуклость и Неравенство Дженсена вместе означают, что для любых положительных действительных чисел ${displaystyle x_{1},ldots ,x_{n}}$ и ${displaystyle a_{1},ldots ,a_{n}}$,

${displaystyle Gamma left({frac {a_{1}x_{1}+cdots +a_{n}x_{n}}{a_{1}+cdots +a_{n}}}ight)leq {igl (}Gamma (x_{1})^{a_{1}}cdots Gamma (x_{n})^{a_{n}}{igr )}^{frac {1}{a_{1}+cdots +a_{n}}}.}$

Также существуют ограничения на отношения гамма-функций. Самый известный из них Неравенство Гаучи, который говорит, что для любого положительного действительного числа Икс и любой s ∈ (0, 1),

${displaystyle x^{1-s}<{frac {Gamma (x+1)}{Gamma (x+s)}}<(x+1)^{1-s}.}$

Формула Стирлинга

Представление гамма-функции в комплексной плоскости. Каждая точка ${displaystyle z}$ раскрашен согласно аргументу ${displaystyle Gamma (z)}$. Контурная диаграмма модуля ${displaystyle |Gamma (z)|}$ также отображается.

Трехмерный график абсолютного значения комплексной гамма-функции

Поведение ${displaystyle Gamma (z)}$ для возрастающей положительной переменной просто. Он растет быстро, быстрее, чем экспоненциальная функция на самом деле. Асимптотически при ${ extstyle z o infty ,}$ величина гамма-функции определяется выражением Формула Стирлинга

${displaystyle Gamma (z+1)sim {sqrt {2pi z}}left({frac {z}{e}}ight)^{z},}$

где символ ${displaystyle sim }$ влечет асимптотическую сходимость. Другими словами, отношение двух сторон сходится к 1 как ${ extstyle z o +infty }$ .^[1]

Остатки

Поведение для неположительных ${displaystyle z}$ более сложный. Интеграл Эйлера не сходится при ${displaystyle zleq 0}$, но функция, которую он определяет в положительной комплексной полуплоскости, имеет единственное аналитическое продолжение в отрицательную полуплоскость. Один из способов найти это аналитическое продолжение - использовать интеграл Эйлера для положительных аргументов и расширить область до отрицательных чисел путем повторного применения рекуррентной формулы,^[1]

${displaystyle Gamma (z)={frac {Gamma (z+n+1)}{z(z+1)cdots (z+n)}},}$

выбор ${displaystyle n}$ такой, что ${displaystyle z+n}$ положительный. Произведение в знаменателе равно нулю, когда ${displaystyle z}$ равно любому из целых чисел ${displaystyle 0,-1,-2,cdots }$. Таким образом, гамма-функция должна быть неопределенной в этих точках, чтобы избежать деление на ноль; это мероморфная функция с простые столбы при неположительных целых числах.^[1]

Для функции ${displaystyle f}$ комплексной переменной ${displaystyle z}$, в простой полюс ${displaystyle c}$, то остаток из ${displaystyle f}$ дан кем-то:

${displaystyle operatorname {Res} (f,c)=lim _{z o c}(z-c)f(z).}$

Для простого полюса ${displaystyle z=-n,}$ перепишем формулу рекуррентности как:

${displaystyle (z+n)Gamma (z)={frac {Gamma (z+n+1)}{z(z+1)cdots (z+n-1)}}.}$

Числитель при ${displaystyle z=-n,}$ является

${displaystyle Gamma (z+n+1)=Gamma (1)=1}$

и знаменатель

${displaystyle z(z+1)cdots (z+n-1)=-n(1-n)cdots (n-1-n)=(-1)^{n}n!.}$

Таким образом, остатки гамма-функции в этих точках равны:

${displaystyle operatorname {Res} (Gamma ,-n)={frac {(-1)^{n}}{n!}}.}$^[8]

Гамма-функция не равна нулю всюду вдоль вещественной линии, хотя она сколь угодно близка к нулю при z → −∞. На самом деле нет никакого комплексного числа ${displaystyle z}$ для которого ${displaystyle Gamma (z)=0}$, и, следовательно, обратная гамма-функция ${ extstyle {frac {1}{Gamma (z)}}}$ является вся функция, с нулями на ${displaystyle z=0,-1,-2,cdots }$.^[1]

Минимумы

Гамма-функция имеет локальный минимум при z_мин ≈ +1.46163214496836234126 (усечено), где достигает значения Γ (z_мин) ≈ +0.88560319441088870027 (усечено). Гамма-функция должна менять знак между полюсами, потому что произведение в прямом повторении содержит нечетное количество отрицательных факторов, если количество полюсов между ${displaystyle z}$ и ${displaystyle z+n}$ является нечетным и четным числом, если число полюсов четное.^[8]

Интегральные представления

Помимо интеграла Эйлера второго рода существует множество формул, выражающих гамма-функцию как интеграл. Например, когда реальная часть z положительный,^[9]

${displaystyle Gamma (z)=int _{0}^{1}left(log {frac {1}{t}}ight)^{z-1},dt.}$

Первая интегральная формула Бине для гамма-функции утверждает, что когда действительная часть z положительно, то:^[10]

${displaystyle log Gamma (z)=left(z-{frac {1}{2}}ight)log z-z+{frac {1}{2}}log(2pi )+int _{0}^{infty }left({frac {1}{2}}-{frac {1}{t}}+{frac {1}{e^{t}-1}}ight){frac {e^{-tz}}{t}},dt.}$

Интеграл в правой части можно интерпретировать как Преобразование Лапласа. То есть,

${displaystyle log left(Gamma (z)left({frac {e}{z}}ight)^{z}{sqrt {2pi z}}ight)={mathcal {L}}left({frac {1}{2t}}-{frac {1}{t^{2}}}+{frac {1}{t(e^{t}-1)}}ight)(z).}$

Вторая интегральная формула Бине утверждает, что снова, когда действительная часть z положительно, то:^[11]

${displaystyle log Gamma (z)=left(z-{frac {1}{2}}ight)log z-z+{frac {1}{2}}log(2pi )+2int _{0}^{infty }{frac {arctan(t/z)}{e^{2pi t}-1}},dt.}$

Позволять C быть Контур Ганкеля, то есть путь, который начинается и заканчивается в точке ∞ на Сфера Римана, единичный касательный вектор которого сходится к −1 в начале пути и до 1 в конце, который имеет номер намотки 1 вокруг 0, и который не пересекает [0, ∞). Исправить ветку ${displaystyle log(-t)}$ взяв срезанную ветку [0, ∞) и взяв ${displaystyle log(-t)}$ быть реальным, когда т находится на отрицательной действительной оси. Предполагать z не является целым числом. Тогда формула Ганкеля для гамма-функции:^[12]

${displaystyle Gamma (z)=-{frac {1}{2isin pi z}}int _{C}(-t)^{z-1}e^{-t},dt,}$

куда ${displaystyle (-t)^{z-1}}$ интерпретируется как ${displaystyle exp((z-1)log(-t))}$. Формула отражения приводит к тесно связанному выражению

${displaystyle {frac {1}{Gamma (z)}}={frac {i}{2pi }}int _{C}(-t)^{-z}e^{-t},dt,}$

снова действует всякий раз, когда z не является целым числом.

Разложение в ряд Фурье

В логарифм гамма-функции имеет следующие Ряд Фурье расширение для ${displaystyle 0<z<1:}$

${displaystyle ln Gamma (z)=left({frac {1}{2}}-zight)(gamma +ln 2)+(1-z)ln pi -{frac {1}{2}}ln sin(pi z)+{frac {1}{pi }}sum _{n=1}^{infty }{frac {ln n}{n}}sin(2pi nz),}$

которое долгое время приписывали Эрнст Куммер, выведший его в 1847 году.^[13][14] Тем не мение, Ярослав Благушин обнаружил, что Карл Йохан Мальмстен Впервые эта серия была выведена в 1842 году.^[15][16]

Формула Раабе

В 1840 г. Йозеф Людвиг Раабе доказал, что

${displaystyle int _{a}^{a+1}ln Gamma (z),dz={ frac {1}{2}}ln 2pi +aln a-a,quad a>0.}$

В частности, если ${displaystyle a=0}$ тогда

${displaystyle int _{0}^{1}ln Gamma (z),dz={ frac {1}{2}}ln 2pi .}$

Последнее может быть получено путем логарифмирования в приведенной выше формуле умножения, которая дает выражение для суммы Римана подынтегральной функции. Принимая предел для ${displaystyle aightarrow infty }$ дает формулу.

Функция Пи

Альтернативное обозначение, которое первоначально было введено Гаусс и который иногда использовался, это ${displaystyle Pi }$-функция, которая в терминах гамма-функции есть

${displaystyle Pi (z)=Gamma (z+1)=zGamma (z)=int _{0}^{infty }e^{-t}t^{z},dt,}$

так что ${displaystyle Pi (n)=n!}$ для каждого неотрицательного целого числа ${displaystyle n}$.

Используя функцию пи, формула отражения принимает вид

${displaystyle Pi (z)Pi (-z)={frac {pi z}{sin(pi z)}}={frac {1}{operatorname {sinc} (z)}}}$

куда грех нормализованный функция sinc, а теорема умножения принимает вид

${displaystyle Pi left({frac {z}{m}}ight),Pi left({frac {z-1}{m}}ight)cdots Pi left({frac {z-m+1}{m}}ight)=(2pi )^{frac {m-1}{2}}m^{-z-{frac {1}{2}}}Pi (z) .}$

Мы также иногда находим

${displaystyle pi (z)={frac {1}{Pi (z)}} ,}$

который является вся функция, определенный для каждого комплексного числа, как и обратная гамма-функция. Который ${displaystyle pi (z)}$ целиком в нем нет полюсов, поэтому ${displaystyle Pi left(zight)}$, подобно ${displaystyle Gamma left(zight)}$, не имеет нули.

В объем п-эллипсоид с радиусами р₁, ..., р_п можно выразить как

${displaystyle V_{n}(r_{1},dotsc ,r_{n})={frac {pi ^{frac {n}{2}}}{Pi left({frac {n}{2}}ight)}}prod _{k=1}^{n}r_{k}.}$

Отношение к другим функциям

• В первом интеграле выше, который определяет гамма-функцию, пределы интегрирования фиксированы. Верхний и нижний неполные гамма-функции являются функциями, полученными путем изменения нижнего или верхнего (соответственно) предела интегрирования.
• Гамма-функция связана с бета-функция по формуле

${displaystyle mathrm {B} (x,y)=int _{0}^{1}t^{x-1}(1-t)^{y-1},dt={frac {Gamma (x),Gamma (y)}{Gamma (x+y)}}.}$

• В логарифмическая производная гамма-функции называется функция дигаммы; высшие производные полигамма-функции.
• Аналог гамма-функции над конечное поле или конечное кольцо это Гауссовы суммы, тип экспоненциальная сумма.
• В обратная гамма-функция является вся функция и изучалась как конкретная тема.
• Гамма-функция также играет важную роль в Дзета-функция Римана, ${displaystyle zeta (z)}$.

${displaystyle pi ^{-{frac {z}{2}}};Gamma left({frac {z}{2}}ight)zeta (z)=pi ^{-{frac {1-z}{2}}};Gamma left({frac {1-z}{2}}ight);zeta (1-z).}$

Он также появляется в следующей формуле:

${displaystyle zeta (z)Gamma (z)=int _{0}^{infty }{frac {u^{z}}{e^{u}-1}},{frac {du}{u}},}$

что действительно только для ${displaystyle Re (z)>1}$.

Логарифм гамма-функции удовлетворяет следующей формуле Лерха:

${displaystyle log Gamma (x)=zeta _{H}'(0,x)-zeta '(0),}$

куда ${displaystyle zeta _{H}}$ это Дзета-функция Гурвица, ${displaystyle zeta }$ - дзета-функция Римана, а простое число (′) обозначает дифференцирование по первой переменной.

• Гамма-функция связана с растянутая экспоненциальная функция. Например, моменты этой функции равны

${displaystyle langle au ^{n}angle equiv int _{0}^{infty }dt,t^{n-1},e^{-left({frac {t}{ au }}ight)^{eta }}={frac { au ^{n}}{eta }}Gamma left({n over eta }ight).}$

Особые ценности

Основная статья: Частные значения гамма-функции

Включая до первых 20 цифр после десятичной точки, некоторые конкретные значения гамма-функции:

${displaystyle {egin{array}{rcccl}Gamma left(-{ frac {3}{2}}ight)&=&{ frac {4}{3}}{sqrt {pi }}&approx &+2.36327,18012,07354,70306Gamma left(-{ frac {1}{2}}ight)&=&-2{sqrt {pi }}&approx &-3.54490,77018,11032,05459Gamma left({ frac {1}{2}}ight)&=&{sqrt {pi }}&approx &+1.77245,38509,05516,02729Gamma (1)&=&0!&=&+1Gamma left({ frac {3}{2}}ight)&=&{ frac {1}{2}}{sqrt {pi }}&approx &+0.88622,69254,52758,01364Gamma (2)&=&1!&=&+1Gamma left({ frac {5}{2}}ight)&=&{ frac {3}{4}}{sqrt {pi }}&approx &+1.32934,03881,79137,02047Gamma (3)&=&2!&=&+2Gamma left({ frac {7}{2}}ight)&=&{ frac {15}{8}}{sqrt {pi }}&approx &+3.32335,09704,47842,55118Gamma (4)&=&3!&=&+6end{array}}}$

Комплексная гамма-функция не определена для неположительных целых чисел, но в этих случаях значение может быть определено в Сфера Римана в качестве ∞. В обратная гамма-функция является хорошо определенный и аналитический при этих значениях (и в вся комплексная плоскость ):

${displaystyle {frac {1}{Gamma (-3)}}={frac {1}{Gamma (-2)}}={frac {1}{Gamma (-1)}}={frac {1}{Gamma (0)}}=0.}$

Лог-гамма-функция

Аналитическая функция журнал Γ (z)

Поскольку гамма- и факторные функции растут так быстро для умеренно больших аргументов, многие вычислительные среды включают функцию, которая возвращает натуральный логарифм гамма-функции (часто называют lgamma или же lngamma в среде программирования или гаммалн в электронных таблицах); это растет намного медленнее, и для комбинаторных вычислений позволяет складывать и вычитать журналы вместо умножения и деления очень больших значений. Его часто определяют как^[17]

${displaystyle ln Gamma (z)=-gamma z-ln z+sum _{k=1}^{infty }left[{frac {z}{k}}-ln left(1+{frac {z}{k}}ight)ight].}$

В функция дигаммы, которая является производной от этой функции, также часто встречается в контексте технических и физических приложений, например с распространением волн функциональное уравнение

${displaystyle ln Gamma (z)=ln Gamma (z+1)-ln z}$

часто используется, так как позволяет определять значения функции в одной полосе шириной 1 дюйм z с соседней полосы. В частности, начиная с хорошего приближения дляz с большой реальной частью можно шаг за шагом идти к желаемомуz. После указания Карл Фридрих Гаусс, Rocktaeschel (1922) предложил для ${displaystyle ln(Gamma (z))}$ приближение для больших Re (z):

${displaystyle ln Gamma (z)approx (z-{ frac {1}{2}})ln z-z+{ frac {1}{2}}ln(2pi ).}$

Это можно использовать для точного приближения ln (Γ (z)) за z с меньшим Re (z) через (П. Э. Бёмер, 1939)

${displaystyle ln Gamma (z-m)=ln Gamma (z)-sum _{k=1}^{m}ln(z-k).}$

Более точное приближение можно получить, используя больше членов из асимптотических разложений ln (Γ (z)) и Γ (z), основанные на приближении Стирлинга.

${displaystyle Gamma (z)sim z^{z-{frac {1}{2}}}e^{-z}{sqrt {2pi }}left(1+{frac {1}{12z}}+{frac {1}{288z^{2}}}-{frac {139}{51,840z^{3}}}-{frac {571}{2,488,320z^{4}}}ight)}$

в качестве |z| → ∞ при постоянном |аргумент (z)| <π.

В более «естественном» изложении:

${displaystyle ln Gamma (z)sim zln(z)-z-{ frac {1}{2}}ln left({frac {z}{2pi }}ight)+{frac {1}{12z}}-{frac {1}{360z^{3}}}+{frac {1}{1260z^{5}}}}$

в качестве |z| → ∞ при постоянном |аргумент (z)| <π.

Коэффициенты при членах k > 1 из z^{−k + 1} в последнем расширении просто

${displaystyle {frac {B_{k}}{k(k-1)}}}$

где B_k являются Числа Бернулли.

Характеристики

В Теорема Бора – Моллерупа утверждает, что среди всех функций, расширяющих факториальные функции до положительных действительных чисел, только гамма-функция является бревенчато-выпуклый, то есть его натуральный логарифм является выпуклый на положительной действительной оси. Другая характеристика дается Теорема Виландта.

В определенном смысле ln (Γ) функция - более естественная форма; это делает некоторые внутренние атрибуты функции более понятными. Ярким примером является Серия Тейлор из ln (Γ) около 1:

${displaystyle ln Gamma (z+1)=-gamma z+sum _{k=2}^{infty }{frac {zeta (k)}{k}},(-z)^{k}qquad forall ;|z|<1}$

с ζ(k) обозначая Дзета-функция Римана в k.

Итак, используя следующее свойство:

${displaystyle zeta (s)Gamma (s)=int _{0}^{infty }{frac {t^{s}}{e^{t}-1}},{frac {dt}{t}}}$

мы можем найти интегральное представление для ln (Γ) функция:

${displaystyle ln Gamma (z+1)=-gamma z+int _{0}^{infty }{frac {,left(e^{-zt}-1+ztight),}{tleft(e^{t}-1ight)}},dt}$

или, установив z = 1 получить интеграл для γ, мы можем заменить γ член с его интегралом и включите его в формулу выше, чтобы получить:

${displaystyle ln Gamma (z+1)=int _{0}^{infty }{frac {,left(e^{-zt}-ze^{-t}-1+zight),}{t(e^{t}-1)}},dt,.}$

Также существуют специальные формулы для логарифма гамма-функции для рациональных z. Например, если ${displaystyle k}$ и ${displaystyle n}$ целые числа с ${displaystyle k<n}$ и ${displaystyle keq n/2,,}$ тогда

${displaystyle {egin{aligned}ln Gamma {iggl (}!{frac {k}{n}}!{iggr )}={}&{frac {,(n-2k)ln 2pi ,}{2n}}+{frac {1}{2}}left{,ln pi -ln sin {frac {pi k}{n}},ight}+{frac {1}{pi }}!sum _{r=1}^{n-1}{frac {,gamma +ln r,}{r}}cdot sin {frac {,2pi rk,}{n}}&{}-{frac {1}{2pi }}sin {frac {2pi k}{n}}cdot !int _{0}^{infty }!!{frac {,e^{-nx}!cdot ln x,}{,cosh x-cos(2pi k/n),}},{mathrm {d} }xend{aligned}}}$

видеть.^[18]Эта формула иногда используется для численных расчетов, поскольку подынтегральное выражение уменьшается очень быстро.

Интеграция по логарифмической гамме

Интегральный

${displaystyle int _{0}^{z}ln Gamma (x),dx}$

можно выразить через Barnes грамм-функция^[19][20] (видеть Barnes грамм-функция для доказательства):

${displaystyle int _{0}^{z}ln Gamma (x),dx={frac {z}{2}}ln(2pi )+{frac {z(1-z)}{2}}+zln Gamma (z)-ln G(z+1)}$

куда Re (z) > −1.

Его также можно записать в терминах Дзета-функция Гурвица:^[21][22]

${displaystyle int _{0}^{z}ln Gamma (x),dx={frac {z}{2}}ln(2pi )+{frac {z(1-z)}{2}}-zeta '(-1)+zeta '(-1,z).}$

Когда ${displaystyle z=1}$ следует, что

${displaystyle int _{0}^{1}ln Gamma (x),dx={frac {1}{2}}log(2pi ),}$

и это следствие Формула Раабе также. О. Эспиноза и В. Молл вывели аналогичную формулу для интеграла квадрата ${displaystyle log Gamma }$:^[23]

${displaystyle int _{0}^{1}log ^{2}Gamma (x)dx={frac {gamma ^{2}}{12}}+{frac {pi ^{2}}{48}}+{frac {1}{3}}gamma L_{1}+{frac {4}{3}}L_{1}^{2}-left(gamma +2L_{1}ight){frac {zeta ^{prime }(2)}{pi ^{2}}}+{frac {zeta ^{prime prime }(2)}{2pi ^{2}}},}$

куда ${displaystyle L_{1}}$ является ${displaystyle {frac {1}{2}}log(2pi )}$.

Д. Х. Бейли и его соавторы^[24] дал оценку

${displaystyle L_{n}:=int _{0}^{1}log ^{n}Gamma (x)dx}$

когда ${displaystyle n=1,2}$ в терминах дзета-функции Торнхейма-Виттена и ее производных.

Кроме того, также известно, что^[25]

${displaystyle lim _{n o infty }{frac {L_{n}}{n!}}=1.}$

Приближения

Гамма сравнения (синяя линия) с факториалом (синие точки) и приближением Стирлинга (красная линия)

Комплексные значения гамма-функции могут быть вычислены численно с произвольной точностью, используя Приближение Стирлинга или Приближение Ланцоша.

Гамма-функцию можно вычислить с фиксированной точностью для ${displaystyle operatorname {Re} (z)in [1,2]}$ применяя интеграция по частям к интегралу Эйлера. Для любого положительного числаИкс гамма-функцию можно записать

${displaystyle {egin{aligned}Gamma (z)&=int _{0}^{x}e^{-t}t^{z},{frac {dt}{t}}+int _{x}^{infty }e^{-t}t^{z},{frac {dt}{t}}&=x^{z}e^{-x}sum _{n=0}^{infty }{frac {x^{n}}{z(z+1)cdots (z+n)}}+int _{x}^{infty }e^{-t}t^{z},{frac {dt}{t}}.end{aligned}}}$

Когда Re (z) ∈ [1,2] и ${displaystyle xgeq 1}$, модуль последнего интеграла меньше, чем ${displaystyle (x+1)e^{-x}}$. Выбрав достаточно большой ${displaystyle x}$, последнее выражение можно сделать меньше, чем ${displaystyle 2^{-N}}$ для любого желаемого значения${displaystyle N}$. Таким образом, гамма-функцию можно оценить как ${displaystyle N}$ бит точности с вышеуказанной серией.

Быстрый алгоритм вычисления гамма-функции Эйлера для любого алгебраического аргумента (в том числе рационального) был построен Е.А. Карацуба,^[26][27][28]

Для аргументов, кратных целому числу 1/24, гамма-функцию также можно быстро оценить с помощью среднее арифметико-геометрическое итерации (см. частные значения гамма-функции и Борвейн и Цукер (1992) Ошибка harvtxt: цель отсутствует: CITEREFBorweinZucker1992 (помощь)).

Приложения

Один автор описывает гамма-функцию как «возможно, наиболее распространенную специальную функцию или наименее« особую »из них. Другие трансцендентные функции […] называются« особенными », потому что вы, вероятно, можете избежать некоторых из них, избегая многих из них. специализированные математические разделы. С другой стороны, гамма-функция у = Γ (Икс) избежать труднее всего ».^[29]

Проблемы интеграции

Гамма-функция находит применение в таких разнообразных областях, как квантовая физика, астрофизика и динамика жидкостей.^[30] В гамма-распределение, который формулируется в терминах гамма-функции, используется в статистика моделировать широкий спектр процессов; например, время между возникновением землетрясений.^[31]

Основная причина полезности гамма-функции в таких контекстах - преобладание выражений типа ${displaystyle f(t)e^{-g(t)}}$ которые описывают процессы, экспоненциально затухающие во времени или пространстве. Интегралы таких выражений иногда могут быть решены в терминах гамма-функции, когда элементарного решения не существует. Например, если ж является степенной функцией и грамм является линейной функцией, простая замена переменных дает оценку

${displaystyle int _{0}^{infty }t^{b}e^{-at},dt={frac {Gamma (b+1)}{a^{b+1}}}.}$

Тот факт, что интегрирование выполняется по всей положительной действительной линии, может означать, что гамма-функция описывает кумуляцию зависящего от времени процесса, который продолжается бесконечно, или значение может быть суммой распределения в бесконечном пространстве.

Конечно, часто бывает полезно использовать пределы интеграции, отличные от 0 и ∞ для описания кумуляции конечного процесса, и в этом случае обычная гамма-функция больше не является решением; тогда решение называется неполная гамма-функция. (Обычная гамма-функция, полученная интегрированием по всей положительной действительной прямой, иногда называется полная гамма-функция для контраста.)

Важной категорией экспоненциально убывающих функций является категория Гауссовы функции

${displaystyle ae^{-{frac {(x-b)^{2}}{c^{2}}}}}$

и их интегралы, такие как функция ошибки. Между этими функциями и гамма-функцией существует множество взаимосвязей; в частности, фактор ${displaystyle {sqrt {pi }}}$ полученный путем оценки ${ extstyle Gamma left({frac {1}{2}}ight)}$ "то же самое", что и в нормирующем множителе функции ошибок и нормальное распределение.

Интегралы, которые мы обсуждали до сих пор, включают трансцендентные функции, но гамма-функция также возникает из интегралов от чисто алгебраических функций. В частности, длина дуги из эллипсы и из лемниската, которые являются кривыми, определяемыми алгебраическими уравнениями, задаются формулами эллиптические интегралы что в особых случаях может быть оценено с помощью гамма-функции. Гамма-функцию также можно использовать для рассчитать «объем» и «площадь» из п-размерный гиперсферы.

Расчет продуктов

Способность гамма-функции обобщать факторные произведения немедленно приводит к приложениям во многих областях математики; в комбинаторика, а также в таких областях, как теория вероятности и расчет степенной ряд. Многие выражения, включающие произведения следующих друг за другом целых чисел, могут быть записаны как некоторая комбинация факториалов, наиболее важным примером, возможно, является выражение биномиальный коэффициент

${displaystyle {inom {n}{k}}={frac {n!}{k!(n-k)!}}.}$

Пример биномиальных коэффициентов объясняет, почему свойства гамма-функции при расширении на отрицательные числа являются естественными. Биномиальный коэффициент дает количество способов выбора k элементы из набора п элементы; если k > п, способов конечно нет. Если k > п, (п − k)! является факториалом отрицательного целого числа и, следовательно, бесконечным, если мы используем определение факториалов гамма-функцией - деление на бесконечность дает ожидаемое значение 0.

Мы можем заменить факториал на гамма-функцию, чтобы распространить любую такую ​​формулу на комплексные числа. Как правило, это работает для любого продукта, в котором каждый фактор является рациональная функция индексной переменной путем разложения рациональной функции на линейные выражения. Если п и Q являются моническими многочленами степени м и п с соответствующими корнями п₁, …, п_м и q₁, …, q_п, у нас есть

${displaystyle prod _{i=a}^{b}{frac {P(i)}{Q(i)}}=left(prod _{j=1}^{m}{frac {Gamma (b-p_{j}+1)}{Gamma (a-p_{j})}}ight)left(prod _{k=1}^{n}{frac {Gamma (a-q_{k})}{Gamma (b-q_{k}+1)}}ight).}$

Если у нас есть способ численно рассчитать гамма-функцию, то вычислить числовые значения таких продуктов несложно. Количество гамма-функций в правой части зависит только от степени полиномов, поэтому не имеет значения, б − а равно 5 или 10⁵. Принимая соответствующие ограничения, уравнение также может выполняться, даже когда левое произведение содержит нули или полюсы.

Принимая ограничения, можно оценить некоторые рациональные продукты с бесконечным числом факторов и с точки зрения гамма-функции. Из-за Теорема факторизации Вейерштрасса, аналитические функции могут быть записаны как бесконечные произведения, а иногда их можно представить как конечные произведения или частные гамма-функции. Мы уже видели один поразительный пример: формула отражения по существу представляет синусоидальную функцию как произведение двух гамма-функций. Исходя из этой формулы, экспоненциальная функция, а также все тригонометрические и гиперболические функции могут быть выражены через гамма-функцию.

Еще больше функций, включая гипергеометрическая функция и их частные случаи, могут быть представлены с помощью сложных контурные интегралы произведений и частных гамма-функции, называемой Интегралы Меллина – Барнса..

Аналитическая теория чисел

Элегантное и глубокое применение гамма-функции заключается в изучении Дзета-функция Римана. Основным свойством дзета-функции Римана является ее функциональное уравнение:

${displaystyle Gamma left({frac {s}{2}}ight)zeta (s)pi ^{-{frac {s}{2}}}=Gamma left({frac {1-s}{2}}ight)zeta (1-s)pi ^{-{frac {1-s}{2}}}.}$

Среди прочего, это обеспечивает явную форму для аналитическое продолжение дзета-функции до мероморфной функции на комплексной плоскости и приводит к немедленному доказательству того, что дзета-функция имеет бесконечно много так называемых «тривиальных» нулей на действительной прямой. Borwein и другие. называют эту формулу «одним из самых прекрасных открытий в математике».^[32] Другой чемпион этого титула мог бы быть

${displaystyle zeta (s);Gamma (s)=int _{0}^{infty }{frac {t^{s}}{e^{t}-1}},{frac {dt}{t}}.}$

Обе формулы были получены Бернхард Риманн в его основополагающей статье 1859 г. "Über die Anzahl der Primzahlen unter einer gegebenen Größe«(« О количестве простых чисел меньше заданного количества »), одна из вех в развитии аналитическая теория чисел - раздел математики, изучающий простые числа с использованием инструментов математического анализа. Факториальные числа, рассматриваемые как дискретные объекты, являются важным понятием в классической теории чисел, потому что они содержат много простых множителей, но Риман нашел применение их непрерывному расширению, которое, возможно, оказалось даже более важным.

История

Гамма-функция вызвала интерес некоторых из самых выдающихся математиков всех времен. Его история, особенно задокументированная Филип Дж. Дэвис в статье, которая принесла ему премию 1963 г. Приз Шовене, отражает многие из основных достижений математики с 18 века. По словам Дэвиса, «каждое поколение нашло что-то интересное, чтобы сказать о гамма-функции. Возможно, следующее поколение тоже будет».^[1]

18 век: Эйлер и Стирлинг

Даниэль Бернулли письмо к Кристиан Гольдбах 6 октября 1729 г.

Проблема расширения факториала на нецелые аргументы, по-видимому, впервые была рассмотрена Даниэль Бернулли и Кристиан Гольдбах в 1720-х годах, и была решена в конце того же десятилетия Леонард Эйлер. Эйлер дал два разных определения: первое - не его интеграл, а бесконечный продукт,

${displaystyle n!=prod _{k=1}^{infty }{frac {left(1+{frac {1}{k}}ight)^{n}}{1+{frac {n}{k}}}},,}$

о чем он сообщил Гольдбаху в письме от 13 октября 1729 г. Он снова написал Гольдбаху 8 января 1730 г., чтобы объявить о своем открытии интегрального представления

${displaystyle n!=int _{0}^{1}(-ln s)^{n},ds,,}$

что действительно для п > 0. Заменой переменных т = −ln s, это становится знакомым интегралом Эйлера. Эйлер опубликовал свои результаты в статье «De progressionibus transcendentibus seu Quarum termini generales algebraice dari nequeunt» («О трансцендентных прогрессиях, то есть тех, общие термины которых не могут быть даны алгебраически»), представленной в Санкт-Петербургская Академия 28 ноября 1729 г.^[33] Эйлер далее открыл некоторые важные функциональные свойства гамма-функции, включая формулу отражения.

Джеймс Стирлинг, современник Эйлера, также попытался найти непрерывное выражение для факториала и придумал то, что теперь известно как Формула Стирлинга. Хотя формула Стирлинга дает хорошую оценку п!, также для нецелых чисел, он не дает точного значения. Расширения его формулы, исправляющие ошибку, были даны самим Стирлингом и Жак Филипп Мари Бине.

XIX век: Гаусс, Вейерштрасс и Лежандр

Первая страница статьи Эйлера

Карл Фридрих Гаусс переписал произведение Эйлера как

${displaystyle Gamma (z)=lim _{m o infty }{frac {m^{z}m!}{z(z+1)(z+2)cdots (z+m)}}}$

и использовал эту формулу для открытия новых свойств гамма-функции. Хотя Эйлер был пионером в теории комплексных переменных, он, похоже, не рассматривал факториал комплексного числа, как сначала сделал Гаусс.^[34] Гаусс также доказал теорема умножения гамма-функции и исследовали связь между гамма-функцией и эллиптические интегралы.

Карл Вейерштрасс далее установил роль гамма-функции в комплексный анализ, начиная с еще одного товарного представления,

${displaystyle Gamma (z)={frac {e^{-gamma z}}{z}}prod _{k=1}^{infty }left(1+{frac {z}{k}}ight)^{-1}e^{frac {z}{k}},}$

куда γ это Константа Эйлера – Маскерони. Первоначально Вейерштрасс писал свой продукт как продукт для 1/Γ, и в этом случае она берется по нулям функции, а не по ее полюсам. Вдохновленный этим результатом, он доказал то, что известно как Теорема факторизации Вейерштрасса - что любую целую функцию можно записать как произведение над ее нулями на комплексной плоскости; обобщение основная теорема алгебры.

Имя гамма-функции и символ Γ были представлены Адриан-Мари Лежандр около 1811 г .; Лежандр также переписал интегральное определение Эйлера в его современной форме. Хотя символ представляет собой греческую гамму в верхнем регистре, не существует общепринятого стандарта, определяющего, следует ли записывать имя функции «гамма-функция» или «гамма-функция» (некоторые авторы просто пишут «Γ-функция »). Альтернативное обозначение« функция Пи » Π (z) = z! из-за Гаусса иногда встречается в более ранней литературе, но примечания Лежандра преобладают в современных произведениях.

Уместно спросить, почему мы различаем «обычный факториал» и гамма-функцию, используя разные символы, и, в частности, почему гамма-функцию следует нормировать на Γ (п + 1) = п! вместо простого использования "Γ (п) = п!". Считаем, что обозначения показателей, Икс^п, был обобщен от целых чисел до комплексных чисел Икс^z без каких-либо изменений. Мотивация Лежандра к нормализации, по-видимому, не известна, и некоторые (математик 20-го века) критиковали ее как громоздкую. Корнелиус Ланцош, например, назвал его «лишенным всякой рациональности» и вместо этого использовал бы z!).^[35] Нормализация Лежандра действительно упрощает некоторые формулы, но усложняет большинство других. С современной точки зрения, нормализация Лежандра гамма-функции представляет собой интеграл от аддитивной персонаж е^−Икс против мультипликативного характера Икс^z с уважением к Мера Хаара ${displaystyle { frac {dx}{x}}}$ на Группа Ли р⁺. Таким образом, эта нормализация проясняет, что гамма-функция является непрерывным аналогом Сумма Гаусса.

XIX – XX века: характеристика гамма-функции

Несколько проблематично то, что для гамма-функции было дано большое количество определений. Хотя они описывают одну и ту же функцию, доказать эквивалентность не совсем просто. Стирлинг так и не доказал, что его расширенная формула точно соответствует гамма-функции Эйлера; доказательство было впервые дано Чарльз Эрмит в 1900 г.^[36] Вместо того, чтобы искать специализированное доказательство для каждой формулы, было бы желательно иметь общий метод определения гамма-функции.

Один из способов доказать - найти дифференциальное уравнение что характеризует гамма-функцию. Большинство специальных функций в прикладной математике возникают как решения дифференциальных уравнений, решения которых единственны. Однако гамма-функция не удовлетворяет никакому простому дифференциальному уравнению. Отто Гёльдер в 1887 г. доказал, что гамма-функция по крайней мере не удовлетворяет никаким алгебраический дифференциальное уравнение показав, что решение такого уравнения не может удовлетворять рекуррентной формуле гамма-функции, что делает его трансцендентно трансцендентная функция. Этот результат известен как Теорема Гёльдера.

Определенная и общеприменимая характеристика гамма-функции не была дана до 1922 г. Харальд Бор и Йоханнес Моллеруп затем доказал то, что известно как Теорема Бора – Моллерупа: что гамма-функция является единственным решением факторного рекуррентного отношения, которое является положительным и логарифмически выпуклый для положительного z и чье значение в 1 равно 1 (функция является логарифмически выпуклой, если ее логарифм выпуклый). Другая характеристика дается Теорема Виландта.

Теорема Бора – Моллерупа полезна, потому что относительно легко доказать логарифмическую выпуклость для любой из различных формул, используемых для определения гамма-функции. Двигаясь дальше, вместо определения гамма-функции какой-либо конкретной формулой мы можем выбрать в качестве определения условия теоремы Бора – Моллерупа, а затем выбрать любую понравившуюся формулу, которая удовлетворяет условиям, в качестве отправной точки для изучения гамма-функции. . Такой подход был использован Группа Бурбаки.

Borwein И Корлесс^[37] обзор трех столетий работы над гамма-функцией.

Справочные таблицы и программное обеспечение

Хотя гамма-функцию можно вычислить практически так же легко, как любую математически более простую функцию с помощью современного компьютера - даже с помощью программируемого карманного калькулятора - это, конечно, было не всегда. До середины 20 века математики полагались на таблицы, сделанные вручную; в случае гамма-функции, в частности, таблица, вычисленная Гауссом в 1813 году, и таблица, вычисленная Лежандром в 1825 году.

Нарисованный от руки график абсолютного значения комплексной гамма-функции от Таблицы высших функций к Янке и Emde [де ].

Таблицы комплексных значений гамма-функции, а также нарисованные от руки графики приведены в Таблицы высших функций к Янке и Emde [де ], впервые опубликовано в Германии в 1909 году. По данным Майкл Берри, «публикация в J&E трехмерного графика, показывающего полюса гамма-функции в комплексной плоскости, приобрела почти культовый статус».^[38]

На самом деле практической необходимости в чем-либо, кроме реальных значений гамма-функции, не было до 1930-х годов, когда приложения для комплексной гамма-функции были обнаружены в теоретической физике. Когда в 1950-х годах стали доступны электронные компьютеры для производства таблиц, для удовлетворения спроса было опубликовано несколько обширных таблиц для сложной гамма-функции, в том числе таблица с точностью до 12 знаков после запятой из США. Национальное бюро стандартов.^[1]

Абрамовиц и Стегун стал стандартным справочником для этой и многих других специальных функций после его публикации в 1964 году.

Реализации гамма-функции и ее логарифма с плавающей запятой двойной точности теперь доступны в большинстве научных вычислительных программ и, например, в библиотеках специальных функций. TK Solver, Matlab, GNU Octave, а Научная библиотека GNU. Гамма-функция также была добавлена ​​в C стандартная библиотека (math.h ). Реализации произвольной точности доступны в большинстве системы компьютерной алгебры, Такие как Mathematica и Клен. PARI / GP, MPFR и MPFUN содержат бесплатные реализации произвольной точности. Малоизвестная функция калькулятора, входящего в Операционная система Android состоит в том, что он будет принимать дробные значения в качестве входных данных для функции факториала и возвращать эквивалентное значение гамма-функции. То же верно и для Калькулятор Windows (в научном режиме).

Смотрите также

• Восходящий факториал
• Интеграл Каэна – Меллина
• Эллиптическая гамма-функция
• Постоянная Гаусса
• Гамма-функция Адамара
• Множественная гамма-функция
• Многомерная гамма-функция
• п-адическая гамма-функция
• Pochhammer k-символ
• q-гамма-функция
• Основная теорема Рамануджана
• Приближение Спужа

Примечания

1. Дэвис, П. Дж. (1959). "Интеграл Леонарда Эйлера: исторический профиль гамма-функции". Американский математический ежемесячный журнал. 66 (10): 849–869. Дои:10.2307/2309786. JSTOR  2309786. Получено 3 декабря 2016.
2. Билс, Ричард; Вонг, Родерик (2010). Специальные функции: выпускной текст. Издательство Кембриджского университета. п. 28. ISBN  978-1-139-49043-6. Отрывок страницы 28
3. Росс, Клэй С. (2013). Дифференциальные уравнения: введение в систему Mathematica (иллюстрированный ред.). Springer Science & Business Media. п. 293. ISBN  978-1-4757-3949-7. Выражение G.2 на странице 293
4. Кингман, Дж. Ф. С. (1961). «Свойство выпуклости положительных матриц». Ежеквартальный журнал математики. 12 (1): 283–284. Bibcode:1961QJMat..12..283K. Дои:10.1093 / qmath / 12.1.283.
5. Вайсштейн, Эрик В. "Теорема Бора – Моллерупа". MathWorld.
6. Аски, Р.А.; Рой, Р. (2010), «Расширения серий», в Олвер, Фрэнк В. Дж.; Lozier, Daniel M .; Boisvert, Рональд Ф .; Кларк, Чарльз В. (ред.), Справочник NIST по математическим функциям, Издательство Кембриджского университета, ISBN  978-0-521-19225-5, МИСТЕР  2723248
7. Вальдшмидт, М. (2006). "Превосходство эпох: современное состояние" (PDF). Pure Appl. Математика. Кварта. 2 (2): 435–463. Дои:10.4310 / pamq.2006.v2.n2.a3.
8. Вайсштейн, Эрик В. «Гамма-функция». MathWorld.
9. Уиттакер и Ватсон, 12.2, пример 1.
10. Уиттакер и Ватсон, 31.12.
11. Уиттакер и Ватсон, 12.32.
12. Уиттакер и Ватсон, 22.12.
13. Бейтман, Гарри; Эрдейи, Артур (1955). Высшие трансцендентные функции. Макгроу-Хилл.
14. Srivastava, H.M .; Чой, Дж. (2001). Серии, связанные с Зетами, и связанные с ними функции. Нидерланды: Kluwer Academic.
15. Благушин, Ярослав В. (2014). «Повторное открытие интегралов Мальмстена, их вычисление методами контурного интегрирования и некоторые связанные результаты». Рамануджан Дж.. 35 (1): 21–110. Дои:10.1007 / s11139-013-9528-5.
16. Благушин, Ярослав В. (2016). "Исправление и дополнение к" Повторное открытие интегралов Мальмстена, их оценка методами контурного интегрирования и некоторые связанные результаты"". Рамануджан Дж.. 42 (3): 777–781. Дои:10.1007 / s11139-015-9763-z.
17. «Журнал гамма-функции». Вольфрам MathWorld. Получено 3 января 2019.
18. Благушин, Ярослав В. (2015). «Теорема для вычисления в закрытой форме первой обобщенной постоянной Стилтьеса при рациональных аргументах и ​​некоторых связанных суммирования». Журнал теории чисел. 148: 537–592. arXiv:1401.3724. Дои:10.1016 / j.jnt.2014.08.009.
19. Алексеевский, В. П. (1894). "Über eine Classe von Funktionen, die der Gammafunktion analog sind" [О классе функций, аналогичных гамма-функции]. Лейпциг Weidmanncshe Buchhandluns. 46: 268–275.
20. Барнс, Э. У. (1899). "Теория грамм-функция ». Кварта. J. Math. 31: 264–314.
21. Адамчик, Виктор С. (1998). «Полигамма функции отрицательного порядка». J. Comput. Appl. Математика. 100 (2): 191–199. Дои:10.1016 / S0377-0427 (98) 00192-7.
22. Госпер, Р. В. (1997). "${displaystyle extstyle int _{n/4}^{m/6}log F(z),dz}$ в специальных функциях, q-серии и сопутствующие темы ». Варенье. Математика. Soc. 14.
23. Эспиноза, Оливье; Молл, Виктор Х. (2002). «О некоторых интегралах, включающих дзета-функцию Гурвица: Часть 1». Рамануджанский журнал. 6: 159–188. Дои:10.1023 / А: 1015706300169.
24. Бейли, Дэвид Х .; Борвейн, Дэвид; Борвейн, Джонатан М. (2015). «Об эйлеровых лог-гамма-интегралах и дзета-функциях Торнхейма-Виттена». Рамануджанский журнал. 36: 43–68. Дои:10.1007 / s11139-012-9427-1.
25. Amdeberhan, T .; Коффи, Марк В .; Эспиноза, Оливье; Кутшан, Кристоф; Manna, Dante V .; Молл, Виктор Х. (2011). «Интегралы по степеням логгаммы». Proc. Амер. Математика. Soc. 139 (2): 535–545. Дои:10.1090 / S0002-9939-2010-10589-0.
26. E.A. Карацуба, Быстрое вычисление трансцендентных функций. Пробл. Инф. Трансм. Том 27, № 4, стр. 339–360 (1991).
27. E.A. Карацуба, О новом методе быстрого вычисления трансцендентных функций. Русь. Математика. Surv. Том 46, № 2, стр. 246–247 (1991).
28. E.A. Карацуба »Быстрые алгоритмы и метод FEE ".
29. Мишон, Г. П. "Тригонометрия и основные функции В архиве 9 января 2010 г. Wayback Machine ". Numericana. Проверено 5 мая 2007 года.
30. Чаудри, М.А., Зубайр, С.М. (2001). Об одном классе неполных гамма-функций с приложениями. п. 37
31. Райс, Дж. А. (1995). Математическая статистика и анализ данных (Второе издание). п. 52–53
32. Borwein, J .; Бэйли, Д. Х. и Гирдженсон, Р. (2003). Эксперименты по математике. А. К. Петерс. п. 133. ISBN  978-1-56881-136-9.
33. Статья Эйлера была опубликована в Commentarii academiae scientiarum Petropolitanae 5, 1738, 36–57. Видеть E19 - De progressionibus transcendentibus seu quum termini generales algebraice dari nequeunt из архива Эйлера, который включает сканированную копию оригинальной статьи.
34. Реммерт, Р. (2006). Классические темы теории сложных функций. Перевод Кея, Л. Д. Спрингера. ISBN  978-0-387-98221-2.
35. Ланцош, К. (1964). «Прецизионная аппроксимация гамма-функции». J. SIAM Numer. Анальный. Сер. B. 1.
36. Кнут, Д. Э. (1997). Искусство программирования, Том 1 (Фундаментальные алгоритмы). Эддисон-Уэсли.
37. Борвейн, Джонатан М.; Корлесс, Роберт М. (2017). «Гамма и факториал в месяц». Американский математический ежемесячный журнал. Математическая ассоциация Америки. 125 (5): 400–24. arXiv:1703.05349. Bibcode:2017arXiv170305349B. Дои:10.1080/00029890.2018.1420983.
38. Берри, М. (апрель 2001 г.). "Почему специальные функции особенные?". Физика сегодня.

• В этой статье использованы материалы из Citizendium статья "Гамма-функция "под лицензией Creative Commons Attribution-ShareAlike 3.0 Непортированная лицензия но не под GFDL.

дальнейшее чтение

• Абрамовиц, Милтон; Стегун, Ирен А., ред. (1972). "Глава 6". Справочник по математическим функциям с формулами, графиками и математическими таблицами. Нью-Йорк: Дувр.
• Эндрюс, Г. Э.; Askey, R .; Рой, Р. (1999). «Глава 1 (Гамма и бета-функции)». Специальные функции. Нью-Йорк: Издательство Кембриджского университета. ISBN  978-0-521-78988-2.
• Артин, Эмиль (2006). «Гамма-функция». В Розен, Майкл (ред.). Экспозиция Эмиля Артина: подборка. История математики. 30. Провиденс, Род-Айленд: Американское математическое общество.
• Аски, Р.; Рой, Р. (2010), «Гамма-функция», в Олвер, Фрэнк В. Дж.; Lozier, Daniel M .; Boisvert, Рональд Ф .; Кларк, Чарльз В. (ред.), Справочник NIST по математическим функциям, Издательство Кембриджского университета, ISBN  978-0-521-19225-5, МИСТЕР  2723248
• Биркофф, Джордж Д. (1913). «Примечание о гамма-функции». Бык. Амер. Математика. Soc. 20 (1): 1–10. Дои:10.1090 / s0002-9904-1913-02429-7. МИСТЕР  1559418.
• Бёмер, П. Э. (1939). Differenzengleichungen und bestimmte Integrale [Дифференциальные уравнения и определенные интегралы.]. Лейпциг: Köhler Verlag.
• Дэвис, Филип Дж. (1959). "Интеграл Леонарда Эйлера: исторический профиль гамма-функции". Американский математический ежемесячный журнал. 66 (10): 849–869. Дои:10.2307/2309786. JSTOR  2309786.
• Press, W. H .; Теукольский, С. А .; Vetterling, W. T .; Фланнери, Б. П. (2007). «Раздел 6.1. Гамма-функция». Числовые рецепты: искусство научных вычислений (3-е изд.). Нью-Йорк: Издательство Кембриджского университета. ISBN  978-0-521-88068-8.
• Rocktäschel, О. Р. (1922). Methoden zur Berechnung der Gammafunktion für komplexes Аргумент [Методы вычисления гамма-функции для сложных аргументов]. Дрезден: Технический университет Дрездена.
• Темме, Нико М. (1996). Специальные функции: введение в классические функции математической физики. Нью-Йорк: Джон Вили и сыновья. ISBN  978-0-471-11313-3.
• Уиттакер, Э. Т.; Уотсон, Г.Н. (1927). Курс современного анализа. Издательство Кембриджского университета. ISBN  978-0-521-58807-2.

внешняя ссылка

• Цифровая библиотека математических функций NIST: гамма-функция
• Паскаль Себа и Ксавье Гурдон. Введение в гамма-функцию. В PostScript и HTML форматы.
• Справочник по C ++ для std :: tgamma
• Примеры проблем, связанных с гамма-функцией, можно найти на Exampleproblems.com.
• «Гамма-функция», Энциклопедия математики, EMS Press, 2001 [1994]
• Оценщик гамма-функции Wolfram (произвольная точность)
• "Гамма". Вольфрам Функции сайта.
• Объем n-сфер и гамма-функция на MathPages