Теорема Тейлорса - Taylors theorem
| Часть цикла статей о | ||||||
| Исчисление | ||||||
|---|---|---|---|---|---|---|
| ||||||
| ||||||
В исчисление, Теорема Тейлора дает приближение к k-раз дифференцируемая функция вокруг заданной точки многочлен степени k, называется kй порядок Полином Тейлора. Для гладкая функция, многочлен Тейлора - это усечение по порядку k из Серия Тейлор функции. Многочлен Тейлора первого порядка - это линейное приближение функции, а многочлен Тейлора второго порядка часто называют квадратичное приближение.[1] Существует несколько версий теоремы Тейлора, некоторые из которых дают явные оценки ошибки приближения функции ее полиномом Тейлора.
Теорема Тейлора названа в честь математика Брук Тейлор, который изложил версию этого в 1715 году,[2] хотя более ранняя версия результата уже упоминалась в 1671 к Джеймс Грегори.[3]
Теорема Тейлора преподается на вводных курсах по исчислению и является одним из основных элементарных инструментов в математический анализ. Он дает простые арифметические формулы для точного вычисления значений многих трансцендентные функции такой как экспоненциальная функция и тригонометрические функции.Это отправная точка изучения аналитические функции, и является фундаментальным в различных областях математики, а также в числовой анализ и математическая физика. Теорема Тейлора также обобщается на многомерный и вектор оценен функции.
Мотивация

Если ценный функция ж(Икс) является дифференцируемый в момент Икс = а, то у него линейное приближение рядом с этой точкой. Это означает, что существует функция час1(Икс) такие, что
Здесь
является линейным приближением ж(Икс) за Икс рядом с точкой а, чей график у = п1(Икс) это касательная линия графику y = ж(Икс) в Икс = а. Ошибка в приближении:
В качестве Икс как правилоа, эта ошибка обращается в ноль намного быстрее, чем , изготовление полезное приближение.

Для лучшего приближения к ж(Икс), мы можем уместить квадратичный многочлен вместо линейной функции:
Вместо того, чтобы просто сопоставить одну производную от ж(Икс) в Икс = а, этот многочлен имеет одни и те же первую и вторую производные, что видно при дифференцировании.
Теорема Тейлора гарантирует, что квадратичное приближение находится в достаточно малой окрестности точки х = а, более точный, чем линейное приближение. Конкретно,
Здесь ошибка приближения равна
что, учитывая предельное поведение , переходит в ноль быстрее, чем в качестве Икс как правилоа.

Точно так же мы могли бы получить еще лучшие приближения к ж если мы используем многочлены более высокой степени, с тех пор мы можем сопоставить еще больше производных с ж в выбранной базовой точке.
В общем случае ошибка приближения функции полиномом степени k обнулится намного быстрее, чем в качестве Икс как правилоа. Однако есть функции, даже бесконечно дифференцируемые, для которых увеличение степени аппроксимирующего полинома не увеличивает точность приближения: мы говорим, что такая функция не может быть аналитический в х = а: он не определяется (локально) своими производными в этой точке.
Теорема Тейлора имеет асимптотический характер: она только говорит нам, что ошибка рk в приближение по kмногочлен Тейлора -го порядка пk стремится к нулю быстрее любого ненулевого k-я степень многочлен в качестве Икс → а. Это не говорит нам, насколько велика ошибка в каком-либо конкретном район центра расширения, но для этой цели существуют явные формулы для остаточного члена (приведенные ниже), которые справедливы при некоторых дополнительных предположениях регулярности ж. Эти расширенные версии теоремы Тейлора обычно приводят к единые оценки для ошибки приближения в малой окрестности центра расширения, но оценки не обязательно верны для слишком больших окрестностей, даже если функция ж является аналитический. В этой ситуации, возможно, придется выбрать несколько полиномов Тейлора с разными центрами разложения, чтобы получить надежные Тейлоровские приближения исходной функции (см. Анимацию справа).
Остающийся термин можно использовать несколькими способами:
- Оцените ошибку полинома пk(Икс) степени k оценка ж(Икс) на заданном интервале (а – р, а + р). (Учитывая интервал и степень, мы находим ошибку.)
- Найдите наименьшую степень k для которого многочлен пk(Икс) приблизительно ж(Икс) с точностью до заданного допуска ошибок на заданном интервале (а − р, а + р). (Учитывая интервал и допустимую погрешность, мы находим степень.)
- Найдите наибольший интервал (а − р, а + р) на котором пk(Икс) приблизительно ж(Икс) с точностью до заданной погрешности. (Учитывая степень и допуск ошибок, мы находим интервал.)
Теорема Тейлора с одной действительной переменной
Формулировка теоремы
Точная формулировка основной версии теоремы Тейлора выглядит следующим образом:
Теорема Тейлора.[4][5][6] Позволять k ≥ 1 быть целое число и пусть функция ж : р → р быть k раз дифференцируемый в момент а ∈ р. Тогда существует функция часk : р → р такой, что
. Это называется Пеано форма остатка.
Многочлен, фигурирующий в теореме Тейлора, - это kмногочлен Тейлора -го порядка
функции ж в момент а. Многочлен Тейлора является единственным полиномом «асимптотического наилучшего соответствия» в том смысле, что если существует функция часk : р → р и kмногочлен -го порядка п такой, что
тогда п = пk. Теорема Тейлора описывает асимптотическое поведение оставшийся срок
какой ошибка приближения при приближении ж с его многочленом Тейлора. С использованием маленькая нотация, утверждение теоремы Тейлора читается как
Явные формулы для остатка
При более сильных предположениях регулярности ж есть несколько точных формул для остаточного члена рk полинома Тейлора, наиболее распространенными из которых являются следующие.
Средневзвешенная форма остатка. Позволять ж : р → р быть k +1 раз дифференцируемый на открытый интервал с ж(k) непрерывный на закрытый интервал между а и Икс.[7] потом
для какого-то реального числа ξL между а и Икс. Это Лагранж форма[8] от остатка.
По аналогии,
для какого-то реального числа ξC между а и Икс. Это Коши форма[9] от остатка.
Эти уточнения теоремы Тейлора обычно доказываются с использованием теорема о среднем значении, откуда и название. Также можно найти другие подобные выражения. Например, если грамм(т) непрерывна на отрезке и дифференцируема с отличной от нуля производной на отрезке между а и Икс, тогда
для некоторого числа ξ между а и Икс. Эта версия охватывает формы Лагранжа и Коши остатка как частные случаи и доказывается ниже с использованием Теорема Коши о среднем значении.
Утверждение для интегральной формы остатка более продвинуто, чем предыдущие, и требует понимания Теория интеграции Лебега для полной общности. Однако это справедливо и в смысле Интеграл Римана при условии (k + 1) -я производная от ж непрерывна на отрезке [а,Икс].
Целостная форма остатка.[10] Позволять ж(k) быть абсолютно непрерывный на закрытый интервал между а и Икс. потом
Из-за абсолютная непрерывность из ж(k) на закрытый интервал между а и Икс, его производная ж(k+1) существует как L1-функция, и результат может быть доказан формальным расчетом с использованием основная теорема исчисления и интеграция по частям.
Оценки остатка
На практике часто бывает полезно иметь возможность оценить остаточный член, появляющийся в приближении Тейлора, вместо того, чтобы иметь для него точную формулу. Предположим, что ж является (k + 1)-время непрерывно дифференцируемые в интервале я содержащий а. Предположим, что существуют действительные постоянные q и Q такой, что
на протяжении я. Тогда остаточный член удовлетворяет неравенству[11]
если Икс > а, и аналогичная оценка, если Икс < а. Это простое следствие формы Лагранжа остатка. В частности, если
на интервале я = (а − р,а + р) с некоторыми , тогда
для всех Икс∈(а − р,а + р). Второе неравенство называется единая оценка, поскольку он выполняется равномерно для всех Икс на интервале (а − р,а + р).
Пример
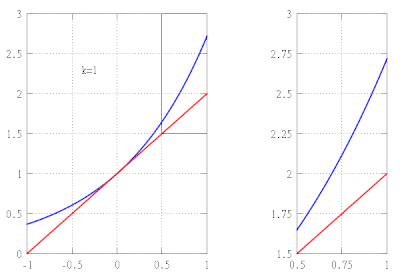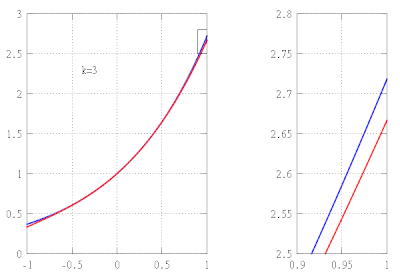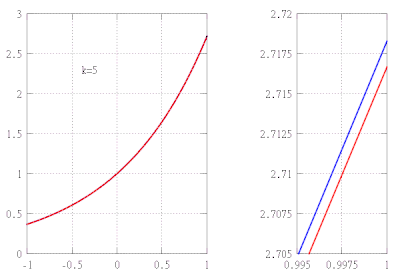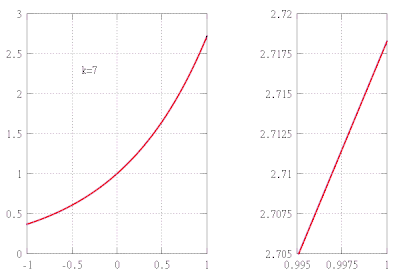
Предположим, мы хотим найти приближенное значение функции ж(Икс) = еИкс на интервале [−1,1] при обеспечении погрешности аппроксимации не более 10−5. В этом примере мы делаем вид, что знаем только следующие свойства экспоненциальной функции:
Из этих свойств следует, что ж(k)(Икс) = еИкс для всех k, и в частности, ж(k)(0) = 1. Следовательно kмногочлен Тейлора ж в 0, а его остаточный член в форме Лагранжа имеет вид
куда ξ какое-то число от 0 до Икс. С еИкс увеличивается на (*), мы можем просто использовать еИкс ≤ 1 для Икс ∈ [−1, 0], чтобы оценить остаток на подынтервале [−1, 0]. Чтобы получить оценку сверху остатка на [0,1], воспользуемся свойством еξ<еИкс для 0 <ξ <х чтобы оценить
используя разложение Тейлора второго порядка. Затем мы решаем для еИкс вывести это
просто за счет максимизации числитель и минимизация знаменатель. Комбинируя эти оценки для еИкс Мы видим, что
так что требуемая точность обязательно достигается, когда
(Видеть факториал или вычислите вручную значения 9! = 362 880 и 10! = 3 628 800.) В заключение, теорема Тейлора приводит к приближению
Например, это приближение дает десятичное выражение е ≈ 2,71828, исправьте до пяти десятичных знаков.
Отношение к аналитичности
Разложения Тейлора вещественных аналитических функций
Позволять я ⊂ р быть открытый интервал. По определению функция ж : я → р является настоящий аналитик если он локально определяется сходящейся степенной ряд. Это означает, что для каждого а ∈ я есть некоторые р > 0 и последовательность коэффициентов ck ∈ р такой, что (а − р, а + р) ⊂ я и
В целом радиус схождения степенного ряда можно вычислить из Формула Коши – Адамара
Этот результат основан на сравнении с геометрическая серия, и тот же метод показывает, что если степенной ряд на основе а сходится для некоторых б ∈ р, он должен сходиться равномерно на закрытый интервал [а − рб, а + рб], куда рб = |б − а|, Здесь рассматривается только сходимость степенного ряда, и вполне может быть, что (а − р,а + р) выходит за пределы области я из ж.
Многочлены Тейлора вещественной аналитической функции ж в а просто конечные усечения
его локально определяющего степенного ряда, а соответствующие остаточные члены локально задаются аналитическими функциями
Здесь функции
также являются аналитическими, поскольку их определяющий степенной ряд имеет тот же радиус сходимости, что и исходный ряд. При условии, что [а − р, а + р] ⊂ я и р < р, все эти ряды равномерно сходятся на (а − р, а + р). Естественно, что в случае аналитических функций можно оценить остаточный член рk(Икс) хвостом последовательности производных f ′(а) в центре расширения, но используя комплексный анализ также возникает другая возможность, которая описана ниже.
Теорема Тейлора и сходимость рядов Тейлора
Серия Тейлора ж будет сходиться в некотором интервале, в котором все его производные ограничены и не растут слишком быстро при k уходит в бесконечность. (Однако даже если ряд Тейлора сходится, он может не сходиться к ж, как объяснено ниже; ж тогда говорят, что неаналитический.)
Можно подумать о сериале Тейлора
бесконечно много раз дифференцируемой функции ж : р → р как его «многочлен Тейлора бесконечного порядка» в а. Теперь оценки на остаток подразумевают, что если для любого р, производные от ж известны как ограниченные над (а − р, а + р), то для любого порядка k и для любого р > 0 существует постоянная Mk, r > 0 такой, что
для каждого Икс ∈ (а − р,а + р). Иногда константы Mk, r можно выбрать так, что Mk, r ограничено сверху, при фиксированном р и все k. Затем серия Тейлора ж сходится равномерно к некоторой аналитической функции
(Сходимость также получается, даже если Mk, r не ограничивается сверху, пока растет достаточно медленно.)
Предельная функция Тж по определению всегда аналитический, но он не обязательно равен исходной функции ж, даже если ж легко дифференцируемо. В этом случае мы говорим ж это неаналитическая гладкая функция, например плоская функция:
С использованием Правило цепи неоднократно математическая индукция, показывает, что для любого заказаk,
для некоторого полинома пk степени 2 (k - 1). Функция стремится к нулю быстрее любого полинома при Икс → 0, так ж бесконечно много раз дифференцируема и ж(k)(0) = 0 для каждого положительного целого числа k. Все приведенные выше результаты верны в этом случае:
- Серия Тейлора ж равномерно сходится к нулевой функции Тж(Икс) = 0, что аналитично со всеми равными нулю коэффициентами.
- Функция ж не равен этому ряду Тейлора и, следовательно, неаналитичен.
- На любой заказ k ∈ N и радиус р > 0 существует Mk, r > 0, удовлетворяющий оценке остатка (*) выше.
Однако, как k увеличивается на фиксированные р, значение Mk, r растет быстрее, чем рk, а ошибка не обращается в ноль.
Теорема Тейлора в комплексном анализе
Теорема Тейлора обобщается на функции ж : C → C которые комплексно дифференцируемый в открытом подмножестве U ⊂ C из комплексная плоскость. Однако его полезность затмевается другими общими теоремами из комплексный анализ. А именно, более сильные версии связанных результатов могут быть выведены для комплексно дифференцируемый функции ж : U → C с помощью Интегральная формула Коши следующее.
Позволять р > 0 такой, что закрытый диск B(z, р) ∪ S(z, р) содержится в U. Тогда интегральная формула Коши с положительной параметризацией γ(т)=z + повторноЭто круга S(z, р) с т ∈ [0, 2π] дает
Здесь все подынтегральные выражения непрерывны на круг S(z, р), что оправдывает дифференцирование под знаком интеграла. В частности, если ж однажды комплексно дифференцируемый на открытой площадке U, то на самом деле бесконечно много раз комплексно дифференцируемый на U. Также получаются оценки Коши[12]
для любого z ∈ U и р > 0 такой, что B(z, р) ∪ S(c, р) ⊂ U. Из этих оценок следует, что сложный Серия Тейлор
из ж сходится равномерно на любом открытый диск B(c, р) ⊂ U с S(c, р) ⊂ U в какую-то функцию Тж. Кроме того, используя формулы контурного интеграла для производных ж(k)(c),
так что любой комплексно дифференцируемый функция ж в открытом наборе U ⊂ C на самом деле комплексный аналитический. Все, что сказано о вещественных аналитических функциях здесь выполняется также для комплексных аналитических функций с открытым интервалом я заменено открытым подмножеством U ∈ C и а-центрированные интервалы (а − р, а + р) заменен на c-центрированные диски B(c, р). В частности, разложение Тейлора имеет вид
где остаток рk комплексно аналитический. Методы комплексного анализа дают некоторые убедительные результаты в отношении разложений Тейлора. Например, используя интегральную формулу Коши для любого положительно ориентированного Кривая Иордании γ который параметризует границу ∂W ⊂ U региона W ⊂ U, получаем выражения для производных ж(j)(c) как указано выше, и немного изменив расчет для Тж(z) = ж(z), приходим к точной формуле
Важной особенностью здесь является то, что качество приближения полиномом Тейлора на области W ⊂ U преобладают значения функции ж сам на границе ∂W ⊂ U. Аналогично, применяя оценки Коши к выражению ряда для остатка, получаем равномерные оценки
Пример

Функция
является настоящий аналитик, то есть локально определяется своим рядом Тейлора. Эта функция была построена над чтобы проиллюстрировать тот факт, что некоторые элементарные функции не могут быть приближены полиномами Тейлора в слишком больших окрестностях центра расширения. Такое поведение легко понять в рамках комплексного анализа. А именно функция ж простирается в мероморфная функция
на компактифицированной комплексной плоскости. Имеет простые полюса на z = я и z = −я, и это аналитическое в другом месте. Теперь его серия Тейлора сосредоточена на z0 сходится на любом диске B(z0, р) с р < |z − z0|, где тот же ряд Тейлора сходится в z ∈ C. Следовательно, ряд Тейлора ж с центром в 0 сходится на B(0, 1) и не сходится ни при каких z ∈ C с |z| > 1 из-за полюсов на я и -я. По той же причине серия Тейлора. ж с центром в 1 сходится на B(1, √2) и не сходится ни при каких z ∈ C с |z − 1| > √2.
Обобщения теоремы Тейлора
Дифференцируемость высшего порядка
Функция ж: рп → р является дифференцируемый в а ∈ рп если и только если существует линейный функционал L : рп → р и функция час : рп → р такой, что
Если это так, то L = df(а) является (однозначно определенным) дифференциал из ж в момент а. Кроме того, тогда частные производные из ж существовать в а и дифференциал ж в а дан кем-то
Представьте многоиндексная запись
за α ∈ Nп и Икс ∈ рп. Если все k-й порядок частные производные из ж : рп → р непрерывны на а ∈ рп, затем по Теорема Клеро, можно изменить порядок смешанных производных при а, поэтому обозначение
для высшего порядка частные производные оправдано в данной ситуации. То же верно, если все (k - частные производные 1) -го порядка от ж существуют в некоторой окрестности а и дифференцируемы на а.[13] Затем мы говорим, что ж является k раз дифференцируемые в точкеа.
Теорема Тейлора для функций многих переменных
Многомерная версия теоремы Тейлора.[14] Позволять ж : рп → р быть k-размерно дифференцируемая функция в точке а∈рп. Тогда существует часα : рп→р такой, что
Если функция ж : рп → р является k +1 раз непрерывно дифференцируемый в закрытый мяч для некоторых , то можно вывести точную формулу для остатка через (k+1) -й порядок частные производные из ж в этом районе.[15] А именно,
В этом случае из-за непрерывность из (k+1) -го порядка частные производные в компактный набор B, сразу получаем равномерные оценки
Пример в двух измерениях
Например, полином Тейлора третьего порядка гладкой функции ж: р2 → р есть, обозначая Икс − а = v,
Доказательства
Доказательство теоремы Тейлора с одной действительной переменной
Позволять[16]
где, как в формулировке теоремы Тейлора,
Достаточно показать, что
Доказательство здесь основано на многократном применении Правило L'Hôpital. Обратите внимание, что для каждого j = 0,1,...,k−1, . Следовательно, каждый из первых k−1 производная числителя в исчезает в , и то же самое верно и для знаменателя. Кроме того, поскольку условие, что функция ж быть k раз дифференцируемые в точке требует дифференцируемости до порядка k−1 в окрестности указанной точки (это верно, потому что дифференцируемость требует, чтобы функция была определена во всей окрестности точки), числитель и его k - 2 производные дифференцируемы в окрестности а. Ясно, что знаменатель также удовлетворяет указанному условию и, кроме того, не обращается в нуль, если Икс=а, поэтому все условия, необходимые для правила L'Hopital, выполнены, и его использование оправдано. Так
где предпоследнее равенство следует из определения производной в точкеИкс = а.
Вывод форм среднего значения остатка
Позволять грамм - любая действительная функция, непрерывная на отрезке между а и Икс и дифференцируемым с отличной от нуля производной на открытом интервале между а и Икс, и определим
За . Затем по Теорема Коши о среднем значении,
для некоторого ξ на открытом интервале между а и Икс. Обратите внимание, что здесь числитель F(Икс) − F(а) = рk(Икс) является в точности остатком от полинома Тейлора для ж(Икс). Вычислить
вставьте его в (*) и переставьте термины, чтобы найти, что
Это форма остаточного члена, упомянутого после фактического утверждения теоремы Тейлора с остатком в форме среднего значения. Форма Лагранжа остатка находится путем выбора и форму Коши, выбрав .
Замечание. Используя этот метод, можно также восстановить интегральный вид остатка, выбрав
но требования к ж необходимые для использования теоремы о среднем значении, слишком сильны, если кто-то стремится доказать утверждение в случае, что ж(k) только абсолютно непрерывный. Однако, если использовать Интеграл Римана вместо Интеграл Лебега, предположения не могут быть ослаблены.
Вывод интегральной формы остатка
Из-за абсолютная непрерывность из ж(k) на закрытый интервал между а и Икс его производная ж(k+1) существует как L1-функция, и мы можем использовать основная теорема исчисления и интеграция по частям. Это же доказательство применимо к Интеграл Римана при условии, что ж(k) является непрерывный на закрытом интервале и дифференцируемый на открытый интервал между а и Икс, и это приводит к тому же результату, что и использование теоремы о среднем значении.
В основная теорема исчисления утверждает, что
Теперь мы можем интегрировать по частям и снова воспользуемся основной теоремой исчисления, чтобы убедиться, что
что в точности является теоремой Тейлора с остатком в интегральной форме в случае k = 1Общее утверждение доказывается с использованием индукция. Предположим, что
Интегрируя остаток по частям, получаем
Подставляя это в формулу в (*) показывает, что если это верно для значения k, он также должен соответствовать значению k + 1, следовательно, поскольку это верно для k = 1, оно должно выполняться для любого положительного целого числаk.
Вывод остатка многомерных многочленов Тейлора
Докажем частный случай, когда ж : рп → р имеет непрерывные частные производные до порядка k+1 в закрытом шаре B с центром а. Стратегия доказательства состоит в применении случая одной переменной теоремы Тейлора к ограничению ж к отрезку линии, примыкающему Икс и а.[17] Параметризуйте отрезок линии между а и Икс к ты(т) = а + т(Икс − а). Применим вариант теоремы Тейлора с одной переменной к функции грамм(т) = ж(ты(т)):
Применяя Правило цепи для нескольких переменных дает
куда это полиномиальный коэффициент. С , мы получили:
Смотрите также
Сноски
- ^ (2013). «Линейно-квадратичное приближение» Проверено 6 декабря 2018 г.
- ^ Тейлор, Брук (1715). Methodus Incrementorum Directa et Inversa [Прямые и обратные методы увеличения] (на латыни). Лондон. п. 21–23 (Предложение VII, Теория 3, Кор. 2). Переведено на английский язык Струик, Д. Дж. (1969). Справочник по математике 1200–1800 гг.. Кембридж, Массачусетс: Издательство Гарвардского университета. С. 329–332.
- ^ Клайн 1972, п. 442, 464.
- ^ Дженокки, Анджело; Пеано, Джузеппе (1884), Дифференциальный кальколо и принцип интеграции кальколо, (№ 67, стр. XVII – XIX): Fratelli Bocca ed.CS1 maint: location (связь)
- ^ Спивак Михаил (1994), Исчисление (3-е изд.), Хьюстон, Техас: Publish or Perish, p. 383, г. ISBN 978-0-914098-89-8
- ^ «Формула Тейлора», Энциклопедия математики, EMS Press, 2001 [1994]
- ^ Гипотеза ж(k) существование непрерывный на закрыто интервал между а и Икс является нет избыточный. Несмотря на то что ж существование k +1 раз дифференцируемый на открытый интервал между а и Икс подразумевает, что ж(k) является непрерывный на открыто интервал между а и Икс, оно делает нет подразумевают, что ж(k) является непрерывный на закрыто интервал между а и Икс, т.е. это не означает, что ж(k) является непрерывный на конечные точки этого интервала. Рассмотрим, например, функция ж : [0,1] → р определяется как равный на и с . Это не непрерывный в 0, но это непрерывный на . Более того, можно показать, что это функция имеет первообразный. Следовательно, что первообразный является дифференцируемый на , это производная (функция ж) является непрерывный на открыто интервал , но это производная ж является нет непрерывный на закрыто интервал . Так что в этом случае теорема неприменима.
- ^ Клайн 1998, §20.3; Апостол 1967, §7.7.
- ^ Апостол 1967, §7.7.
- ^ Апостол 1967, §7.5.
- ^ Апостол 1967, §7.6
- ^ Рудин 1987, §10.26
- ^ Это следует из повторного применения теоремы о том, что если частные производные функции ж существуют в окрестностях а и продолжаются при а, то функция дифференцируема при а. См., Например, Апостол 1974, Теорема 12.11.
- ^ Кенигсбергерский анализ 2, стр. 64 сл.
- ^ https://sites.math.washington.edu/~folland/Math425/taylor2.pdf
- ^ Стромберг 1981
- ^ Хёрмандер 1976, стр. 12–13
Рекомендации
- Апостол, Том (1967), Исчисление, Wiley, ISBN 0-471-00005-1.
- Апостол, Том (1974), Математический анализ, Эддисон – Уэсли.
- Бартл, Роберт Дж .; Шерберт, Дональд Р. (2011), Введение в реальный анализ (4-е изд.), Wiley, ISBN 978-0-471-43331-6.
- Хёрмандер, Л. (1976), Линейные дифференциальные операторы с частными производными, том 1, Спрингер, ISBN 978-3-540-00662-6.
- Клайн, Моррис (1972), Математическая мысль от древних до наших дней, Том 2, Oxford University Press.
- Клайн, Моррис (1998), Исчисление: интуитивный и физический подход, Дувр, ISBN 0-486-40453-6.
- Педрик, Джордж (1994), Первый курс анализа, Спрингер, ISBN 0-387-94108-8.
- Стромберг, Карл (1981), Введение в классический реальный анализ, Уодсворт, ISBN 978-0-534-98012-2.
- Рудин, Вальтер (1987), Реальный и комплексный анализ (3-е изд.), McGraw-Hill, ISBN 0-07-054234-1.
- Тао, Теренс (2014), Анализ, Том I (3-е изд.), Книжное агентство Индостана, ISBN 978-93-80250-64-9.
внешняя ссылка
- Теорема Тейлора в ProofWiki
- Приближение ряда Тейлора к косинусу в завязать узел
- Тригонометрическое разложение Тейлора интерактивный демонстрационный апплет
- Возвращение к серии Тейлора в Институт целостных численных методов







































































![{ Displaystyle т в [а, х]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/357000ec9c6100c2feacc3ca061fa2b3c854be00)









![{ displaystyle { begin {align} int _ {a} ^ {x} { frac {f ^ {(k + 1)} (t)} {k!}} (xt) ^ {k} , dt = & - left [{ frac {f ^ {(k + 1)} (t)} {(k + 1) k!}} (xt) ^ {k + 1} right] _ {a} ^ {x} + int _ {a} ^ {x} { frac {f ^ {(k + 2)} (t)} {(k + 1) k!}} (xt) ^ {k + 1 } , dt = & { frac {f ^ {(k + 1)} (a)} {(k + 1)!}} (xa) ^ {k + 1} + int _ {a } ^ {x} { frac {f ^ {(k + 2)} (t)} {(k + 1)!}} (xt) ^ {k + 1} , dt. end {выровнено}} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/a6389635717cc93be2b76539da45a18411376e16)






![{ displaystyle (0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7e70f9c241f9faa8e9fdda2e8b238e288807d7a4)


![[0,1]](https://wikimedia.org/api/rest_v1/media/math/render/svg/738f7d23bb2d9642bab520020873cccbef49768d)