Теория струнного поля - String field theory

Теория струнного поля (SFT) - формализм в теория струн в котором динамика релятивистский строки переформулированы на языке квантовая теория поля. Это достигается на уровне теория возмущений найдя набор вершин для соединения и разделения строк, а также строку пропагаторы, которые дают Диаграмма Фейнмана -подобное разложение для струнных амплитуд рассеяния. В большинстве теорий строкового поля это расширение кодируется классическое действие найден вторичное квантование свободная строка и добавление условий взаимодействия. Как это обычно бывает при вторичном квантовании, классическое поле Конфигурация вторично квантованной теории задается волновой функцией исходной теории. В случае теории поля струн это означает, что классическая конфигурация, обычно называемая строковое поле, задается элементом свободной строки Пространство фока.

Основные преимущества формализма заключаются в том, что он позволяет вычислять вне оболочки амплитуды и, когда доступно классическое действие, дает непертурбативную информацию, которую нельзя увидеть непосредственно из стандартного разложения по родам струнного рассеяния. В частности, следя за работой Ашоке Сен,^[1] это было полезно при изучении тахионная конденсация на нестабильном D-браны. Он также имел приложения для топологическая теория струн,^[2] некоммутативная геометрия,^[3] и струны малых размеров.^[4]

Теории строкового поля бывают разных видов в зависимости от того, какой тип строки подвергается вторичному квантованию: Теории открытого струнного поля описывают рассеяние открытых струн, теории закрытых струнных полей описывают закрытые строки, а открытые-закрытые струнные теории поля включать как открытые, так и закрытые строки.

Кроме того, в зависимости от метода, используемого для исправления мирового листа диффеоморфизмы и конформные преобразования В исходной теории свободных струн результирующие теории поля струн могут быть самыми разными. С помощью световой конус, дает теории поля струны светового конуса тогда как использование BRST квантование, можно найти ковариантные теории поля струн. Существуют также гибридные теории поля струн, известные как ковариантные теории поля струн светового конуса в которых используются элементы теории поля светового конуса и теории поля струн с фиксированной калибровкой БРСТ.^[5]

Последняя форма теории поля струн, известная как теория поля открытой струны, независимая от фонапринимает совершенно иную форму; вместо вторичного квантования теории струн мирового листа, она вторично квантует пространство двумерных квантовых теорий поля.^[6]

Теория поля струн светового конуса

Теории поля струны светового конуса были введены Стэнли Мандельштам^[7][8] и разработан Мандельштамом, Майкл Грин, Джон Шварц и Ларс Бринк.^{[9][10][11][12][13]} Явное описание вторичного квантования струны светового конуса было дано Мичио Каку и Кейджи Киккава.^[14][15]

Теории поля струны светового конуса были первыми теориями поля струны, которые были построены и основаны на простоте струнного рассеяния в калибровке светового конуса. Например, в бозонная замкнутая струна В этом случае диаграммы рассеяния на мировом листе естественным образом принимают форму диаграммы Фейнмана, состоящую из двух компонентов: пропагатор,

и две вершины для разделения и соединения строк, которые можно использовать для склеивания трех пропагаторов вместе,

Эти вершины и пропагаторы образуют единое покрытие пространства модулей ${\displaystyle n}$-точечные амплитуды рассеяния замкнутой струны, поэтому вершины более высокого порядка не требуются.^[16] Подобные вершины существуют для открытой струны.

Если рассматривать квантование светового конуса суперструныобсуждение более тонкое, поскольку при столкновении вершин светового конуса могут возникнуть расхождения.^[17] Чтобы создать непротиворечивую теорию, необходимо ввести вершины более высокого порядка, называемые контактными членами, чтобы сократить расходимости.

Теории поля светового конуса имеют тот недостаток, что Лоренц-инвариантность. Однако на фоне светоподобный убивающие векторы, они могут значительно упростить квантование струнного действия. Тем более что до появления струны Берковиц^[18] это был единственный известный метод квантования струн в присутствии Рамон-Рамонские поля. В недавних исследованиях теория поля струн светового конуса сыграла важную роль в понимании струн на фоне pp-волн.^[19]

Свободная ковариантная теория поля струн

Важный шаг в построении ковариантных теорий струнного поля (сохраняя манифест Лоренц-инвариантность ) было построением ковариантного кинетического члена. Этот кинетический термин можно рассматривать как самостоятельную теорию поля струн: струнно-полевую теорию свободных струн. Начиная с работы Уоррена Сигела,^[20] это было стандартом для первый BRST-квантование теории свободных струн и тогда выполнить второе квантование, чтобы классические поля теории поля струн включали как призраков, так и поля материи. Например, в случае бозонной теории открытой струны в 26-мерном плоском пространстве-времени общий элемент фоковского пространства БРСТ-квантованной струны принимает вид (при радиальном квантовании в верхней полуплоскости)

${\displaystyle |\Psi \rangle =\int d^{26}p\left(T(p)c_{1}e^{ip\cdot X}|0\rangle +A_{\mu }(p)\partial X^{\mu }c_{1}e^{ip\cdot X}|0\rangle +\chi (p)c_{0}e^{ip\cdot X}|0\rangle +\ldots \right),}$

куда ${\displaystyle |0\rangle }$ - свободный струнный вакуум, а точки представляют собой более массивные поля. На языке теории струн мирового листа ${\displaystyle T(p)}$, ${\displaystyle A_{\mu }(p)}$, и ${\displaystyle \chi (p)}$ представляют собой амплитуды струны, находящейся в различных базисных состояниях. После второго квантования они интерпретируются как классические поля, представляющие тахионный ${\displaystyle T}$, калибровочное поле ${\displaystyle A_{\mu }}$ и призрачное поле ${\displaystyle \chi }$.

В теории струн на мировом листе нефизические элементы пространства Фока удаляются путем наложения условия ${\displaystyle Q_{B}|\Psi \rangle =0}$ а также отношение эквивалентности ${\displaystyle |\Psi \rangle \sim |\Psi \rangle +Q_{B}|\Lambda \rangle }$. После вторичного квантования отношение эквивалентности интерпретируется как калибровочная инвариантность, а условие, что ${\displaystyle |\Psi \rangle }$ физический интерпретируется как уравнение движения. Поскольку физические поля находятся под призрачным номером один, также предполагается, что строковое поле ${\displaystyle |\Psi \rangle }$ является призрачным номером один элемент пространства Фока.

В случае открытой бозонной струны калибровочно-незафиксированное действие с соответствующими симметриями и уравнениями движения было первоначально получено Андре Невё, Герман Николай и Питер К. Уэст.^[21] Это дается

${\displaystyle S_{\text{free open}}(\Psi )={\tfrac {1}{2}}\langle \Psi |Q_{B}|\Psi \rangle \ ,}$

куда ${\displaystyle \langle \Psi |}$ это БПЗ -двойной ${\displaystyle |\Psi \rangle }$.^[22]

Для бозонной замкнутой струны построение БРСТ-инвариантного кинетического члена требует дополнительно наложения ${\displaystyle (L_{0}-{\tilde {L}}_{0})|\Psi \rangle =0}$ и ${\displaystyle (b_{0}-{\tilde {b}}_{0})|\Psi \rangle =0}$. Кинетический член тогда

${\displaystyle S_{\text{free closed}}={\tfrac {1}{2}}\langle \Psi |(c_{0}-{\tilde {c}}_{0})Q_{B}|\Psi \rangle \ .}$

Чтобы суперструны имели дело с нулевыми модами супервуков, необходимы дополнительные соображения.

Кубическая теория поля открытой струны Виттена

Наиболее изученная и простейшая из ковариантных теорий взаимодействующего струнного поля была построена Эдвард Виттен.^[23] Он описывает динамику бозонных открытых струн и задается добавлением к свободному действию открытой струны кубической вершины:

${\displaystyle S(\Psi )={\tfrac {1}{2}}\langle \Psi |Q_{B}|\Psi \rangle +{\tfrac {1}{3}}\langle \Psi ,\Psi ,\Psi \rangle }$,

где, как и в свободном случае, ${\displaystyle \Psi }$ является призрачным элементом номер один в BRST-квантованном свободном бозонном фоковском пространстве с открытой струной.

Кубическая вершина,

${\displaystyle \langle \Psi _{1},\Psi _{2},\Psi _{3}\rangle }$

представляет собой трилинейную карту, которая берет три строковых поля из общего числа призрачных чисел три и дает число. Следуя Виттену, который руководствовался идеями некоммутативной геометрии, принято вводить ${\displaystyle *}$-продукт определен неявно через

${\displaystyle \langle \Sigma |\Psi _{1}*\Psi _{2}\rangle =\langle \Sigma ,\Psi _{1},\Psi _{2}\rangle \ .}$

В ${\displaystyle *}$-произведение и кубическая вершина удовлетворяют ряду важных свойств (позволяющих ${\displaystyle \Psi _{i}}$ быть общими полями числа призраков):

1. Цикличность :

   ${\displaystyle \langle \Psi _{1},\Psi _{2},\Psi _{3}\rangle =(-1)^{gn(\Psi _{3})*(gn(\Psi _{2})+gn(\Psi _{1}))}\langle \Psi _{3},\Psi _{1},\Psi _{2}\rangle }$

2. BRST-инвариантность :
   ${\displaystyle Q_{B}\langle \Psi _{1},\Psi _{2},\Psi _{3}\rangle =\langle Q_{B}\Psi _{1},\Psi _{2},\Psi _{3}\rangle +(-1)^{gn(\Psi _{1})}\langle \Psi _{1},Q_{B}\Psi _{2},\Psi _{3}\rangle +(-1)^{gn(\Psi _{1})+gn(\Psi _{2})}\langle \Psi _{1},\Psi _{2},Q_{B}\Psi _{3}\rangle }$

   Для ${\displaystyle *}$-продукт, это означает, что ${\displaystyle Q_{B}}$ действует как дифференцированный вывод

   ${\displaystyle Q_{B}(\Psi _{1}*\Psi _{2})=(Q_{B}\Psi _{1})*\Psi _{2}+(-1)^{gn(\Psi _{1})}\Psi _{1}*(Q_{B}\Psi _{2})}$

3. Ассоциативность

   ${\displaystyle \left(\Psi _{1}*\Psi _{2}\right)*\Psi _{3}=\Psi _{1}*(\Psi _{2}*\Psi _{3})}$

   В терминах кубической вершины

   ${\displaystyle \langle \Psi _{1},\Psi _{2}*\Psi _{3},\Psi _{4}\rangle =\langle \Psi _{1},\Psi _{2},\Psi _{3}*\Psi _{4}\rangle }$

В этих уравнениях ${\displaystyle gn(\Psi )}$ обозначает призрачное число ${\displaystyle \Psi }$.

Калибровочная инвариантность

Этих свойств кубической вершины достаточно, чтобы показать, что ${\displaystyle S(\Psi )}$ инвариантен относительно Ян – Миллс -подобное калибровочное преобразование,

${\displaystyle \Psi \to \Psi +Q_{B}\Lambda +\Psi *\Lambda -\Lambda *\Psi \ ,}$

куда ${\displaystyle \Lambda }$ - бесконечно малый калибровочный параметр. Конечные калибровочные преобразования принимают вид

${\displaystyle \Psi \to e^{-\Lambda }(\Psi +Q_{B})e^{\Lambda }}$

где экспонента определяется как

${\displaystyle e^{\Lambda }=1+\Lambda +{\tfrac {1}{2}}\Lambda *\Lambda +{\tfrac {1}{3!}}\Lambda *\Lambda *\Lambda +\ldots }$

Уравнения движения

Уравнения движения задаются следующим уравнением:

${\displaystyle Q_{B}\Psi +\Psi *\Psi =0\left.\right.\ .}$

Поскольку строковое поле ${\displaystyle \Psi }$ представляет собой бесконечный набор обычных классических полей, эти уравнения представляют собой бесконечный набор нелинейных связанных дифференциальных уравнений. Было два подхода к поиску решений: во-первых, численно можно усечь строковое поле, чтобы включить только поля с массой меньше фиксированной границы, процедура известна как «усечение уровня».^[24] Это сводит уравнения движения к конечному числу связанных дифференциальных уравнений и привело к открытию многих решений.^[25][26] Во-вторых, вслед за Мартином Шнаблем ^[27] можно искать аналитические решения, тщательно выбирая анзац, который имеет простое поведение при умножении звезды и действии оператора BRST. Это привело к решениям, представляющим предельные деформации, тахионное вакуумное решение^[28] и не зависящие от времени системы D-бран.^[29]

Квантование

Чтобы последовательно квантовать ${\displaystyle S(\Psi )}$ нужно установить датчик. Традиционным выбором была калибровка Фейнмана – Зигеля,

${\displaystyle b_{0}\Psi =0\left.\right.\ .}$

Поскольку калибровочные преобразования сами по себе избыточны (существуют калибровочные преобразования калибровочных преобразований), процедура фиксации калибровки требует введения бесконечного количества призраков через BV формализм.^[30] Полное фиксированное действие калибровки дается выражением

${\displaystyle S_{\text{gauge-fixed}}={\tfrac {1}{2}}\langle \Psi |c_{0}L_{0}|\Psi \rangle +{\tfrac {1}{3}}\langle \Psi ,\Psi ,\Psi \rangle \ ,}$

где поле ${\displaystyle \Psi }$ теперь разрешено быть из произвольное число призраков. В этой шкале Диаграммы Фейнмана построены из одного пропагатора и вершины. Пропагатор представляет собой полосу мирового листа шириной ${\displaystyle \pi }$ и длина ${\displaystyle T}$

Также есть вставка интеграла от ${\displaystyle b}$-призрак вдоль красной линии. Модуль, ${\displaystyle T}$ интегрируется от 0 до ${\displaystyle \infty }$.

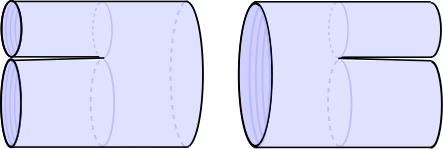
Три вершины можно описать как способ склеивания трех пропагаторов вместе, как показано на следующем рисунке:

Чтобы представить вершину, вложенную в трехмерное изображение, пропагаторы были сложены пополам по их средним точкам. Результирующая геометрия является полностью плоской, за исключением единственной сингулярности кривизны, где встречаются середины трех пропагаторов.

Эти диаграммы Фейнмана генерируют полное покрытие пространства модулей диаграмм рассеяния на открытой струне. Отсюда следует, что для амплитуд на оболочке пАмплитуды открытой струны в точках, вычисленные с использованием теории поля открытой струны Виттена, идентичны амплитудам, вычисленным с использованием стандартных методов мировой таблицы.^[31][32]

Суперсимметричные ковариантные теории поля открытой струны

Есть две основные конструкции суперсимметричный расширения теории поля кубической открытой струны Виттена. Первый очень похож по форме на своего бозонного кузена и известен как модифицированная кубическая теория поля суперструн. Второй из-за Натан Берковиц очень отличается и основан на WZW -тип действия.

Модифицированная кубическая теория поля суперструн

Первое последовательное расширение теории поля бозонной открытой струны Виттена на струну RNS было построено Кристианом Прейтчопфом, Чарльз Торн и Скотт Йост и независимо Ириной Арефьевой, П. Б. Медведевым и А. П. Зубаревым.^[33][34] Поле строки NS считается полем нулевой строки изображения с призрачным номером один в маленьком гильбертовом пространстве (т. Е. ${\displaystyle \eta _{0}|\Psi \rangle =0}$). Действие очень похоже на бозонное действие,

${\displaystyle S(\Psi )={\tfrac {1}{2}}\langle \Psi |Y(i)Y(-i)Q_{B}|\Psi \rangle +{\tfrac {1}{3}}\langle \Psi |Y(i)Y(-i)|\Psi *\Psi \rangle \ ,}$

куда,

${\displaystyle Y(z)=-\partial \xi e^{-2\phi }c(z)}$

- оператор обратного изменения картинки. Предлагаемый ${\displaystyle -{\tfrac {1}{2}}}$ Распространение этой теории числа изображений на сектор Рамона может быть проблематичным.

Было показано, что это действие воспроизводит амплитуды на трех уровнях и имеет тахионное вакуумное решение с правильной энергией.^[35] Единственная тонкость в действии - это вставка операторов, изменяющих картинку в середине, что подразумевает, что линеаризованные уравнения движения принимают форму

${\displaystyle Y(i)Y(-i)Q_{B}\Psi =0\left.\right.\ .}$

Потому что ${\displaystyle Y(i)Y(-i)}$ имеет нетривиальное ядро, есть потенциально дополнительные решения, которые не входят в когомологии ${\displaystyle Q_{B}}$.^[36] Однако такие решения будут содержать операторные вставки около середины и будут потенциально сингулярными, и важность этой проблемы остается неясной.

Теория поля суперструн Берковица

Совершенно иное суперсимметричное действие для открытой струны было построено Натаном Берковицем. Это принимает форму^[37]

${\displaystyle S={\tfrac {1}{2}}\langle e^{-\Phi }Q_{B}e^{\Phi }|e^{-\Phi }\eta _{0}e^{\Phi }\rangle -{\tfrac {1}{2}}\int _{0}^{1}dt\langle e^{-{\hat {\Phi }}}\partial _{t}e^{\hat {\Phi }}|\{e^{-{\hat {\Phi }}}Q_{B}e^{\hat {\Phi }},e^{-{\hat {\Phi }}}\eta _{0}e^{\hat {\Phi }}\}\rangle }$

где все продукты выполняются с использованием ${\displaystyle *}$-продукт, включающий антикоммутатор ${\displaystyle \{,\}}$, и ${\displaystyle {\hat {\Phi }}(t)}$ любое строковое поле такое, что ${\displaystyle {\hat {\Phi }}(0)=0}$ и ${\displaystyle {\hat {\Phi }}(1)=\Phi }$. Строковое поле ${\displaystyle \Phi }$ считается лежащим в NS-секторе большого гильбертова пространства, т. е. включая нулевой режим ${\displaystyle \xi }$. Неизвестно, как включить сектор R, хотя есть некоторые предварительные идеи.^[38]

Уравнения движения принимают вид

${\displaystyle \eta _{0}\left(e^{-\Phi }Q_{B}e^{\Phi }\right)=0.}$

Действие инвариантно относительно калибровочного преобразования

${\displaystyle e^{\Phi }\to e^{Q_{B}\Lambda }e^{\Phi }e^{\eta _{0}\Lambda '}.}$

Основным преимуществом этого действия является то, что в нем отсутствуют какие-либо вставки операторов, изменяющих изображение. Было показано, что правильно воспроизводятся амплитуды на уровне деревьев.^[39] и численно было обнаружено, что он имеет тахионный вакуум с соответствующей энергией.^[40][41] К известным аналитическим решениям классических уравнений движения относится тахионный вакуум^[42] и предельные деформации.

Другие формулировки ковариантной теории поля открытых суперструн

Формулировка теории поля суперструн с использованием неминимальных чисто спинорных переменных была введена Берковицем.^[43] Действие является кубическим и включает вставку средней точки, ядро ​​которой тривиально. Как всегда в случае чистых спиноров, сектор Рамон легко поддается лечению. Однако неизвестно, как включить в формализм GSO-секторы.

В попытке разрешить якобы проблематичную вставку средней точки модифицированной кубической теории Берковиц и Зигель предложили теорию поля суперструн, основанную на неминимальном расширении струны RNS,^[44] который использует вставку средней точки без ядра. Неясно, лучше ли такие вставки, чем вставки средней точки с нетривиальными ядрами.

Ковариантная теория поля замкнутой струны

Ковариантные теории поля с замкнутой струной значительно сложнее, чем их собратья с открытой струной. Даже если кто-то хочет построить теорию поля струн, которая только воспроизводит древовидный взаимодействия между замкнутыми струнами, классическое действие должно содержать бесконечный количество вершин ^[45] состоящий из струнных многогранников.^[46][47]

Если кто-то требует, чтобы диаграммы рассеяния на оболочке воспроизводились для всех порядков сцепления струн, необходимо также включить дополнительные вершины, возникающие из более высокого рода (и, следовательно, более высокого порядка по ${\displaystyle \hbar }$) также. В общем случае явно BV-инвариантное квантованное действие принимает вид^[48]

${\displaystyle S(\Psi )=\hbar \sum _{g\geq 0}(\hbar g_{c})^{g-1}\sum _{n\geq 0}{\frac {1}{n!}}\{\Psi ^{n}\}_{g}}$

куда ${\displaystyle \{\Psi ^{n}\}_{g}}$ обозначает ${\displaystyle n}$вершина-го порядка, возникающая из рода ${\displaystyle g}$ поверхность и ${\displaystyle g_{c}}$ - замкнутая струнная муфта. Структура вершин в принципе определяется предписанием минимальной площади,^[49] хотя даже для многогранных вершин явные вычисления были выполнены только до пятого порядка.^[50][51]

Ковариантная гетеротическая теория поля струн

Формулировка NS-сектора гетеротической струны была дана Берковицем, Окавой и Цвибахом.^[52]Эта формулировка объединяет бозонную теорию поля замкнутых струн с теорией поля суперструн Берковица.

Смотрите также

• Конформная теория поля
• F-теория
• Fuzzballs
• Список тем теории струн
• Маленькая теория струн
• Петлевая квантовая гравитация
• Связь теории струн и квантовой теории поля
• Струнная космология
• Супергравитация
• Элегантная Вселенная
• Регуляризация дзета-функции

Рекомендации

1. Сен, Ашок (1999-12-29). «Универсальность тахионного потенциала». Журнал физики высоких энергий. 1999 (12): 027. arXiv:hep-th / 9911116. Bibcode:1999JHEP ... 12..027S. Дои:10.1088/1126-6708/1999/12/027. ISSN  1029-8479.
2. Э. Виттен, "Калибровочная теория Черна – Саймонса как теория струн", Prog. Математика. 133 637, (1995)
3. Э. Виттен, "Некоммутативные тахионы и теория поля струн", hep-th / 0006071
4. Гайотто, Давиде; Растелли, Леонардо (25 июля 2005 г.). «Парадигма открытой / закрытой двойственности Лиувиллевских D-бран и модель Концевича». Журнал физики высоких энергий. 2005 (7): 053. arXiv:hep-th / 0312196. Bibcode:2005JHEP ... 07..053G. Дои:10.1088/1126-6708/2005/07/053. ISSN  1029-8479.
5. Хата, Хироюки; Ито, Кацуми; Куго, Тайчиро; Кунитомо, Хироши; Огава, Каку (1986). «Явно ковариантная теория поля взаимодействующей струны I». Письма по физике B. Elsevier BV. 172 (2): 186–194. Bibcode:1986ФЛБ..172..186Х. Дои:10.1016/0370-2693(86)90834-8. ISSN  0370-2693.
6. Виттен, Эдвард (1992-12-15). «О теории поля открытой струны, не зависящей от фона». Физический обзор D. 46 (12): 5467–5473. arXiv:hep-th / 9208027. Bibcode:1992ПхРвД..46.5467Вт. Дои:10.1103 / Physrevd.46.5467. ISSN  0556-2821. PMID  10014938.
7. Мандельштам, С. (1973). «Картина взаимодействующих струн моделей двойного резонанса». Ядерная физика B. Elsevier BV. 64: 205–235. Bibcode:1973НуФБ..64..205М. Дои:10.1016/0550-3213(73)90622-6. ISSN  0550-3213.
8. Мандельштам, С. (1974). "Взаимодействующая струнная картина модели Невё-Шварца-Рамона". Ядерная физика B. Elsevier BV. 69 (1): 77–106. Bibcode:1974НуФБ..69 ... 77М. Дои:10.1016/0550-3213(74)90127-8. ISSN  0550-3213.
9. Грин, Майкл Б .; Шварц, Джон Х. (1982). «Суперсимметричная дуальная теория струн: (II). Вершины и деревья». Ядерная физика B. Elsevier BV. 198 (2): 252–268. Bibcode:1982НуФБ.198..252Г. Дои:10.1016/0550-3213(82)90556-9. ISSN  0550-3213.
10. Грин, Майкл Б .; Шварц, Джон Х. (1983). «Суперструнные взаимодействия». Ядерная физика B. Elsevier BV. 218 (1): 43–88. Bibcode:1983НуФБ.218 ... 43Г. Дои:10.1016/0550-3213(83)90475-3. ISSN  0550-3213.
11. Грин, Майкл Б .; Шварц, Джон Х .; Бринк, Ларс (1983). «Суперполевая теория суперструн типа (II)». Ядерная физика B. Elsevier BV. 219 (2): 437–478. Bibcode:1983НуФБ.219..437Г. Дои:10.1016 / 0550-3213 (83) 90651-х. ISSN  0550-3213.
12. Грин, Майкл Б .; Шварц, Джон Х. (1984). "Теория поля суперструн". Ядерная физика B. Elsevier BV. 243 (3): 475–536. Bibcode:1984НуФБ.243..475Г. Дои:10.1016/0550-3213(84)90488-7. ISSN  0550-3213.
13. Мандельштам, Стэнли (1986). "Картина взаимодействующей струны фермионной струны". Приложение "Прогресс теоретической физики". Издательство Оксфордского университета (ОУП). 86: 163–170. Bibcode:1986ПТПС..86..163М. Дои:10.1143 / ptps.86.163. ISSN  0375-9687.
14. Каку, Мичио; Киккава, К. (1974-08-15). «Полевая теория релятивистских струн. I. Деревья». Физический обзор D. Американское физическое общество (APS). 10 (4): 1110–1133. Bibcode:1974ПхРвД..10.1110К. Дои:10.1103 / Physrevd.10.1110. ISSN  0556-2821.
15. Каку, Мичио; Киккава, К. (1974-09-15). «Полевая теория релятивистских струн. II. Петли и помероны». Физический обзор D. Американское физическое общество (APS). 10 (6): 1823–1843. Bibcode:1974ПхРвД..10.1823К. Дои:10.1103 / Physrevd.10.1823. ISSN  0556-2821.
16. Д'Хокер, Эрик; Гиддингс, Стивен Б. (1987). «Унитарность замкнутой бозонной струны Полякова». Ядерная физика B. Elsevier BV. 291: 90–112. Bibcode:1987НуФБ.291 ... 90Д. Дои:10.1016/0550-3213(87)90466-4. ISSN  0550-3213.
17. Greensite, J .; Клинкхамер, Ф. (1987). «Новые взаимодействия суперструн». Ядерная физика B. Elsevier BV. 281 (1–2): 269–288. Bibcode:1987НуФБ.281..269Г. Дои:10.1016/0550-3213(87)90256-2. ISSN  0550-3213.
18. Берковиц, Натан (2000-04-15). «Ковариантное квантование супер-Пуанкаре суперструны». Журнал физики высоких энергий. 2000 (4): 018. arXiv:hep-th / 0001035. Bibcode:2000JHEP ... 04..018B. Дои:10.1088/1126-6708/2000/04/018. ISSN  1029-8479.
19. М. Спрадлин и А. Волович, "Теория поля струны на световом конусе в плоской волне", Лекции, прочитанные в Весенней школе ICTP по теории суперструн и смежным темам, Триест, Италия, 31 марта - 8 апреля (2003 г.) hep-th / 0310033.
20. В. Сигел, "Теория поля струн через BRST", в Санта-Барбаре, 1985, Proceedings, Unified String Theories, 593;
    W. Siegel, "Введение в теорию поля струн", Adv. Сер. Математика. Phys. 8. Перепечатано как hep-th / 0107094
21. Neveu, A .; Nicolai, H .; Уэст, П. (1986). «Новые симметрии и призрачная структура ковариантных теорий струн». Письма по физике B. Elsevier BV. 167 (3): 307–314. Bibcode:1986ФЛБ..167..307Н. Дои:10.1016/0370-2693(86)90351-5. ISSN  0370-2693.
22. Белавин, А.А .; Поляков, А.М .; Замолодчиков, А. (1984). «Бесконечная конформная симметрия в двумерной квантовой теории поля». Ядерная физика B. Elsevier BV. 241 (2): 333–380. Bibcode:1984НуФБ.241..333Б. Дои:10.1016 / 0550-3213 (84) 90052-х. ISSN  0550-3213.
23. Виттен, Эдвард (1986). «Некоммутативная геометрия и теория поля струн». Ядерная физика B. Elsevier BV. 268 (2): 253–294. Bibcode:1986НуФБ.268..253Вт. Дои:10.1016/0550-3213(86)90155-0. ISSN  0550-3213.
24. Костелецкий, В. Алан; Сэмюэл, Стюарт (1989-01-15). «Самопроизвольное нарушение лоренцевой симметрии в теории струн». Физический обзор D. Американское физическое общество (APS). 39 (2): 683–685. Bibcode:1989ПхРвД..39..683К. Дои:10.1103 / Physrevd.39.683. HDL:2022/18649. ISSN  0556-2821.
25. Цвибах, Бартон (2001). «Достаточно ли большого струнного поля?». Fortschritte der Physik. Вайли. 49 (4–6): 387. Bibcode:2001ForPh..49..387Z. Дои:10.1002 / 1521-3978 (200105) 49: 4/6 <387 :: aid-prop387> 3.0.co; 2-z. ISSN  0015-8208.
26. Тейлор, Вашингтон; Цвибах, Бартон (2004). D-Бран, тахионы и теория поля струн. World Scientific. С. 641–670. arXiv:hep-th / 0311017. Дои:10.1142/9789812702821_0012. ISBN  978-981-238-788-2.
27. Шнабль, Мартин (2006). «Аналитическое решение для тахионной конденсации в теории поля открытой струны». Успехи теоретической и математической физики. 10 (4): 433–501. arXiv:hep-th / 0511286. Дои:10.4310 / atmp.2006.v10.n4.a1. ISSN  1095-0761.
28. Фукс, Эхуд; Кройтер, Майкл (2011). «Аналитические решения теории поля открытой струны». Отчеты по физике. 502 (4–5): 89–149. arXiv:0807.4722. Bibcode:2011ФР ... 502 ... 89Ф. Дои:10.1016 / j.physrep.2011.01.003. ISSN  0370-1573.
29. Эрлер, Теодор; Маккаферри, Карло (2014). «Решение теории поля струн для любого открытого струнного фона». Журнал физики высоких энергий. Springer Nature. 2014 (10): 029. arXiv:1406.3021. Bibcode:2014JHEP ... 10..029E. Дои:10.1007 / jhep10 (2014) 029. ISSN  1029-8479.
30. Торн, Чарльз Б. (1989). «Теория струнного поля». Отчеты по физике. Elsevier BV. 175 (1–2): 1–101. Bibcode:1989ФР ... 175 .... 1Т. Дои:10.1016 / 0370-1573 (89) 90015-х. ISSN  0370-1573.
31. Гиддингс, Стивен Б.; Мартинек, Эмиль; Виттен, Эдвард (1986). «Модулярная инвариантность в теории поля струн». Письма по физике B. Elsevier BV. 176 (3–4): 362–368. Bibcode:1986ФЛБ..176..362Г. Дои:10.1016/0370-2693(86)90179-6. ISSN  0370-2693.
32. Цвибах, Бартон (1991). «Доказательство того, что открытая теория струн Виттена дает единственное покрытие пространства модулей». Коммуникации по математической физике. ООО "Спрингер Сайенс энд Бизнес Медиа". 142 (1): 193–216. Bibcode:1991CMaPh.142..193Z. Дои:10.1007 / bf02099176. ISSN  0010-3616.
33. Preitschopf, Christian R .; Thorn, Charles B .; Йост, Скотт (1990). "Теория поля суперструн". Ядерная физика B. Elsevier BV. 337 (2): 363–433. Bibcode:1990НуФБ.337..363П. Дои:10.1016 / 0550-3213 (90) 90276-к. ISSN  0550-3213.
34. Арефьева И.Я .; Медведев, П.Б .; Зубарев, А.П. (1990). «Новое представление для поля струны решает проблему согласованности теории поля открытой суперструны». Ядерная физика B. Elsevier BV. 341 (2): 464–498. Bibcode:1990НуФБ.341..464А. Дои:10.1016 / 0550-3213 (90) 90189-к. ISSN  0550-3213.
35. Эрлер, Теодор (2007-01-07). «Тахионный вакуум в кубической теории поля суперструн». Журнал физики высоких энергий. 2008 (1): 013. arXiv:0707.4591. Bibcode:2008JHEP ... 01..013E. Дои:10.1088/1126-6708/2008/01/013. ISSN  1029-8479.
36. Н. Берковиц, "Обзор теории поля открытых суперструн", hep-th / 0105230
37. Берковиц, Натан (1995). "Супер-Пуанкаре-инвариантная теория поля суперструн". Ядерная физика B. Elsevier BV. 450 (1–2): 90–102. arXiv:hep-th / 9503099. Bibcode:1995НуФБ.450 ... 90Б. Дои:10.1016 / 0550-3213 (95) 00259-у. ISSN  0550-3213.
38. Мичисита, Йоджи (7 января 2005 г.). "Ковариантное действие с ограничением и правилами Фейнмана для фермионов в открытой теории поля суперструн". Журнал физики высоких энергий. 2005 (1): 012. arXiv:hep-th / 0412215. Bibcode:2005JHEP ... 01..012M. Дои:10.1088/1126-6708/2005/01/012. ISSN  1029-8479.
39. Берковиц, Натан; Эчеваррия, Карлос Тельо (2000). «Четырехточечная амплитуда из теории поля открытой суперструны». Письма по физике B. Elsevier BV. 478 (1–3): 343–350. arXiv:hep-th / 9912120. Bibcode:2000ФЛБ..478..343Б. Дои:10.1016 / с0370-2693 (00) 00246-х. ISSN  0370-2693.
40. Берковиц, Натан (2000-04-19). «Тахионный потенциал в открытой теории поля струн Невё-Шварца». Журнал физики высоких энергий. 2000 (4): 022. arXiv:hep-th / 0001084. Bibcode:2000JHEP ... 04..022B. Дои:10.1088/1126-6708/2000/04/022. ISSN  1029-8479.
41. Берковиц, Натан; Сен, Ашок; Цвибах, Бартон (2000). «Тахионная конденсация в теории поля суперструн». Ядерная физика B. 587 (1–3): 147–178. arXiv:hep-th / 0002211. Bibcode:2000НуФБ.587..147Б. Дои:10.1016 / s0550-3213 (00) 00501-0. ISSN  0550-3213.
42. Эрлер, Теодор (2013). «Аналитическое решение для тахионной конденсации в открытой теории поля суперструн Берковица». Журнал физики высоких энергий. 2013 (11): 7. arXiv:1308.4400. Bibcode:2013JHEP ... 11..007E. Дои:10.1007 / jhep11 (2013) 007. ISSN  1029-8479.
43. Берковиц, Натан (2005-10-27). «Чистый спинорный формализм как топологическая струна N = 2». Журнал физики высоких энергий. 2005 (10): 089. arXiv:hep-th / 0509120. Bibcode:2005JHEP ... 10..089B. Дои:10.1088/1126-6708/2005/10/089. ISSN  1029-8479.
44. Берковиц, Натан; Сигел, Уоррен (2009-11-05). "Регуляризация кубической открытой теории поля струн Невё-Шварца". Журнал физики высоких энергий. 2009 (11): 021. arXiv:0901.3386. Bibcode:2009JHEP ... 11..021B. Дои:10.1088/1126-6708/2009/11/021. ISSN  1029-8479.
45. Сонода, Хиденори; Цвибах, Бартон (1990). «Ковариантная замкнутая теория струн не может быть кубической». Ядерная физика B. Elsevier BV. 336 (2): 185–221. Bibcode:1990НуФБ.336..185С. Дои:10.1016 / 0550-3213 (90) 90108-п. ISSN  0550-3213.
46. Саади, Маха; Цвибах, Бартон (1989). "Теория поля замкнутой струны из многогранников". Анналы физики. Elsevier BV. 192 (1): 213–227. Bibcode:1989АнФи.192..213С. Дои:10.1016/0003-4916(89)90126-7. ISSN  0003-4916.
47. Куго, Тайчиро; Суэхиро, Казухиро (1990). «Неполиномиальная замкнутая теория поля струны: действие и его калибровочная инвариантность». Ядерная физика B. Elsevier BV. 337 (2): 434–466. Bibcode:1990НуФБ.337..434К. Дои:10.1016 / 0550-3213 (90) 90277-к. ISSN  0550-3213.
48. Цвибах, Бартон (1993). "Теория поля замкнутой струны: квантовое действие и главное уравнение Баталина-Вилковиского". Ядерная физика B. 390 (1): 33–152. arXiv:hep-th / 9206084. Bibcode:1993НуФБ.390 ... 33З. Дои:10.1016/0550-3213(93)90388-6. ISSN  0550-3213.
49. Цвибах, Бартон (1990-12-30). «Квантовые замкнутые струны с минимальной площади». Буквы A по современной физике. World Scientific Pub Co Pte Lt. 05 (32): 2753–2762. Bibcode:1990MPLA .... 5.2753Z. Дои:10.1142 / s0217732390003218. ISSN  0217-7323.
50. Мёллер, Николас (12 марта 2007 г.). «Теория поля замкнутой бозонной струны в пятом порядке: контактный член с пятью тахионами и теорема о дилатоне». Журнал физики высоких энергий. 2007 (3): 043. arXiv:hep-th / 0609209. Bibcode:2007JHEP ... 03..043M. Дои:10.1088/1126-6708/2007/03/043. ISSN  1029-8479.
51. Мёллер, Николас (26 сентября 2007 г.). «Теория поля замкнутой бозонной струны пятого порядка II: маргинальные деформации и эффективный потенциал». Журнал физики высоких энергий. 2007 (9): 118. arXiv:0705.2102. Bibcode:2007JHEP ... 09..118M. Дои:10.1088/1126-6708/2007/09/118. ISSN  1029-8479.
52. Берковиц, Натан; Окава, Юдзи; Цвибах, Бартон (2004-11-16). "WZW-подобное действие для теории гетеротического струнного поля". Журнал физики высоких энергий. 2004 (11): 038. arXiv:hep-th / 0409018. Bibcode:2004JHEP ... 11..038B. Дои:10.1088/1126-6708/2004/11/038. ISSN  1029-8479.