Закон Снеллиуса - Snells law

Преломление света на стыке двух сред с разными показатели преломления, с n₂ > п₁. Поскольку во второй среде скорость меньше (v₂ 1) угол преломления θ₂ меньше угла падения θ₁; то есть луч в среде с более высоким индексом ближе к нормальному.

Закон Снеллиуса (также известный как Закон Снеллиуса-Декарта и закон преломления) это формула используется для описания отношений между углы падения и преломление, когда речь идет о свете или другом волны проходя через границу между двумя разными изотропный средства массовой информации, например вода, стакан или воздух.

В оптике закон используется в трассировка лучей для вычисления углов падения или преломления, а в экспериментальной оптике - для определения показатель преломления материала. Закон также выполняется в метаматериалы, которые позволяют свету отклоняться «назад» под отрицательным углом преломления с отрицательный показатель преломления.

Закон Снеллиуса гласит, что отношение синусы углов падения и преломления эквивалентно отношению фазовые скорости в двух средах, или эквивалент, обратный отношению показатели преломления:

${\displaystyle {\frac {\sin \theta _{2}}{\sin \theta _{1}}}={\frac {v_{2}}{v_{1}}}={\frac {n_{1}}{n_{2}}}}$

с каждым ${\displaystyle \theta }$ как угол, отсчитываемый от нормали к границе, ${\displaystyle v}$ как скорость света в соответствующей среде (единицы СИ - метры в секунду или м / с), и ${\displaystyle n}$ как показатель преломления (безразмерный) соответствующей среды.

Закон следует из Ферма с принцип наименьшего времени, что, в свою очередь, следует из распространения света в виде волн.

История

Воспроизведение страницы Ибн Сахл Рукопись, показывающая его открытие закона преломления.

Птолемей, в Александрия, Египет,^[1] обнаружил зависимость относительно углов преломления, но она была неточной для углов, которые не были малыми. Птолемей был уверен, что нашел точный эмпирический закон, частично в результате небольшого изменения своих данных в соответствии с теорией (см.: Подтверждение смещения ).^[2] Альхазен, в его Книга оптики (1021), подошел к открытию закона преломления, хотя и не пошел на этот шаг.^[3]

Взгляд 1837 года на историю "Закона синуса"^[4]

Закон, впоследствии названный в честь Снелла, был впервые точно описан персидским ученым. Ибн Сахл на Багдад суд в 984 году. В рукописи О горящих зеркалах и линзахСаль использовал этот закон для получения формы линз, которые фокусируют свет без геометрических аберраций.^[5]

Закон был открыт заново Томас Харриот в 1602 г.^[6] который, однако, не опубликовал свои результаты, хотя он переписывался с Кеплер на эту самую тему. В 1621 году голландский астроном Виллеброрд Снеллиус (1580–1626) - Снелл - вывел математически эквивалентную форму, которая оставалась неопубликованной при его жизни. Рене Декарт независимо вывел закон, используя эвристические аргументы сохранения импульса в терминах синусов в своем эссе 1637 г. Диоптрика, и использовал его для решения ряда оптических проблем. Отвергая решение Декарта, Пьер де Ферма пришел к такому же решению, основываясь исключительно на его принцип наименьшего времени. Декарт предположил скорость света был бесконечен, но при выводе закона Снеллиуса он также предполагал, что чем плотнее среда, тем больше скорость света. Ферма поддержал противоположные предположения, то есть скорость света конечна, и его вывод зависел от того, что скорость света меньше в более плотной среде.^[7][8] Вывод Ферма также использовал его изобретение адекватность, математическая процедура, эквивалентная дифференциальному исчислению, для нахождения максимумов, минимумов и касательных.^[9][10]

В его влиятельной книге по математике Геометрия, Декарт решает проблему, над которой работал Аполлоний Пергский и Папп Александрийский. Даны n прямых L и точка P (L) на каждой прямой. Найдите геометрическое место точек Q, такое, что длины отрезков QP (L) удовлетворяют определенным условиям. Например, когда n = 4, учитывая прямые a, b, c и d и точку A на a, B на b и т. Д., Найдите геометрическое место точек Q, такое, что произведение QA * QB равно произведению КК * КД. Когда не все прямые параллельны, Папп показал, что локусы являются коническими, но когда Декарт рассмотрел большее n, он получил кубические кривые и кривые более высокой степени. Чтобы показать, что кубические кривые интересны, он показал, что они естественным образом возникли в оптике из закона Снеллиуса.^[11]

По словам Дейкстерхейса,^[12] "В De natura lucis et proprietate (1662) Исаак Воссиус сказал, что Декарт видел статью Снелла и придумал собственное доказательство. Теперь мы знаем, что это обвинение незаслуженно, но с тех пор оно многократно повторялось ». И Ферма, и Гюйгенс повторили обвинение в том, что Декарт скопировал Снелла. Французский Закон Снеллиуса называется «la loi de Descartes» или «loi de Snell-Descartes».

Кристиан Гюйгенс ' строительство

В его 1678 г. Traité de la Lumière, Кристиан Гюйгенс показал, как закон синусов Снеллиуса может быть объяснен или выведен из волновой природы света, используя то, что мы стали называть Принцип Гюйгенса – Френеля.

С развитием современной оптической и электромагнитной теории древний закон Снеллиуса перешел на новую стадию. В 1962 г. Бломберген показал, что на границе нелинейной среды закон Снеллиуса должен быть записан в общем виде.^[13] В 2008 и 2011 гг. плазмонные метаповерхности также было продемонстрировано изменение направлений отражения и преломления светового луча.^[14][15]

Объяснение

Закон Снеллиуса на стене в Лейдене

Закон Снеллиуса используется для определения направления световых лучей через преломляющие среды с различными показателями преломления. Показатели преломления сред, обозначенные ${\displaystyle n_{1}}$, ${\displaystyle n_{2}}$ и так далее, используются для обозначения коэффициента, на который уменьшается скорость светового луча при прохождении через преломляющую среду, такую ​​как стекло или вода, в отличие от его скорости в вакууме.

Когда свет проходит границу между средами, в зависимости от относительных показателей преломления двух сред, свет будет преломляться либо на меньший, либо на больший угол. Эти углы измеряются относительно нормальная линия, представленный перпендикулярно границе. В случае, если свет распространяется из воздуха в воду, свет будет преломляться в направлении нормальной линии, потому что в воде свет замедляется; свет, идущий от воды к воздуху, преломлялся бы от нормальной линии.

Преломление между двумя поверхностями также называют обратимый потому что если бы все условия были идентичны, углы были бы одинаковыми для света, распространяющегося в противоположном направлении.

Закон Снеллиуса обычно справедлив только для изотропных или зеркальных сред (таких как стекло ). В анизотропный СМИ, такие как некоторые кристаллы, двулучепреломление может разбить преломленный луч на два луча, обычный или же о-рей, который следует закону Снеллиуса, а другой необычный или же е-луч, который может не совпадать с падающим лучом.

Когда свет или другая волна является монохроматической, то есть одной частоты, закон Снеллиуса также может быть выражен через отношение длин волн в двух средах: ${\displaystyle \lambda _{1}}$ и ${\displaystyle \lambda _{2}}$:

${\displaystyle {\frac {\sin \theta _{1}}{\sin \theta _{2}}}={\frac {v_{1}}{v_{2}}}={\frac {\lambda _{1}}{\lambda _{2}}}}$

Выводы и формулы

Волновые фронты из точечный источник в контексте закона Снеллиуса. Область ниже серой линии имеет более высокий показатель преломления, и пропорционально ниже скорость света, чем область над ним.

Закон Снеллиуса может быть получен разными способами.

Вывод из принципа Ферма

Закон Снеллиуса может быть получен из Принцип Ферма, который утверждает, что свет проходит путь, который занимает наименьшее время. Взяв производная из длина оптического пути, то стационарный пункт найдено, указывая путь, пройденный светом. (Существуют ситуации, когда свет нарушает принцип Ферма, не выбирая наименьшего временного пути, как при отражении в (сферическом) зеркале.) В классической аналогии область нижнего показатель преломления заменяется пляжем, площадь выше показатель преломления у моря, и самый быстрый способ для спасателя на пляже добраться до тонущий Человек в море должен бежать по тропе, соответствующей закону Снеллиуса.

Свет из среды 1, точка Q, попадает в среду 2, происходит рефракция и, наконец, достигает точки P.

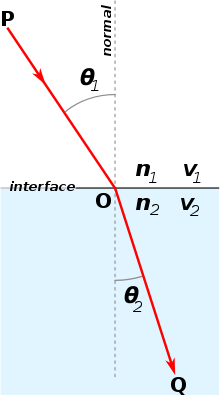
Как показано на рисунке справа, предположим, что показатели преломления среды 1 и среды 2 равны ${\displaystyle n_{1}}$ и ${\displaystyle n_{2}}$ соответственно. Свет входит в среду 2 из среды 1 через точку O.

${\displaystyle \theta _{1}}$ угол падения, ${\displaystyle \theta _{2}}$ - угол преломления относительно нормали.

Фазовые скорости света в среде 1 и среде 2 равны

${\displaystyle v_{1}=c/n_{1}}$ и

${\displaystyle v_{2}=c/n_{2}}$ соответственно.

${\displaystyle c}$ это скорость света в вакууме.

Пусть T - время, необходимое свету, чтобы пройти из точки Q через точку O в точку P.

${\displaystyle T={\frac {\sqrt {x^{2}+a^{2}}}{v_{1}}}+{\frac {\sqrt {b^{2}+(l-x)^{2}}}{v_{2}}}={\frac {\sqrt {x^{2}+a^{2}}}{v_{1}}}+{\frac {\sqrt {b^{2}+l^{2}-2lx+x^{2}}}{v_{2}}}}$

где a, b, l и x обозначены на правом рисунке, где x - изменяющийся параметр.

Чтобы его минимизировать, можно выделить:

${\displaystyle {\frac {dT}{dx}}={\frac {x}{v_{1}{\sqrt {x^{2}+a^{2}}}}}+{\frac {-(l-x)}{v_{2}{\sqrt {(l-x)^{2}+b^{2}}}}}=0}$ (стационарная точка)

Обратите внимание, что${\displaystyle {\frac {x}{\sqrt {x^{2}+a^{2}}}}=\sin \theta _{1}}$

и ${\displaystyle {\frac {l-x}{\sqrt {(l-x)^{2}+b^{2}}}}=\sin \theta _{2}}$

Следовательно,

${\displaystyle {\frac {dT}{dx}}={\frac {\sin \theta _{1}}{v_{1}}}-{\frac {\sin \theta _{2}}{v_{2}}}=0}$

${\displaystyle {\frac {\sin \theta _{1}}{v_{1}}}={\frac {\sin \theta _{2}}{v_{2}}}}$

${\displaystyle {\frac {n_{1}\sin \theta _{1}}{c}}={\frac {n_{2}\sin \theta _{2}}{c}}}$

${\displaystyle n_{1}\sin \theta _{1}=n_{2}\sin \theta _{2}}$

Вывод из принципа Гюйгенса

Дальнейшая информация: Принцип Гюйгенса – Френеля

В качестве альтернативы, закон Снеллиуса может быть получен с использованием интерференции всех возможных путей световой волны от источника к наблюдателю - это приводит к деструктивной интерференции везде, кроме экстремумов фазы (где интерференция конструктивна), которые становятся реальными путями.

Вывод из уравнений Максвелла.

Дальнейшая информация: Уравнения Френеля

Другой способ вывести закон Снеллиуса заключается в применении общего граничные условия из Уравнения Максвелла за электромагнитное излучение.

Вывод из закона сохранения энергии и импульса

Еще один способ вывести закон Снеллиуса основан на соображениях симметрии трансляции.^[16] Например, однородная поверхность, перпендикулярная направлению z, не может изменить поперечный импульс. Поскольку вектор распространения ${\displaystyle {\vec {k}}}$ пропорциональна импульсу фотона, поперечное направление распространения ${\displaystyle (k_{x},k_{y},0)}$ должны оставаться одинаковыми в обоих регионах. Без ограничения общности предположим, что плоскость падения ${\displaystyle z,x}$ самолет ${\displaystyle k_{x{\text{Region}}_{1}}=k_{x{\text{Region}}_{2}}}$. Используя известную зависимость волновое число на показатель преломления среды, мы немедленно выводим закон Снеллиуса.

${\displaystyle k_{x{\text{Region}}_{1}}=k_{x{\text{Region}}_{2}}\,}$

${\displaystyle n_{1}k_{0}\sin \theta _{1}=n_{2}k_{0}\sin \theta _{2}\,}$

${\displaystyle n_{1}\sin \theta _{1}=n_{2}\sin \theta _{2}\,}$

куда ${\displaystyle k_{0}={\frac {2\pi }{\lambda _{0}}}={\frac {\omega }{c}}}$ - волновое число в вакууме. Хотя ни одна поверхность не является по-настоящему однородной в атомном масштабе, полная трансляционная симметрия является отличным приближением, когда область однородна в масштабе длины световой волны.

Векторная форма

Смотрите также: Зеркальное отражение § Направление отражения

Учитывая нормализованный световой вектор ${\displaystyle {\vec {l}}}$ (направленный от источника света к поверхности) и нормализованный вектор нормали плоскости ${\displaystyle {\vec {n}}}$, можно вычислить нормализованные отраженные и преломленные лучи через косинусы угла падения ${\displaystyle \theta _{1}}$ и угол преломления ${\displaystyle \theta _{2}}$, без явного использования значений синуса или каких-либо тригонометрических функций или углов:^[17]

${\displaystyle \cos \theta _{1}=-{\vec {n}}\cdot {\vec {l}}}$

Примечание: ${\displaystyle \cos \theta _{1}}$ должно быть положительным, что будет, если ${\displaystyle {\vec {n}}}$ - вектор нормали, который указывает от поверхности к стороне, откуда исходит свет, область с индексом ${\displaystyle n_{1}}$. Если ${\displaystyle \cos \theta _{1}}$ отрицательно, то ${\displaystyle {\vec {n}}}$ указывает в сторону без света, поэтому начните с ${\displaystyle {\vec {n}}}$ заменен его отрицательным.

${\displaystyle {\vec {v}}_{\mathrm {reflect} }={\vec {l}}+2\cos \theta _{1}{\vec {n}}}$

Этот вектор направления отражения указывает обратно на сторону поверхности, откуда исходит свет.

Теперь примените закон Снеллиуса к соотношению синусов, чтобы получить формулу для вектора направления преломленного луча:

${\displaystyle \sin \theta _{2}=\left({\frac {n_{1}}{n_{2}}}\right)\sin \theta _{1}=\left({\frac {n_{1}}{n_{2}}}\right){\sqrt {1-\left(\cos \theta _{1}\right)^{2}}}}$

${\displaystyle \cos \theta _{2}={\sqrt {1-(\sin \theta _{2})^{2}}}={\sqrt {1-\left({\frac {n_{1}}{n_{2}}}\right)^{2}\left(1-\left(\cos \theta _{1}\right)^{2}\right)}}}$

${\displaystyle {\vec {v}}_{\mathrm {refract} }=\left({\frac {n_{1}}{n_{2}}}\right){\vec {l}}+\left({\frac {n_{1}}{n_{2}}}\cos \theta _{1}-\cos \theta _{2}\right){\vec {n}}}$

Формула может показаться более простой с точки зрения переименованных простых значений ${\displaystyle r=n_{1}/n_{2}}$ и ${\displaystyle c=-{\vec {n}}\cdot {\vec {l}}}$, избегая появления имен триггерных функций или углов:

${\displaystyle {\vec {v}}_{\mathrm {refract} }=r{\vec {l}}+\left(rc-{\sqrt {1-r^{2}\left(1-c^{2}\right)}}\right){\vec {n}}}$

Пример:

${\displaystyle {\vec {l}}=\{0.707107,-0.707107\},~{\vec {n}}=\{0,1\},~r={\frac {n_{1}}{n_{2}}}=0.9}$

${\displaystyle c=\cos \theta _{1}=0.707107,~{\sqrt {1-r^{2}\left(1-c^{2}\right)}}=\cos \theta _{2}=0.771362}$

${\displaystyle {\vec {v}}_{\mathrm {reflect} }=\{0.707107,0.707107\},~{\vec {v}}_{\mathrm {refract} }=\{0.636396,-0.771362\}}$

Значения косинуса можно сохранить и использовать в Уравнения Френеля для определения интенсивности получаемых лучей.

Полное внутреннее отражение обозначается отрицательным прикорневой в уравнении для ${\displaystyle \cos \theta _{2}}$, что может произойти только при переходе лучей в менее плотную среду (${\displaystyle n_{2}<n_{1}}$).

Полное внутреннее отражение и критический угол

Демонстрация отсутствия рефракции при углах больше критического.

Основная статья: Полное внутреннее отражение

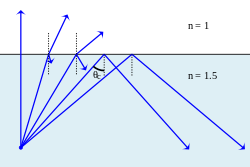
Когда свет проходит от среды с более высоким показателем преломления к среде с более низким показателем преломления, закон Снеллиуса, по-видимому, требует в некоторых случаях (когда угол падения достаточно большой), чтобы синус угла преломления был больше единицы. Это, конечно, невозможно, и свет в таких случаях полностью отражается границей, явление, известное как полное внутреннее отражение. Максимально возможный угол падения, который все еще приводит к преломлению луча, называется углом. критический угол; в этом случае преломленный луч проходит по границе между двумя средами.

Преломление света на границе раздела двух сред.

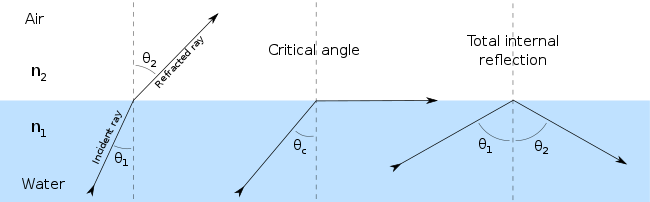
Например, представьте себе луч света, движущийся из воды в воздух под углом падения 50 °. Показатели преломления воды и воздуха равны примерно 1,333 и 1 соответственно, поэтому закон Снеллиуса дает нам соотношение

${\displaystyle \sin \theta _{2}={\frac {n_{1}}{n_{2}}}\sin \theta _{1}={\frac {1.333}{1}}\cdot \sin \left(50^{\circ }\right)=1.333\cdot 0.766=1.021,}$

что невозможно удовлетворить. Критический угол θ_крит - значение θ₁ для которого θ₂ равно 90 °:

${\displaystyle \theta _{\text{crit}}=\arcsin \left({\frac {n_{2}}{n_{1}}}\sin \theta _{2}\right)=\arcsin {\frac {n_{2}}{n_{1}}}=48.6^{\circ }.}$

Дисперсия

Основная статья: Дисперсия (оптика)

Во многих средах распространения волн скорость волны изменяется в зависимости от частоты или длины волны; это верно для распространения света в большинстве прозрачных веществ, кроме вакуума. Эти среды называют дисперсионными. В результате углы, определяемые законом Снеллиуса, также зависят от частоты или длины волны, так что луч со смешанной длиной волны, такой как белый свет, будет распространяться или рассеиваться. Такое рассеяние света в стекле или воде лежит в основе происхождения радуги и другие оптические явления, в котором разные длины волн отображаются разными цветами.

В оптических приборах дисперсия приводит к Хроматическая аберрация; цветозависимое размытие, которое иногда является эффектом ограничения разрешения. Это было особенно актуально в преломляющие телескопы, до изобретения ахроматический линзы объектива.

Потери, поглощающие или проводящие медиа

Смотрите также: Математические описания непрозрачности

В проводящей среде диэлектрическая проницаемость и показатель преломления являются комплексными. Следовательно, таковы угол преломления и волновой вектор. Это означает, что, в то время как поверхности постоянной реальной фазы являются плоскостями, нормали которых составляют угол, равный углу преломления с нормалью границы раздела, поверхности постоянной амплитуды, напротив, являются плоскостями, параллельными самой границе раздела. Поскольку эти две плоскости в общем случае не совпадают друг с другом, волна называется неоднородной.^[18] Преломленная волна экспоненциально затухает, причем показатель степени пропорционален мнимой составляющей показателя преломления.^[19][20]

Смотрите также

• Список показателей преломления
• Показатель преломления в зависимости от длины волны света
• Неувядающая волна
• Отражение (физика) - Изменение направления волнового фронта на границе между двумя различными средами, так что волновой фронт возвращается в среду, из которой он возник.
• Окно Снеллиуса - Подводное явление из-за закона Снеллиуса
• Вариационное исчисление
• Кривая брахистохрона для простого доказательства Якоба Бернулли
• Гамильтонова оптика
• Расчет ослабления радиоволн в атмосфере
• N-щелевое интерферометрическое уравнение

Рекомендации

1. Дэвид Майкл Харланд (2007). "Кассини на Сатурне: результаты Гюйгенса ". стр.1. ISBN  0-387-26129-X
2. "Птолемей (ок. 100-ок. 170)". Мир научной биографии Эрика Вайнштейна.
3. А. И. Сабра (1981), Теории света от Декарта до Ньютона, Издательство Кембриджского университета. (ср. Павлос Михас, Использование истории в развитии идей преломления, линз и радуги, п. 5, Университет Демокрит, Фракия, Греция.)
4. Уильям Уэвелл, История индуктивной науки с древнейших времен до наших дней, Лондон: Джон Х. Паркер, 1837.
5. Рашед, Рошди (1990). «Пионер в анакластике: Ибн Саль о горящих зеркалах и линзах». Исида. 81 (3): 464–491. Дои:10.1086/355456. S2CID  144361526.^{[оспаривается ][требуется разъяснение ]}
6. Kwan, A .; Дадли, Дж .; Ланц, Э. (2002). «Кто на самом деле открыл закон Снеллиуса?». Мир физики. 15 (4): 64. Дои:10.1088/2058-7058/15/4/44.
7. Флориан Каджори, История физики в ее элементарных отраслях: включая эволюцию физических лабораторий (1922)
8. Фердинанд Розенбергер, Geschichte der Physik (1882) Часть. II, стр.114
9. Карл Бенджамин Бойер, Радуга: от мифа к математике (1959)
10. Флориан Каджори, "Кто был первым изобретателем математического анализа" Американский математический ежемесячник (1919) Том 26
11. Геометрия Рене Декарта (Дуврские книги по математике) Рене Декарта, Дэвида Юджина Смита и Марсии Л. Латам (1 июня 1954 г.).
12. Дейкстерхейс, Фокко Ян (2004). Линзы и волны: Христиан Гюйгенс и математическая наука об оптике в семнадцатом веке. Springer. ISBN  1-4020-2697-8.
13. Bloembergen, N .; Першан, П. С. (1962). «Световые волны на границе нелинейных сред» (PDF). Физический обзор. 128 (2): 606. Bibcode:1962ПхРв..128..606Б. Дои:10.1103 / PhysRev.128.606. HDL:1874/7432.
14. Xu, T .; и другие. (2008). «Плазмонный дефлектор». Опт. выражать. 16 (7): 4753–9. Bibcode:2008OExpr..16,4753X. Дои:10.1364 / oe.16.004753. PMID  18542573.
15. Ю, Нанфан; Женевет, Патрис; Кац, Михаил А .; Айета, Франческо; Тетьен, Жан-Филипп; Капассо, Федерико; Габурро, Зенон (октябрь 2011 г.). «Распространение света с разрывами фаз: обобщенные законы отражения и преломления». Наука. 334 (6054): 333–7. Bibcode:2011Наука ... 334..333л. Дои:10.1126 / science.1210713. PMID  21885733. S2CID  10156200.
16. Иоаннопулос, Джон Д.; Джонсон, С. Г.; Winn, JN; Мид, RD (2008). Фотонные кристаллы: формирование потока света (2-е изд.). Принстон, штат Нью-Джерси: Издательство Принстонского университета. ISBN  978-0-691-12456-8.
17. Гласснер, Эндрю С. (1989). Введение в трассировку лучей. Морган Кауфманн. ISBN  0-12-286160-4.
18. Борн и Вольф, раздел 13.2, «Преломление и отражение от металлической поверхности»
19. Гехт, Оптика, сек. 4.8, Оптические свойства металлов.
20. С. Дж. Орфанидис, Электромагнитные волны и антенны, сек. 7.9, Косое падение на потерянной среде, [1]

внешняя ссылка

• Ибн Сахль и закон Снеллиуса
• Открытие закона преломления
• Закон преломления Снеллиуса (волновые фронты) Тодд Роуленд, Вольфрам Демонстрационный проект
• Закон Снеллиуса на стене в центре Лейдена
• Эффект береговой линии
• [2]