Гамма-распределение - Gamma distribution

Гамма

Функция плотности вероятности
Кумулятивная функция распределения
Параметры	k > 0 форма θ > 0 шкала	α > 0 форма β > 0 ставка
Поддерживать	${\displaystyle x\in (0,\infty )}$	${\displaystyle x\in (0,\infty )}$
PDF	${\displaystyle f(x)={\frac {1}{\Gamma (k)\theta ^{k}}}x^{k-1}e^{-{\frac {x}{\theta }}}}$	${\displaystyle f(x)={\frac {\beta ^{\alpha }}{\Gamma (\alpha )}}x^{\alpha -1}e^{-\beta x}}$
CDF	${\displaystyle F(x)={\frac {1}{\Gamma (k)}}\gamma \left(k,{\frac {x}{\theta }}\right)}$	${\displaystyle F(x)={\frac {1}{\Gamma (\alpha )}}\gamma (\alpha ,\beta x)}$
Иметь в виду	${\displaystyle k\theta }$	${\displaystyle {\frac {\alpha }{\beta }}}$
Медиана	Нет простой закрытой формы	Нет простой закрытой формы
Режим	${\displaystyle (k-1)\theta {\text{ for }}k\geq 1}$	${\displaystyle {\frac {\alpha -1}{\beta }}{\text{ for }}\alpha \geq 1}$
Дисперсия	${\displaystyle k\theta ^{2}}$	${\displaystyle {\frac {\alpha }{\beta ^{2}}}}$
Асимметрия	${\displaystyle {\frac {2}{\sqrt {k}}}}$	${\displaystyle {\frac {2}{\sqrt {\alpha }}}}$
Бывший. эксцесс	${\displaystyle {\frac {6}{k}}}$	${\displaystyle {\frac {6}{\alpha }}}$
Энтропия	${\displaystyle {\begin{aligned}k&+\ln \theta +\ln \Gamma (k)\\&+(1-k)\psi (k)\end{aligned}}}$	${\displaystyle {\begin{aligned}\alpha &-\ln \beta +\ln \Gamma (\alpha )\\&+(1-\alpha )\psi (\alpha )\end{aligned}}}$
MGF	${\displaystyle (1-\theta t)^{-k}{\text{ for }}t<{\frac {1}{\theta }}}$	${\displaystyle \left(1-{\frac {t}{\beta }}\right)^{-\alpha }{\text{ for }}t<\beta }$
CF	${\displaystyle (1-\theta it)^{-k}}$	${\displaystyle \left(1-{\frac {it}{\beta }}\right)^{-\alpha }}$
Метод моментов	${\displaystyle k={\frac {E[X]^{2}}{V[X]}}\quad \quad }$ ${\displaystyle \theta ={\frac {V[X]}{E[X]}}\quad \quad }$	${\displaystyle \alpha ={\frac {E[X]^{2}}{V[X]}}}$ ${\displaystyle \beta ={\frac {E[X]}{V[X]}}}$

В теория вероятности и статистика, то гамма-распределение это двух-параметр семья непрерывных распределения вероятностей. В экспоненциальное распределение, Распределение Erlang, и распределение хи-квадрат являются частными случаями гамма-распределения. Есть три разных параметризации в общем использовании:

1. С параметр формы k и параметр масштаба θ.
2. С параметром формы α = k и параметр обратного масштаба β = 1/θ, называется параметр скорости.
3. С параметром формы k и средний параметр μ = kθ = α/β.

В каждой из этих трех форм оба параметра являются положительными действительными числами.

Гамма-распределение - это распределение вероятностей максимальной энтропии (как относительно единой базовой меры, так и относительно 1 /Икс базовая мера) для случайной величины Икс для которого E[Икс] = kθ = α/β фиксировано и больше нуля, и E[ln (Икс)] = ψ(k) + ln (θ) = ψ(α) - ln (β) фиксированный (ψ это функция дигаммы ).^[1]

Определения

Параметризация с k и θ кажется более распространенным в эконометрика и некоторых других прикладных областях, где, например, гамма-распределение часто используется для моделирования времени ожидания. Например, в жизненное испытание, время ожидания смерти - это случайная переменная который часто моделируется с помощью гамма-распределения. Увидеть Хогга и Крейга^[2] для явной мотивации.

Параметризация с α и β чаще встречается в Байесовская статистика, где гамма-распределение используется как сопряженный предшествующий распределения для различных типов параметров обратной шкалы (ставки), таких как λ из экспоненциальное распределение или распределение Пуассона^[3] - или, если на то пошло, β самого гамма-распределения. Тесно связанные обратное гамма-распределение используется в качестве сопряженного априорного значения для параметров масштаба, таких как отклонение из нормальное распределение.

Если k положительный целое число, то распределение представляет собой Распределение Erlang; т.е. сумма k независимый экспоненциально распределенный случайные переменные, каждый из которых имеет среднее значение θ.

Характеристика с помощью формы α и оценить β

Гамма-распределение может быть параметризовано с помощью параметр формы α = k и параметр обратного масштаба β = 1/θ, называется параметр скорости. Случайная величина Икс гамма-распределение с формой α и оценить β обозначается

${\displaystyle X\sim \Gamma (\alpha ,\beta )\equiv \operatorname {Gamma} (\alpha ,\beta )}$

Соответствующая функция плотности вероятности в параметризации скорости формы равна

${\displaystyle {\begin{aligned}f(x;\alpha ,\beta )&={\frac {\beta ^{\alpha }x^{\alpha -1}e^{-\beta x}}{\Gamma (\alpha )}}\quad {\text{ for }}x>0\quad \alpha ,\beta >0,\\[6pt]\end{aligned}}}$

куда ${\displaystyle \Gamma (\alpha )}$ это гамма-функция. Для всех положительных целых чисел ${\displaystyle \Gamma (\alpha )=(\alpha -1)!}$.

В кумулятивная функция распределения - регуляризованная гамма-функция:

${\displaystyle F(x;\alpha ,\beta )=\int _{0}^{x}f(u;\alpha ,\beta )\,du={\frac {\gamma (\alpha ,\beta x)}{\Gamma (\alpha )}},}$

куда ${\displaystyle \gamma (\alpha ,\beta x)}$ это нижний неполная гамма-функция.

Если α положительный целое число (т.е. распределение является Распределение Erlang ) кумулятивная функция распределения имеет следующее разложение в ряд:^[4]

${\displaystyle F(x;\alpha ,\beta )=1-\sum _{i=0}^{\alpha -1}{\frac {(\beta x)^{i}}{i!}}e^{-\beta x}=e^{-\beta x}\sum _{i=\alpha }^{\infty }{\frac {(\beta x)^{i}}{i!}}.}$

Характеристика с помощью формы k и масштабировать θ

Случайная величина Икс гамма-распределение с формой k и масштабировать θ обозначается

${\displaystyle X\sim \Gamma (k,\theta )\equiv \operatorname {Gamma} (k,\theta )}$

Иллюстрация гамма-PDF для значений параметров свыше k и Икс с θ установлен на 1, 2, 3, 4, 5 и 6. Можно увидеть каждый θ слой сам по себе здесь [2] а такжеk [3] иИкс. [4].

В функция плотности вероятности с использованием параметризации в масштабе формы

${\displaystyle f(x;k,\theta )={\frac {x^{k-1}e^{-{\frac {x}{\theta }}}}{\theta ^{k}\Gamma (k)}}\quad {\text{ for }}x>0{\text{ and }}k,\theta >0.}$

Здесь Γ (k) это гамма-функция оценивается в k.

В кумулятивная функция распределения - регуляризованная гамма-функция:

${\displaystyle F(x;k,\theta )=\int _{0}^{x}f(u;k,\theta )\,du={\frac {\gamma \left(k,{\frac {x}{\theta }}\right)}{\Gamma (k)}},}$

куда ${\displaystyle \gamma \left(k,{\frac {x}{\theta }}\right)}$ это нижний неполная гамма-функция.

Также это можно выразить следующим образом, если k положительный целое число (т.е. распределение является Распределение Erlang ):^[4]

${\displaystyle F(x;k,\theta )=1-\sum _{i=0}^{k-1}{\frac {1}{i!}}\left({\frac {x}{\theta }}\right)^{i}e^{-x/\theta }=e^{-x/\theta }\sum _{i=k}^{\infty }{\frac {1}{i!}}\left({\frac {x}{\theta }}\right)^{i}.}$

Обе параметризации являются общими, поскольку любая из них может быть более удобной в зависимости от ситуации.

Характеристики

Асимметрия

Асимметрия гамма-распределения зависит только от его параметра формы, k, и он равен ${\displaystyle 2/{\sqrt {k}}.}$

Расчет медианы

В отличие от режима и среднего, которые имеют легко вычисляемые формулы на основе параметров, медиана не имеет уравнения в замкнутой форме. Медиана этого распределения определяется как значение ${\displaystyle \nu }$ такой, что

${\displaystyle {\frac {1}{\Gamma (k)\theta ^{k}}}\int _{0}^{\nu }x^{k-1}e^{-x/\theta }dx={\frac {1}{2}}.}$

Строгий подход к проблеме определения асимптотического разложения и оценок медианы гамма-распределения был впервые проведен Ченом и Рубином, которые доказали, что (для ${\displaystyle \theta =1}$)

${\displaystyle \mu -{\frac {1}{3}}<\nu <\mu ,}$

куда ${\displaystyle \mu =k}$ это среднее и ${\displaystyle \nu }$ это медиана ${\displaystyle {\text{Gamma}}(k,1)}$ распространение.^[5]

К. П. Чой нашел первые пять членов в асимптотическом разложении медианы, сравнив медиану с оценкой Рамануджана. ${\displaystyle \theta }$ функция.^[6] Берг и Педерсен нашли больше терминов:^[7]

${\displaystyle \nu =k-{\frac {1}{3}}+{\frac {8}{405k}}+{\frac {184}{25515k^{2}}}+{\frac {2248}{3444525k^{3}}}-{\frac {19006408}{15345358875k^{4}}}-O\left({\frac {1}{k^{5}}}\right)+\cdots }$

Они также доказали многие свойства медианы, показали, что ${\displaystyle \nu }$ является выпуклой функцией от ${\displaystyle k}$,^[8] и показал, что асимптотика вблизи ${\displaystyle \mu =0}$ является ${\displaystyle \nu =e^{-\gamma }2^{-1/k}}$.^[7]

Суммирование

Если Икс_я имеет гамму (k_я, θ) раздача для я = 1, 2, ..., N (т.е. все распределения имеют одинаковый масштабный параметр θ), тогда

${\displaystyle \sum _{i=1}^{N}X_{i}\sim \mathrm {Gamma} \left(\sum _{i=1}^{N}k_{i},\theta \right)}$

при условии, что все Икс_я находятся независимый.

Для случаев, когда Икс_я находятся независимый но имеют разные параметры масштаба см. Матхай ^[9] или Moschopoulos.^[10]

Гамма-распределение показывает бесконечная делимость.

Масштабирование

Если

${\displaystyle X\sim \mathrm {Gamma} (k,\theta ),}$

тогда для любого c > 0,

${\displaystyle cX\sim \mathrm {Gamma} (k,c\,\theta ),}$ по моментным производящим функциям,

или эквивалентно

${\displaystyle cX\sim \mathrm {Gamma} \left(\alpha ,{\frac {\beta }{c}}\right),}$

Действительно, мы знаем, что если Икс является экспоненциальная с.в. со скоростью λ тогда cX - экспоненциальная с.в. со скоростью λ/c; то же самое верно и с вариациями гаммы (и это можно проверить с помощью момент-производящая функция см., например,эти заметки, 10.4- (ii)): умножение на положительную константу c делит ставку (или, что то же самое, умножает шкалу).

Экспоненциальная семья

Гамма-распределение - двухпараметрическое экспоненциальная семья с естественные параметры k - 1 и −1 /θ (эквивалентно, α - 1 и -β), и естественная статистика Икс и ln (Икс).

Если параметр формы k фиксируется, результирующее однопараметрическое семейство распределений представляет собой естественная экспоненциальная семья.

Логарифмическое ожидание и дисперсия

Можно показать, что

${\displaystyle \operatorname {E} [\ln(X)]=\psi (\alpha )-\ln(\beta )}$

или эквивалентно,

${\displaystyle \operatorname {E} [\ln(X)]=\psi (k)+\ln(\theta )}$

куда ψ это функция дигаммы. Точно так же

${\displaystyle \operatorname {var} [\ln(X)]=\psi ^{(1)}(\alpha )=\psi ^{(1)}(k)}$

куда ${\displaystyle \psi ^{(1)}}$ это функция тригаммы.

Это можно вывести с помощью экспоненциальная семья формула для моментная производящая функция достаточной статистики, поскольку одной из достаточных статистик гамма-распределения является ln (Икс).

Информационная энтропия

В информационная энтропия является

${\displaystyle {\begin{aligned}\operatorname {H} (X)&=\operatorname {E} [-\ln(p(X))]\\&=\operatorname {E} [-\alpha \ln(\beta )+\ln(\Gamma (\alpha ))-(\alpha -1)\ln(X)+\beta X]\\&=\alpha -\ln(\beta )+\ln(\Gamma (\alpha ))+(1-\alpha )\psi (\alpha ).\end{aligned}}}$

в k, θ параметризация, информационная энтропия дан кем-то

${\displaystyle \operatorname {H} (X)=k+\ln(\theta )+\ln(\Gamma (k))+(1-k)\psi (k).}$

Дивергенция Кульбака – Лейблера

Иллюстрация дивергенции Кульбака – Лейблера (КЛ) для двух гамма-PDF. Здесь β = β₀ + 1, которые установлены на 1, 2, 3, 4, 5 и 6. Типичная асимметрия для расхождения KL хорошо видна.

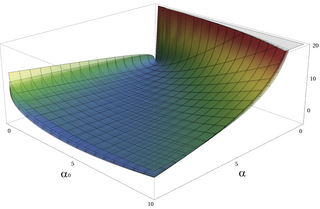
В Дивергенция Кульбака – Лейблера (KL-дивергенция), гамма (α_п, β_п) ("истинное" распределение) от Gamma (α_q, β_q) ("аппроксимирующее" распределение) определяется выражением^[11]

${\displaystyle {\begin{aligned}D_{\mathrm {KL} }(\alpha _{p},\beta _{p};\alpha _{q},\beta _{q})={}&(\alpha _{p}-\alpha _{q})\psi (\alpha _{p})-\log \Gamma (\alpha _{p})+\log \Gamma (\alpha _{q})\\&{}+\alpha _{q}(\log \beta _{p}-\log \beta _{q})+\alpha _{p}{\frac {\beta _{q}-\beta _{p}}{\beta _{p}}}.\end{aligned}}}$

Написано с использованием k, θ параметризация, KL-дивергенция гамма (k_п, θ_п) из гаммы (k_q, θ_q) дан кем-то

${\displaystyle {\begin{aligned}D_{\mathrm {KL} }(k_{p},\theta _{p};k_{q},\theta _{q})={}&(k_{p}-k_{q})\psi (k_{p})-\log \Gamma (k_{p})+\log \Gamma (k_{q})\\&{}+k_{q}(\log \theta _{q}-\log \theta _{p})+k_{p}{\frac {\theta _{p}-\theta _{q}}{\theta _{q}}}.\end{aligned}}}$

Преобразование Лапласа

В Преобразование Лапласа гамма PDF

${\displaystyle F(s)=(1+\theta s)^{-k}={\frac {\beta ^{\alpha }}{(s+\beta )^{\alpha }}}.}$

Связанные дистрибутивы

Общее

• Позволять ${\displaystyle X_{1},X_{2}\ldots X_{n}}$ быть ${\displaystyle n}$ независимых и одинаково распределенных случайных величин, следующих за экспоненциальное распределение с параметром скорости λ, то ${\displaystyle \sum _{i}X_{i}}$ ~ Gamma (n, 1 / λ), где n - параметр формы, а 1 / λ - масштаб.
• Если Икс ~ Gamma (1, 1 / λ) (параметризация формы и масштаба), тогда Икс имеет экспоненциальное распределение с параметром скорости λ.
• Если Икс ~ Gamma (ν / 2, 2) (параметризация формы и масштаба), тогда Икс идентичен χ²(ν), распределение хи-квадрат с ν степени свободы. Наоборот, если Q ~ χ²(ν) и c положительная константа, то cQ ~ Гамма (ν/2, 2c).
• Если k является целое число, гамма-распределение представляет собой Распределение Erlang и - распределение вероятностей времени ожидания до kй "приход" в одномерном Пуассоновский процесс с интенсивностью 1 /θ. Если

${\displaystyle X\sim \Gamma (k\in \mathbf {Z} ,\theta ),\qquad Y\sim \mathrm {Pois} \left({\frac {x}{\theta }}\right),}$

тогда

${\displaystyle P(X>x)=P(Y<k).}$

• Если Икс имеет Распределение Максвелла – Больцмана с параметром а, тогда

${\displaystyle X^{2}\sim \Gamma \left({\frac {3}{2}},2a^{2}\right)}$.

• Если Икс ~ Гамма (k, θ), тогда ${\displaystyle \log {X}}$ следует экспоненциально-гамма-распределению (сокращенно exp-gammma).^[12] Иногда его называют логарифмически-гамма-распределением.^[13] Формулы для его среднего и дисперсии находятся в разделе # Логарифмическое ожидание и дисперсия.
• Если Икс ~ Гамма (k, θ), тогда ${\displaystyle {\sqrt {X}}}$ следует за обобщенное гамма-распределение с параметрами п = 2, d = 2k, и ${\displaystyle a={\sqrt {\theta }}}$^{[нужна цитата ]}.
• В более общем смысле, если Икс ~ Гамма (k,θ), тогда ${\displaystyle X^{q}}$ за ${\displaystyle q>0}$ следует за обобщенное гамма-распределение с параметрами п = 1/q, d = k/q, и ${\displaystyle a=\theta ^{q}}$.
• Если Икс ~ Гамма (k, θ), то 1 /Икс ~ Инв-Гамма (k, θ⁻¹) (увидеть Обратное гамма-распределение для вывода).
• Параметризация 1: Если ${\displaystyle X_{k}\sim \Gamma (\alpha _{k},\theta _{k})\,}$ независимы, то ${\displaystyle {\frac {\alpha _{2}\theta _{2}X_{1}}{\alpha _{1}\theta _{1}X_{2}}}\sim \mathrm {F} (2\alpha _{1},2\alpha _{2})}$, или эквивалентно, ${\displaystyle {\frac {X_{1}}{X_{2}}}\sim \beta '\left(\alpha _{1},\alpha _{2},1,{\frac {\theta _{1}}{\theta _{2}}}\right)}$
• Параметризация 2: Если ${\displaystyle X_{k}\sim \Gamma (\alpha _{k},\beta _{k})\,}$ независимы, то ${\displaystyle {\frac {\alpha _{2}\beta _{1}X_{1}}{\alpha _{1}\beta _{2}X_{2}}}\sim \mathrm {F} (2\alpha _{1},2\alpha _{2})}$, или эквивалентно, ${\displaystyle {\frac {X_{1}}{X_{2}}}\sim \beta '\left(\alpha _{1},\alpha _{2},1,{\frac {\beta _{2}}{\beta _{1}}}\right)}$
• Если Икс ~ Гамма (α, θ) и Y ~ Гамма (β, θ) распределены независимо, то Икс/(Икс + Y) имеет бета-распространение с параметрами α и β, и Икс/(Икс + Y) не зависит от Икс + Y, то есть Гамма (α + β, θ) -распределены.
• Если Икс_я ~ Гамма (α_я, 1) распределены независимо, то вектор (Икс₁/S, ..., Икс_п/S), куда S = Икс₁ + ... + Икс_п, следует за Распределение Дирихле с параметрами α₁, ..., α_п.
• Для больших k гамма-распределение сходится к нормальное распределение со средним μ = kθ и дисперсия σ² = kθ².
• Гамма-распределение - это сопряженный предшествующий для точности нормальное распределение с известными иметь в виду.
• В Распределение Уишарта является многомерным обобщением гамма-распределения (выборки представляют собой положительно определенные матрицы, а не положительные действительные числа).
• Гамма-распределение - это частный случай обобщенное гамма-распределение, то обобщенное целочисленное гамма-распределение, а обобщенное обратное гауссово распределение.
• Среди дискретных распределений отрицательное биномиальное распределение иногда рассматривается как дискретный аналог гамма-распределения.
• Распределения твиди - гамма-распределение принадлежит к семейству Tweedie модели экспоненциальной дисперсии.

Составная гамма

Если параметр формы гамма-распределения известен, но параметр обратного масштаба неизвестен, то гамма-распределение для обратного масштаба образует сопряженный априор. В составное распределение, который является результатом интегрирования обратной шкалы, имеет решение в замкнутой форме, известное как составное гамма-распределение.^[14]

Если вместо этого параметр формы известен, но среднее значение неизвестно, а априор среднего значения задается другим гамма-распределением, то это приводит к K-распределение.

Статистические выводы

Оценка параметров

Оценка максимального правдоподобия

Функция правдоподобия для N iid наблюдения (Икс₁, ..., Икс_N) является

${\displaystyle L(k,\theta )=\prod _{i=1}^{N}f(x_{i};k,\theta )}$

из которого мы вычисляем функцию логарифма правдоподобия

${\displaystyle \ell (k,\theta )=(k-1)\sum _{i=1}^{N}\ln(x_{i})-\sum _{i=1}^{N}{\frac {x_{i}}{\theta }}-Nk\ln(\theta )-N\ln(\Gamma (k))}$

Нахождение максимума по θ взяв производную и установив ее равной нулю, получаем максимальная вероятность оценщик θ параметр:

${\displaystyle {\hat {\theta }}={\frac {1}{kN}}\sum _{i=1}^{N}x_{i}}$

Подставляя это в функцию логарифма правдоподобия, получаем

${\displaystyle \ell =(k-1)\sum _{i=1}^{N}\ln(x_{i})-Nk-Nk\ln \left({\frac {\sum x_{i}}{kN}}\right)-N\ln(\Gamma (k))}$

Нахождение максимума по k взяв производную и установив ее равной нулю, получаем

${\displaystyle \ln(k)-\psi (k)=\ln \left({\frac {1}{N}}\sum _{i=1}^{N}x_{i}\right)-{\frac {1}{N}}\sum _{i=1}^{N}\ln(x_{i})}$

куда ψ это функция дигаммы. Нет закрытого решения для k. Функция имеет очень хорошее числовое поведение, поэтому, если требуется численное решение, его можно найти, например, с помощью Метод Ньютона. Начальное значение k можно найти либо с помощью метод моментов, или используя приближение

${\displaystyle \ln(k)-\psi (k)\approx {\frac {1}{2k}}\left(1+{\frac {1}{6k+1}}\right)}$

Если мы позволим

${\displaystyle s=\ln \left({\frac {1}{N}}\sum _{i=1}^{N}x_{i}\right)-{\frac {1}{N}}\sum _{i=1}^{N}\ln(x_{i})}$

тогда k примерно

${\displaystyle k\approx {\frac {3-s+{\sqrt {(s-3)^{2}+24s}}}{12s}}}$

что находится в пределах 1,5% от правильного значения.^[15] Явная форма обновления этого начального предположения по Ньютону – Рафсону:^[16]

${\displaystyle k\leftarrow k-{\frac {\ln(k)-\psi (k)-s}{{\frac {1}{k}}-\psi ^{\prime }(k)}}.}$

Оценщики в закрытой форме

Последовательные оценки в закрытой форме k и θ существуют, которые получены из вероятности обобщенное гамма-распределение.^[17]

Оценка формы k является

${\displaystyle {\hat {k}}={\frac {N\sum _{i=1}^{N}x_{i}}{N\sum _{i=1}^{N}x_{i}\ln(x_{i})-\sum _{i=1}^{N}\ln(x_{i})\sum _{i=1}^{N}x_{i}}}}$

и оценка масштаба θ является

${\displaystyle {\hat {\theta }}={\frac {1}{N^{2}}}\left(N\sum _{i=1}^{N}x_{i}\ln(x_{i})-\sum _{i=1}^{N}\ln(x_{i})\sum _{i=1}^{N}x_{i}\right)}$

Если используется параметризация скорости, оценка ${\displaystyle {\hat {\beta }}={\frac {1}{\hat {\theta }}}}$.

Эти оценщики не являются строго оценщиками максимального правдоподобия, а вместо этого называются оценщиками логарифмического момента смешанного типа. Однако они имеют такую ​​же эффективность, что и оценки максимального правдоподобия.

Хотя эти оценки согласованы, они имеют небольшую погрешность. Вариант оценки для шкалы с поправкой на смещение θ является

${\displaystyle {\tilde {\theta }}={\frac {N}{N-1}}{\hat {\theta }}}$

Корректировка смещения для параметра формы k дается как^[18]

${\displaystyle {\tilde {k}}={\hat {k}}-{\frac {1}{N}}\left(3{\hat {k}}-{\frac {2}{3}}\left({\frac {\hat {k}}{1+{\hat {k}}}}\right)-{\frac {4}{5}}{\frac {\hat {k}}{(1+{\hat {k}})^{2}}}\right)}$

Минимальная байесовская среднеквадратическая ошибка

С известными k и неизвестно θ, апостериорная функция плотности для тета (с использованием стандартного масштабно-инвариантного прежний за θ) является

${\displaystyle P(\theta \mid k,x_{1},\dots ,x_{N})\propto {\frac {1}{\theta }}\prod _{i=1}^{N}f(x_{i};k,\theta )}$

Обозначение

${\displaystyle y\equiv \sum _{i=1}^{N}x_{i},\qquad P(\theta \mid k,x_{1},\dots ,x_{N})=C(x_{i})\theta ^{-Nk-1}e^{-y/\theta }}$

Интеграция в отношении θ можно провести заменой переменных, обнаружив, что 1 /θ гамма-распределение с параметрами α = Nk, β = у.

${\displaystyle \int _{0}^{\infty }\theta ^{-Nk-1+m}e^{-y/\theta }\,d\theta =\int _{0}^{\infty }x^{Nk-1-m}e^{-xy}\,dx=y^{-(Nk-m)}\Gamma (Nk-m)\!}$

Моменты можно вычислить, взяв отношение (м к м = 0)

${\displaystyle \operatorname {E} [x^{m}]={\frac {\Gamma (Nk-m)}{\Gamma (Nk)}}y^{m}}$

который показывает, что оценка среднего ± стандартное отклонение апостериорного распределения для θ является

${\displaystyle {\frac {y}{Nk-1}}\pm {\sqrt {\frac {y^{2}}{(Nk-1)^{2}(Nk-2)}}}.}$

Байесовский вывод

Конъюгировать приор

В Байесовский вывод, то гамма-распределение это сопряженный предшествующий ко многим вероятностным распределениям: Пуассон, экспоненциальный, нормальный (с известным средним), Парето, гамма известной формы σ, обратная гамма с известным параметром формы, и Гомпертц с известным масштабным параметром.

Гамма-распределение сопряженный предшествующий является:^[19]

${\displaystyle p(k,\theta \mid p,q,r,s)={\frac {1}{Z}}{\frac {p^{k-1}e^{-\theta ^{-1}q}}{\Gamma (k)^{r}\theta ^{ks}}},}$

куда Z - нормализующая константа, не имеющая решения в замкнутой форме. Апостериорное распределение можно найти, обновив параметры следующим образом:

${\displaystyle {\begin{aligned}p'&=p\prod \nolimits _{i}x_{i},\\q'&=q+\sum \nolimits _{i}x_{i},\\r'&=r+n,\\s'&=s+n,\end{aligned}}}$

куда п - количество наблюдений, а Икс_я это я-е наблюдение.

Возникновение и приложения

Гамма-распределение использовалось для моделирования размера страховые выплаты^[20] и осадки.^[21] Это означает, что совокупные страховые выплаты и количество осадков, накопленных в водохранилище, моделируются с помощью гамма-процесс - очень похоже на экспоненциальное распределение генерирует Пуассоновский процесс.

Гамма-распределение также используется для моделирования ошибок в многоуровневых Регрессия Пуассона модели, потому что смесь из Распределения Пуассона с гамма-распределением ставок имеет известное распределение в закрытой форме, называемое отрицательный бином.

В беспроводной связи гамма-распределение используется для моделирования многолучевое замирание мощности сигнала;^{[нужна цитата ]} смотрите также Распределение Рэлея и Райское распределение.

В онкология, возрастное распределение рак заболеваемость часто следует за гамма-распределением, тогда как параметры формы и масштаба предсказывают, соответственно, количество события водителя и временной интервал между ними.^[22]

В нейробиология, гамма-распределение часто используется для описания распределения межспайковые интервалы.^[23][24]

В бактериальный экспрессия гена, то номер копии из конститутивно выраженный белок часто следует гамма-распределению, где масштаб и параметр формы представляют собой, соответственно, среднее количество всплесков на клеточный цикл и среднее количество белковые молекулы продуцируется одной мРНК в течение своей жизни.^[25]

В геномика, гамма-распределение применялось в пик вызова шаг (т.е. распознавание сигнала) в ЧИП-чип^[26] и ChIP-seq^[27] анализ данных.

Гамма-распределение широко используется как сопряженный предшествующий в байесовской статистике. Это сопряженная априорная величина для точности (то есть обратная дисперсии) нормальное распределение. Это также сопряженный априор для экспоненциальное распределение.

Генерация случайных величин с гамма-распределением

Учитывая указанное выше свойство масштабирования, достаточно сгенерировать гамма-переменные с θ = 1, так как позже мы можем преобразовать в любое значение β с простым делением.

Предположим, мы хотим сгенерировать случайные величины из Gamma (п + δ, 1), где n - целое неотрицательное число и 0 < δ <1. Используя тот факт, что распределение Gamma (1, 1) совпадает с распределением Exp (1), и отмечая метод генерация экспоненциальных переменных, заключаем, что если U является равномерно распределены на (0, 1], то −ln (U) распределен Gamma (1, 1) (т.е. выборка с обратным преобразованием ). Теперь, используя "α-добавление свойства гамма-распределения, расширяем этот результат:

${\displaystyle -\sum _{k=1}^{n}\ln U_{k}\sim \Gamma (n,1)}$

куда U_k все равномерно распределены на (0, 1] и независимый. Теперь осталось только сгенерировать переменную, распределенную как Gamma (δ, 1) для 0 < δ <1 и примените "α-добавление еще раз. Это самая сложная часть.

Случайная генерация гамма-переменных подробно обсуждается Devroye,^{[28]:401–428} отмечая, что ни один из них не является равномерно быстрым для всех параметров формы. При малых значениях параметра формы алгоритмы часто не работают.^[28]:406 Для произвольных значений параметра формы можно применить метод Аренса и Дитера.^[29] модифицированный метод приемки-брака Алгоритм GD (форма k ≥ 1) или метод преобразования^[30] когда 0 < k <1. См. Также Cheng and Feast Algorithm GKM 3.^[31] или метод сжатия Марсальи.^[32]

Ниже приводится версия Аренса-Дитера. метод приема – отказа:^[29]

1. Генерировать U, V и W так как iid uniform (0, 1] изменяется.
2. Если ${\displaystyle U\leq {\frac {e}{e+\delta }}}$ тогда ${\displaystyle \xi =V^{1/\delta }}$ и ${\displaystyle \eta =W\xi ^{\delta -1}}$. Иначе, ${\displaystyle \xi =1-\ln V}$ и ${\displaystyle \eta =We^{-\xi }}$.
3. Если ${\displaystyle \eta >\xi ^{\delta -1}e^{-\xi }}$ затем переходите к шагу 1.
4. ξ распределяется как Γ (δ, 1).

Краткое изложение этого

${\displaystyle \theta \left(\xi -\sum _{i=1}^{\lfloor k\rfloor }\ln(U_{i})\right)\sim \Gamma (k,\theta )}$

куда ${\displaystyle \scriptstyle \lfloor k\rfloor }$ это целая часть k, ξ генерируется с помощью алгоритма выше с δ = {k} (дробная часть k) и U_k все независимы.

Хотя описанный выше подход технически верен, Деврой отмечает, что он линейен в отношении значения k да и вообще не удачный выбор. Вместо этого он рекомендует использовать методы на основе отклонения или таблицы, в зависимости от контекста.^{[28]:401–428}

Например, простой метод отклонения преобразования Марсальи, основанный на одной нормальной переменной Икс и один вариант униформы U:^[33]

1. Набор ${\displaystyle d=a-{\frac {1}{3}}}$ и ${\displaystyle c={\frac {1}{\sqrt {9d}}}}$.
2. Набор ${\displaystyle v=(1+cX)^{3}}$.
3. Если ${\displaystyle v>0}$ и ${\displaystyle \ln U<{\frac {X^{2}}{2}}+d-dv+d\ln v}$ возвращаться ${\displaystyle dv}$, иначе вернитесь к шагу 2.

С участием ${\displaystyle 1\leq a=\alpha =k}$ генерирует случайное число с гамма-распределением во времени, которое приблизительно постоянно с k. Скорость приема зависит от k, со степенью приемки 0,95, 0,98 и 0,99 для k = 1, 2 и 4. Для k <1, можно использовать ${\displaystyle \gamma _{\alpha }=\gamma _{1+\alpha }U^{1/\alpha }}$ поднять k для использования с этим методом.

Примечания

1. Park, Sung Y .; Бера, Анил К. (2009). «Модель условной гетероскедастичности авторегрессии с максимальной энтропией» (PDF). Журнал эконометрики. 150 (2): 219–230. CiteSeerX  10.1.1.511.9750. Дои:10.1016 / j.jeconom.2008.12.014. Архивировано из оригинал (PDF) на 2016-03-07. Получено 2011-06-02.
2. Хогг, Р.В.; Крейг, А. Т. (1978). Введение в математическую статистику (4-е изд.). Нью-Йорк: Макмиллан. С. Замечание 3.3.1. ISBN  0023557109.
3. Масштабируемая рекомендация с факторизацией Пуассона, Прем Гопалан, Джейк М. Хофман, Дэвид Блей, arXiv.org 2014
4. Папулис, Пиллаи, Вероятность, случайные величины и случайные процессы, Четвертый выпуск
5. Джисен Чен, Герман Рубин, Границы разницы между медианным и средним гамма- и пуассоновым распределениями, Statistics & Probability Letters, том 4, выпуск 6, октябрь 1986 г., страницы 281–283, ISSN  0167-7152, [1].
6. Цой, К. П. «О медианах гамма-распределений и уравнении Рамануджана», Труды Американского математического общества, Vol. 121, № 1 (май 1994 г.), стр. 245–251.
7. Берг, Кристиан и Педерсен, Хенрик Л. (март 2006 г.). «Гипотеза Чена – Рубина в непрерывной ситуации» (PDF). Методы и приложения анализа. 13 (1): 63–88. Дои:10.4310 / MAA.2006.v13.n1.a4. S2CID  6704865. Получено 1 апреля 2020.
8. Берг, Кристиан и Педерсен, Хенрик Л. «Выпуклость медианы в гамма-распределении».
9. Матхай, А. М. (1982). «Вместимость плотины с вводами гамма-типа». Летопись Института статистической математики. 34 (3): 591–597. Дои:10.1007 / BF02481056. ISSN  0020-3157. S2CID  122537756.
10. Moschopoulos, П. Г. (1985). «Распределение суммы независимых гамма-случайных величин». Летопись Института статистической математики. 37 (3): 541–544. Дои:10.1007 / BF02481123. S2CID  120066454.
11. У. Д. Пенни, [www.fil.ion.ucl.ac.uk/~wpenny/publications/densities.ps KL-расхождения плотностей нормальной, гамма-плотности, плотности Дирихле и Вишарта]^{[требуется полная цитата ]}
12. https://reference.wolfram.com/language/ref/ExpGammaDistribution.html
13. https://docs.scipy.org/doc/scipy/reference/generated/scipy.stats.loggamma.html#scipy.stats.loggamma
14. Дубей, Сатья Д. (декабрь 1970 г.). «Составное гамма-, бета- и F-распределения». Метрика. 16: 27–31. Дои:10.1007 / BF02613934. S2CID  123366328.
15. Минка, Томас П. (2002). «Оценка гамма-распределения» (PDF).
16. Choi, S.C .; Wette, R. (1969). «Максимально правдоподобная оценка параметров гамма-распределения и их смещения». Технометрика. 11 (4): 683–690. Дои:10.1080/00401706.1969.10490731.
17. Чжи-Шэн Е и Нань Чен (2017) Оценки в закрытой форме для гамма-распределения, полученные из уравнений правдоподобия Американский статистик, 71: 2, 177-181
18. Франсиско Лузада, Педро Л. Рамос, Эдуардо Рамос. (2019) Примечание о смещении оценок в закрытой форме для гамма-распределения, полученных из уравнений правдоподобия. Американский статистик 73: 2, страницы 195–199.
19. Финк, Д. 1995 Сборник сопряженных приоров. Отчет о выполнении: Расширение и совершенствование методов для постановки целей по качеству данных. (Контракт Министерства энергетики США 95‑831).
20. п. 43, Филип Дж. Боланд, Статистические и вероятностные методы в актуарной науке, Chapman & Hall CRC 2007
21. Аксой, Х. (2000) «Использование гамма-распределения в гидрологическом анализе», Терк Дж. Энгин Энвайрон Сайнс, 24, 419 – 428.
22. Беликов, Алексей В. (22 сентября 2017 г.). «Количество ключевых канцерогенных событий можно предсказать по заболеваемости раком». Научные отчеты. 7 (1): 12170. Дои:10.1038 / s41598-017-12448-7. ЧВК  5610194. PMID  28939880.
23. Дж. Г. Робсон и Дж. Б. Трой, «Природа поддерживаемого разряда Q, X и Y ганглиозных клеток сетчатки кошки», J. Opt. Soc. Являюсь. А 4, 2301–2307 (1987)
24. M.C.M. Райт, И.М. Винтер, Дж. Дж. Форстер, С. Блик «Реакция на тоновые импульсы с наилучшей частотой в вентральном ядре улитки определяется упорядоченной статистикой межспайковых интервалов», Hearing Research 317 (2014)
25. Н. Фридман, Л. Цай и X. С. Се (2006) "Связь стохастической динамики с распределением населения: аналитическая основа экспрессии генов", Phys. Rev. Lett. 97, 168302.
26. DJ Reiss, MT Facciotti и NS Baliga (2008) «Модельная деконволюция связывания ДНК в масштабе всего генома», Биоинформатика, 24, 396–403
27. М.А. Мендоза-Парра, М. Новицка, В. Ван Гул, Г. Гронемейер (2013) «Характеристика паттернов связывания ChIP-seq с помощью деконволюции формы пика на основе модели», BMC Genomics, 14:834
28. Деврой, Люк (1986). Генерация неоднородной случайной величины. Нью-Йорк: Springer-Verlag. ISBN  978-0-387-96305-1. См. Главу 9, раздел 3.
29. Ahrens, J. H .; Дитер, У (январь 1982 г.). «Генерирование гаммы изменяется с помощью модифицированной техники отклонения». Коммуникации ACM. 25 (1): 47–54. Дои:10.1145/358315.358390. S2CID  15128188.. См. Алгоритм GD, стр. 53.
30. Ahrens, J. H .; Дитер, У. (1974). «Компьютерные методы выборки из гамма-, бета-, пуассоновского и биномиального распределений». Вычисление. 12 (3): 223–246. CiteSeerX  10.1.1.93.3828. Дои:10.1007 / BF02293108. S2CID  37484126.
31. Cheng, R.C.H., и Feast, G.M. Некоторые простые генераторы гамма-изменения. Appl. Стат. 28 (1979), 290–295.
32. Марсалья, Г. Метод сжатия для генерации гамма-вариаций. Comput, Math. Appl. 3 (1977), 321–325.
33. Marsaglia, G .; Цанг, В. В. (2000). «Простой метод генерации гамма-переменных». Транзакции ACM на математическом ПО. 26 (3): 363–372. Дои:10.1145/358407.358414. S2CID  2634158.

внешняя ссылка

• «Гамма-распределение», Энциклопедия математики, EMS Press, 2001 [1994]
• Вайсштейн, Эрик В. «Гамма-распределение». MathWorld.
• ModelAssist (2017) Использование гамма-распределения в моделировании рисков, включая прикладные примеры в Excel.
• Справочник по инженерной статистике