Теорема колокола - Bells theorem
Теорема Белла доказывает, что квантовая физика несовместимо с локальные теории скрытых переменных. Он был введен физиком Джон Стюарт Белл в статье 1964 года под названием «О Эйнштейн Подольский Парадокс Розена ", имея в виду 1935 г. мысленный эксперимент который Альберт Эйнштейн, Борис Подольский и Натан Розен привыкли утверждать, что квантовая физика - «неполная» теория.[1][2] К 1935 году уже было признано, что предсказания квантовой физики верны. вероятностный. Эйнштейн, Подольский и Розен представили сценарий, который, по их мнению, указывает на то, что квантовые частицы, такие как электроны и фотоны, должны нести физические свойства или атрибуты, не включенные в квантовую теорию, а неопределенности в предсказаниях квантовой теории были из-за незнания этих свойств, позже названных «скрытыми переменными». Их сценарий включает в себя пару широко разделенных физических объектов, подготовленных таким образом, что квантовое состояние пары это запутанный.
Белл продвинул анализ квантовой запутанности намного дальше. Он пришел к выводу, что если измерения выполняются независимо на двух разделенных половинах пары, то предположение о том, что результаты зависят от скрытых переменных в каждой половине, подразумевает ограничение на то, как коррелируются результаты на двух половинах. Это ограничение позже будет названо неравенством Белла. Затем Белл показал, что квантовая физика предсказывает корреляции, нарушающие это неравенство. Следовательно, единственный способ, которым скрытые переменные могли бы объяснить предсказания квантовой физики, - это если они являются «нелокальными», каким-то образом связаны с обеими половинами пары и способны мгновенно переносить влияния между ними, независимо от того, насколько широко разделены две половины.[3][4] Как позже писал Белл, «если [теория скрытых переменных] является локальной, она не будет согласована с квантовой механикой, а если она согласуется с квантовой механикой, она не будет локальной».[5]
В последующие годы были доказаны многочисленные вариации теоремы Белла, в которых были введены другие тесно связанные условия, обычно известные как неравенства Белла (или «неравенства типа Белла»). Это были испытано экспериментально в физических лабораториях много раз с 1972 года. Часто эти эксперименты преследовали цель облегчить проблемы экспериментального дизайна или установки, которые в принципе могли повлиять на достоверность результатов более ранних тестов Белла. Это известно как "закрытие лазейки в тестовых экспериментах Bell ". На сегодняшний день тесты Белла показали, что гипотеза о локальных скрытых переменных несовместима с тем, как фактически ведут себя физические системы.[6][7]
Точная природа предположений, необходимых для доказательства ограничения типа Белла на корреляции, обсуждалась физиками и исследователями. философы. Хотя значение теоремы Белла не вызывает сомнений, ее полное значение для интерпретация квантовой механики остаются нерешенными.
Историческое прошлое
В начале 1930-х годов философские последствия нынешних интерпретаций квантовой теории беспокоили многих выдающихся физиков того времени, включая Альберт Эйнштейн. В известной статье 1935 г. Борис Подольский и соавторы Эйнштейн и Натан Розен (совместно "EPR") стремились продемонстрировать Парадокс ЭПР что квантовая механика была неполной. Это давало надежду, что однажды может быть открыта более полная (и менее тревожная) теория. Но этот вывод основывался на, казалось бы, разумных предположениях местонахождение и реализм (вместе именуемые "местный реализм" или "локальные скрытые переменные ", часто взаимозаменяемо). На просторечии Эйнштейна: местонахождение не означал мгновенного ("жуткое") действие на расстоянии; реализм означал, что луна присутствует даже тогда, когда за ней не наблюдают. Эти предположения горячо обсуждались в физическом сообществе, особенно между Эйнштейном и Нильсом Бором.
В своей новаторской статье 1964 года "О парадоксе Эйнштейна-Подольского-Розена"[2][8] физик Джон Стюарт Белл представил дальнейшее развитие, основанное на вращение измерения на парах запутанных электронов гипотетического парадокса ЭПР. Используя их рассуждения, он сказал, что выбор настройки измерения поблизости не должен влиять на результат измерения вдали (и наоборот). После предоставления математической формулировки локальности и реализма, основанной на этом, он показал конкретные случаи, когда это не соответствовало бы предсказаниям квантовой механики.
В экспериментальных тестах по примеру Белла, теперь использующих квантовая запутанность фотонов вместо электронов, Джон Клаузер и Стюарт Фридман (1972) и Ален Аспект и другие. (1981) продемонстрировали, что предсказания квантовой механики верны в этом отношении, хотя и полагались на дополнительные непроверяемые предположения, которые открывают лазейки для местного реализма. Более поздние эксперименты помогли закрыть эти лазейки.[9][10]
Обзор
Эта секция слишком много внимания уделяется конкретным примерам без объясняя их важность к своей основной теме. (Июнь 2019) |
Теорема обычно доказывается рассмотрением квантовой системы двух запутанный кубиты с исходными тестами, как указано выше, выполненными на фотонах. Наиболее распространенные примеры касаются систем частиц, запутанных в вращение или же поляризация. Квантовая механика позволяет предсказывать корреляции, которые наблюдались бы, если бы спин или поляризация этих двух частиц измерялись в разных направлениях. Белл показал, что если верна теория локальных скрытых переменных, то эти корреляции должны удовлетворять определенным ограничениям, называемым неравенствами Белла.

Следуя аргументам в Парадокс Эйнштейна – Подольского – Розена (ЭПР) бумага (но на примере вращения, как в Дэвид Бом версия аргумента EPR[11]) Белл считал мысленный эксперимент в котором есть «пара спиновых половинных частиц, образованная каким-то образом в синглетное спиновое состояние и свободно перемещаясь в противоположных направлениях ".[2] Две частицы перемещаются друг от друга к двум удаленным точкам, в которых выполняются измерения вращения по осям, которые выбираются независимо. Каждый измерение дает результат либо увеличения (+), либо уменьшения (-); это означает вращение в положительном или отрицательном направлении выбранной оси.
Вероятность получения одного и того же результата в двух точках зависит от относительных углов, под которыми выполняются два измерения вращения, и находится строго между нулем и единицей для всех относительных углов, кроме идеально параллельных или антипараллельных совмещений (0 ° или 180 °. ). Поскольку полный угловой момент сохраняется, и поскольку полный спин равен нулю в синглетном состоянии, вероятность того же результата при параллельном (антипараллельном) выравнивании равна 0 (1). Это последнее предсказание верно как с классической, так и с квантовой механики.
Теорема Белла касается корреляций, определяемых в терминах средних значений, взятых во время очень многих попыток эксперимента. В корреляция двух бинарных переменных обычно определяется в квантовой физике как среднее значение произведений пар измерений. Обратите внимание, что это отличается от обычного определения корреляция в статистике. «Корреляция» квантового физика - это «сырой (нецентрированный, ненормализованный) продукт статистики». момент ". Они похожи в том, что при любом определении, если пары результатов всегда одинаковы, корреляция равна +1; если пары результатов всегда противоположны, корреляция равна -1; и если пары результатов совпадают В 50% случаев корреляция равна 0. Корреляция связана простым способом с вероятностью равных результатов, а именно, она равна удвоенной вероятности равных результатов минус один.
Измерение вращения этих запутанных частиц в антипараллельных направлениях (т. е. обращенных точно в противоположных направлениях, возможно, смещенных на какое-то произвольное расстояние) набор всех результатов идеально коррелирован. С другой стороны, если измерения выполняются в параллельных направлениях (т. Е. В одном и том же направлении, возможно, со смещением на какое-то произвольное расстояние), они всегда дают противоположные результаты, и набор измерений показывает идеальную антикорреляцию. Это согласуется с вышеупомянутой вероятностью измерения одного и того же результата в этих двух случаях. Наконец, измерения в перпендикулярных направлениях имеют 50% шанс совпадения, а общий набор измерений не коррелирован. Эти основные случаи показаны в таблице ниже. Столбцы следует читать как Примеры пар значений, которые могут быть записаны Алисой и Бобом, с увеличением времени вправо.
| Антипараллельный | Пара | ||||||
|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | ... | п | ||
| Алиса, 0° | + | − | + | + | ... | − | |
| Боб, 180° | + | − | + | + | ... | − | |
| Корреляция | ( +1 | +1 | +1 | +1 | ... | +1 ) | / п = +1 |
| (100% идентичны) | |||||||
| Параллельный | 1 | 2 | 3 | 4 | ... | п | |
| Алиса, 0° | + | − | − | + | ... | + | |
| Боб, 0 ° или 360 ° | − | + | + | − | ... | − | |
| Корреляция | ( −1 | −1 | −1 | −1 | ... | −1 ) | / п = −1 |
| (100% напротив) | |||||||
| Ортогональный | 1 | 2 | 3 | 4 | ... | п | |
| Алиса, 0 ° | + | − | + | − | ... | − | |
| Боб, 90 ° или 270 ° | − | − | + | + | ... | − | |
| Корреляция | ( −1 | +1 | +1 | −1 | ... | +1 ) | / п = 0 |
| (50% идентичны, 50% противоположны) | |||||||
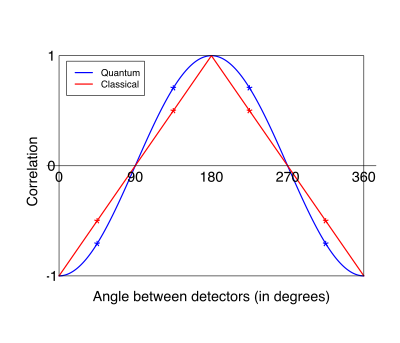
При измерениях, ориентированных под промежуточными углами между этими основными случаями, существование локальных скрытых переменных могло бы согласовываться с / было бы согласовано с линейной зависимостью корреляция в угле, но, согласно неравенству Белла (см. ниже), не мог согласиться с зависимостью, предсказанной квантовой теорией, а именно с тем, что корреляция является отрицательной косинус угла. Результаты экспериментов соответствуют кривой, предсказанной квантовой механикой.[3]
За прошедшие годы теорема Белла прошла множество экспериментальных проверок. Однако различные общие недостатки в проверке теоремы были выявлены, в том числе лазейка для обнаружения[12] и лазейка в коммуникации.[12] С годами эксперименты постепенно улучшались, чтобы лучше устранить эти лазейки. В 2015 году был проведен первый эксперимент по одновременному устранению всех лазеек.[9]
На сегодняшний день теорема Белла обычно считается подтвержденной значительным количеством доказательств, и есть несколько сторонников локальных скрытых переменных, хотя теорема постоянно является предметом изучения, критики и уточнения.[13][14]
Важность
Теорема Белла, выведенная в его основополагающей статье 1964 года под названием «О парадоксе Эйнштейна-Подольского-Розена»,[2] был назван, исходя из предположения, что теория верна, «самой глубокой в науке».[15] Возможно, не меньшее значение имеет преднамеренное усилие Белла по поощрению и легитимности работы над вопросами полноты, которая приобрела дурную славу.[16] Позже Белл выразил надежду, что такая работа «продолжит вдохновлять тех, кто подозревает, что доказательства невозможности доказывают недостаток воображения».[16] Н. Дэвид Мермин описал оценки важности теоремы Белла в физическом сообществе в диапазоне от «безразличия» до «дикой расточительности».[17] Генри Стэпп заявил: «Теорема Белла - самое глубокое открытие науки».[18]
Название основополагающей статьи Белла относится к статье 1935 г. Эйнштейн, Подольский и Розен[19] это поставило под сомнение полноту квантовой механики. В своей статье Белл исходил из тех же двух предположений, что и ЭПР, а именно (i) реальность (что микроскопические объекты обладают реальными свойствами, определяющими результаты квантово-механических измерений), и (ii) местонахождение (на реальность в одном месте не влияют измерения, выполняемые одновременно в удаленном месте). Белл смог получить из этих двух предположений важный результат, а именно неравенство Белла. Теоретическое (а затем и экспериментальное) нарушение этого неравенства означает, что хотя бы одно из двух предположений должно быть ложным.
В двух отношениях статья Белла 1964 года была шагом вперед по сравнению с бумагой ЭПР: во-первых, она рассматривала больше скрытые переменные чем просто элемент физической реальности в документе EPR; а неравенство Белла отчасти можно было проверить экспериментально, что повысило возможность проверки гипотезы локального реализма. Ограничения на такие испытания на сегодняшний день указаны ниже. В то время как статья Белла касается только детерминированных теорий скрытых переменных, теорема Белла позже была обобщена на стохастический теории[20] так же, и это тоже было реализовано[21] что теорема не столько о скрытых переменных, сколько о результатах измерений, которые можно было бы провести вместо того, что было действительно сделано. Существование этих переменных называется предположением реализма или предположением контрфактическая определенность.
После статьи ЭПР квантовая механика оказалась в неудовлетворительном положении: либо она была неполной в том смысле, что не могла учесть некоторые элементы физической реальности, либо нарушала принцип конечной скорости распространения физических эффектов. В модифицированной версии мысленного эксперимента EPR два гипотетических наблюдатели, теперь обычно называют Алиса и Боб, выполнить независимые измерения спина пары электронов, приготовленных в источнике в особом состоянии, называемом спин-синглет государственный. Это вывод ЭПР: как только Алиса измеряет вращение в одном направлении (например, на Икс ось), измерение Боба в этом направлении определяется с уверенностью, как результат, противоположный результату Алисы, тогда как непосредственно перед измерением Алисы результат Боба был определен только статистически (т.е.был только вероятностью, а не достоверностью); таким образом, либо вращение в каждом направлении является элемент физической реальности, или эффекты мгновенно переходят от Алисы к Бобу.
В QM прогнозы формулируются в терминах вероятности - например, вероятность того, что электрон будет обнаружен в определенном месте, или вероятность того, что его вращение будет вверх или вниз. Однако сохранялась идея, что электрон на самом деле имеет определенный положение и вращение, и слабость QM - его неспособность точно предсказать эти значения. Существовала возможность того, что какая-то неизвестная теория, такая как теория скрытых переменных, может быть в состоянии точно предсказать эти величины, в то же время находясь в полном согласии с вероятностями, предсказанными QM. Если такая теория скрытых переменных существует, то, поскольку скрытые переменные не описываются QM, последняя будет неполной теорией.
Местный реализм
Концепция локального реализма формализована, чтобы сформулировать и доказать теорему Белла и обобщения. Общий подход следующий:
- Существует вероятностное пространство Λ а результаты, наблюдаемые как Алисой, так и Бобом, являются результатом случайной выборки (неизвестного, «скрытого») параметра. λ ∈ Λ.
- Значения, наблюдаемые Алисой или Бобом, являются функциями настроек локального детектора, состояния входящего события (спин для материала или фазы для фотона) и только скрытого параметра. Таким образом, есть функции А,B : S2 × Λ → {-1, +1} , где установка детектора моделируется как положение на единичной сфере S2, так что
- Значение, наблюдаемое Алисой с настройкой детектора а является А(а, λ)
- Значение, наблюдаемое Бобом с настройкой детектора б является B(б, λ)
Для идеальной антикорреляции потребуется B(c, λ) = −А(c, λ), c ∈ S2. Неявно в предположении 1) выше скрытое пространство параметров Λ имеет вероятностная мера μ и ожидание случайной величины Икс на Λ относительно μ написано
где для доступности обозначений мы предполагаем, что вероятностная мера имеет плотность вероятности п что поэтому неотрицательно и интегрируется с 1. Скрытый параметр часто считается связанным с источником, но он также может содержать компоненты, связанные с двумя измерительными устройствами.
Неравенства Белла
Неравенства Белла касаются измерений, сделанных наблюдателями на парах частиц, которые взаимодействовали и затем разделялись. Предполагая локальный реализм, определенные ограничения должны удерживать взаимосвязи между корреляциями между последующими измерениями частиц при различных возможных параметрах измерения. Позволять А и B быть как указано выше. Определите для настоящих целей три корреляционные функции:
- Позволять Cе(а, б) обозначают экспериментально измеренную корреляцию, определяемую
- куда N++ - количество измерений, дающих "раскрутку" в направлении а измеряется Алисой (первый индекс +) и "раскручиваться" в сторону б измеряется Бобом. Другие случаи появления N определены аналогично. Другими словами, это выражение обозначает количество раз, когда Алиса и Боб обнаруживали одно и то же вращение, за вычетом количества раз, когда они находили противоположное вращение, деленное на общее количество измерений для данной пары углов.
- Позволять Cq(а, б) обозначают корреляцию, как предсказывает квантовая механика. Это дается выражением[нужна цитата ]
- куда - антисимметричная спиновая волновая функция, это Вектор Паули. Это значение рассчитывается как
- куда и являются единичными векторами, которые представляют каждое измерительное устройство и внутренний продукт равен косинусу угла между этими векторами.
- Позволять Cчас(а, б) обозначают корреляцию, как предсказывается любой теорией скрытых переменных. В формализации вышеизложенного это
Двухчастичное спиновое пространство - это тензорное произведение двумерных спиновых гильбертовых пространств отдельных частиц. Каждое отдельное пространство - это неприводимое пространство представления из группа вращения SO (3). Пространство произведения распадается как прямая сумма неприводимых представлений с определенными полными спинами 0 и 1 размеров 1 и 3 соответственно. Полную информацию можно найти в Разложение Клебша-Гордана. Подпространство с нулевым полным спином натянуто на синглетное состояние в пространстве продукта вектор, явно заданный формулой
с присоединенным в этом представлении
То, как операторы одиночной частицы действуют в пространстве продукта, показано ниже на рассматриваемом примере; определяется тензорное произведение операторов, где множители являются одночастичными операторами, таким образом, если Π, Ω одночастичные операторы,
и
и т.д., где верхний индекс в круглых скобках указывает, на каком гильбертовом пространстве в пространстве тензорного произведения предполагается действие, а действие определяется правой частью. Синглетное состояние имеет полный спин 0 что может быть проверено применением оператора полного спина J · J = (J1 + J2) ⋅ (J1 + J2) расчетом, аналогичным представленному ниже.
Математическое ожидание оператора
в синглетном состоянии можно рассчитать напрямую. По определению Матрицы Паули,
После оставленного применения этого на |А⟩ можно получить
Аналогично, приложение (слева) оператора, соответствующего б на ⟨А| дает
Скалярные произведения в пространстве тензорных произведений определяются как
Учитывая это, математическое ожидание уменьшается до
С помощью этих обозначений можно сделать краткое изложение того, что следует ниже.
- Теоретически существует а, б такой, что
- каковы бы ни были конкретные характеристики теории скрытых переменных, пока она подчиняется правилам местного реализма, как определено выше. Другими словами, никакая теория локальных скрытых переменных не может делать таких же предсказаний, как квантовая механика.
- Экспериментально экземпляры
- были обнаружены (независимо от теории скрытых переменных), но
- никогда не был найден. То есть предсказания квантовой механики никогда не опровергались экспериментом. Эти эксперименты включают такие, которые могут исключить теории локальных скрытых переменных. Но смотрите ниже о возможных лазейках.
Оригинальное неравенство Белла
Неравенство, полученное Беллом, можно записать как:[2]
куда а, б и c относятся к трем произвольным настройкам двух анализаторов. Однако это неравенство ограничено в своем применении довольно частным случаем, в котором результаты обеих сторон эксперимента всегда точно антикоррелированы, когда анализаторы параллельны. Преимущество ограничения внимания этим частным случаем заключается в простоте вывода. В экспериментальной работе неравенство не очень полезно, потому что его трудно, если не невозможно, создать. идеально антикорреляция.
Однако у этой простой формы есть интуитивное объяснение. Это эквивалентно следующему элементарному результату теории вероятностей. Рассмотрим три (сильно коррелированных и, возможно, предвзятых) подбрасывания монеты X, Y, и Z, со свойством, которое:
- Икс и Y дают одинаковый результат (обе решки или орла) в 99% случаев
- Y и Z также дают тот же результат в 99% случаев,
тогда Икс и Z должен также давать тот же результат, по крайней мере, в 98% случаев. Количество несоответствий между Икс и Y (1/100) плюс количество несовпадений между Y и Z (1/100) вместе максимально возможное количество несоответствий между Икс и Z (простой Неравенство Буля – Фреше. ).
Представьте себе пару частиц, которые можно измерить в удаленных местах. Предположим, что у измерительных устройств есть настройки, которыми являются углы, например, устройства измеряют что-то, называемое вращением, в каком-то направлении. Экспериментатор выбирает направления, по одному для каждой частицы, отдельно. Предположим, результат измерения двоичный (например, увеличение или уменьшение скорости). Предположим, что две частицы совершенно антикоррелированы - в том смысле, что всякий раз, когда обе частицы измеряются в одном направлении, одна получает идентично противоположные результаты, когда обе частицы измеряются в противоположных направлениях, они всегда дают одинаковый результат. Единственный способ представить, как это работает, - это то, что обе частицы покидают свой общий источник, каким-то образом с теми результатами, которые они дадут при измерении в любом возможном направлении. (Как еще частица 1 могла знать, как дать тот же ответ, что и частица 2, при измерении в том же направлении? Они не знают заранее, как они будут измеряться ...). Измерение частицы 2 (после смены ее знака) можно рассматривать как показание того, что дало бы то же измерение частицы 1.
Начните с одной настройки, прямо противоположной другой. Все пары частиц дают один и тот же результат (каждая пара имеет либо вращение вверх, либо вращение вниз). Теперь сместите настройку Алисы на один градус относительно настройки Боба. Теперь они на один градус отстают друг от друга. Небольшая часть пар, скажем, ж-А теперь дают разные результаты. Если бы вместо этого мы оставили настройку Алисы без изменений, но сместили настройку Боба на один градус (в противоположном направлении), то снова на дробную часть. ж пар частиц дает разные результаты. Наконец, подумайте, что происходит, когда обе смены выполняются одновременно: две настройки теперь находятся ровно в двух градусах от того, чтобы быть противоположными друг другу. Согласно аргументу несоответствия, вероятность несоответствия в двух степенях не может быть более чем в два раза выше шанса несоответствия в одной степени: она не может быть больше двух.ж.
Сравните это с предсказаниями квантовой механики для синглетного состояния. Для небольшого угла θ, измеряемая в радианах, вероятность другого результата составляет приблизительно как объяснил малоугловое приближение. Таким образом, при двукратном увеличении этого малого угла вероятность несоответствия примерно в 4 раза больше, поскольку . Но мы просто утверждали, что он не может быть больше, чем в 2 раза.
Эта интуитивно понятная формулировка обусловлена Дэвид Мермин. Малоугловой предел обсуждается в оригинальной статье Белла и, следовательно, восходит к истокам неравенств Белла.[нужна цитата ]
ЧШ неравенство
Обобщая исходное неравенство Белла,[2] Джон Клаузер, Майкл Хорн, Эбнер Шимони и Р. А. Холт представили ЧШ неравенство,[22] который ставит классические ограничения на набор из четырех корреляций в эксперименте Алисы и Боба, без каких-либо предположений об идеальных корреляциях (или антикорреляциях) при одинаковых настройках.
Особый выбор , обозначая , и предполагая идеальную антикорреляцию при одинаковых настройках, идеальную корреляцию при противоположных настройках, поэтому и , неравенство CHSH сводится к исходному неравенству Белла. В настоящее время (1) также часто называют просто «неравенством Белла», но иногда более полно «неравенством Белла-ЧШШ».
Вывод классической оценки
С сокращенными обозначениями
неравенство CHSH можно вывести следующим образом. Каждая из четырех величин равна и каждый зависит от . Отсюда следует, что для любого , один из и равен нулю, а другой . Из этого следует, что
и поэтому
В основе этого вывода лежит простое алгебраическое неравенство относительно четырех переменных: , которые принимают значения Только:
Неравенство CHSH зависит только от следующих трех ключевых характеристик теории локальных скрытых переменных: (1) реализм: наряду с результатами фактически выполненных измерений, результаты потенциально выполненных измерений также существуют в то же время; (2) локальность, результаты измерений частицы Алисы не зависят от того, какое измерение Боб выбирает для другой частицы; (3) свобода: Алиса и Боб действительно могут свободно выбирать, какие измерения проводить.
В реализм предположение на самом деле является несколько идеалистическим, и теорема Белла доказывает нелокальность только по отношению к переменным, которые только существовать по метафизическим причинам[нужна цитата ]. Однако до открытия квантовой механики и реализм, и локальность были совершенно бесспорными чертами физических теорий.
Предсказания квантовой механики нарушают неравенства CHSH
Измерения, выполненные Алисой и Бобом, являются измерениями спина электронов. Алиса может выбрать одну из двух настроек детектора, помеченных и ; эти настройки соответствуют измерению вращения вдоль или ось. Боб может выбрать одну из двух настроек детектора, помеченных и ; они соответствуют измерению спина вдоль или же ось, где система координат повернута на 135 ° относительно система координат. Спиновые наблюдаемые представлены самосопряженными матрицами 2 × 2:
Эти Спиновые матрицы Паули, которые, как известно, имеют собственные значения, равные . Как обычно, будем использовать обозначение бюстгальтера для обозначения собственных векторов в качестве , куда
Согласно квантовой механике, выбор измерений закодирован в выборе эрмитовых операторов, применяемых к этому состоянию. В частности, рассмотрите следующие операторы:
куда представляют два варианта измерения Алисы, и два варианта измерения Боба.
Чтобы получить математическое ожидание, данное при данном выборе измерения Алисы и Боба, необходимо вычислить математическое ожидание соответствующей пары операторов (например, если входы выбраны ) над общим состоянием .
Например, математическое ожидание соответствует Алисе, выбирающей параметр измерения и Боб выбирает параметры измерения вычисляется как
Теорема Белла: если квантово-механический формализм верен, то система, состоящая из пары запутанных электронов, не может удовлетворять принципу локального реализма. Обратите внимание, что действительно, верхняя граница квантовой механики называется Связка Цирельсона. Операторы, дающие это максимальное значение, всегда изоморфный к матрицам Паули.[23]
Проверка практическими экспериментами
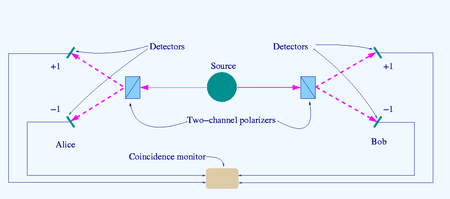
Источник S производит пары «фотонов», посылаемые в противоположных направлениях. Каждый фотон встречает двухканальный поляризатор, ориентация которого (a или b) может быть установлена экспериментатором. Сигналы, появляющиеся из каждого канала, обнаруживаются и совпадения четырех типов (++, −−, + - и - +) подсчитываются монитором совпадений.
Экспериментальные тесты могут определить, соответствуют ли неравенства Белла, требуемые местным реализмом, эмпирическим данным.
Фактически, большинство экспериментов проводилось с использованием поляризации фотонов, а не спина электронов (или других частиц со спином половинной длины). Квантовое состояние пары запутанных фотонов не является синглетным состоянием, и соответствие между углами и исходами отличается от такового в установке со спином половины. Поляризация фотона измеряется в паре перпендикулярных направлений. Относительно данной ориентации поляризация бывает вертикальной (обозначается V или +) или горизонтальной (обозначается H или -). Фотонные пары генерируются в квантовом состоянии
куда и означает состояние одного вертикально или горизонтально поляризованного фотона, соответственно (по отношению к фиксированной и общим опорным направлением для обеих частиц).
Когда поляризация обоих фотонов измеряется в одном направлении, оба дают один и тот же результат: идеальную корреляцию. При измерении в направлениях, составляющих угол 45 ° друг с другом, результаты полностью случайны (некоррелированы). Измеряя в направлениях под углом 90 ° друг к другу, эти два изображения идеально антикоррелированы. В общем, когда поляризаторы расположены под углом θ друг к другу корреляция cos (2θ). Таким образом, относительно корреляционной функции для синглетного состояния спиновых половинных частиц у нас есть положительная, а не отрицательная функция косинуса, а углы уменьшены вдвое: корреляция периодична с периодом π вместо 2π.
Неравенства Белла проверяются «подсчетом совпадений» из тестового эксперимента Белла, такого как оптический, показанный на диаграмме. Пары частиц испускаются в результате квантового процесса, анализируются в отношении некоторых ключевых свойств, таких как направление поляризации, а затем обнаруживаются. Установку (ориентацию) анализаторов выбирает экспериментатор.
На сегодняшний день тестовые эксперименты Белла в подавляющем большинстве нарушают неравенство Белла.
Два класса неравенств Белла
В проблема честной выборки открыто столкнулись в 1970-х. В ранних планах эксперимента 1973 года Фридман и Клаузер[24] использовал честная выборка в виде формулы Клаузера – Хорна – Шимони – Холта (CHSH[22]) гипотеза. Однако вскоре после этого Клаузер и Хорн[20] сделали важное различие между неоднородными (IBI) и однородными (HBI) неравенствами Белла. Тестирование IBI требует, чтобы мы сравнили определенные скорости совпадения в двух отдельных детекторах с одиночными скоростями двух детекторов. Никто не нуждался в проведении эксперимента, потому что одиночные ставки со всеми детекторами в 1970-х годах как минимум в десять раз превышали все уровни совпадений. Итак, принимая во внимание такую низкую эффективность детектора, предсказание QM фактически удовлетворило IBI. Чтобы прийти к экспериментальному плану, в котором предсказание КМ нарушает IBI, нам необходимы детекторы, эффективность которых превышает 82,8% для синглетных состояний,[25] но имеют очень низкий уровень темноты и короткое время простоя и разрешения. Однако Эберхард (1976) обнаружил, что с вариантом неравенства Клаузера-Хорна и с использованием менее чем максимально запутанных состояний требуется только 66,67% эффективности обнаружения. Это было достигнуто в 2015 году с помощью двух успешных экспериментов типа Белла «без лазеек» в Вене (Джустина и др.) И в NIST в Боулдере, Колорадо (Шалм и др.) [Ссылки будут добавлены].
Практические задачи
Потому что в то время даже лучшие детекторы не регистрировали большую часть всех фотонов, Клаузер и Хорн[20] признал, что проверка неравенства Белла требует некоторых дополнительных предположений. Они представили Гипотеза об отсутствии улучшения (NEH):
Световой сигнал, исходящий из атомный каскад например, имеет определенную вероятность срабатывания детектора. Тогда, если между каскадом и детектором установить поляризатор, вероятность обнаружения не может увеличиться.
При этом предположении существует неравенство Белла между частотами совпадений с поляризаторами и частотами совпадений без поляризаторов.
Эксперимент проводили Фридман и Клаузер,[24] который обнаружил, что неравенство Белла было нарушено. Таким образом, гипотеза об отсутствии улучшения не может быть верной в модели локальных скрытых переменных.
В то время как в ранних экспериментах использовались атомные каскады, в более поздних экспериментах использовалось параметрическое преобразование с понижением частоты, следуя предложению Рейда и Уоллса,[26] дает улучшенные свойства генерации и обнаружения. В результате недавние эксперименты с фотонами больше не страдают от лазейки для обнаружения. Это сделало фотон первой экспериментальной системой, для которой были преодолены все основные экспериментальные лазейки, хотя сначала только в отдельных экспериментах. С 2015 г. экспериментаторы смогли преодолеть все основные экспериментальные лазейки одновременно; видеть Белл тестовые эксперименты.
Интерпретации теоремы Белла
Большинство сторонников идеи скрытых переменных считают, что эксперименты исключили локальные скрытые переменные. Они готовы отказаться от локальности, объясняя нарушение неравенства Белла нелокальным теория скрытых переменных, в котором частицы обмениваются информацией о своем состоянии. Это основа Интерпретация Бома квантовой механики, которая требует, чтобы все частицы во Вселенной могли мгновенно обмениваться информацией со всеми остальными. Эксперимент 2007 года исключил большой класс небомовских нелокальных теорий скрытых переменных.[27]
Транзакционная интерпретация квантовой механики
Если скрытые переменные могут взаимодействовать друг с другом быстрее света, неравенство Белла может быть легко нарушено. После измерения одной частицы она может передать необходимые корреляции другой частице. Поскольку в теории относительности понятие одновременности не является абсолютным, это непривлекательно. Одна из идей состоит в том, чтобы заменить мгновенное общение процессом, который перемещается в прошлое во времени. световой конус. Это идея транзакционная интерпретация квантовой механики, которая интерпретирует статистическое появление квантовой истории как постепенное достижение согласия между историями, идущими как вперед, так и назад во времени.[28]
Многомировая интерпретация квантовой механики
В Многимировая интерпретация является локальным и детерминированным, поскольку состоит из единой части квантовой механики без коллапса. Он может генерировать корреляции, которые нарушают неравенство Белла, поскольку не удовлетворяют неявному предположению, сделанному Беллом, что измерения имеют единственный результат. Фактически, теорема Белла может быть доказана в рамках многомировой системы из предположения, что измерение имеет единственный результат. Следовательно, нарушение неравенства Белла можно интерпретировать как демонстрацию того, что измерения имеют несколько результатов.[29]
Корреляции Белла объясняются тем, что когда Алиса и Боб проводят измерения, они разделяются на локальные ветви. С точки зрения каждой копии Алисы, существует несколько копий Боба с разными результатами, поэтому у Боба не может быть определенного результата, и то же самое верно с точки зрения каждой копии Боба. Они получат взаимно определенный результат только тогда, когда их будущие световые конусы будут перекрывать друг друга. С этого момента мы можем сказать, что корреляция Белла начинает существовать, но она была произведена чисто локальным механизмом. Следовательно, нарушение неравенства Белла нельзя интерпретировать как доказательство нелокальности.[30]
Супердетерминизм
Сам Белл резюмировал один из возможных способов решения теоремы: супердетерминизм в интервью Радио Би-би-си 1985 года:
Есть способ избежать вывода сверхсветовой скорости и жуткие действия на расстоянии. Но это предполагает абсолютное детерминизм во Вселенной полное отсутствие свободная воля. Предположим, что мир супердетерминирован, в нем не только неодушевленная природа работает на закулисных часах, но и наше поведение, включая нашу веру в то, что мы вправе проводить один эксперимент, а не другой, абсолютно предопределенный, включая решение экспериментатора провести одну серию измерений, а не другую, трудность исчезает. Нет необходимости в сигнале, превышающем скорость света, чтобы сообщить частице А какое измерение было выполнено на частицеB, потому что Вселенная, включая частицуА, уже «знает», каким будет это измерение и его результат.[31]
Некоторые сторонники детерминированных моделей не отказались от локальных скрытых переменных. Например, Жерар т Хофт утверждал, что вышеупомянутый супердетерминизм лазейку нельзя сбрасывать со счетов.[32] Для теория скрытых переменных, если условия Белла верны, результаты, согласующиеся с квантово-механической теорией, по-видимому, указывают сверхсветовой (быстрее света) эффекты, в отличие от релятивистская физика.
Также неоднократно заявлялось, что аргументы Белла неуместны, потому что они зависят от скрытых предположений, которые на самом деле сомнительны. Например, Э. Т. Джейнс[33] В 1989 г. утверждал, что в теореме Белла есть два скрытых предположения, ограничивающих ее общность. По словам Джейнса:
- Белл интерпретировал условную вероятность п(Икс | Y) как причинное влияние, т.е. Y оказал причинное влияние на Икс в действительности. Эта интерпретация является неправильным пониманием теории вероятностей. Как показывает Джейнс,[33] «невозможно даже правильно рассуждать в такой простой задаче, как вытаскивание двух шаров из урны Бернулли, если он интерпретирует вероятности таким образом».
- Неравенство Белла неприменимо к некоторым возможным теориям скрытых переменных. Это применимо только к определенному классу теорий локальных скрытых переменных. Фактически, он мог просто упустить те теории скрытых переменных, которые больше всего интересуют Эйнштейна.
Ричард Д. Гилл утверждал, что Джейнс неправильно понял анализ Белла. Гилл отмечает, что в том же томе конференции, в котором Джейнс выступает против Белла, Джейнс признается, что был чрезвычайно впечатлен коротким доказательством Стив Галл представили на той же конференции, что синглетные корреляции не могут быть воспроизведены с помощью компьютерного моделирования теории локальных скрытых переменных.[34] По словам Джейнса (написавшего почти через 30 лет после выдающегося вклада Белла), нам, вероятно, понадобится еще 30 лет, чтобы полностью оценить потрясающий результат Галла.
В 2006 г. возникла волна активности по поводу последствий детерминизма. Джон Хортон Конвей и Саймон Б. Кочен с теорема о свободе воли,[35] в котором говорилось, что «реакция частицы со спином 1 на тройной эксперимент свободна, то есть не является функцией свойств той части Вселенной, которая предшествует этому отклику по отношению к любой данной инерциальной системе отсчета».[36] Эта теорема повысила осведомленность о противоречии между детерминизмом, полностью управляющим экспериментом (с одной стороны), и свободой Алисы и Боба выбирать любые настройки для своих наблюдений (с другой).[37][38] Философ Дэвид Ходжсон поддерживает эту теорему, показывая, что детерминизм ненаучный, тем самым оставляя дверь открытой для нашей собственной воли.[39]
Основные пометки
Нарушения неравенств Белла из-за квантовой запутанности обеспечивают почти окончательные демонстрации того, о чем уже сильно подозревали: что квантовая физика не может быть представлена какой-либо версией классической картины физики.[40] Некоторые ранние элементы, которые казались несовместимыми с классическими картинами, включали взаимодополняемость и коллапс волновой функции. Нарушения Белла показывают, что никакое решение таких проблем не может избежать крайней странности квантового поведения.[41]
Бумага EPR «указала на необычные свойства запутанные состояния, например вышеупомянутое синглетное состояние, которое является основой для современных приложений квантовой физики, таких как квантовая криптография; одно приложение включает измерение квантовой запутанности как физического источника битов для Рабина не обращая внимания на передачу протокол. Эта нелокальность изначально предполагалась иллюзорной, потому что стандартная интерпретация могла легко избавиться от действия на расстоянии, просто присвоив каждой частице определенные спиновые состояния для всех возможных направлений вращения. Аргумент ЭПР заключался в следующем: следовательно, эти определенные состояния существуют, следовательно, квантовая теория неполна в смысле ЭПР, поскольку они не появляются в теории. Теорема Белла показала, что предсказание квантовой механики о "запутанности" имеет степень нелокальности, которую нельзя объяснить ни одной классической теорией локальных скрытых переменных.
В теореме Белла сильна то, что она не относится ни к какой конкретной теории локальных скрытых переменных. Это показывает, что природа нарушает самые общие предположения, лежащие в основе классических картинок, а не только детали некоторых конкретных моделей. Никакая комбинация локальных детерминированных и локальных случайных скрытых переменных не может воспроизвести явления, предсказываемые квантовой механикой и неоднократно наблюдаемые в экспериментах.[42]
Смотрите также
- Мысленные эксперименты Эйнштейна
- Эпистемологические письма
- Фундаментальная Группа Фысикс
- GHZ эксперимент
- Теорема Глисона
- Теорема Кохена – Шпекера
- Неравенство леггетта
- Неравенство Леггетта – Гарга
- Измерение в квантовой механике
- Проблема Мотта
- PBR теорема
- Квантовая контекстуальность
- Квантовая нелокальность
- Эксперимент Реннингера с отрицательным результатом
Примечания
- ^ Эйнштейн, А.; Подольский, Б.; Розен, Н. (1935-05-15). «Можно ли считать квантово-механическое описание физической реальности полным?». Физический обзор. 47 (10): 777–780. Bibcode:1935ПхРв ... 47..777Э. Дои:10.1103 / PhysRev.47.777.
- ^ а б c d е ж Белл, Дж. С. (1964). "О парадоксе Эйнштейна Подольского и Розена" (PDF). Физика Телосложение Физика. 1 (3): 195–200. Дои:10.1103 / PhysicsPhysiqueFizika.1.195.
- ^ а б Паркер, Сибил Б. (1994). Энциклопедия физики Макгроу-Хилла (2-е изд.). Макгроу-Хилл. п.542. ISBN 978-0-07-051400-3.
- ^ Мермин, Н. Давид (Июль 1993 г.). «Скрытые переменные и две теоремы Джона Белла» (PDF). Обзоры современной физики. 65 (3): 803–15. arXiv:1802.10119. Bibcode:1993РвМП ... 65..803М. Дои:10.1103 / RevModPhys.65.803. S2CID 119546199.
- ^ Белл, Джон С. (1987). Разговорчивый и непроизносимый в квантовой механике. Издательство Кембриджского университета. п. 65. ISBN 9780521368698. OCLC 15053677.
- ^ The BIG Bell Test Collaboration (9 мая 2018 г.). «Бросить вызов местному реализму человеческим выбором». Природа. 557 (7704): 212–216. arXiv:1805.04431. Bibcode:2018Натура.557..212Б. Дои:10.1038 / s41586-018-0085-3. PMID 29743691. S2CID 13665914.
- ^ Вулховер, Натали (2017-02-07). «Эксперимент подтверждает квантовую странность». Журнал Quanta. Получено 2020-02-08.
- ^ Перепечатано в Дж. С. Белл (2004). «Глава 2: О парадоксе Эйнштейна-Подольского-Розена». Разговорчивый и невыразимый в квантовой механике: сборник статей по квантовой философии (Введение Алена Аспекта к изданию 1987 г.). Издательство Кембриджского университета. С. 14–21. ISBN 978-0521523387.
- ^ а б Hensen, B; Bernien, H; Dréau, AE; Райзерер, А; Kalb, N; Блок М.С. Ruitenberg, J; Вермёлен, РФ; Schouten, RN; Абеллан, К; Амая, Вт; Pruneri, V; Митчелл, штат МВт; Маркхэм, М; Твитчен, диджей; Elkouss, D; Венер, S; Таминиау, штат TH; Хэнсон, Р. (2015). «Нарушение неравенства Белла без петель с использованием электронных спинов, разделенных расстоянием 1,3 километра». Природа. 526 (7575): 682–686. arXiv:1508.05949. Bibcode:2015Натура.526..682H. Дои:10.1038 / природа15759. PMID 26503041. S2CID 205246446.
- ^ Зея Мерали (27.08.2015). «Квантовая« жуткость »проходит самое сложное испытание». Природа. 525 (7567): 14–15. Bibcode:2015Натура 525 ... 14 млн. Дои:10.1038 / природа.2015.18255. PMID 26333448.
- ^ Бом, Дэвид (1951). Квантовая теория. Прентис-Холл.
- ^ а б Статья о Теорема Белла Эбнер Шимони в Стэнфордская энциклопедия философии, (2004).
- ^ Гриффитс, Дэвид Дж. (1998). Введение в квантовую механику (2-е изд.). Пирсон /Prentice Hall. п. 423.
- ^ Мерцбахер, Евгений (2005). Квантовая механика (3-е изд.). Джон Уайли и сыновья. С. 18, 362.
- ^ Стэпп 1975
- ^ а б Белл, Дж. С. (1982). «На невозможной пилотной волне» (PDF). Основы физики. 12 (10): 989–99. Bibcode:1982ФоФ ... 12..989Б. Дои:10.1007 / bf01889272. S2CID 120592799. Перепечатано в Разговорчивый и невыразимый в квантовой механике: сборник статей по квантовой философии. Издательство Кембриджского университета, 2004 г., стр. 160.
- ^ Мермин, Дэвид (Апрель 1985 г.). «Есть ли луна там, где никто не смотрит? Реальность и квантовая теория» (PDF). Физика сегодня. 38 (4): 38–47. Bibcode:1985ФТ .... 38д..38М. Дои:10.1063/1.880968.
- ^ Стапп, Генри П. (1975). «Теорема Белла и мировой процесс». Nuovo Cimento. 29B (2): 270–276. Bibcode:1975NCimB..29..270S. Дои:10.1007 / BF02728310. S2CID 117358907. (Цитата на с. 271)
- ^ Эйнштейн, А .; Подольский, Б .; Розен, Н. (1935). «Можно ли считать квантово-механическое описание физической реальности полным?» (PDF). Физический обзор. 47 (10): 777–780. Bibcode:1935ПхРв ... 47..777Э. Дои:10.1103 / PhysRev.47.777.
- ^ а б c Клаузер, Джон Ф. (1974). «Экспериментальные следствия объективных локальных теорий» (PDF). Физический обзор D. 10 (2): 526–535. Bibcode:1974ПхРвД..10..526С. Дои:10.1103 / PhysRevD.10.526. Архивировано из оригинал (PDF) на 2013-12-25.
- ^ Эберхард, П. Х. (1977). «Теорема Белла без скрытых переменных» (PDF). Nuovo Cimento B. 38 (1): 75–80. arXiv:Quant-ph / 0010047. Bibcode:1977NCimB..38 ... 75E. CiteSeerX 10.1.1.252.6568. Дои:10.1007 / BF02726212. S2CID 51759163.
- ^ а б Клаузер, Джон; Хорн, Майкл; Шимони, Абнер; Холт, Ричард (1969). «Предлагаемый эксперимент для проверки локальных теорий скрытых переменных». Письма с физическими проверками. 23 (15): 880–884. Bibcode:1969ПхРвЛ..23..880С. Дои:10.1103 / PhysRevLett.23.880. S2CID 18467053.
- ^ Вернер, Рейнхард Ф .; Вольф, Майкл М. (2001). «Колокол неравенства и запутанность». Квантовая информация и вычисления. 1 (3): 1–25. arXiv:Quant-ph / 0107093. Bibcode:2001квант.ч..7093Вт. (Раздел 5.3 «Операторы максимального нарушения».) Саммерс, Стивен Дж .; Вернер, Рейнхард Ф. (1987). «Неравенства Белла и квантовая теория поля. I. Общие положения». Журнал математической физики. 28 (10): 2440–2447. Bibcode:1987JMP .... 28.2440S. Дои:10.1063/1.527733. (Стр. 2442.) См. Также: Цирельсон Борис (1987). «Квантовые аналоги неравенств Белла. Случай двух пространственно разделенных областей». Журнал советской математики. 36 (4): 557–570. Дои:10.1007 / BF01663472. S2CID 119363229. (Раздел 3 «Представление экстремальных корреляций».)
- ^ а б Фридман, Стюарт Дж .; Клаузер, Джон Ф. (1972). «Экспериментальная проверка локальных теорий скрытых переменных» (PDF). Письма с физическими проверками. 28 (14): 938–941. Bibcode:1972ПхРвЛ..28..938Ф. Дои:10.1103 / PhysRevLett.28.938. Архивировано из оригинал (PDF) на 2013-06-28. Получено 2013-12-24.
- ^ Гарг, Анупам; Н. Д. Мермин (1987), "Неэффективность детекторов в эксперименте Эйнштейна-Подольского-Розена", Phys. Ред. D, 25 (12): 3831–5, Bibcode:1987ПхРвД..35.3831Г, Дои:10.1103 / PhysRevD.35.3831, PMID 9957644
- ^ Рид, М.Д.; Уоллс, Д. Ф. (1986). «Нарушения классических неравенств в квантовой оптике». Физический обзор A. 34 (2): 1260–1276. Bibcode:1986ПхРвА..34.1260Р. Дои:10.1103 / PhysRevA.34.1260. PMID 9897387.
- ^ Грёблахер, Симон; Патерек, Томаш; Кальтенбек, Райнер; Брукнер, Часлав; Луковски, Марек; Аспельмейер, Маркус; Цайлингер, Антон (2007). «Экспериментальная проверка нелокального реализма». Природа. 446 (7138): 871–5. arXiv:0704.2529. Bibcode:2007Натура 446..871Г. Дои:10.1038 / природа05677. PMID 17443179. S2CID 4412358.
- ^ Крамер, Джон (1986). «Транзакционная интерпретация квантовой механики». Обзоры современной физики. 58 (3): 647–687. Bibcode:1986РвМП ... 58..647С. Дои:10.1103 / RevModPhys.58.647.
- ^ Дэвид Дойч; Патрик Хайден (200). «Информационный поток в запутанных квантовых системах». Труды Королевского общества А. 456 (1999): 1759–1774. arXiv:Quant-ph / 9906007. Bibcode:2000RSPSA.456.1759D. Дои:10.1098 / rspa.2000.0585. S2CID 13998168.
- ^ Харви Р. Браун; Кристофер Г. Тимпсон (2016). "Белл о теореме Белла: изменяющееся лицо нелокальности". В Мэри Белл; Шан Гао (ред.). Квантовая нелокальность и реальность: 50 лет теореме Белла. Издательство Кембриджского университета. С. 91–123. arXiv:1501.03521. Дои:10.1017 / CBO9781316219393.008. ISBN 9781316219393. S2CID 118686956.
- ^ Цитата представляет собой адаптацию отредактированной записи радиоинтервью с Джоном Беллом 1985 года. Призрак в атоме: обсуждение тайн квантовой физики, Пол С. В. Дэвис и Джулиан Р. Браун, 1986/1993, стр. 45-46
- ^ 'т Хоофт, Джерард (2016). Интерпретация квантовой механики клеточным автоматом. Фундаментальные теории физики. 185. Springer. Дои:10.1007/978-3-319-41285-6. ISBN 978-3-319-41284-9. OCLC 951761277. S2CID 7779840.
- ^ а б Джейнс, Э. Т. (1989). «Раскрытие тайн - изначальная цель». Раскрытие тайн - изначальная цель (PDF). Максимальная энтропия и байесовские методы. С. 1–27. CiteSeerX 10.1.1.46.1264. Дои:10.1007/978-94-015-7860-8_1. ISBN 978-90-481-4044-2.
- ^ Гилл, Ричард Д. (2003). «Время, конечная статистика и пятая позиция Белла». Proc. «Основы теории вероятностей и физики - 2», сер. Математика. Моделирование в Phys., Engin. И Cogn. Sc. 5/2002: 179–206. arXiv:Quant-ph / 0301059. Bibcode:2003квант.ч..1059Г.
- ^ Конвей, Джон; Кочен, Симон (2006). «Теорема о свободе воли». Основы физики. 36 (10): 1441–1473. arXiv:Quant-ph / 0604079. Bibcode:2006FoPh ... 36.1441C. Дои:10.1007 / s10701-006-9068-6. S2CID 12999337.
- ^ Конвей, Джон Х.; Кочен, Симон (2009). "Теорема сильной свободы воли" (PDF). Уведомления AMS. 56 (2): 226–232. arXiv:0807.3286. Bibcode:2008arXiv0807.3286C.
- ^ Катор, Эрик и Клаас Ландсман (2014). «Ограничения на детерминизм: Белл против Конвея – Кохена». Основы физики. 44 (7): 781–791. arXiv:1402.1972. Bibcode:2014FoPh ... 44..781C. Дои:10.1007 / s10701-014-9815-z. S2CID 14532489.
- ^ Эсфельд, Майкл (2015). «Теорема Белла и проблема детерминизма и индетерминизма». Основы физики. 45 (5): 471–482. arXiv:1503.00660. Bibcode:2015ФоФ ... 45..471E. Дои:10.1007 / s10701-015-9883-8. S2CID 49363278.
- ^ Дэвид Ходжсон (2012). «Глава 7: Наука и детерминизм». Рациональность + Сознание = Свобода Воли. Издательство Оксфордского университета. ISBN 9780199845309.
- ^ Пенроуз, Роджер (2007). Дорога к реальности. Винтажные книги. п. 583. ISBN 978-0-679-77631-4.
- ^ Аберс, Э. (2004). Квантовая механика. Эддисон Уэсли. С. 193–195. ISBN 9780131461000.
- ^ R.G. Лернер; Г.Л. Тригг (1991). Энциклопедия физики (2-е изд.). Издатели СКЗ. п.495. ISBN 978-0-89573-752-6.
Рекомендации
- Aspect, A .; и другие. (1981). «Экспериментальная проверка реалистичных локальных теорий с помощью теоремы Белла». Phys. Rev. Lett. 47 (7): 460–463. Bibcode:1981ПхРвЛ..47..460А. Дои:10.1103 / Physrevlett.47.460.
- Aspect, A .; и другие. (1982). "Экспериментальная реализация геданкенэксперимента Эйнштейна – Подольского – Розена – Бома: новое нарушение неравенств Белла". Phys. Rev. Lett. 49 (2): 91–94. Bibcode:1982ПхРвЛ..49 ... 91А. Дои:10.1103 / Physrevlett.49.91.
- Aspect, A .; и другие. (1982). «Экспериментальная проверка неравенств Белла с использованием нестационарных анализаторов». Phys. Rev. Lett. 49 (25): 1804–1807. Bibcode:1982ПхРвЛ..49.1804А. Дои:10.1103 / Physrevlett.49.1804.
- Aspect, A .; Гранжье, П. (1985). «О резонансном рассеянии и других гипотетических эффектах в атомно-каскадном эксперименте Орсе, проверяющем неравенства Белла: обсуждение и некоторые новые экспериментальные данные». Lettere al Nuovo Cimento. 43 (8): 345–348. Дои:10.1007 / bf02746964. S2CID 120840672.
- Д'Эспанья, Б. (1979). «Квантовая теория и реальность» (PDF). Scientific American. 241 (5): 158–181. Bibcode:1979SciAm.241e.158D. Дои:10.1038 / Scientificamerican1179-158.
- Белл, Дж. С. (1966). «К проблеме скрытых переменных в квантовой механике». Ред. Мод. Phys. 38 (3): 447–452. Bibcode:1966РвМП ... 38..447Б. Дои:10.1103 / revmodphys.38.447. OSTI 1444158.
- Белл, Дж. С. (1964). "О парадоксе Эйнштейна Подольского и Розена" (PDF). Физика Телосложение Физика. 1 (3): 195–200. Дои:10.1103 / PhysicsPhysiqueFizika.1.195.
- Дж. С. Белл, Введение в вопрос о скрытых переменных, Труды Международной школы физики «Энрико Ферми», курс IL, Основы квантовой механики (1971) 171–81
- Дж. С. Белл, Носки Бертльмана и природа реальности, Journal de Physique, Colloque C2, Suppl. au number 3, Том 42 (1981) стр. C2 41–61
- Дж. С. Белл, Разговорчивый и непроизносимый в квантовой механике (Cambridge University Press, 1987) [Сборник статей Белла, включая все вышеперечисленное.]
- Clauser, J. F .; Шимони, А. (1978). «Теорема Белла: экспериментальные проверки и следствия» (PDF). Отчеты о достижениях физики. 41 (12): 1881–1927. Bibcode:1978RPPh ... 41.1881C. CiteSeerX 10.1.1.482.4728. Дои:10.1088/0034-4885/41/12/002.
- Clauser, J. F .; Хорн, М.А. (1974). «Экспериментальные следствия объективных локальных теорий». Phys. Ред. D. 10 (2): 526–535. Bibcode:1974ПхРвД..10..526С. Дои:10.1103 / Physrevd.10.526.
- Фрай, Э. С .; Вальтер, Т .; Ли, С. (1995). «Предложение о проверке неравенств Белла без лазеек» (PDF). Phys. Ред. А. 52 (6): 4381–4395. Bibcode:1995PhRvA..52.4381F. Дои:10.1103 / Physreva.52.4381. HDL:1969.1/126533. PMID 9912775.
- Э. С. Фрай и Т. Вальтер, Тесты неравенства Белла на основе атома - наследие Джона Белла продолжается, стр 103–117 из Quantum [Un] Speechables, Р.А. Бертльманн и А. Цайлингер (ред.) (Springer, Берлин-Гейдельберг-Нью-Йорк, 2002)
- Р. Б. Гриффитс, Последовательная квантовая теория ', Издательство Кембриджского университета (2002).
- Харди, Л. (1993). «Нелокальность для 2-х частиц без неравенств почти для всех запутанных состояний». Письма с физическими проверками. 71 (11): 1665–1668. Bibcode:1993ПхРвЛ..71.1665Х. Дои:10.1103 / Physrevlett.71.1665. PMID 10054467. S2CID 11839894.
- М. А. Нильсен и И. Л. Чуанг, Квантовые вычисления и квантовая информация, Издательство Кембриджского университета (2000)
- Перл, П. (1970). «Пример скрытой переменной, основанный на отклонении данных». Физический обзор D. 2 (8): 1418–25. Bibcode:1970ПхРвД ... 2.1418П. Дои:10.1103 / Physrevd.2.1418.
- А. Перес, Квантовая теория: концепции и методы, Клувер, Дордрехт, 1993.
- П. Плух, Теория квантовой вероятности, Докторская диссертация, Клагенфуртский университет, 2006 г.
- Б. К. ван Фрассен, Квантовая механика, Кларендон Пресс, 1991.
- Rowe, M.A .; Kielpinski, D .; Meyer, V .; Sackett, C.A .; Itano, W.M .; Monroe, C .; Вайнленд, Д.Дж. (2001). «Экспериментальное нарушение неравенств Белла с эффективным обнаружением» (PDF). Природа. 409 (6822): 791–794. Bibcode:2001Натура.409..791K. Дои:10.1038/35057215. HDL:2027.42/62731. PMID 11236986. S2CID 205014115.
- Sulcs, S. (2003). «Природа света и экспериментальная физика ХХ века». Основы науки. 8 (4): 365–391. Дои:10.1023 / А: 1026323203487. S2CID 118769677.
- Gröblacher, S .; и другие. (2007). «Экспериментальная проверка нелокального реализма». Природа. 446 (7138): 871–875. arXiv:0704.2529. Bibcode:2007Натура 446..871Г. Дои:10.1038 / природа05677. PMID 17443179. S2CID 4412358.
- Мацукевич, Д. Н .; Maunz, P .; Moehring, D. L .; Olmschenk, S .; Монро, К. (2008). «Нарушение неравенства Белла с двумя удаленными атомными кубитами». Phys. Rev. Lett. 100 (15): 150404. arXiv:0801.2184. Bibcode:2008PhRvL.100o0404M. Дои:10.1103 / Physrevlett.100.150404. PMID 18518088. S2CID 11536757.
- Комикс Дилберт, к Скотт Адамс, ссылается на теорему Белла в 1992-09-21 и 1992-09-22 полоски.
- Шимони, Абнер. "Теорема Белла". В Залта, Эдуард Н. (ред.). Стэнфордская энциклопедия философии.
дальнейшее чтение
Следующие предназначены для широкой аудитории.
- Амир Д. Акзель, Запутанность: величайшая загадка физики (Четыре стены восемь окон, Нью-Йорк, 2001).
- А. Африат и Ф. Селлери, Парадокс Эйнштейна, Подольского и Розена (Plenum Press, Нью-Йорк и Лондон, 1999 г.)
- Дж. Бэгготт, Значение квантовой теории (Издательство Оксфордского университета, 1992)
- Н. Дэвид Мермин, «Есть ли луна там, когда никто не смотрит? Реальность и квантовая теория», в Физика сегодня, Апрель 1985 г., стр. 38–47.
- Луиза Гилдер, Эпоха запутанности: возрождение квантовой физики (Нью-Йорк: Альфред А. Кнопф, 2008 г.)
- Брайан Грин, Ткань космоса (Винтаж, 2004 г., ISBN 0-375-72720-5)
- Ник Герберт, Квантовая реальность: за гранью новой физики (Якорь, 1987, ISBN 0-385-23569-0)
- Д. Вик, Печально известная граница: семь десятилетий споров в квантовой физике (Биркхаузер, Бостон, 1995 г.)
- Р. Антон Уилсон, Прометей восстание (New Falcon Publications, 1997 г., ISBN 1-56184-056-4)
- Гэри Зукав "Танцующие мастера У Ли "(Многолетняя классика, 2001 г., ISBN 0-06-095968-1)
- Гольдштейн, Шелдон; и другие. (2011). "Теорема Белла". Scholarpedia. 6 (10): 8378. Bibcode:2011SchpJ ... 6.8378G. Дои:10.4249 / scholarpedia.8378.
- Мермин, Н. Д. (1981). «Возвращение домой атомного мира: квантовые загадки для всех». Американский журнал физики. 49 (10): 940–943. Bibcode:1981AmJPh..49..940M. Дои:10.1119/1.12594. S2CID 122724592.
внешняя ссылка
- Мермин: жуткие действия на расстоянии? Лекция Оппенгеймера
- Квантовая запутанность, доктор Эндрю Х. Томас.
- Теорема Белла с простыми математическими вычислениями, Дэвид Р. Шнайдер. Еще одно простое объяснение неравенства Белла.
- Интерактивные эксперименты с одиночными фотонами: запутанность и теорема Белла
- Статья Абнера Шимони о теореме Белла в Стэнфордской энциклопедии философии
- "Теорема Белла". Интернет-энциклопедия философии.
- «Колокол неравенства», Энциклопедия математики, EMS Press, 2001 [1994]
- Жуткое действие на расстоянии: объяснение теоремы Белла


































































![{ Displaystyle langle A (a) B (b) rangle Equiv langle Phi ^ {-} | left ({ frac {-1} { sqrt {2}}} S_ {z} otimes (S_ {x} + S_ {z}) right) | Phi ^ {-} rangle = - { frac {1} {2}} langle Phi ^ {-} | { Big [} | 0 rangle otimes (| 0 rangle - | 1 rangle) + | 1 rangle otimes (| 1 rangle + | 0 rangle) { Big]} = { frac {1} { sqrt { 2}}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1aadc40c17c40576f65e9e71338d8f04844e10fc)







