Фотон - Photon

Эта статья про элементарную частицу или квант света. Для использования в других целях см. Фотон (значения).

Фотон

Фотоны излучаются лазерным лучом с резьбой
Сочинение	Элементарная частица
Статистика	Бозе-Эйнштейн
Взаимодействия	Электромагнитный, Слабый, Сила тяжести
Символ	γ
Теоретически	Альберт Эйнштейн (1905) Название «фотон» обычно приписывают Гилберт Н. Льюис (1926)
Масса	0 < 1×10^−18 эВ /c^2[1]
Средняя продолжительность жизни	Стабильный[1]
Электрический заряд	0 < 1×10^−35 е[1]
Вращение	1
Паритет	−1[1]
C паритет	−1[1]
Сжатый	я (Jп C)=0,1(1^−−)[1]

В фотон это тип элементарная частица. Это квант из электромагнитное поле включая электромагнитное излучение Такие как свет и радиоволны, а носитель силы для электромагнитная сила. Фотоны безмассовый,^[а] поэтому они всегда движутся в скорость света в вакууме, 299792458 РС.

Как и все элементарные частицы, фотоны в настоящее время лучше всего объясняются квантовая механика и выставить дуальность волна-частица, в их поведении присутствуют свойства обоих волны и частицы.^[2] Современная концепция фотона зародилась в первые два десятилетия 20-го века благодаря работам Альберт Эйнштейн, которые основывались на исследованиях Макс Планк. Пытаясь объяснить, как иметь значение и электромагнитное излучение могло быть в тепловое равновесие друг с другом, Планк предположил, что энергия, запасенная в материальном объекте, должна рассматриваться как состоящая из целое число количество дискретных деталей одинакового размера. Чтобы объяснить фотоэлектрический эффект Эйнштейн представил идею о том, что свет состоит из дискретных единиц энергии. В 1926 г. Гилберт Н. Льюис популяризировал термин фотон для этих энергоблоков.^[3][4][5] Впоследствии многие другие эксперименты подтвердили подход Эйнштейна.^[6][7][8]

в Стандартная модель из физика элементарных частиц, фотоны и другие элементарные частицы описываются как необходимое следствие физических законов, имеющих определенное симметрия в каждой точке пространство-время. Внутренние свойства частиц, такие как обвинять, масса, и вращение, определяются этим калибровочная симметрия. Концепция фотона привела к значительным успехам в экспериментальной и теоретической физике, в том числе в лазеры, Конденсация Бозе – Эйнштейна, квантовая теория поля, а вероятностная интерпретация квантовой механики. Он был применен к фотохимия, микроскопия высокого разрешения, и измерения молекулярных расстояний. В последнее время фотоны изучаются как элементы квантовые компьютеры, и для приложений в оптическое изображение и оптическая связь Такие как квантовая криптография.

Номенклатура

Фотоэлектрический эффект: испускание электронов металлической пластиной, вызванное квантами света - фотонами.

1926 Гилберт Н. Льюис буква, которая ввела слово "фотон" в обиход

Слово кванты (единственное число квант Латынь для сколько ) использовался до 1900 года для обозначения частиц или количества различных количество, включая электричество. В 1900 году немецкий физик Макс Планк учился излучение черного тела, и он предположил, что экспериментальные наблюдения, в частности более короткие длины волн, можно было бы объяснить, если бы энергия, запасенная в молекуле, была «дискретной величиной, составленной из целого числа конечных равных частей», которые он назвал «элементами энергии».^[9] В 1905 г. Альберт Эйнштейн опубликовал статью, в которой предположил, что многие явления, связанные со светом, включая излучение черного тела и фотоэлектрический эффект - лучше объяснить, моделируя электромагнитные волны как состоящие из пространственно локализованных дискретных волновых пакетов.^[10] Он назвал такой волновой пакет световой квант (Немецкий: das Lichtquant).^[b]

Название фотон происходит от Греческое слово для света, φῶς (транслитерировано phôs). Артур Комптон использовал фотон в 1928 г., имея в виду Гилберт Н. Льюис, который ввел термин в письме Природа 18 декабря 1926 г.^[3][11] То же имя использовалось ранее, но никогда не было широко распространено до Льюиса: в 1916 году американским физиком и психологом Леонард Т. Троланд, в 1921 году ирландским физиком Джон Джоли, в 1924 г. французским физиологом Рене Вурмсер (1890–1993), а в 1926 году французским физиком Фритиоф Вольферс (1891–1971).^[5] Название было предложено первоначально как единица, относящаяся к освещению глаза и возникающему в результате ощущению света, а затем использовалось в физиологическом контексте. Хотя теории Вольферса и Льюиса противоречили многим экспериментам и никогда не были приняты, новое название было принято большинством физиков очень скоро после того, как Комптон использовал его.^[5][c]

В физике фотон обычно обозначают символом γ (в Греческая буква гамма ). Этот символ фотона, вероятно, происходит от гамма излучение, которые были открыты в 1900 г. Поль Вильярд,^[13][14] названный Эрнест Резерфорд в 1903 году, и было показано, что это форма электромагнитное излучение в 1914 году Резерфордом и Эдвард Андраде.^[15] В химия и оптическая инженерия, фотоны обычно обозначаются hν, какой энергия фотона, куда час является Постоянная Планка и Греческая буква ν (ню ) - фотонная частота.^[16] Гораздо реже фотон может быть обозначен как hf, где его частота обозначена ж.^[17]

Физические свойства

Фотон безмассовый,^[d] не имеет электрический заряд,^[18][19] и является стабильная частица. В вакууме фотон имеет два возможных поляризация состояния.^[20] Фотон - это калибровочный бозон за электромагнетизм,^[21]:29–30 и, следовательно, все другие квантовые числа фотона (такие как лептонное число, барионное число, и квантовые числа аромата ) равны нулю.^[22] Также фотон не подчиняется Принцип исключения Паули, но вместо этого подчиняется Статистика Бозе – Эйнштейна.^[23]:1221

Фотоны испускаются во многих природных процессах. Например, когда заряд ускоренный он излучает синхротронное излучение. Во время молекулярный, атомный или же ядерный переход к низшей уровень энергии, будут испускаться фотоны различной энергии, начиная с радиоволны к гамма излучение. Фотоны также могут испускаться, когда частица и соответствующая ей античастица находятся уничтожен (Например, электрон-позитронная аннигиляция ).^{[23]:572,1114,1172}

Релятивистская энергия и импульс

Смотрите также: Специальная теория относительности

Конус показывает возможные значения волнового 4-вектора фотона. По оси «время» отложена угловая частота (радес⁻¹ ), а ось «космос» представляет собой угловое волновое число (рад⋅м⁻¹). Зеленый и индиго представляют левую и правую поляризацию.

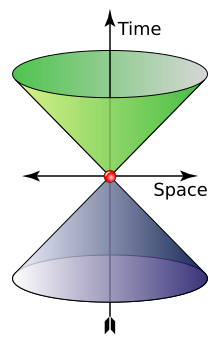
В пустом пространстве фотон движется со скоростью c (в скорость света ) и это энергия и импульс связаны E = ПК, куда п это величина вектора импульса п. Это вытекает из следующего релятивистского соотношения с м = 0:^[24]

${displaystyle E^{2}=p^{2}c^{2}+m^{2}c^{4}.}$

Энергия и импульс фотона зависят только от его частота (${displaystyle u }$) или, наоборот, его длина волны (λ):

${displaystyle E=hbar omega =hu ={frac {hc}{lambda }}}$

${displaystyle {oldsymbol {p}}=hbar {oldsymbol {k}},}$

куда k это волновой вектор (где волновое число k = |k| = 2π /λ), ω = 2πν это угловая частота, и час = час/ 2π это приведенная постоянная Планка.^[25]

С п указывает в направлении распространения фотона, величина импульса равна

${displaystyle p=hbar k={frac {hu }{c}}={frac {h}{lambda }}.}$

Фотон также несет в себе величину, называемую спиновый угловой момент это не зависит от его частоты.^[26] Поскольку фотоны всегда движутся со скоростью света, спин лучше всего выражать через компонент измеряется вдоль направления движения, его спиральность, который должен быть либо +ħ или −ħ. Эти две возможные спирали, называемые правой и левой, соответствуют двум возможным круговая поляризация состояния фотона.^[27]

Чтобы проиллюстрировать значение этих формул, аннигиляция частицы с ее античастицей в свободном пространстве должна привести к созданию по крайней мере два фотоны по следующей причине. в центр импульса кадра, сталкивающиеся античастицы не имеют чистого импульса, тогда как одиночный фотон всегда имеет импульс (поскольку, как мы видели, он определяется частотой или длиной волны фотона, которая не может быть равна нулю). Следовательно, сохранение импульса (или эквивалентно, трансляционная инвариантность ) требует создания по крайней мере двух фотонов с нулевым суммарным импульсом. (Однако возможно, если система взаимодействует с другой частицей или полем для аннигиляции, чтобы произвести один фотон, например, когда позитрон аннигилирует со связанным атомным электроном, возможно испустить только один фотон, поскольку ядерное кулоновское поле нарушает трансляционную симметрию.)^[28]:64–65 Энергия двух фотонов или, что то же самое, их частота может быть определена из сохранение четырехимпульса.

С другой стороны, фотон можно рассматривать как собственная античастица (таким образом, «антифотон» - это просто нормальный фотон). Обратный процесс, парное производство, является доминирующим механизмом, с помощью которого фотоны высоких энергий, такие как гамма излучение теряют энергию при прохождении через материю.^[29] Этот процесс противоположен «аннигиляции в один фотон», разрешенной в электрическом поле атомного ядра.

Классические формулы для энергии и импульса электромагнитное излучение можно перевыразить через фотонные события. Например, давление электромагнитного излучения на объекте происходит от передачи импульса фотона в единицу времени и единицу площади этому объекту, поскольку давление - это сила на единицу площади, а сила - это изменение импульс в единицу времени.^[30]

Каждый фотон несет две отдельные и независимые формы угловой момент света. В спиновый угловой момент света определенного фотона всегда либо +час или -час. легкий орбитальный угловой момент определенного фотона может быть любым целым числом N, в том числе ноль.^[31]

Экспериментальные проверки массы фотона

Современные общепринятые физические теории подразумевают или предполагают, что фотон строго безмассовый. Если фотон не является строго безмассовой частицей, он не будет двигаться с точной скоростью света, c, в вакууме. Его скорость будет ниже и зависит от его частоты. На относительность это не повлияет; так называемая скорость света, c, тогда была бы не фактическая скорость, с которой движется свет, а константа природы, которая является верхняя граница со скоростью, которую теоретически может достичь любой объект в пространстве-времени.^[32] Таким образом, это по-прежнему будет скорость пространственно-временной ряби (гравитационные волны и гравитоны ), но это была бы не скорость фотонов.

Если бы у фотона действительно была ненулевая масса, были бы и другие эффекты. Закон Кулона будет изменен и электромагнитное поле имел бы дополнительный физический степень свободы. Эти эффекты дают более чувствительные экспериментальные исследования массы фотона, чем частотная зависимость скорости света. Если закон Кулона не совсем верен, то это допускает наличие электрическое поле существовать внутри полого проводника, когда он подвергается воздействию внешнего электрического поля. Это обеспечивает возможность очень высокой точности тесты закона Кулона.^[33] Нулевой результат такого эксперимента установил предел м ≲ 10⁻¹⁴ эВ /c².^[34]

Более четкие верхние пределы скорости света были получены в экспериментах, направленных на обнаружение эффектов, вызванных галактическим воздействием. векторный потенциал. Хотя галактический векторный потенциал очень велик, потому что галактическое магнитное поле существует на очень больших масштабах, только магнитное поле будет наблюдаться, если фотон не имеет массы. В случае, если фотон имеет массу, массовый член 1/2м²А_μА^μ повлияет на галактическую плазму. Тот факт, что таких эффектов не наблюдается, подразумевает верхнюю границу массы фотона м < 3×10⁻²⁷ эВ /c².^[35] Галактический векторный потенциал также можно исследовать напрямую, измеряя крутящий момент, действующий на намагниченное кольцо.^[36] Такие методы использовались для получения более точного верхнего предела 1.07×10⁻²⁷ эВ /c² (эквивалент 10⁻³⁶ дальтон) данный Группа данных о частицах.^[37]

Было показано, что эти резкие пределы из-за ненаблюдения эффектов, вызванных галактическим векторным потенциалом, зависят от модели.^[38] Если масса фотона генерируется через Механизм Хиггса тогда верхний предел м ≲ 10⁻¹⁴ эВ /c² из проверки закона Кулона.

Смотрите также: Сверхновая звезда / датчик ускорения

Историческое развитие

Основная статья: Свет

Томас Янг с двухщелевой эксперимент в 1801 г. показал, что свет может действовать как волна, помогая рано обесценить частица теории света.^[23]:964

В большинстве теорий до восемнадцатого века свет изображался состоящим из частиц. С частица модели не могут легко учесть преломление, дифракция и двулучепреломление света, волновые теории света были предложены Рене Декарт (1637),^[39] Роберт Гук (1665),^[40] и Кристиан Гюйгенс (1678);^[41] однако модели частиц оставались доминирующими, в основном из-за влияния Исаак Ньютон.^[42] В начале 19 века Томас Янг и Август Френель ясно продемонстрировал вмешательство и дифракция света, и к 1850 году волновые модели стали общепринятыми.^[43] Джеймс Клерк Максвелл 1865 год прогноз^[44] этот свет был электромагнитной волной, что было экспериментально подтверждено в 1888 г. Генрих Герц обнаружение радиоволны^[45]- казалось, это последний удар по моделям частиц света.

В 1900 г. Максвелла теоретическая модель света как колеблющийся электрический и магнитные поля казалось полным. Однако некоторые наблюдения не могли быть объяснены какой-либо волновой моделью электромагнитное излучение, что привело к идее, что световая энергия была упакована в кванты описанный E = hν. Более поздние эксперименты показали, что эти световые кванты также обладают импульсом и, таким образом, могут считаться частицы: the фотон родилась концепция, ведущая к более глубокому пониманию самих электрических и магнитных полей.

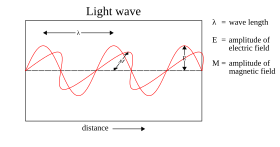
В Теория волн Максвелла, однако, не учитывает все свойства света. Теория Максвелла предсказывает, что энергия световой волны зависит только от ее интенсивность, а не на его частота; тем не менее, несколько независимых типов экспериментов показывают, что энергия, передаваемая светом атомам, зависит только от частоты света, а не от его интенсивности. Например, некоторые химические реакции провоцируются только светом с частотой выше определенного порога; свет с частотой ниже пороговой, какой бы интенсивной она ни был, не вызывает реакции. Точно так же электроны могут быть выброшены из металлической пластины, если направить на нее свет достаточно высокой частоты ( фотоэлектрический эффект ); энергия выброшенного электрона связана только с частотой света, а не с его интенсивностью.^[46][e]

В то же время исследования излучение черного тела проводились в течение четырех десятилетий (1860–1900) различными исследователями^[47] завершился Макс Планк с гипотеза^[48][49] что энергия любой система, которая поглощает или излучает электромагнитное излучение определенной частоты ν является целым кратным кванта энергии E = hν. Как показано Альберт Эйнштейн,^[10][50] некоторая форма квантования энергии должен предполагается, что учитывает тепловое равновесие, наблюдаемое между веществом и электромагнитное излучение; за это объяснение фотоэлектрического эффекта Эйнштейн получил в 1921 г. Нобелевская премия по физике.^[51]

Поскольку теория света Максвелла допускает все возможные энергии электромагнитного излучения, большинство физиков изначально предполагали, что квантование энергии является результатом какого-то неизвестного ограничения на вещество, которое поглощает или испускает излучение. В 1905 году Эйнштейн был первым, кто предположил, что квантование энергии является свойством самого электромагнитного излучения.^[10] Хотя он признал справедливость теории Максвелла, Эйнштейн указал, что многие аномальные эксперименты можно объяснить, если энергия Максвелловской световой волны были локализованы в точечные кванты, которые движутся независимо друг от друга, даже если сама волна непрерывно распространяется в пространстве.^[10] В 1909 г.^[50] и 1916 г.,^[52] Эйнштейн показал, что если Закон планка Что касается излучения черного тела, то кванты энергии также должны нести импульс п = час/λ, сделав их полноценными частицами. Этот импульс фотона экспериментально наблюдался Артур Комптон,^[53] за что он получил Нобелевскую премию в 1927 году. Главный вопрос тогда стоял: как объединить волновую теорию света Максвелла с ее экспериментально наблюдаемой частицей? Ответ на этот вопрос занимал Альберта Эйнштейна на всю оставшуюся жизнь.^[54] и был решен в квантовая электродинамика и его преемник, Стандартная модель. (Видеть § Второе квантование и § Фотон как калибровочный бозон, ниже.)

Вплоть до 1923 года большинство физиков не соглашались с квантованием самого света. Вместо этого они пытались объяснить поведение фотона квантованием только иметь значение, как в Модель Бора из атом водорода (показано здесь). Хотя эти полуклассические модели были только в первом приближении, они были точными для простых систем и привели к квантовая механика.

Предсказания Эйнштейна 1905 года были подтверждены экспериментально несколькими способами в первые два десятилетия 20-го века, как описано в Роберт Милликен Нобелевская лекция.^[55] Однако до эксперимента Комптона^[53] показали, что фотоны обладают импульсом, пропорциональным их волновое число (1922),^{[требуется полная цитата ]} большинство физиков не хотели верить, что электромагнитное излучение само по себе может быть частицами. (См., Например, Нобелевские лекции Вена,^[47] Планк^[49] и Милликен.)^[55] Вместо этого существовало широко распространенное мнение, что квантование энергии является результатом каких-то неизвестных ограничений на материю, которая поглощает или испускает излучение. Со временем отношение изменилось. Частично это изменение можно отнести к экспериментам, например, по выявлению Комптоновское рассеяние, где было гораздо сложнее не приписать квантование самому свету для объяснения наблюдаемых результатов.^[56]

Даже после эксперимента Комптона Нильс Бор, Хендрик Крамерс и Джон Слейтер сделала последнюю попытку сохранить максвелловскую модель света с непрерывным электромагнитным полем, так называемую Теория БКС.^[57] Важной особенностью теории BKS является то, как она относилась к сохранение энергии и сохранение импульса. В теории BKS энергия и импульс сохраняются в среднем только при многих взаимодействиях между веществом и излучением. Однако уточненные эксперименты Комптона показали, что законы сохранения справедливы для индивидуальных взаимодействий.^[58] Соответственно, Бор и его сотрудники устроили свою модель «похороны как можно более почетно».^[54] Тем не менее неудачи модели БКС вдохновили Вернер Гейзенберг в его развитии матричная механика.^[59]

Некоторые физики упорствовали^[60] в разработке полуклассических моделей, в которых электромагнитное излучение не квантуется, но материя, по-видимому, подчиняется законам квантовая механика. Хотя доказательства существования фотонов в результате химических и физических экспериментов к 1970-м годам были подавляющими, эти доказательства нельзя было рассматривать как абсолютно окончательный; поскольку он полагался на взаимодействие света с материей, и достаточно полная теория материи в принципе могла бы объяснить доказательства. Тем не менее, все полуклассические теории были окончательно опровергнуты в 1970-х и 1980-х годах экспериментами по фотонной корреляции.^[f] Следовательно, гипотеза Эйнштейна о том, что квантование - это свойство самого света, считается доказанной.

Принципы двойственности волны и частицы и неопределенности

Фотоны в Интерферометр Маха – Цендера проявлять волновую интерференцию и детектирование частиц на однофотонные детекторы.

Фотоны подчиняются законам квантовой механики, поэтому их поведение имеет как волновые, так и частичные аспекты. Когда фотон обнаруживается измерительным прибором, он регистрируется как единое целое, состоящее из частиц. Тем не менее вероятность обнаружения фотона рассчитывается по уравнениям, описывающим волны. Эта комбинация аспектов известна как дуальность волна-частица. Например, распределение вероятностей для места, в котором может быть обнаружен фотон, явно проявляются волновые явления, такие как дифракция и вмешательство. Одиночный фотон, проходящий через двухщелевой эксперимент приземляется на экран с распределением вероятностей, заданным его интерференционной картиной, определяемой Уравнения Максвелла.^[61] Однако эксперименты подтверждают, что фотон нет короткий импульс электромагнитного излучения; он не распространяется, когда он распространяется, и он не делится, когда сталкивается с Разделитель луча.^[62] Скорее фотон кажется точечная частица поскольку он поглощается или выделяется в целом сколь угодно малыми системами, в том числе системами, намного меньшими длины его волны, такими как атомное ядро ​​(≈10⁻¹⁵ м) или даже точечный электрон.

Хотя во многих вводных текстах фотоны рассматриваются с использованием математических методов нерелятивистской квантовой механики, это в некотором смысле является неудобным упрощением, поскольку фотоны по своей природе являются релятивистскими по своей природе. Поскольку фотоны имеют ноль масса покоя, нет волновая функция определенный для фотона может иметь все свойства, знакомые по волновым функциям нерелятивистской квантовой механики.^[грамм] Чтобы избежать этих трудностей, физики используют вторично квантованную теорию фотонов, описанную ниже: квантовая электродинамика, в котором фотоны представляют собой квантованные возбуждения электромагнитных мод.^[67]

Еще одна трудность - найти подходящий аналог для принцип неопределенности, идея, которую часто приписывают Гейзенбергу, который ввел эту концепцию в анализ мысленный эксперимент с участием электрон и фотон высокой энергии. Однако Гейзенберг не дал точных математических определений того, что означает «неопределенность» в этих измерениях. Точная математическая формулировка принципа неопределенности положения-импульса обусловлена Кеннард, Паули, и Weyl.^[68][69] Принцип неопределенности применяется к ситуациям, когда экспериментатор может выбрать измерение одной из двух «канонически сопряженных» величин, таких как положение и импульс частицы. Согласно принципу неопределенности, независимо от того, как частица подготовлена, невозможно сделать точный прогноз для обоих из двух альтернативных измерений: если результат измерения положения становится более определенным, результат измерения импульса становится меньше, и наоборот.^[70] А когерентное состояние сводит к минимуму общую неопределенность, насколько позволяет квантовая механика.^[67] Квантовая оптика использует когерентные состояния для мод электромагнитного поля. Существует компромисс, напоминающий соотношение неопределенности положения и количества движения, между измерениями амплитуды и фазы электромагнитной волны.^[67] Иногда это неофициально выражается в терминах неопределенности количества фотонов, присутствующих в электромагнитной волне, ${displaystyle Delta N}$, а неопределенность фазы волны ${displaystyle Delta phi }$. Однако это не может быть соотношением неопределенностей типа Кеннарда – Паули – Вейля, поскольку в отличие от положения и импульса фазовая ${displaystyle phi }$ не может быть представлен Эрмитов оператор.^[71]

Модель Бозе – Эйнштейна фотонного газа.

Основные статьи: Бозе-газ, Статистика Бозе – Эйнштейна, Теорема спиновой статистики, Газ в коробке, и Фотонный газ

В 1924 г. Сатьендра Нат Бос полученный Закон планка о излучении черного тела без использования какого-либо электромагнетизма, а, скорее, с использованием модификации крупнозернистого подсчета фазовое пространство.^[72] Эйнштейн показал, что эта модификация эквивалентна предположению, что фотоны строго идентичны, и что это подразумевает «загадочное нелокальное взаимодействие»,^[73][74] теперь понимается как требование симметричное квантово-механическое состояние. Эта работа привела к концепции когерентные состояния и развитие лазера. В тех же статьях Эйнштейн распространил формализм Бозе на материальные частицы (бозоны ) и предсказал, что они сконденсируются до самого низкого квантовое состояние при достаточно низких температурах; это Конденсация Бозе – Эйнштейна наблюдалась экспериментально в 1995 г.^[75] Позже он был использован Лене Хау замедлить, а затем полностью остановиться, загореться в 1999 г.^[76] и 2001.^[77]

Современный взгляд на это состоит в том, что фотоны в силу их целочисленного спина бозоны (в отличие от фермионы с полуцелым спином). Посредством теорема спиновой статистики, все бозоны подчиняются статистике Бозе – Эйнштейна (тогда как все фермионы подчиняются Статистика Ферми – Дирака ).^[78]

Вынужденное и спонтанное излучение

Основные статьи: Вынужденное излучение и Лазер

Вынужденное излучение (в котором фотоны «клонируют» себя) было предсказано Эйнштейном в его кинетическом анализе и привело к развитию лазер. Вывод Эйнштейна вдохновил дальнейшее развитие квантовой трактовки света, что привело к статистической интерпретации квантовой механики.

В 1916 году Альберт Эйнштейн показал, что закон излучения Планка может быть выведен из полуклассической статистической обработки фотонов и атомов, которая подразумевает связь между скоростью, с которой атомы испускают и поглощают фотоны. Условие следует из предположения, что функции испускания и поглощения излучения атомами независимы друг от друга и что тепловое равновесие достигается за счет взаимодействия излучения с атомами. Рассмотрим полость в тепловое равновесие со всеми частями себя и наполненными электромагнитное излучение и что атомы могут испускать и поглощать это излучение. Тепловое равновесие требует, чтобы плотность энергии ${displaystyle ho (u )}$ фотонов с частотой ${displaystyle u }$ (что пропорционально их числовая плотность ) в среднем постоянна во времени; следовательно, скорость, с которой фотоны любой конкретной частоты испускается должны равняться скорости, с которой они поглощен.^[79]

Эйнштейн начал с постулирования простых соотношений пропорциональности для различных скоростей реакции. В его модели ставка ${displaystyle R_{ji}}$ для системы впитывать фотон частоты ${displaystyle u }$ и переход от более низкой энергии ${displaystyle E_{j}}$ к более высокой энергии ${displaystyle E_{i}}$ пропорционально числу ${displaystyle N_{j}}$ атомов с энергией ${displaystyle E_{j}}$ и к плотности энергии ${displaystyle ho (u )}$ окружающих фотонов этой частоты,

${displaystyle R_{ji}=N_{j}B_{ji}ho (u )!}$

куда ${displaystyle B_{ji}}$ это константа скорости для впитывания. Для обратного процесса есть две возможности: спонтанное испускание фотона или испускание фотона, инициированное взаимодействием атома с проходящим фотоном, и возвращение атома в состояние с более низкой энергией. Следуя подходу Эйнштейна, соответствующая скорость ${displaystyle R_{ij}}$ для излучения фотонов с частотой ${displaystyle u }$ и переход от более высокой энергии ${displaystyle E_{i}}$ к более низкой энергии ${displaystyle E_{j}}$ является

${displaystyle R_{ij}=N_{i}A_{ij}+N_{i}B_{ij}ho (u )!}$

куда ${displaystyle A_{ij}}$ - константа скорости для испускать фотон спонтанно, и ${displaystyle B_{ij}}$ - константа скорости излучения в ответ на фотоны окружающей среды (индуцированное или стимулированное излучение ). В термодинамическом равновесии количество атомов в состоянии ${displaystyle i}$ и те, кто в состоянии ${displaystyle j}$ в среднем должно быть постоянным; следовательно, ставки ${displaystyle R_{ji}}$ и ${displaystyle R_{ij}}$ должны быть равны. Кроме того, по рассуждениям, аналогичным выводам Статистика Больцмана, соотношение ${displaystyle N_{i}}$ и ${displaystyle N_{j}}$ является ${displaystyle g_{i}/g_{j}exp {(E_{j}-E_{i})/(kT)},}$ куда ${displaystyle g_{i}}$ и ${displaystyle g_{j}}$ являются вырождение государства ${displaystyle i}$ и что из ${displaystyle j}$, соответственно, ${displaystyle E_{i}}$ и ${displaystyle E_{j}}$ их энергия, ${displaystyle k}$ то Постоянная Больцмана и ${displaystyle T}$ система температура. Отсюда легко выводится, что${displaystyle g_{i}B_{ij}=g_{j}B_{ji}}$ и

${displaystyle A_{ij}={frac {8pi hu ^{3}}{c^{3}}}B_{ij}.}$

В ${displaystyle A_{ij}}$ и ${displaystyle B_{ij}}$ все вместе известны как Коэффициенты Эйнштейна.^[80]

Эйнштейн не мог полностью обосновать свои уравнения скорости, но утверждал, что должна быть возможность вычислить коэффициенты ${displaystyle A_{ij}}$, ${displaystyle B_{ji}}$ и ${displaystyle B_{ij}}$ когда-то физики получили «механику и электродинамику, модифицированные с учетом квантовой гипотезы».^[81] Вскоре после этого, в 1926 году, Поль Дирак получил ${displaystyle B_{ij}}$ константы скорости с использованием полуклассического подхода,^[82] и в 1927 г. удалось вывести все константы скорости из первых принципов в рамках квантовой теории.^[83][84] Работа Дирака была основой квантовой электродинамики, то есть квантования самого электромагнитного поля. Подход Дирака также называют второе квантование или же квантовая теория поля;^[85][86][87] более ранние методы квантовой механики рассматривали только материальные частицы как квантовомеханические, а не электромагнитное поле.

Эйнштейна беспокоил тот факт, что его теория казалась неполной, поскольку она не определяла направление спонтанно испускаемого фотона. Вероятностный характер движения легких частиц впервые был рассмотрен Ньютон в его обращении с двулучепреломление и, в более общем смысле, разделение световых лучей на границах раздела на переданный луч и отраженный луч. Ньютон предположил, что скрытые переменные в легкой частице определяют, какой из двух путей пойдет одиночный фотон.^[42] Точно так же Эйнштейн надеялся на более полную теорию, которая не оставляла бы ничего на волю случая, начиная свое разделение.^[54] из квантовой механики. Как ни странно, Макс Борн с вероятностная интерпретация из волновая функция^[88][89] был вдохновлен более поздней работой Эйнштейна в поисках более полной теории.^[90]

Квантовая теория поля

Квантование электромагнитного поля

Основная статья: Квантовая теория поля

Разные электромагнитные режимы (например, изображенные здесь) можно рассматривать как независимые простые гармонические осцилляторы. Фотон соответствует единице энергии E = hν в электромагнитном режиме.

В 1910 г. Питер Дебай полученный Закон планка о излучении черного тела из относительно простого предположения.^[91] Он разложил электромагнитное поле в полости на его Моды Фурье, и предположил, что энергия в любом режиме была целым числом, кратным ${displaystyle hu }$, куда ${displaystyle u }$ - частота электромагнитного режима. Закон Планка о излучении черного тела немедленно следует в виде геометрической суммы. Однако подход Дебая не смог дать правильную формулу для флуктуаций энергии излучения черного тела, которую Эйнштейн вывел в 1909 году.^[50]

В 1925 г. Родившийся, Гейзенберг и Иордания ключевую интерпретацию концепции Дебая.^[92] Как можно классически показать, Моды Фурье из электромагнитное поле - полный набор электромагнитных плоских волн, индексированных их волновым вектором k и состояние поляризации - эквивалентны набору несвязанных простые гармонические осцилляторы. Известно, что с квантовой механикой уровни энергии таких осцилляторов ${displaystyle E=nhu }$, куда ${displaystyle u }$ - частота генератора. Ключевым новым шагом было определение электромагнитной моды с энергетической ${displaystyle E=nhu }$ как государство с ${displaystyle n}$ фотоны, каждый из энергии ${displaystyle hu }$. Такой подход дает правильную формулу флуктуации энергии.

Диаграмма Фейнмана двух электронов, взаимодействующих путем обмена виртуальным фотоном.

Дирак сделал еще один шаг вперед.^[83][84] Он рассматривал взаимодействие между зарядом и электромагнитным полем как небольшое возмущение, которое вызывает переходы в состояниях фотонов, изменяя количество фотонов в модах, сохраняя при этом энергию и импульс в целом. Дирак смог вывести Эйнштейновскую ${displaystyle A_{ij}}$ и ${displaystyle B_{ij}}$ коэффициенты из первых принципов и показали, что статистика фотонов Бозе-Эйнштейна является естественным следствием правильного квантования электромагнитного поля (рассуждения Бозе пошли в противоположном направлении; он вывел Закон планка о излучении черного тела к предполагая B – E статистика). Во времена Дирака еще не было известно, что все бозоны, включая фотоны, должны подчиняться статистике Бозе – Эйнштейна.

Второй порядок Дирака теория возмущений может включать виртуальные фотоны, переходные промежуточные состояния электромагнитного поля; статика электрический и магнитный взаимодействия опосредуются такими виртуальными фотонами. В таком квантовые теории поля, то амплитуда вероятности наблюдаемых событий рассчитывается путем суммирования все возможные промежуточные шаги, даже нефизические; следовательно, виртуальные фотоны не обязаны удовлетворять ${displaystyle E=pc}$, и может иметь дополнительные поляризация состояния; в зависимости от измерять Используемые виртуальные фотоны могут иметь три или четыре состояния поляризации вместо двух состояний реальных фотонов. Хотя эти временные виртуальные фотоны невозможно наблюдать, они вносят ощутимый вклад в вероятность наблюдаемых событий. Действительно, такие вычисления возмущений второго и более высоких порядков, по-видимому, могут дать бесконечный взносы на сумму. Такие нефизические результаты исправлены за счет использования техники перенормировка.^[93]

Другие виртуальные частицы также могут вносить вклад в суммирование; например, два фотона могут косвенно взаимодействовать через виртуальные электрон –позитрон пары.^[94] Такое фотон-фотонное рассеяние (см. двухфотонная физика ), а также электрон-фотонное рассеяние, должно быть одним из режимов работы планируемого ускорителя частиц, Международный линейный коллайдер.^[95]

В современная физика обозначение, квантовое состояние электромагнитного поля записывается как Состояние Фока, а тензорное произведение состояний для каждого электромагнитного режима

${displaystyle |n_{k_{0}}angle otimes |n_{k_{1}}angle otimes dots otimes |n_{k_{n}}angle dots }$

куда ${displaystyle |n_{k_{i}}angle }$ представляет состояние, в котором ${displaystyle ,n_{k_{i}}}$ фотоны находятся в режиме ${displaystyle k_{i}}$. В этих обозначениях создание нового фотона в режиме ${displaystyle k_{i}}$ (например, испущенный атомным переходом) записывается как ${displaystyle |n_{k_{i}}angle ightarrow |n_{k_{i}}+1angle }$. Эти обозначения просто выражают концепцию Борна, Гейзенберга и Джордана, описанную выше, и не добавляют никакой физики.

Как калибровочный бозон

Основная статья: Калибровочная теория

Электромагнитное поле можно понимать как калибровочное поле, т.е. как поле, которое возникает из требования, чтобы калибровочная симметрия выполнялась независимо в каждой позиции в пространство-время.^[96] Для электромагнитное поле, эта калибровочная симметрия является Абелев U (1) симметрия из сложные числа абсолютного значения 1, что отражает возможность варьировать фаза сложного поля, не затрагивая наблюдаемые или же действительные функции сделаны из него, например энергия или Лагранжиан.

Кванты Абелево калибровочное поле должны быть безмассовые, незаряженные бозоны, пока не нарушена симметрия; следовательно, предсказано, что фотон будет безмассовым и иметь нулевое электрический заряд и целочисленное вращение. Особая форма электромагнитное взаимодействие указывает, что фотон должен иметь вращение ± 1; таким образом, его спиральность должно быть ${displaystyle pm hbar }$. Эти две спиновые компоненты соответствуют классическим представлениям о правая и левая круговая поляризация свет. Однако временный виртуальные фотоны из квантовая электродинамика может также принимать нефизические состояния поляризации.^[96]

В преобладающем Стандартная модель физики фотон - один из четырех калибровочные бозоны в электрослабое взаимодействие; то другие три обозначаются W⁺, Вт⁻ и Z⁰ и несут ответственность за слабое взаимодействие. В отличие от фотона, эти калибровочные бозоны имеют масса, благодаря механизм что ломает их SU (2) калибровочная симметрия. Объединение фотона с калибровочными бозонами W и Z в электрослабом взаимодействии осуществлено Шелдон Глэшоу, Абдус Салам и Стивен Вайнберг, за что были награждены премией 1979 г. Нобелевская премия по физике.^[97][98][99] Физики продолжают выдвигать гипотезы теории великого объединения которые соединяют эти четыре калибровочные бозоны с восьмеркой глюон калибровочные бозоны квантовая хромодинамика; однако ключевые предсказания этих теорий, такие как распад протона, экспериментально не наблюдались.^[100]

Адронные свойства

Основная статья: Структурная функция фотона

Измерения взаимодействия энергичных фотонов и адроны показывают, что взаимодействие гораздо более интенсивное, чем ожидалось при взаимодействии простых фотонов с электрическим зарядом адрона. Кроме того, взаимодействие энергичных фотонов с протонами аналогично взаимодействию фотонов с нейтронами.^[101] несмотря на то, что структура электрического заряда протонов и нейтронов существенно различается. Теория под названием Доминирование векторной мезоны (VMD) был разработан, чтобы объяснить этот эффект. Согласно VMD, фотон представляет собой суперпозицию чистого электромагнитного фотона, который взаимодействует только с электрическими зарядами и векторными мезонами.^[102] Однако, если экспериментально исследовать на очень коротких расстояниях, внутренняя структура фотона распознается как поток кварковых и глюонных компонентов, квазисвободных согласно асимптотической свободе в QCD и описан структурная функция фотона.^[103][104] Подробное сравнение данных с теоретическими предсказаниями было представлено в обзоре 2000 г.^[105]

Вклад в массу системы

Смотрите также: Масса в специальной теории относительности и Масса в общей теории относительности

Энергия системы, излучающей фотон, равна уменьшился по энергии ${displaystyle E}$ фотона, измеренного в системе покоя излучающей системы, что может привести к уменьшению массы в количестве ${displaystyle {E}/{c^{2}}}$. Точно так же масса системы, поглощающей фотон, равна повысился на соответствующую сумму. В качестве приложения энергетический баланс ядерных реакций с участием фотонов обычно записывается в терминах масс участвующих ядер и в терминах формы ${displaystyle {E}/{c^{2}}}$ для гамма-фотонов (и для других соответствующих энергий, таких как энергия отдачи ядер).^[106]

Эта концепция применяется в ключевых прогнозах квантовая электродинамика (QED, см. Выше). В этой теории масса электронов (или, в более общем смысле, лептонов) модифицируется путем включения массовых вкладов виртуальных фотонов в методику, известную как перенормировка. Такой "радиационные поправки "внести свой вклад в ряд предсказаний QED, таких как магнитный дипольный момент из лептоны, то Баранина сдвиг, а сверхтонкая структура связанных лептонных пар, таких как мюоний и позитроний.^[107]

Поскольку фотоны вносят вклад в тензор энергии-импульса, они оказывают гравитационное притяжение на других объектах, согласно теории общая теория относительности. И наоборот, на фотоны действует гравитация; их обычно прямые траектории могут быть искривлены пространство-время, как в гравитационное линзирование, и их частоты могут быть понижены перейдя на более высокую гравитационный потенциал, как в Эксперимент Паунда – Ребки. Однако эти эффекты не специфичны для фотонов; точно такие же эффекты были бы предсказаны для классических электромагнитные волны.^[108]

В вопросе

Смотрите также: Групповая скорость и Фотохимия

Свет, проходящий сквозь прозрачную материю, движется с меньшей скоростью, чем c, скорость света в вакууме. Фактор, на который уменьшается скорость, называется показатель преломления материала. В классической волновой картине замедление можно объяснить светом электрическая поляризация в этом случае поляризованная материя излучает новый свет, и этот новый свет мешает исходной световой волне, образуя задержанную волну. В картине частицы замедление можно вместо этого описать как смешение фотона с квантовыми возбуждениями материи, чтобы произвести квазичастицы известный как поляритон (видеть этот список для некоторых других квазичастиц); этот поляритон имеет ненулевой эффективная масса, что означает, что он не может путешествовать на c. Свет разных частот может проходить через материю на разные скорости; это называется разброс (не путать с рассеянием). В некоторых случаях это может привести к чрезвычайно низкие скорости света в зависимости. Эффекты взаимодействия фотонов с другими квазичастицами можно наблюдать непосредственно в Рамановское рассеяние и Рассеяние Бриллюэна.^[109]

Фотоны могут рассеиваться веществом. Например, фотоны совершают так много столкновений на пути от ядро Солнца что лучистой энергии может потребоваться около миллиона лет, чтобы достичь поверхности;^[110] однако, оказавшись в открытом космосе, фотон достигает Земли всего за 8,3 минуты.^[111]

Фотоны также могут быть поглощен ядрами, атомами или молекулами, вызывая переходы между их уровни энергии. Классический пример - молекулярный переход сетчатка (C₂₀ЧАС₂₈O), который отвечает за зрение, как обнаружил в 1958 году нобелевский лауреат биохимик Джордж Уолд и коллеги. Поглощение вызывает цис – транс изомеризация это, в сочетании с другими подобными переходами, преобразуется в нервные импульсы. Поглощение фотонов может даже разрушить химические связи, как в фотодиссоциация из хлор; это предмет фотохимия.^[112][113]

Технологические приложения

Фотоны находят множество применений в технике. Эти примеры выбраны для иллюстрации применения фотонов. как таковой, а не обычные оптические устройства, такие как линзы и т. д., которые могли бы работать согласно классической теории света. Лазер - чрезвычайно важная область применения, о которой говорилось выше в разделе стимулированное излучение.

Отдельные фотоны можно обнаружить несколькими способами. Классический фотоумножитель трубка эксплуатирует фотоэлектрический эффект: фотон с достаточной энергией ударяется о металлическую пластину и выбивает электрон, инициируя постоянно усиливающуюся лавину электронов. Полупроводник устройство с зарядовой связью чипы используют похожий эффект: падающий фотон генерирует заряд на микроскопическом конденсатор что можно обнаружить. Другие детекторы, такие как Счетчики Гейгера использовать способность фотонов ионизировать молекулы газа, содержащиеся в устройстве, вызывающие заметное изменение проводимость газа.^[114]

Формула энергии Планка ${displaystyle E=hu }$ часто используется инженерами и химиками при проектировании, как для вычисления изменения энергии в результате поглощения фотона, так и для определения частоты света, излучаемого при данном излучении фотона. Например, спектр излучения из газоразрядная лампа может быть изменен путем заполнения его (смесями) газов с различными электронными уровень энергии конфигурации.^[115]

При некоторых условиях энергетический переход может быть возбужден «двумя» фотонами, что по отдельности было бы недостаточно. Это позволяет использовать микроскопию с более высоким разрешением, поскольку образец поглощает энергию только в спектре, в котором два луча разного цвета значительно перекрываются, что может быть намного меньше, чем объем возбуждения одного луча (см. микроскопия с двухфотонным возбуждением ). Более того, эти фотоны меньше повреждают образец, так как имеют меньшую энергию.^[116]

В некоторых случаях два энергетических перехода могут быть связаны так, что когда одна система поглощает фотон, другая соседняя система «крадет» его энергию и повторно излучает фотон с другой частотой. Это основа флуоресцентный резонансный перенос энергии, техника, которая используется в молекулярная биология изучить взаимодействие подходящих белки.^[117]

Несколько разных видов аппаратные генераторы случайных чисел включают обнаружение одиночных фотонов. В одном примере для каждого бита в случайной последовательности, которая должна быть произведена, фотон отправляется в Разделитель луча. В такой ситуации возможны два равновероятных исхода. Фактический результат используется для определения того, является ли следующий бит в последовательности «0» или «1».^[118][119]

Квантовая оптика и вычисления

Много исследований было посвящено применению фотонов в области квантовая оптика. Фотоны кажутся хорошо подходящими в качестве элементов чрезвычайно быстрого квантовый компьютер, а квантовая запутанность фотонов является центром исследований. Нелинейно-оптические процессы - еще одна активная область исследований с такими темами, как двухфотонное поглощение, фазовая самомодуляция, модуляционная неустойчивость и оптические параметрические генераторы. Однако такие процессы обычно не требуют предположения о фотонах как таковой; их часто можно смоделировать, рассматривая атомы как нелинейные осцилляторы. Нелинейный процесс спонтанное параметрическое преобразование с понижением частоты часто используется для создания однофотонных состояний. Наконец, фотоны важны в некоторых аспектах оптическая связь, особенно для квантовая криптография.^[час]

Двухфотонная физика изучает взаимодействия между фотонами, которые встречаются редко. В 2018 году исследователи Массачусетского технологического института объявили об открытии связанных триплетов фотонов, которые могут включать поляритоны.^[120][121]

Смотрите также

• Физический портал

• Расширенный источник фотонов в Аргоннской национальной лаборатории
• Баллистический фотон
• Уравнение Дирака
• Эффект Допплера
• Парадокс ЭПР
• Технология получения рентгеновских изображений высокой энергии
• Светоносный эфир
• Медипикс
• Фонон
• Фотография
• Подсчет фотонов
• Энергия фотона
• Фотонная эпоха
• Поляризация фотона
• Фотонная молекула
• Фотоника
• Однофотонный источник
• Спиновый угловой момент света
• Статические силы и обмен виртуальными частицами

Примечания

1. Фотон инвариантная масса (также называемая «массой покоя» для массивных частиц) считается равной нулю. Это понятие массы частицы обычно используется современными физиками. У фотона действительно ненулевой релятивистская масса, в зависимости от его энергии, но это зависит от точка зрения.
2. Хотя 1967 Elsevier перевод нобелевской лекции Планка интерпретирует Lichtquant как «фотон», более буквальный перевод 1922 года Ганса Тахера Кларка и Людвика Зильберштейна Планк, Макс (1922). Зарождение и развитие квантовой теории. Кларендон Пресс. (здесь ) использует «квант света». Нет никаких доказательств того, что сам Планк использовал термин «фотон» к 1926 г. (смотрите также ).
3. Айзек Азимов кредиты Артур Комптон с определением квантов энергии как фотонов в 1923 году.^[12]
4. В масса фотона считается равным нулю. Некоторые источники также ссылаются на релятивистская масса, которая представляет собой просто энергию, приведенную к единицам массы. Для фотона с длиной волны λ или энергия E, это час/λc или же E/c². Такое использование термина «масса» больше не используется в научной литературе. Дополнительная информация: Какая масса у фотона?
5. Фраза «независимо от того, насколько интенсивна» относится к интенсивности ниже примерно 10¹³ Вт / см² в какой момент теория возмущений начинает ломаться. Напротив, в интенсивном режиме, который для видимого света превышает примерно 10¹⁴ Вт / см²классическое волновое описание правильно предсказывает энергию, приобретаемую электронами, называемую пондеромоторная энергия. (Смотрите также: Boreham, Брюс У .; Гора, Генрих; Болтон, Пол Р. (1996). «Плотность фотонов и принцип соответствия электромагнитного взаимодействия». Материалы конференции AIP. 369: 1234–1243. Bibcode:1996AIPC..369.1234B. Дои:10.1063/1.50410.) Для сравнения, солнечный свет составляет всего около 0,1 Вт / см.².
6. Эти эксперименты дают результаты, которые нельзя объяснить ни одной классической теорией света, поскольку они включают антикорреляции, возникающие в результате квантовый процесс измерения. В 1974 году первый такой эксперимент был проведен Клаузером, который сообщил о нарушении классического Неравенство Коши – Шварца. В 1977 году Кимбл и другие. продемонстрировал аналогичный эффект антигруппировки фотонов, взаимодействующих с светоделителем; этот подход был упрощен, а источники ошибок устранены в эксперименте Гранжье по фотонной антикорреляции. и другие. (1986). Эта работа рассмотрена и упрощена в Thorn. и другие. (2004). (Эти ссылки перечислено ниже.)
7. Проблема была впервые сформулирована Теодором Дадделлом Ньютоном и Юджин Вигнер.^[63][64][65] Проблемы возникают из-за фундаментального характера Группа Лоренца, который описывает симметрии пространство-время в специальной теории относительности. В отличие от генераторов Галилеевы преобразования, генераторы Лоренц усиливает не коммутируют, и поэтому одновременное присвоение низкой неопределенности всем координатам положения релятивистской частицы становится проблематичным.^[66]
8. Материалы вводного уровня по различным разделам квантовой оптики можно найти в Фокс, М. (2006). Квантовая оптика: введение. Издательство Оксфордского университета. ISBN  978-0-19-856673-1.

Рекомендации

1. Amsler, C .; и другие. (Группа данных о частицах ) (2008). «Обзор физики элементарных частиц: калибровочные бозоны и бозоны Хиггса» (PDF). Письма по физике B. 667 (1): 1. Bibcode:2008ФЛБ..667 .... 1А. Дои:10.1016 / j.physletb.2008.07.018.
2. Джус, Джордж (1951). Теоретическая физика. Лондон и Глазго: Blackie and Son Limited. п. 679.
3. «18 декабря 1926 года: Гилберт Льюис монтирует« фотон »в письме к природе». www.aps.org. Получено 2019-03-09.
4. "Гилберт Н. Льюис". Фонд атомного наследия. Получено 2019-03-09.
5. Краг, Хельге (2014). «Фотон: Новый свет на старое имя». arXiv:1401.0293 [Physics.hist-ph ].
6. Комптон, Артур Х. (1965) [12 декабря 1927]. «Рентгеновские лучи как раздел оптики» (PDF). Из Нобелевских лекций по физике 1922–1941 гг.. Амстердам: Издательство Elsevier.
7. Kimble, H.J .; Dagenais, M .; Мандель, Л. (1977). «Антигруппирование фотонов в резонансной флуоресценции» (PDF). Письма с физическими проверками. 39 (11): 691–695. Bibcode:1977ПхРвЛ..39..691К. Дои:10.1103 / PhysRevLett.39.691.
8. Grangier, P .; Roger, G .; Аспект, А. (1986). «Экспериментальные доказательства эффекта антикорреляции фотонов на светоделителе: новый свет на однофотонные помехи». Письма еврофизики. 1 (4): 173–179. Bibcode:1986EL ...... 1..173G. CiteSeerX  10.1.1.178.4356. Дои:10.1209/0295-5075/1/4/004.
9. Краг, Хельге (2000-12-01). «Макс Планк: упорный революционер». Мир физики. 13 (12): 31. Дои:10.1088/2058-7058/13/12/34.
10. Эйнштейн, А. (1905). "Über einen die Erzeugung und Verwandlung des Lichtes betreffenden heuristischen Gesichtspunkt" (PDF). Annalen der Physik (на немецком). 17 (6): 132–148. Bibcode:1905AnP ... 322..132E. Дои:10.1002 / andp.19053220607.. An английский перевод доступен из Wikisource.
11. «Разногласия между опытом и электромагнитной теорией района». В книге «Электроны и фотоны». Rapports et Discussions de Cinquième Conseil de Physique, под редакцией Institut International de Physique Solvay. Париж: Готье-Виллар, стр. 55–85.
12. Азимов Исаак (1983). Нейтрино: призрачная частица атома. Гарден-Сити, Нью-Йорк: Avon Books. ISBN  978-0-380-00483-6. и Азимов Исаак (1971). Вселенная: от плоской земли до квазара. Нью-Йорк: Уокер. ISBN  978-0-8027-0316-3. LCCN  66022515.
13. Виллар, П. (1900). "Sur la réflexion et la refraction des rayons cathodiques et des Rayons déviables du radium". Comptes Rendus des Séances de l'Académie des Sciences (На французском). 130: 1010–1012.
14. Виллар, П. (1900). "Sur le rayonnement du radium". Comptes Rendus des Séances de l'Académie des Sciences (На французском). 130: 1178–1179.
15. Резерфорд, Э.; Андраде, E.N.C. (1914). "Длина волны мягкого гамма-излучения радия B". Философский журнал. 27 (161): 854–868. Дои:10.1080/14786440508635156.
16. Эндрю Лиддл (2015). Введение в современную космологию. Джон Вили и сыновья. п. 16. ISBN  978-1-118-69025-3.
17. СантоПьетро, ​​Давид. «Энергия фотонов». Ханская академия. Получено 2020-03-15.
18. Фриш, Дэвид Х.; Торндайк, Алан М. (1964). Элементарные частицы. Принстон, штат Нью-Джерси: Дэвид Ван Ностранд. п. 22.
19. Кобычев, В.В .; Попов, С. (2005). «Ограничения на заряд фотона из наблюдений внегалактических источников». Письма об астрономии. 31 (3): 147–151. arXiv:hep-ph / 0411398. Bibcode:2005AstL ... 31..147K. Дои:10.1134/1.1883345.
20. Мэтью Д. Шварц (2014). Квантовая теория поля и стандартная модель. Издательство Кембриджского университета. п. 66. ISBN  978-1-107-03473-0.
21. Роль калибровочного бозона и поляризационный раздел 5.1 в Aitchison, I.J.R .; Привет, A.J.G. (1993). Калибровочные теории в физике элементарных частиц. IOP Publishing. ISBN  978-0-85274-328-7.
22. См. Стр.31 в Amsler, C .; и другие. (2008). «Обзор физики элементарных частиц» (PDF). Письма по физике B. 667 (1–5): 1–1340. Bibcode:2008ФЛБ..667 .... 1А. Дои:10.1016 / j.physletb.2008.07.018. PMID  10020536.
23. Холлидей, Дэвид; Резник, Роберт; Уокер, Джерл (2005), Основы физики (7-е изд.), John Wiley and Sons, Inc., ISBN  978-0-471-23231-5
24. См. Раздел 1.6 в Алонсо и Финн 1968, Раздел 1.6
25. Дэвисон Э. Сопер, Электромагнитное излучение состоит из фотонов, Институт теоретических наук, Орегонский университет
26. Это свойство было экспериментально подтверждено Раманом и Бхагавантамом в 1931 году: Раман, К.В.; Бхагавантам, С. (1931). «Экспериментальное доказательство вращения фотона» (PDF). Индийский журнал физики. 6 (3244): 353. Bibcode:1932Натура.129 ... 22R. Дои:10.1038 / 129022a0. HDL:10821/664. Архивировано из оригинал (PDF) на 2016-06-03. Получено 2008-12-28.
27. Берджесс, С .; Мур, Г. (2007). "1.3.3.2". Стандартная модель. Праймер. Издательство Кембриджского университета. ISBN  978-0-521-86036-9.
28. Гриффитс, Дэвид Дж. (2008), Введение в элементарные частицы (2-е изд. Перераб.), ВИЛИ-ВЧ, ISBN  978-3-527-40601-2
29. Алонсо и Финн 1968, Раздел 9.3
30. Например, Приложение XXXII в Родился, Макс; Блин-Стойл, Роджер Джон; Рэдклифф, Дж. М. (1989). Атомная физика. Курьерская корпорация. ISBN  978-0-486-65984-8.
31. Алан Э. Уиллнер.«Искривленный свет может значительно повысить скорость передачи данных: орбитальный угловой момент может поднять оптическую и радиосвязь на новый уровень».2016.
32. Мермин, Дэвид (февраль 1984). «Относительность без света». Американский журнал физики. 52 (2): 119–124. Bibcode:1984AmJPh..52..119M. Дои:10.1119/1.13917.
33. Plimpton, S .; Лоутон, В. (1936). «Очень точный тест закона силы Кулона между зарядами». Физический обзор. 50 (11): 1066. Bibcode:1936ПхРв ... 50.1066П. Дои:10.1103 / PhysRev.50.1066.
34. Williams, E .; Faller, J .; Хилл, Х. (1971). "Новый экспериментальный тест закона Кулона: лабораторный верхний предел массы покоя фотона". Письма с физическими проверками. 26 (12): 721. Bibcode:1971PhRvL..26..721W. Дои:10.1103 / PhysRevLett.26.721.
35. Чибисов, Г В (1976). «Верхние астрофизические пределы массы покоя фотона». Успехи советской физики.. 19 (7): 624. Bibcode:1976СвФУ..19..624С. Дои:10.1070 / PU1976v019n07ABEH005277.
36. Озера, Родерик (1998). "Экспериментальные пределы массы фотона и космического магнитного векторного потенциала". Письма с физическими проверками. 80 (9): 1826. Bibcode:1998ПхРвЛ..80.1826Л. Дои:10.1103 / PhysRevLett.80.1826.
37. Амслер, К; Дозер, М; Антонелли, М; Аснер, Д; Бабу, К; Baer, ​​H; Band, H; Barnett, R; и другие. (2008). «Обзор физики элементарных частиц⁎» (PDF). Письма по физике B. 667 (1–5): 1. Bibcode:2008ФЛБ..667 .... 1А. Дои:10.1016 / j.physletb.2008.07.018. Таблица результатов
38. Адельбергер, Эрик; Двали, Гиа; Грузинов, Андрей (2007). «Связанная фотонной массой разрушается вихрями». Письма с физическими проверками. 98 (1): 010402. arXiv:hep-ph / 0306245. Bibcode:2007PhRvL..98a0402A. Дои:10.1103 / PhysRevLett.98.010402. PMID  17358459.
39. Декарт, Р. (1637). Discours de la méthode (Беседа о методе) (На французском). Imprimerie de Ian Maire. ISBN  978-0-268-00870-3.
40. Гук, Р. (1667). Микрография: или некоторые физиологические описания мельчайших тел, сделанные с помощью луп, с наблюдениями и исследованиями по ним ... Лондон: Лондонское королевское общество. ISBN  978-0-486-49564-4.
41. Гюйгенс, К. (1678). Traité de la lumière (На французском).. An английский перевод доступен из Проект Гутенберг
42. Ньютон, И. (1952) [1730]. Opticks (4-е изд.). Дувр, Нью-Йорк: Публикации Дувра. Книга II, Часть III, Предложения XII – XX, Вопросы 25–29. ISBN  978-0-486-60205-9.
43. Бухвальд, Дж. (1989). Возникновение волновой теории света: оптическая теория и эксперимент в начале девятнадцатого века. Физика сегодня. 43. Издательство Чикагского университета. С. 78–80. Bibcode:1990ФТ .... 43д..78Б. Дои:10.1063/1.2810533. ISBN  978-0-226-07886-1. OCLC  18069573.
44. Максвелл, Дж. (1865). «Динамическая теория электромагнитного поля». Философские труды Королевского общества. 155: 459–512. Bibcode:1865РСПТ..155..459С. Дои:10.1098 / рстл.1865.0008. Эта статья последовала за презентацией Максвелла Королевскому обществу 8 декабря 1864 года.
45. Герц, Х. (1888). "Über Strahlen elektrischer Kraft". Sitzungsberichte der Preussischen Akademie der Wissenschaften (Берлин) (на немецком). 1888: 1297–1307.
46. Частотная зависимость свечения стр. 276ff., Раздел фотоэффекта 1.4 в Алонсо и Финн 1968
47. Вена, В. (1911). "Нобелевская лекция Вильгельма Вена". nobelprize.org.
48. Планк, М. (1901). "Über das Gesetz der Energieverteilung im Normalspectrum". Annalen der Physik (на немецком). 4 (3): 553–563. Bibcode:1901АнП ... 309..553П. Дои:10.1002 / andp.19013090310. английский перевод
49. Планк, М. (1920). "Нобелевская лекция Макса Планка". nobelprize.org.
50. Эйнштейн, А. (1909). "Über die Entwicklung unserer Anschauungen über das Wesen und die Konstitution der Strahlung" (PDF). Physikalische Zeitschrift (на немецком). 10: 817–825.. An английский перевод доступен из Wikisource.
51. Презентационная речь Сванте Аррениус на присуждение Нобелевской премии по физике 1921 г., 10 декабря 1922 г. Текст онлайн из [nobelprize.org], Нобелевский фонд, 2008. Дата обращения 05.12.2008.
52. Эйнштейн, А. (1916). "Zur Quantentheorie der Strahlung". Mitteilungen der Physikalischen Gesellschaft zu Zürich. 16: 47. Также Physikalische Zeitschrift, 18, 121–128 (1917). (на немецком)
53. Комптон, А. (1923). «Квантовая теория рассеяния рентгеновских лучей на элементах света». Физический обзор. 21 (5): 483–502. Bibcode:1923ПхРв ... 21..483С. Дои:10.1103 / PhysRev.21.483.
54. Пайс, А. (1982). Тонкость - это Господь: наука и жизнь Альберта Эйнштейна. Издательство Оксфордского университета. ISBN  978-0-19-853907-0.
55. Милликен Р.А. (1924). "Нобелевская лекция Роберта А. Милликена".
56. Хендри, Дж. (1980). «Развитие взглядов на волновой дуализм света и квантовой теории, 1900–1920 годы». Анналы науки. 37 (1): 59–79. Дои:10.1080/00033798000200121.
57. Бор, Н.; Крамерс, Х.А.; Слейтер, Дж. (1924). «Квантовая теория излучения». Философский журнал. 47 (281): 785–802. Дои:10.1080/14786442408565262. Также Zeitschrift für Physik, 24, 69 (1924).
58. Ховард, Дон (декабрь 2004 г.). «Кто изобрел« Копенгагенскую интерпретацию »? Этюд по мифологии». Философия науки. 71 (5): 669–682. Дои:10.1086/425941. ISSN  0031-8248. JSTOR  10.1086/425941.
59. Гейзенберг, В. (1933). «Нобелевская лекция Гейзенберга».
60. Мандель, Л. (1976). Э. Вольф (ред.). Аргументы за и против полуклассической теории излучения. Прогресс в оптике. Прогресс в оптике. 13. Северная Голландия. С. 27–69. Bibcode:1976ПрОпт..13 ... 27М. Дои:10.1016 / S0079-6638 (08) 70018-0. ISBN  978-0-444-10806-7.
61. Тейлор, Г. (1909). Интерференционные полосы при слабом свете. Труды Кембриджского философского общества. 15. С. 114–115.
62. Салех, Б.Е.А. И Тейч, М. (2007). Основы фотоники. Вайли. ISBN  978-0-471-35832-9.
63. Ньютон, Т.Д .; Вигнер, Э. (1949). «Локализованные состояния элементарных частиц» (PDF). Обзоры современной физики. 21 (3): 400–406. Bibcode:1949РвМП ... 21..400Н. Дои:10.1103 / RevModPhys.21.400.
64. Бялыницкий-Бирула, И. (1994). «О волновой функции фотона» (PDF). Acta Physica Polonica A. 86 (1–2): 97–116. Дои:10.12693 / APhysPolA.86.97.
65. Сайпе, Дж. Э. (1995). «Волновые функции фотона». Физический обзор A. 52 (3): 1875–1883. Bibcode:1995PhRvA..52.1875S. Дои:10.1103 / PhysRevA.52.1875. PMID  9912446.
66. Бялыницкий-Бирула, И. (1996). Волновая функция фотона. Прогресс в оптике. Прогресс в оптике. 36. С. 245–294. Bibcode:1996ПрОпт..36..245Б. Дои:10.1016 / S0079-6638 (08) 70316-0. ISBN  978-0-444-82530-8.
67. Скалли, M.O .; Зубайри, М. (1997). Квантовая оптика. Кембридж: Издательство Кембриджского университета. ISBN  978-0-521-43595-6.
68. Буш, Пол; Лахти, Пекка; Вернер, Рейнхард Ф. (2013-10-17). «Доказательство связи Гейзенберга ошибка-возмущение» (PDF). Письма с физическими проверками. 111 (16): 160405. Дои:10.1103 / PhysRevLett.111.160405. ISSN  0031-9007. PMID  24182239.
69. Эпплби, Дэвид Маркус (2016-05-06). «Квантовые ошибки и возмущения: ответ Бушу, Лахти и Вернеру». Энтропия. 18 (5): 174. Дои:10.3390 / e18050174.
70. Ландау, Л.; Лифшиц, Э. (1977). Квантовая механика: нерелятивистская теория. Vol. 3 (3-е изд.). Pergamon Press. ISBN  978-0-08-020940-1. OCLC  2284121.
71. Busch, P .; Грабовский, М .; Лахти, П.Дж. (январь 1995 г.). «Кто боится мер POV? Единый подход к квантовым фазовым наблюдаемым». Анналы физики. 237 (1): 1–11. Дои:10.1006 / aphy.1995.1001.
72. Бозе, С. (1924). "Plancks Gesetz und Lichtquantenhypothese". Zeitschrift für Physik (на немецком). 26 (1): 178–181. Bibcode:1924ZPhy ... 26..178B. Дои:10.1007 / BF01327326.
73. Эйнштейн, А. (1924). "Quantentheorie des einatomigen idealen Gases". Sitzungsberichte der Preussischen Akademie der Wissenschaften (Берлин), Physikalisch-Mathematische Klasse (на немецком). 1924: 261–267.
74. Эйнштейн, А. (1925). Quantentheorie des einatomigen idealen Gases, Zweite Abhandlung. Sitzungsberichte der Preussischen Akademie der Wissenschaften (Берлин), Physikalisch-Mathematische Klasse (на немецком). 1925. С. 3–14. Дои:10.1002 / 3527608958.ch28. ISBN  978-3-527-60895-9.
75. Андерсон, M.H .; Ensher, J.R .; Matthews, M.R .; Виман, К.; Корнелл, Э.А. (1995). "Наблюдение конденсации Бозе – Эйнштейна в разбавленном атомном паре". Наука. 269 (5221): 198–201. Bibcode:1995Научный ... 269..198A. Дои:10.1126 / science.269.5221.198. JSTOR  2888436. PMID  17789847.
76. "Физики медленной скорости света". News.harvard.edu (18 февраля 1999 г.). Проверено 11 мая 2015.
77. «Свет превратился в материю, затем остановился и переместился». photonics.com (февраль 2007 г.). Проверено 11 мая 2015.
78. Streater, R.F .; Вайтман, А. (1989). PCT, спин, статистика и все такое. Эддисон-Уэсли. ISBN  978-0-201-09410-7.
79. Эйнштейн, А. (1916). "Strahlungs-эмиссия и поглощение nach der Quantentheorie". Verhandlungen der Deutschen Physikalischen Gesellschaft (на немецком). 18: 318–323. Bibcode:1916DPhyG..18..318E.
80. Раздел 1.4 в Wilson, J .; Хоукс, Ф.Дж. (1987). Лазеры: принципы и применение. Нью-Йорк: Прентис-Холл. ISBN  978-0-13-523705-2.
81. Эйнштейн, А. (1916). "Strahlungs-эмиссия и поглощение nach der Quantentheorie". Verhandlungen der Deutschen Physikalischen Gesellschaft (на немецком). 18: 318–323. Bibcode:1916DPhyG..18..318E. п. 322: Die Konstanten ${displaystyle A_{m}^{n}}$ и ${displaystyle B_{m}^{n}}$ würden sich direkt berechnen lassen, wenn wir im Besitz einer im Sinne der Quantenhypothese modifizierten Elektrodynamik und Mechanik wären. "
82. Дирак, П.А. (1926). «К теории квантовой механики». Труды Королевского общества А. 112 (762): 661–677. Bibcode:1926RSPSA.112..661D. Дои:10.1098 / rspa.1926.0133.
83. Дирак, П.А. (1927). «Квантовая теория излучения и поглощения излучения». Труды Королевского общества А. 114 (767): 243–265. Bibcode:1927RSPSA.114..243D. Дои:10.1098 / RSPA.1927.0039.
84. Дирак, П.А. (1927b). Квантовая теория дисперсии. Труды Королевского общества А. 114. С. 710–728. Bibcode:1927RSPSA.114..710D. Дои:10.1098 / RSPA.1927.0071.
85. Гейзенберг, В.; Паули, В. (1929). "Zur Quantentheorie der Wellenfelder". Zeitschrift für Physik (на немецком). 56 (1–2): 1. Bibcode:1929ZPhy ... 56 .... 1H. Дои:10.1007 / BF01340129.
86. Гейзенберг, В.; Паули, В. (1930). "Zur Quantentheorie der Wellenfelder". Zeitschrift für Physik (на немецком). 59 (3–4): 139. Bibcode:1930ZPhy ... 59..168H. Дои:10.1007 / BF01341423.
87. Ферми, Э. (1932). «Квантовая теория излучения». Обзоры современной физики. 4 (1): 87. Bibcode:1932РвМП .... 4 ... 87Ф. Дои:10.1103 / RevModPhys.4.87.
88. Родился М. (1926). "Zur Quantenmechanik der Stossvorgänge". Zeitschrift für Physik (на немецком). 37 (12): 863–867. Bibcode:1926ZPhy ... 37..863B. Дои:10.1007 / BF01397477.
89. Родился М. (1926). "Quantenmechanik der Stossvorgänge". Zeitschrift für Physik (на немецком). 38 (11–12): 803. Bibcode:1926ZPhy ... 38..803B. Дои:10.1007 / BF01397184.
90. Пайс, А. (1986). Внутренняя связь: материи и сил в физическом мире. Издательство Оксфордского университета. п. 260. ISBN  978-0-19-851997-3. В частности, Борн утверждал, что его вдохновили никогда не публиковавшиеся попытки Эйнштейна разработать теорию «призрачного поля», в которой точечные фотоны вероятностно управляются призрачными полями, которые следуют уравнениям Максвелла.
91. Дебай, П. (1910). "Der Wahrscheinlichkeitsbegriff in der Theorie der Strahlung". Annalen der Physik (на немецком). 33 (16): 1427–1434. Bibcode:1910AnP ... 338.1427D. Дои:10.1002 / andp.19103381617.
92. Родился М.; Гейзенберг, В.; Джордан, П. (1925). «Квантенмеханик II». Zeitschrift für Physik (на немецком). 35 (8–9): 557–615. Bibcode:1926ZPhy ... 35..557B. Дои:10.1007 / BF01379806.
93. Зи, Энтони (2003). Квантовая теория поля в двух словах. Принстон, штат Нью-Джерси: Princeton University Press. ISBN  0-691-01019-6. OCLC  50479292.
94. Фотон – фотонное рассеяние, раздел 7-3-1, перенормировка, глава 8-2 в Itzykson, C .; Зубер, Ж.-Б. (1980). Квантовая теория поля. Макгроу-Хилл. ISBN  978-0-07-032071-0.
95. Вейглейн, Г. (2008). «Электрослабая физика в ILC». Journal of Physics: Серия конференций. 110 (4): 042033. arXiv:0711.3003. Bibcode:2008JPhCS.110d2033W. Дои:10.1088/1742-6596/110/4/042033.
96. Райдер, Л. Х. (1996). Квантовая теория поля (2-е изд.). Издательство Кембриджского университета. ISBN  978-0-521-47814-4.
97. Нобелевская лекция Шелдона Глэшоу, доставлен 8 декабря 1979 г.
98. Лекция Абдуса Салама Нобеля, доставлен 8 декабря 1979 г.
99. Нобелевская лекция Стивена Вайнберга, доставлен 8 декабря 1979 г.
100. Например, глава 14 в Хьюз, И. (1985). Элементарные частицы (2-е изд.). Издательство Кембриджского университета. ISBN  978-0-521-26092-3.
101. Bauer, T.H .; Spital, R.D .; Йенни, Д.Р .; Пипкин, Ф. (1978). «Адронные свойства фотона при взаимодействии высоких энергий». Обзоры современной физики. 50 (2): 261. Bibcode:1978РвМП ... 50..261Б. Дои:10.1103 / RevModPhys.50.261.
102. Сакураи, Дж. Дж. (1960). «Теория сильных взаимодействий». Анналы физики. 11 (1): 1–48. Bibcode:1960АнФи..11 .... 1С. Дои:10.1016/0003-4916(60)90126-3.
103. Walsh, T.F .; Зервас, П. (1973). «Двухфотонные процессы в партонной модели». Письма по физике B. 44 (2): 195. Bibcode:1973ФЛБ ... 44..195Вт. Дои:10.1016/0370-2693(73)90520-0.
104. Виттен, Э. (1977). «Аномальное сечение фотон-фотонного рассеяния в калибровочных теориях». Ядерная физика B. 120 (2): 189–202. Bibcode:1977НуФБ.120..189Вт. Дои:10.1016/0550-3213(77)90038-4.
105. Нисиус, Р. (2000). «Фотонная структура от глубоконеупругого электрон-фотонного рассеяния». Отчеты по физике. 332 (4–6): 165–317. arXiv:hep-ex / 9912049. Bibcode:2000ФР ... 332..165Н. Дои:10.1016 / S0370-1573 (99) 00115-5.
106. Например, раздел 10.1 в Данлэп, Р.А. (2004). Введение в физику ядер и частиц. Брукс / Коул. ISBN  978-0-534-39294-9.
107. Радиационная поправка к секции массы электронов 7-1-2, секции аномальных магнитных моментов 7-2-1, секции лэмбовского сдвига 7-3-2 и сверхтонкого расщепления в секции позитрония 10-3 дюйма Itzykson, C .; Зубер, Ж.-Б. (1980). Квантовая теория поля. Макгроу-Хилл. ISBN  978-0-07-032071-0.
108. Например. разделы 9.1 (гравитационный вклад фотонов) и 10.5 (влияние гравитации на свет) в Stephani, H .; Стюарт, Дж. (1990). Общая теория относительности: введение в теорию гравитационного поля. Издательство Кембриджского университета. С. 86 и сл., 108 и далее. ISBN  978-0-521-37941-0.
109. Секция поляритонов 10.10.1, секция комбинационного рассеяния и бриллюэна 10.11.3 в Patterson, J.D .; Бейли, Британская Колумбия (2007). Физика твердого тела: введение в теорию. Springer. ISBN  978-3-540-24115-7.
110. Naeye, R. (1998). Глазами Хаббла: рождение, жизнь и насильственная смерть звезд. CRC Press. ISBN  978-0-7503-0484-9. OCLC  40180195.
111. Купелис, Тео; Кун, Карл Ф. (2007). В поисках Вселенной. Джонс и Бартлетт Канада. п. 102. ISBN  9780763743871.
112. Например. раздел 11-5 C в Pine, S.H .; Хендриксон, J.B .; Cram, D.J .; Хаммонд, Г.С. (1980). Органическая химия (4-е изд.). Макгроу-Хилл. ISBN  978-0-07-050115-7.
113. Нобелевская лекция, прочитанная Дж. Вальдом 12 декабря 1967 г., на сайте nobelprize.org: Молекулярные основы визуального возбуждения.
114. Секция фотоумножителя 1.1.10, секция ПЗС 1.1.8, секция счетчиков Гейгера 1.3.2.1 дюйма Китчин, C.R. (2008). Астрофизические методы. Бока-Ратон, Флорида: CRC Press. ISBN  978-1-4200-8243-2.
115. Уэймут, Джон (1971). Электрические газоразрядные лампы. Кембридж, Массачусетс: M.I.T. Нажмите. ISBN  978-0-262-23048-3.
116. Denk, W .; Свобода, К. (1997). «Превосходство фотонов: почему многофотонная визуализация - это больше, чем просто уловка». Нейрон. 18 (3): 351–357. Дои:10.1016 / S0896-6273 (00) 81237-4. PMID  9115730.
117. Лакович, Дж. Р. (2006). Принципы флуоресцентной спектроскопии. Springer. стр. 529 и сл. ISBN  978-0-387-31278-1.
118. Jennewein, T .; Achleitner, U .; Weihs, G .; Weinfurter, H .; Цайлингер, А. (2000). «Быстрый и компактный квантовый генератор случайных чисел». Обзор научных инструментов. 71 (4): 1675–1680. arXiv:Quant-ph / 9912118. Bibcode:2000RScI ... 71.1675J. Дои:10.1063/1.1150518.
119. Стефанов, А .; Гисин, Н .; Guinnard, O .; Guinnard, L .; Збиден, Х. (2000). «Оптический квантовый генератор случайных чисел». Журнал современной оптики. 47 (4): 595–598. Дои:10.1080/095003400147908.
120. Хигнетт, Кэтрин (16 февраля 2018 г.). «Физика создает новую форму света, которая может привести к революции квантовых вычислений». Newsweek. Получено 17 февраля 2018.
121. Лян, Ци-Ю; и другие. (16 февраля 2018 г.). «Наблюдение трехфотонных связанных состояний в квантовой нелинейной среде». Наука. 359 (6377): 783–786. arXiv:1709.01478. Bibcode:2018Научный ... 359..783L. Дои:10.1126 / science.aao7293. ЧВК  6467536. PMID  29449489.

дальнейшее чтение

По дате публикации:

• Алонсо, М .; Финн, Э.Дж. (1968). Фундаментальная университетская физика Том III: Квантовая и статистическая физика. Эддисон-Уэсли. ISBN  978-0-201-00262-1.
• Клаузер, Дж. Ф. (1974). «Экспериментальное различие между квантовыми и классическими теоретико-полевыми предсказаниями фотоэлектрического эффекта». Физический обзор D. 9 (4): 853–860. Bibcode:1974ПХРВД ... 9..853С. Дои:10.1103 / PhysRevD.9.853.
• Пайс, А. (1982). Тонкость - это Господь: наука и жизнь Альберта Эйнштейна. Издательство Оксфордского университета.
• Фейнман, Ричард (1985). QED: странная теория света и материи. Издательство Принстонского университета. ISBN  978-0-691-12575-6.
• Grangier, P .; Roger, G .; Аспект, А. (1986). «Экспериментальные доказательства эффекта антикорреляции фотонов на светоделителе: новый свет на однофотонные помехи». Письма еврофизики. 1 (4): 173–179. Bibcode:1986EL ...... 1..173G. CiteSeerX  10.1.1.178.4356. Дои:10.1209/0295-5075/1/4/004.
• Lamb, W.E. (1995). «Антифотон». Прикладная физика B. 60 (2–3): 77–84. Bibcode:1995АпФБ..60 ... 77л. Дои:10.1007 / BF01135846.
• Специальный дополнительный выпуск журнала Новости оптики и фотоники (том 14, октябрь 2003 г.) ссылка на статью
  • Roychoudhuri, C .; Раджарши, Р. (2003). «Природа света: что такое фотон?». Новости оптики и фотоники. 14: S1 (Приложение).
  • Зайонц, А. «Свет по-новому». Новости оптики и фотоники. 14: S2 – S5 (Приложение).
  • Лаудон, Р. «Что такое фотон?». Новости оптики и фотоники. 14: S6 – S11 (Приложение).
  • Финкельштейн Д. Что такое фотон? Новости оптики и фотоники. 14: S12 – S17 (Приложение).
  • Muthukrishnan, A .; Скалли, M.O .; Зубайри, М. «Новое в концепции фотона». Новости оптики и фотоники. 14: S18 – S27 (Приложение).
  • Mack, H .; Schleich, W.P. «Фотон из фазового пространства Вигнера». Новости оптики и фотоники. 14: S28 – S35 (Приложение).
• Глаубер, Р. (2005). "Сто лет светлой кванты" (PDF). Лекция 2005 г. по физике. Архивировано из оригинал (PDF) на 2008-07-23. Получено 2009-06-29.
• Хентшель, К. (2007). «Кванты света: созревание концепции путем постепенного увеличения значения». Физика и философия. 1 (2): 1–20.

Обучение одиночными фотонами:

• Thorn, J.J .; Neel, M.S .; Донато, В.В .; Bergreen, G.S .; Davies, R.E .; Бек, М. (2004). «Наблюдение за квантовым поведением света в студенческой лаборатории» (PDF). Американский журнал физики. 72 (9): 1210–1219. Bibcode:2004AmJPh..72.1210T. Дои:10.1119/1.1737397.
• Bronner, P .; Струнц, Андреас; Зильберхорн, Кристина; Мейн, Ян-Питер (2009). «Интерактивные экранные эксперименты с одиночными фотонами». Европейский журнал физики. 30 (2): 345–353. Bibcode:2009EJPh ... 30..345B. Дои:10.1088/0143-0807/30/2/014.

внешняя ссылка

• Котировки, связанные с Фотон в Викицитатнике
• Словарное определение фотон в Викисловарь
• СМИ, связанные с Фотон в Wikimedia Commons