Точка зрения - Frame of reference

Не путать с Инерциальная система отсчета.

Для использования в других целях см. Система отсчета (значения).

В физика, а точка зрения (или же система отсчета) состоит из абстрактного система координат и набор физических опорных точек, которые однозначно фиксируют (определяют местоположение и ориентируют) систему координат и стандартизируют измерения в пределах этого кадра^{[нужна цитата ]}.

За п размеры, п + 1 контрольных точек достаточно, чтобы полностью определить систему отсчета. С помощью прямоугольные (декартовы) координаты, Опорный кадр может быть определен с опорной точкой в ​​начале координат и опорной точкой на одном единицу расстояния вдоль каждого из п оси координат^{[нужна цитата ]}.

В Эйнштейновская теория относительности, системы отсчета используются для определения отношения между движущимися наблюдатель и наблюдаемое явление или явления. В этом контексте фраза часто становится "система наблюдения" (или же "система отсчета наблюдений"), что означает, что наблюдатель покоится в кадре, хотя и не обязательно в его источник. Релятивистская система отсчета включает (или подразумевает) координировать время, что не соответствует разным кадрам движение относительно друг другу. Таким образом, ситуация отличается от Галилея относительность, где все возможные координатные времена по существу эквивалентны^{[нужна цитата ]}.

Различные аспекты «системы отсчета»

Необходимость различать различные значения «системы отсчета» привела к появлению множества терминов. Например, иногда тип системы координат присоединяется как модификатор, как в Декартова система отсчета. Иногда подчеркивается состояние движения, как в вращающаяся система отсчета. Иногда то, как он трансформируется в кадры, считающиеся связанными, подчеркивается, как в Галилеевская система отсчета. Иногда кадры различаются масштабом наблюдений, как в макроскопический и микроскопические системы отсчета.^[1]

В этой статье термин система наблюдения используется, когда акцент делается на состояние движения а не от выбора координат или характера наблюдений или наблюдательной аппаратуры. В этом смысле система координат наблюдений позволяет изучать влияние движения на все семейство систем координат, которые могут быть присоединены к этой системе координат. С другой стороны, система координат может использоваться для многих целей, где состояние движения не является основной задачей. Например, система координат может быть принята, чтобы воспользоваться преимуществом симметрии системы. В еще более широкой перспективе при постановке многих задач физики используются обобщенные координаты, нормальные режимы или же собственные векторы, которые лишь косвенно связаны с пространством и временем. Представляется полезным разделить различные аспекты системы отсчета для обсуждения ниже. Поэтому мы принимаем системы координат наблюдений, системы координат и оборудование для наблюдений как независимые концепции, разделенные следующим образом:

• Рамка наблюдения (например, инерциальная система отсчета или же неинерциальная система отсчета ) - это физическое понятие, связанное с состоянием движения.
• Система координат - это математическое понятие, означающее выбор языка, используемого для описания наблюдений.^[2] Следовательно, наблюдатель в системе отсчета наблюдений может выбрать использование любой системы координат (декартовой, полярной, криволинейной, обобщенной…) для описания наблюдений, сделанных из этой системы отсчета. Изменение выбора этой системы координат не меняет состояния движения наблюдателя и, следовательно, не влечет за собой изменения его состояния. наблюдательный точка зрения. Эту точку зрения можно найти и в другом месте.^[3] Это не означает, что некоторые системы координат могут быть лучшим выбором для одних наблюдений, чем другие.

• Выбор того, что измерять и с помощью какой аппаратуры наблюдения, - это вопрос, отдельный от состояния движения наблюдателя и выбора системы координат.

Вот цитата, применимая к движущимся рамкам наблюдения ${\displaystyle {\mathfrak {R}}}$ и различные связанные евклидовы трехпространственные системы координат [р, Р', и Т. Д.]:^[4]

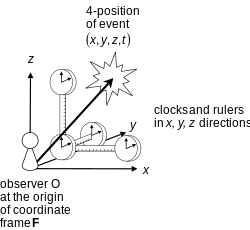
Сначала введем понятие система отсчета, сама связана с идеей наблюдатель: система отсчета - это, в некотором смысле, «евклидово пространство, переносимое наблюдателем». Давайте дадим более математическое определение:… система отсчета - это… множество всех точек в евклидовом пространстве с движением твердого тела наблюдателя. Рамка, обозначенная ${\displaystyle {\mathfrak {R}}}$, говорят, движется вместе с наблюдателем.… Пространственные положения частиц помечены относительно кадра ${\displaystyle {\mathfrak {R}}}$ путем создания система координат р с происхождением О. Соответствующий набор осей, разделяющих движение твердого тела рамы ${\displaystyle {\mathfrak {R}}}$, можно рассматривать как физическую реализацию ${\displaystyle {\mathfrak {R}}}$. В кадре ${\displaystyle {\mathfrak {R}}}$, координаты меняются с р к Р' выполняя в каждый момент времени одно и то же преобразование координат на компонентах внутренний объекты (векторы и тензоры), введенные для представления физических величин в этом кадре.

и это о полезности разделения понятий ${\displaystyle {\mathfrak {R}}}$ и [р, Р', и Т. Д.]:^[5]

Как отмечал Бриллюэн, необходимо различать математические наборы координат и физические системы отсчета. Незнание такого различия является источником большой путаницы ... зависимые функции, такие как, например, скорость, измеряются относительно физической системы отсчета, но можно выбрать любую математическую систему координат, в которой заданы уравнения.

и это, а также различие между ${\displaystyle {\mathfrak {R}}}$ и [р, Р', и Т. Д.]:^[6]

Идея системы отсчета действительно сильно отличается от концепции системы координат. Рамки различаются только тогда, когда они определяют разные пробелы (наборы отдых баллов) или времени (наборы одновременных событий). Итак, идеи пространства, времени, покоя и одновременности неразрывно связаны с концепцией фрейма. Однако простое смещение начала координат или чисто пространственное вращение пространственных координат приводит к новой системе координат. Так что кадры в лучшем случае соответствуют классы систем координат.

и от Дж. Д. Нортона:^[7]

В традиционных разработках специальной и общей теории относительности было принято не различать две совершенно разные идеи. Первый - это понятие системы координат, понимаемое просто как плавное, обратимое присвоение четырех чисел событиям в окрестностях пространства-времени. Вторая, система отсчета, относится к идеализированной системе, используемой для присвоения таких чисел […] Чтобы избежать ненужных ограничений, мы можем отделить это расположение от метрических понятий. […] Для наших целей особенно важно то, что каждая система отсчета имеет определенное состояние движения в каждом событии пространства-времени. […] В контексте специальной теории относительности и до тех пор, пока мы ограничиваемся системами отсчета при инерционном движении, мало важности зависит от разницы между инерциальной системой отсчета и инерциальной системой координат, которую она создает. Это удобное обстоятельство исчезает сразу же, как только мы начинаем рассматривать системы отсчета при неоднородном движении даже в рамках специальной теории относительности ... В последнее время, чтобы преодолеть очевидную двусмысленность трактовки Эйнштейна, понятие системы отсчета вновь появилось как структура, отличная от системы координат. .

Обсуждение выходит за рамки простых систем координат пространства-времени Брэдингом и Кастеллани.^[8] Распространение на системы координат с использованием обобщенных координат лежит в основе Гамильтониан и Лагранжиан составы^[9] из квантовая теория поля, классическая релятивистская механика, и квантовая гравитация.^{[10][11][12][13][14]}

Системы координат

Основная статья: Системы координат

Смотрите также: Обобщенные координаты и Соглашения об осях

Наблюдатель O, расположенный в начале локального набора координат - системы отсчета F. Наблюдатель в этом кадре использует координаты (х, у, г, т) для описания пространственно-временного события, изображенного звездой.

Хотя термин «система координат» часто используется (особенно физиками) в нетехническом смысле, термин «система координат» действительно имеет точное значение в математике, а иногда и физики имеют в виду именно это.

Система координат в математике - это аспект геометрия или из алгебра,^[15][16] в частности, свойство коллекторы (например, в физике, конфигурационные пространства или же фазовые пространства ).^[17][18] В координаты точки р в п-мерное пространство - это просто упорядоченный набор п числа:^[19][20]

${\displaystyle \mathbf {r} =[x^{1},\ x^{2},\ \dots ,\ x^{n}].}$

В общем Банахово пространство, эти числа могут быть (например) коэффициентами в функциональном разложении, таком как Ряд Фурье. В физической проблеме они могли быть пространство-время координаты или нормальный режим амплитуды. В дизайн робота, это могут быть углы относительного поворота, линейного смещения или деформации суставы.^[21] Здесь мы предположим, что эти координаты могут быть связаны с Декартова координата система набором функций:

${\displaystyle x^{j}=x^{j}(x,\ y,\ z,\ \dots ),\quad j=1,\ \dots ,\ n,}$

куда Икс, у, z, и Т. Д. являются п Декартовы координаты точки. Учитывая эти функции, координатные поверхности определяются отношениями:

${\displaystyle x^{j}(x,y,z,\dots )=\mathrm {constant} ,\quad j=1,\ \dots ,\ n.}$

Пересечение этих поверхностей определяет координатные линии. В любой выбранной точке касательные к пересекающимся координатным линиям в этой точке определяют набор базисные векторы {е₁, е₂, …, е_п} в таком случае. То есть:^[22]

${\displaystyle \mathbf {e} _{i}(\mathbf {r} )=\lim _{\epsilon \rightarrow 0}{\frac {\mathbf {r} \left(x^{1},\ \dots ,\ x^{i}+\epsilon ,\ \dots ,\ x^{n}\right)-\mathbf {r} \left(x^{1},\ \dots ,\ x^{i},\ \dots ,\ x^{n}\right)}{\epsilon }},\quad i=1,\ \dots ,\ n,}$

которая может быть нормализована до единичной длины. Подробнее см. криволинейные координаты.

Координатные поверхности, координатные линии и базисные векторы компоненты система координат.^[23] Если базисные векторы ортогональны в каждой точке, система координат является ортогональная система координат.

Важным аспектом системы координат является ее метрический тензор грамм_ik, что определяет длина дуги ds в системе координат через ее координаты:^[24]

${\displaystyle (ds)^{2}=g_{ik}\ dx^{i}\ dx^{k},}$

где суммируются повторяющиеся индексы.

Как видно из этих замечаний, система координат - это математическая конструкция, часть аксиоматическая система. Нет необходимой связи между системами координат и физическим движением (или любым другим аспектом реальности). Однако системы координат могут включать время в качестве координаты и могут использоваться для описания движения. Таким образом, Преобразования Лоренца и Галилеевы преобразования можно рассматривать как преобразования координат.

Общие и конкретные темы систем координат могут быть рассмотрены после Смотрите также ссылки ниже.

Системы наблюдения

Основная статья: Инерциальная система отсчета

Три системы отсчета в специальной теории относительности. Черная рамка покоится. Загрунтованная рамка движется со скоростью 40% скорости света, а двойная рамка - 80%. Обратите внимание на изменение, похожее на ножницы, при увеличении скорости.

An система наблюдения, часто называемый физическая система отсчета, а точка зрения, или просто Рамка, это физическая концепция, связанная с наблюдатель и состояние движения наблюдателя. Здесь мы принимаем точку зрения, выраженную Кумаром и Барве: система наблюдения характеризуется только по его состоянию движения.^[25] Однако по этому поводу нет единого мнения. В специальной теории относительности иногда проводится различие между наблюдатель и Рамка. Согласно этой точке зрения, Рамка является наблюдатель плюс координатная решетка, построенная как ортонормированный правый набор пространственноподобных векторов, перпендикулярных времениподобному вектору. См. Дорана.^[26] Этот ограниченный взгляд здесь не используется и не принимается повсеместно даже при обсуждении теории относительности.^[27][28] В общая теория относительности общепринято использование общих систем координат (см., например, Шварцшильд решение для гравитационного поля вне изолированной сферы^[29]).

Существует два типа системы отсчета наблюдений: инерционный и неинерциальный. Инерциальная система отсчета определяется как система, в которой все законы физики принимают свою простейшую форму. В специальная теория относительности эти кадры связаны Преобразования Лоренца, которые параметризованы быстрота. В механике Ньютона более ограниченное определение требует только того, что Первый закон Ньютона Справедливо; то есть ньютоновская инерциальная система отсчета - это система, в которой свободная частица путешествует в прямая линия при постоянном скорость, или находится в состоянии покоя. Эти кадры связаны Галилеевы преобразования. Эти релятивистские и ньютоновские преобразования выражаются в пространствах общей размерности через представления из Группа Пуанкаре и из Галилейская группа.

В отличие от инерциальной системы отсчета, неинерциальная система отсчета - это система, в которой фиктивные силы необходимо вызывать для объяснения наблюдений. Примером может служить система отсчета наблюдений с центром в точке на поверхности Земли. Эта система отсчета вращается вокруг центра Земли, что вводит фиктивные силы, известные как Сила Кориолиса, центробежная сила, и сила гравитации. (Все эти силы, включая гравитацию, исчезают в действительно инерциальной системе отсчета, которая является системой свободного падения.)

Измерительная аппаратура

Еще один аспект системы отсчета - это роль измерительная аппаратура (например, часы и стержни), прикрепленные к раме (см. цитату Нортона выше). Этот вопрос не рассматривается в данной статье и представляет особый интерес в квантовая механика, где связь между наблюдателем и измерением все еще обсуждается (см. проблема измерения ).

В физических экспериментах система отсчета, в которой неподвижны лабораторные измерительные приборы, обычно называется лабораторный каркас или просто "лабораторный фрейм". Примером может служить рамка, в которой детекторы ускорителя частиц находятся в покое. Лабораторный корпус в некоторых экспериментах является инерциальным, но это не обязательно (например, лаборатория на поверхности Земли во многих физических экспериментах не является инерциальной). В экспериментах по физике элементарных частиц часто бывает полезно преобразовывать энергии и импульсы частиц из лабораторной системы, на которой они измеряются, в центр импульса кадра «COM-кадр», в котором вычисления иногда упрощаются, поскольку потенциально вся кинетическая энергия, все еще присутствующая в COM-кадре, может быть использована для создания новых частиц.

В этой связи можно отметить, что часы и стержни, часто используемые для мысленного описания измерительного оборудования наблюдателей, на практике заменяются гораздо более сложными и косвенными. метрология это связано с природой вакуум, и использует атомные часы которые действуют в соответствии с стандартная модель и это нужно исправить для гравитационное замедление времени.^[30] (Видеть второй, метр и килограмм ).

Фактически, Эйнштейн считал, что часы и стержни были просто удобными измерительными устройствами, и их следует заменить более фундаментальными объектами, основанными, например, на атомах и молекулах.^[31]

Примеры инерциальных систем отсчета

Простой пример

Рисунок 1: Две машины, движущиеся с разными, но постоянными скоростями, наблюдаемые с неподвижной инерциальной системы координат. S прикрепленный к дороге и движущийся инерциальный каркас S ′ прикреплен к первой машине.

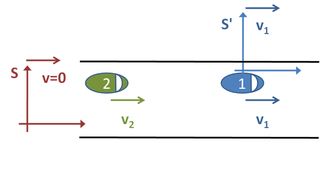
Рассмотрим ситуацию, обычную в повседневной жизни. По дороге едут две машины, обе движутся с постоянной скоростью. См. Рис. 1. В какой-то момент их разделяет 200 метров. Автомобиль впереди движется со скоростью 22 метра в секунду, а автомобиль позади него движется со скоростью 30 метров в секунду. Если мы хотим узнать, сколько времени потребуется второй машине, чтобы догнать первую, мы можем выбрать три очевидных «системы отсчета».

Сначала мы могли наблюдать за двумя машинами со стороны дороги. Мы определяем нашу «систему отсчета» S следующее. Мы стоим на обочине дороги и включаем секундомер в тот момент, когда нас проезжает вторая машина, а это бывает, когда они находятся на некотором расстоянии. d = 200 м Кроме. Поскольку ни одна из машин не ускоряется, мы можем определить их положение по следующим формулам, где ${\displaystyle x_{1}(t)}$ позиция в метрах автомобиля по очереди т за секунды и ${\displaystyle x_{2}(t)}$ это позиция машины два раза позже т.

${\displaystyle x_{1}(t)=d+v_{1}t=200+22t,\quad x_{2}(t)=v_{2}t=30t.}$

Обратите внимание, что эти формулы предсказывают на т = 0 с первая машина находится в 200 м по дороге, а вторая машина, как и ожидалось, прямо рядом с нами. Мы хотим найти время, в которое ${\displaystyle x_{1}=x_{2}}$. Поэтому положим ${\displaystyle x_{1}=x_{2}}$ и решить для ${\displaystyle t}$, то есть:

${\displaystyle 200+22t=30t,}$

${\displaystyle 8t=200,}$

${\displaystyle t=25\ \mathrm {seconds} .}$

В качестве альтернативы мы могли бы выбрать систему отсчета S ′ находится в первой машине. В этом случае первая машина стоит на месте, а вторая машина приближается сзади со скоростью v₂ − v₁ = 8 м / с. Чтобы догнать первую машину, потребуется время d/v₂ − v₁ = 200/8 s, то есть 25 секунд, как и раньше. Обратите внимание, насколько легче становится проблема, если выбрать подходящую систему координат. Третья возможная система отсчета будет привязана ко второй машине. Этот пример похож на только что рассмотренный случай, за исключением того, что второй вагон неподвижен, а первый движется к нему назад на 8 м / с.

Можно было бы выбрать вращающуюся, ускоряющуюся систему отсчета, двигающуюся сложным образом, но это могло бы излишне усложнить задачу. Также необходимо отметить, что можно переводить измерения, сделанные в одной системе координат, в другую. Например, предположим, что ваши часы идут на пять минут быстрее местного стандартного времени. Если вы знаете, что это так, когда кто-то спрашивает вас, который час, вы можете вычесть пять минут из времени, отображаемого на ваших часах, чтобы получить правильное время. Таким образом, измерения системы, производимые наблюдателем, зависят от системы координат наблюдателя (можно сказать, что автобус прибыл в 5 минут четвертого, хотя на самом деле он прибыл в три).

Дополнительный пример

Рисунок 2: Простой пример системы отсчета

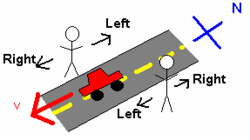
В качестве простого примера, включающего ориентацию только двух наблюдателей, представьте, что два человека стоят лицом друг к другу по обе стороны улицы с севера на юг. См. Рис. 2. Мимо них проезжает машина, направляющаяся на юг. Для человека, смотрящего на восток, машина двигалась вправо. Однако для человека, смотрящего на запад, машина двигалась влево. Это несоответствие связано с тем, что эти два человека использовали две разные системы отсчета для исследования этой системы.

В качестве более сложного примера с участием наблюдателей в относительном движении рассмотрим Альфреда, который стоит на обочине дороги и смотрит, как машина проезжает мимо него слева направо. В своей системе координат Альфред определяет точку, в которой он стоит, как исходную точку, дорогу как исходную точку. Икс-ось и направление перед ним как положительное у-ось. По его мнению, машина движется по Икс ось с некоторыми скорость v в положительном Икс-направление. Система отсчета Альфреда считается инерциальная система отсчета потому что он не ускоряется (игнорируя такие эффекты, как вращение Земли и гравитация).

Теперь рассмотрим Бетси, человека, ведущего машину. Бетси, выбирая систему отсчета, определяет свое местоположение как исходную точку, а направление вправо - как положительное. Иксось, а направление перед ней положительное у-ось. В этой системе координат Бетси неподвижна, а мир вокруг нее движется - например, проезжая мимо Альфреда, она наблюдает, как он движется со скоростью. v в отрицательном у-направление. Если она едет на север, то север будет положительным у-направление; если она повернет на восток, восток станет положительным у-направление.

Наконец, в качестве примера неинерциальных наблюдателей предположим, что Кэндис ускоряет свою машину. Когда она проходит мимо него, Альфред измеряет ее ускорение и находит это а в отрицательном Икс-направление. Предполагая, что ускорение Кэндис постоянно, какое ускорение измеряет Бетси? Если скорость Бетси v постоянна, она находится в инерциальной системе отсчета, и она обнаружит, что ускорение будет таким же, как у Альфреда в ее системе отсчета, а в отрицательном у-направление. Однако, если она ускоряется со скоростью А в отрицательном у-направлении (другими словами, замедление), она обнаружит, что ускорение Кэндис а ' = а − А в отрицательном у-направление - меньшее значение, чем измерил Альфред. Точно так же, если она ускоряется со скоростью А в положительном у-направлении (ускорение), она будет наблюдать ускорение Кэндис как а ' = а + А в отрицательном у-направление - большее значение, чем измерение Альфреда.

Ссылки особенно важны в специальная теория относительности, потому что, когда система отсчета движется со значительной долей скорости света, течение времени в этой системе не обязательно применяется в другой системе отсчета. Скорость света считается единственной истинной постоянной между движущимися системами отсчета.

Замечания

Смотрите также: Специальная теория относительности и Общая теория относительности

Важно отметить некоторые сделанные выше предположения относительно различных инерциальных систем отсчета. Ньютон, например, использовал всемирное время, как поясняет следующий пример. Предположим, что у вас есть два часа, которые идут с одинаковой скоростью. Вы синхронизируете их, чтобы они отображали одно и то же время. Теперь два часа разделены, и одни часы находятся в быстро движущемся поезде, движущемся с постоянной скоростью по направлению к другому. Согласно Ньютону, эти два часа по-прежнему будут идти с одинаковой скоростью и будут показывать одно и то же время. Ньютон говорит, что скорость времени, измеренная в одной системе отсчета, должна быть такой же, как скорость времени в другой. То есть существует «универсальное» время, и все остальные времена во всех других системах отсчета будут течь с той же скоростью, что и это универсальное время, независимо от их положения и скорости. Это понятие времени и одновременности было позже обобщено Эйнштейном в его работе. специальная теория относительности (1905), где он разработал преобразования между инерциальными системами отсчета, основанные на универсальной природе физических законов и их экономичности выражения (Преобразования Лоренца ).

Определение инерциальной системы отсчета также может быть расширено за пределы трехмерного евклидова пространства. Ньютон предполагал евклидово пространство, но общая теория относительности использует более общую геометрию. В качестве примера того, почему это важно, рассмотрим геометрия эллипсоида. В этой геометрии "свободная" частица определяется как неподвижная или движущаяся с постоянной скоростью по геодезический дорожка. Две свободные частицы могут начинаться в одной и той же точке на поверхности, перемещаясь с одинаковой постоянной скоростью в разных направлениях. Через некоторое время две частицы сталкиваются на противоположной стороне эллипсоида. Обе «свободные» частицы движутся с постоянной скоростью, удовлетворяя определению, что никакие силы не действуют. Ускорения не происходило, поэтому первый закон Ньютона был верен. Это означает, что частицы находились в инерциальных системах отсчета. Поскольку никакие силы не действовали, именно геометрия ситуации заставила две частицы снова встретиться друг с другом. Подобным образом сейчас принято описывать^[32] что мы существуем в четырехмерной геометрии, известной как пространство-время. На этом изображении кривизна этого четырехмерного пространства отвечает за то, как два тела с массой притягиваются вместе, даже если никакие силы не действуют. Это искривление пространства-времени заменяет силу, известную как гравитация в механике Ньютона и специальной теории относительности.

Неинерциальные кадры

Основные статьи: Фиктивная сила, Неинерциальный каркас, и Вращающаяся система отсчета

Здесь рассматривается связь между инерциальной и неинерциальной системами отсчета наблюдений. Основное различие между этими фреймами заключается в необходимости использования неинерциальных фреймов для фиктивных сил, как описано ниже.

Ускоренная система отсчета часто обозначается как «штрихованный» кадр, и все переменные, которые зависят от этого кадра, обозначаются штрихами, например Икс', y ′, а '.

Вектор от начала инерциальной системы отсчета до начала ускоренной системы отсчета обычно обозначается как р. Для данной точки интереса, которая существует в обоих кадрах, вектор от начала инерции до точки называется р, а вектор от ускоренного начала координат до точки называется р'. Из геометрии ситуации получаем

${\displaystyle \mathbf {r} =\mathbf {R} +\mathbf {r} '.}$

Беря первую и вторую производные от этого по времени, получаем

${\displaystyle \mathbf {v} =\mathbf {V} +\mathbf {v} ',}$

${\displaystyle \mathbf {a} =\mathbf {A} +\mathbf {a} '.}$

куда V и А - скорость и ускорение ускоряемой системы относительно инерциальной системы и v и а - скорость и ускорение точки интереса относительно инерциальной системы отсчета.

Эти уравнения допускают преобразования между двумя системами координат; например, теперь мы можем написать Второй закон Ньютона в качестве

${\displaystyle \mathbf {F} =m\mathbf {a} =m\mathbf {A} +m\mathbf {a} '.}$

Когда есть ускоренное движение из-за приложенной силы, есть проявление инерции. Если электромобиль, предназначенный для подзарядки своей аккумуляторной системы при замедлении, переключается на торможение, аккумуляторы перезаряжаются, демонстрируя физическую силу проявления инерции. Однако проявление инерции не предотвращает ускорение (или замедление), поскольку проявление инерции происходит в ответ на изменение скорости под действием силы. С точки зрения вращающейся системы координат проявление инерции, кажется, создает силу (либо в центробежный направлении или в направлении, ортогональном движению объекта, Эффект Кориолиса ).

Общий вид ускоренной системе отсчета представляет собой кадр, который является одновременно вращения и перемещения (примером может служить система отсчета прикреплен к компакт-диску, который играет, когда проигрыватель осуществляется). Такое расположение приводит к уравнению (см. Фиктивная сила для вывода):

${\displaystyle \mathbf {a} =\mathbf {a} '+{\dot {\boldsymbol {\omega }}}\times \mathbf {r} '+2{\boldsymbol {\omega }}\times \mathbf {v} '+{\boldsymbol {\omega }}\times ({\boldsymbol {\omega }}\times \mathbf {r} ')+\mathbf {A} _{0},}$

или, чтобы найти ускорение в ускоренном кадре,

${\displaystyle \mathbf {a} '=\mathbf {a} -{\dot {\boldsymbol {\omega }}}\times \mathbf {r} '-2{\boldsymbol {\omega }}\times \mathbf {v} '-{\boldsymbol {\omega }}\times ({\boldsymbol {\omega }}\times \mathbf {r} ')-\mathbf {A} _{0}.}$

Умножение на массу м дает

${\displaystyle \mathbf {F} '=\mathbf {F} _{\mathrm {physical} }+\mathbf {F} '_{\mathrm {Euler} }+\mathbf {F} '_{\mathrm {Coriolis} }+\mathbf {F} '_{\mathrm {centripetal} }-m\mathbf {A} _{0},}$

куда

${\displaystyle \mathbf {F} '_{\mathrm {Euler} }=-m{\dot {\boldsymbol {\omega }}}\times \mathbf {r} '}$ (Сила Эйлера ),

${\displaystyle \mathbf {F} '_{\mathrm {Coriolis} }=-2m{\boldsymbol {\omega }}\times \mathbf {v} '}$ (Сила Кориолиса ),

${\displaystyle \mathbf {F} '_{\mathrm {centrifugal} }=-m{\boldsymbol {\omega }}\times ({\boldsymbol {\omega }}\times \mathbf {r} ')=m(\omega ^{2}\mathbf {r} '-({\boldsymbol {\omega }}\cdot \mathbf {r} '){\boldsymbol {\omega }})}$ (центробежная сила ).

Конкретные общеупотребительные системы отсчета

• Международная наземная система отсчета
• Международная небесная система отсчета
• В гидромеханике Лагранжева и эйлерова спецификация поля течения

Другие кадры

• Поля кадра в общей теории относительности
• Лингвистическая система координат
• Подвижный фрейм в математике

Смотрите также

• Аналитическая механика
• Прикладная механика
• Декартова система координат
• Кадр с центром импульса
• Центробежная сила
• Центростремительная сила
• Классическая механика
• Сила Кориолиса
• Криволинейные координаты
• Динамика (физика)
• Формулы Френе – Серре
• Галилеевская инвариантность
• Общая теория относительности
• Обобщенные координаты
• Обобщенные силы
• Инерциальная система отсчета
• Материальный каркас-безразличие
• Тест стержня и рамы
• Кинематика
• Система координат лаборатории
• Преобразование Лоренца
• Принцип маха
• Ортогональные координаты
• Принцип относительности
• Квантовая система отсчета

Примечания

1. Различие между макроскопическими и микроскопическими кадрами проявляется, например, в электромагнетизме, где учредительные отношения различных шкал времени и длины используются для определения плотности тока и заряда, входящего в Уравнения Максвелла. См., Например, Курт Эдмунд Огстун (2006). Распространение электромагнитных и оптических импульсов 1: спектральные представления во временнодисперсных средах. Springer. п. 165. ISBN  0-387-34599-X.. Эти различия проявляются и в термодинамике. Видеть Пол Макэвой (2002). Классическая теория. MicroAnalytix. п. 205. ISBN  1-930832-02-8..
2. В очень общем виде система координат - это набор дуг Икс^я = Икс^я (т) в комплексе Группа Ли; видеть Лев Семенович Понтрягин (1986). Л.С. Понтрягин: Избранные произведения Т. 2: Топологические группы (3-е изд.). Гордон и Брич. п. 429. ISBN  2-88124-133-6.. Менее абстрактно система координат в пространстве n измерений определяется в терминах базисного набора векторов {е₁, е₂,… е_п}; видеть Эдоардо Сернези; Дж. Монтальди (1993). Линейная алгебра: геометрический подход. CRC Press. п. 95. ISBN  0-412-40680-2. Таким образом, система координат - это математическая конструкция, язык, который может быть связан с движением, но не имеет необходимой связи с движением.
3. J X Zheng-Johansson; Пер-Ивар Йоханссон (2006). Объединение классической, квантовой и релятивистской механики и четырех сил. Nova Publishers. п. 13. ISBN  1-59454-260-0.
4. Жан Саленсон; Стивен Лайл (2001). Справочник по механике сплошной среды: общие понятия, термоупругость. Springer. п. 9. ISBN  3-540-41443-6.
5. Патрик Корнилл (Ахлеш Лахтакия, редактор) (1993). Очерки формальных аспектов теории электромагнетизма. World Scientific. п. 149. ISBN  981-02-0854-5.
6. Грэм Нерлих (1994). Что объясняет пространство-время: метафизические очерки пространства и времени. Издательство Кембриджского университета. п. 64. ISBN  0-521-45261-9.
7. Джон Д. Нортон (1993). Общая ковариантность и основы общей теории относительности: восемь десятилетий споров, Rep. Prog. Phys., 56, стр. 835-7.
8. Кэтрин Брэдинг; Елена Кастеллани (2003). Симметрии в физике: философские размышления. Издательство Кембриджского университета. п. 417. ISBN  0-521-82137-1.
9. Оливер Дэвис Джонс (2005). Аналитическая механика для теории относительности и квантовой механики. Издательство Оксфордского университета. Глава 16. ISBN  0-19-856726-X.
10. Дональд Т. Гринвуд (1997). Классическая динамика (Перепечатка издания 1977 г., изд. Prentice-Hall ed.). Courier Dover Publications. п. 313. ISBN  0-486-69690-1.
11. Мэтью А. Трамп; У. С. Шиев (1999). Классическая релятивистская динамика многих тел. Springer. п. 99. ISBN  0-7923-5737-X.
12. Компанеец А.С. (2003). Теоретическая физика (Перепечатка 2-го изд. 1962 г.). Courier Dover Publications. п. 118. ISBN  0-486-49532-9.
13. М Средницкий (2007). Квантовая теория поля. Издательство Кембриджского университета. Глава 4. ISBN  978-0-521-86449-7.
14. Карло Ровелли (2004). Квантовая гравитация. Издательство Кембриджского университета. п. 98 сл. ISBN  0-521-83733-2.
15. Уильям Баркер; Роджер Хоу (2008). Непрерывная симметрия: от Евклида до Клейна. Американское математическое общество. п. 18 сл. ISBN  978-0-8218-3900-3.
16. Арлан Рамзи; Роберт Д. Рихтмайер (1995). Введение в гиперболическую геометрию. Springer. п.11. ISBN  0-387-94339-0. система координат аксиомы геометрии.
17. Согласно Хокингу и Эллису: «Многообразие - это пространство, локально похожее на евклидово пространство в том, что оно может быть покрыто координатными фрагментами. Эта структура позволяет определить дифференциацию, но не делает различий между различными системами координат. Таким образом, определены единственные концепции. структурой многообразия являются те, которые не зависят от выбора системы координат ». Стивен У. Хокинг; Джордж Фрэнсис Рейнер Эллис (1973). Крупномасштабная структура пространства-времени. Издательство Кембриджского университета. п. 11. ISBN  0-521-09906-4. Математическое определение: Связанный Пространство Хаусдорфа M называется п-мерное многообразие, если каждая точка M содержится в открытом множестве, гомеоморфном открытому множеству в евклидовом п-мерное пространство.
18. Шигеюки Морита; Теруко Нагасе; Кацуми Номидзу (2001). Геометрия дифференциальных форм. Книжный магазин Американского математического общества. п.12. ISBN  0-8218-1045-6. система координат аксиомы геометрии.
19. Гранино Артур Корн; Тереза ​​М. Корн (2000). Математический справочник для ученых и инженеров: определения, теоремы и формулы для справки и обзора. Courier Dover Publications. п. 169. ISBN  0-486-41147-8.
20. Видеть Encarta определение. В архиве 2009-10-31.
21. Кацу Яманэ (2004). Моделирование и создание движений человеческих фигур. Springer. С. 12–13. ISBN  3-540-20317-6.
22. Ахиллеус Папапетру (1974). Лекции по общей теории относительности. Springer. п. 5. ISBN  90-277-0540-2.
23. Уилфорд Здунковски; Андреас Ботт (2003). Динамика атмосферы. Издательство Кембриджского университета. п. 84. ISBN  0-521-00666-X.
24. Борисенко А.И. И. Е. Тарапов; Ричард А. Сильверман (1979). Векторный и тензорный анализ с приложениями. Courier Dover Publications. п. 86. ISBN  0-486-63833-2.
25. Видеть Арвинд Кумар; Шриш Барв (2003). Как и почему в базовой механике. Ориент Лонгман. п. 115. ISBN  81-7371-420-7.
26. Крис Доран; Энтони Ласенби (2003). Геометрическая алгебра для физиков. Издательство Кембриджского университета. п. §5.2.2, с. 133. ISBN  978-0-521-71595-9..
27. Например, Мёллер заявляет: «Очевидно, что вместо декартовых координат мы можем с таким же успехом использовать общие криволинейные координаты для фиксации точек в физическом пространстве… Теперь мы введем общие« криволинейные »координаты Икс^я в четырехместном пространстве… " К. Мёллер (1952). Теория относительности. Издательство Оксфордского университета. п. 222 и стр. 233.
28. А. П. Лайтман; W. H. Press; Р. Х. Прайс; Теукольский С.А. (1975). Сборник задач по теории относительности и гравитации. Издательство Принстонского университета. п.15. ISBN  0-691-08162-X. релятивистские общие координаты.
29. Ричард Л. Фабер (1983). Дифференциальная геометрия и теория относительности: введение. CRC Press. п. 211. ISBN  0-8247-1749-X.
30. Ричард Вольфсон (2003). Просто Эйнштейн. W W Norton & Co. стр. 216. ISBN  0-393-05154-4.
31. Видеть Гвидо Рицци; Маттео Лука Руджеро (2003). Относительность во вращающихся системах отсчета. Springer. п. 33. ISBN  1-4020-1805-3..
32. То есть оба описания эквивалентны и могут использоваться по мере необходимости. Эта эквивалентность не выполняется вне общей теории относительности, например, в энтропийная гравитация.