Обобщенные координаты - Generalized coordinates

В аналитическая механика, период, термин обобщенные координаты относится к параметрам, которые описывают конфигурация из система относительно некоторой эталонной конфигурации. Эти параметры должны однозначно определять конфигурацию системы относительно эталонной конфигурации.^[1] Это делается при условии, что это можно сделать с помощью одного диаграмма. В обобщенные скорости время производные обобщенных координат системы.

Примером обобщенной координаты является угол, определяющий положение точки, движущейся по окружности. Прилагательное «обобщенный» отличает эти параметры от традиционного использования термина «координата» для обозначения Декартовы координаты: например, описание положения точки на окружности с использованием координат x и y.

Хотя может быть много вариантов обобщенных координат для физической системы, параметры, которые удобны, обычно выбираются для спецификации конфигурации системы и которые позволяют решить ее. уравнения движения Полегче. Если эти параметры не зависят друг от друга, количество независимых обобщенных координат определяется количеством степени свободы системы.^[2][3]

Обобщенные координаты сочетаются с обобщенными импульсами, чтобы обеспечить канонические координаты на фазовое пространство.

Ограничения и степени свободы

Открытый прямой путь

Открытый изогнутый путь F(Икс, у) = 0

Замкнутый изогнутый путь C(Икс, у) = 0

Одна обобщенная координата (одна степень свободы) на путях в 2D. Только одна обобщенная координата необходима, чтобы однозначно указать положения на кривой. В этих примерах этой переменной является длина дуги. s или угол θ. Имея обе декартовы координаты (Икс, у) не нужны, поскольку либо Икс или у связана с другим уравнениями кривых. Они также могут быть параметризованы s или θ.

Открытый изогнутый путь F(Икс, у) = 0. Множественные пересечения радиуса с путем.

Замкнутый изогнутый путь C(Икс, у) = 0. Самопересечение пути.

Длина дуги s вдоль кривой является допустимой обобщенной координатой, поскольку положение определяется однозначно, но угол θ нет, так как для одного значения θ.

Обобщенные координаты обычно выбираются так, чтобы обеспечить минимальное количество независимых координат, которые определяют конфигурацию системы, что упрощает формулировку Уравнения Лагранжа движения. Однако может также случиться, что полезный набор обобщенных координат может быть зависимый, что означает, что они связаны одним или несколькими ограничение уравнения.

Голономные ограничения

Открытая криволинейная поверхность F(Икс, у, z) = 0

Закрытая криволинейная поверхность S(Икс, у, z) = 0

Две обобщенные координаты, две степени свободы на криволинейных поверхностях в 3D. Всего два числа (ты, v) необходимы для указания точек на кривой, для каждого случая показана одна возможность. Полные три Декартовы координаты (Икс, у, z) не нужны, потому что любые два определяют третье согласно уравнениям кривых.

Для системы N частицы в 3D реальное координатное пространство, то вектор положения каждой частицы можно записать как 3-кортеж в Декартовы координаты:

${\displaystyle \mathbf {r} _{1}=(x_{1},y_{1},z_{1})\,,\quad \mathbf {r} _{2}=(x_{2},y_{2},z_{2})\,,\ldots \,,\mathbf {r} _{N}=(x_{N},y_{N},z_{N})\,.}$

Любой из векторов положения можно обозначить р_k где k = 1, 2, ..., N маркирует частицы. А голономная связь это уравнение связи формы для частицы k^{[4][nb 1]}

${\displaystyle f(\mathbf {r} _{k},t)=0}$

который соединяет вместе все 3 пространственные координаты этой частицы, поэтому они не являются независимыми. Ограничение может измениться со временем, поэтому время т явным образом появится в уравнениях связей. В любой момент времени любая одна координата будет определяться из других координат, например если Икс_k и z_k даны, значит, так у_k. Одно уравнение связи считается как один ограничение. Если есть C ограничений, у каждого есть уравнение, поэтому будет C уравнения связей. Необязательно существует одно уравнение связи для каждой частицы, и если в системе нет ограничений, то уравнения связи отсутствуют.

Пока конфигурация системы определяется 3N количества, но C координаты могут быть исключены, по одной координате из каждого уравнения ограничения. Количество независимых координат п = 3N − C. (В D размеры, в исходной конфигурации потребуется ND координаты, а редукция ограничениями означает п = ND − C). Идеально использовать минимальное количество координат, необходимое для определения конфигурации всей системы, при этом пользуясь ограничениями системы. Эти величины известны как обобщенные координаты в этом контексте обозначается q_j(т). Их удобно собирать в п-кортеж

${\displaystyle \mathbf {q} (t)=(q_{1}(t),q_{2}(t),\ldots ,q_{n}(t))}$

что является точкой в конфигурационное пространство системы. Все они независимы друг от друга и зависят от времени. Геометрически они могут быть отрезками по прямым линиям или длина дуги по кривым или углам; не обязательно декартовы координаты или другие стандартные ортогональные координаты. По одному на каждый степень свободы, поэтому количество обобщенных координат равно количеству степеней свободы, п. Степень свободы соответствует одной величине, которая изменяет конфигурацию системы, например, углу маятника или длине дуги, которую проходит валик вдоль проволоки.

Если можно найти из ограничений столько независимых переменных, сколько существует степеней свободы, их можно использовать как обобщенные координаты.^[5] Вектор положения р_k частицы k является функцией всех п обобщенные координаты (а через них и время),^{[6][7][8][5][nb 2]}

${\displaystyle \mathbf {r} _{k}=\mathbf {r} _{k}(\mathbf {q} (t))\,,}$

а обобщенные координаты можно рассматривать как параметры, связанные с ограничением.

Соответствующие производные по времени от q являются обобщенные скорости,

${\displaystyle {\dot {\mathbf {q} }}={\frac {d\mathbf {q} }{dt}}=({\dot {q}}_{1}(t),{\dot {q}}_{2}(t),\ldots ,{\dot {q}}_{n}(t))}$

(каждая точка над количеством означает один производная по времени ). Вектор скорости v_k это полная производная из р_k относительно времени

${\displaystyle \mathbf {v} _{k}={\dot {\mathbf {r} }}_{k}={\frac {d\mathbf {r} _{k}}{dt}}=\sum _{j=1}^{n}{\frac {\partial \mathbf {r} _{k}}{\partial q_{j}}}{\dot {q}}_{j}\,.}$

и поэтому обычно зависит от обобщенных скоростей и координат. Поскольку мы можем задавать начальные значения обобщенных координат и скоростей отдельно, обобщенные координаты q_j и скорости dq_j/dt можно рассматривать как независимые переменные.

Неголономные ограничения

Механическая система может включать ограничения как на обобщенные координаты, так и на их производные. Ограничения этого типа известны как неголономные. Неголономные связи первого порядка имеют вид

${\displaystyle g(\mathbf {q} ,{\dot {\mathbf {q} }},t)=0\,,}$

Примером такого ограничения является вращающееся колесо или острие, ограничивающее направление вектора скорости. Неголономные ограничения могут также включать производные следующего порядка, такие как обобщенные ускорения.

Физические величины в обобщенных координатах

Кинетическая энергия

Общая кинетическая энергия системы - это энергия движения системы, определяемая как^[9]

${\displaystyle T={\frac {1}{2}}\sum _{k=1}^{N}m_{k}{\dot {\mathbf {r} }}_{k}\cdot {\dot {\mathbf {r} }}_{k}\,,}$

в котором · является скалярное произведение. Кинетическая энергия зависит только от скоростей v_kа не координаты р_k самих себя. Напротив, важное наблюдение^[10]

${\displaystyle {\dot {\mathbf {r} }}_{k}\cdot {\dot {\mathbf {r} }}_{k}=\sum _{i,j=1}^{n}\left({\frac {\partial \mathbf {r} _{k}}{\partial q_{i}}}\cdot {\frac {\partial \mathbf {r} _{k}}{\partial q_{j}}}\right){\dot {q}}_{i}{\dot {q}}_{j},}$

который показывает, что кинетическая энергия, как правило, является функцией обобщенных скоростей, координат и времени, если ограничения также меняются со временем, поэтому Т = Т(q, dq/dt, т).

В случае, если ограничения на частицы не зависят от времени, тогда все частные производные по времени равны нулю, а кинетическая энергия равна однородная функция степени 2 по обобщенным скоростям.

Тем не менее для случая, не зависящего от времени, это выражение эквивалентно взятию линейный элемент квадрат траектории частицы k,

${\displaystyle ds_{k}^{2}=d\mathbf {r} _{k}\cdot d\mathbf {r} _{k}=\sum _{i,j=1}^{n}\left({\frac {\partial \mathbf {r} _{k}}{\partial q_{i}}}\cdot {\frac {\partial \mathbf {r} _{k}}{\partial q_{j}}}\right)dq_{i}dq_{j}\,,}$

и разделив на квадратный дифференциал по времени, dt², чтобы получить квадрат скорости частицы k. Таким образом, для не зависящих от времени ограничений достаточно знать линейный элемент, чтобы быстро получить кинетическую энергию частиц и, следовательно, лагранжиан.^[11]

Поучительно увидеть различные случаи полярных координат в 2d и 3d из-за их частого появления. Через 2 дня полярные координаты (р, θ),

${\displaystyle \left({\frac {ds}{dt}}\right)^{2}={\dot {r}}^{2}+r^{2}{\dot {\theta }}^{2}\,,}$

в 3D цилиндрические координаты (р, θ, z),

${\displaystyle \left({\frac {ds}{dt}}\right)^{2}={\dot {r}}^{2}+r^{2}{\dot {\theta }}^{2}+{\dot {z}}^{2}\,,}$

в 3D сферические координаты (р, θ, φ),

${\displaystyle \left({\frac {ds}{dt}}\right)^{2}={\dot {r}}^{2}+r^{2}{\dot {\theta }}^{2}+r^{2}\sin ^{2}\theta \,{\dot {\varphi }}^{2}\,.}$

Обобщенный импульс

В обобщенный импульс "канонически сопряженный к "координате q_я определяется

${\displaystyle p_{i}={\frac {\partial L}{\partial {\dot {q}}_{i}}}.}$

Если лагранжиан L делает нет зависит от некоторой координаты q_я, то из уравнений Эйлера – Лагранжа следует, что соответствующий обобщенный импульс будет сохраненное количество, поскольку производная по времени равна нулю, это означает, что импульс является константой движения;

${\displaystyle {\dot {p}}_{i}={\frac {d}{dt}}{\frac {\partial L}{\partial {\dot {q}}_{i}}}={\frac {\partial L}{\partial q_{i}}}=0\,.}$

Примеры

Бусина на проволоке

Бусинка вынуждена двигаться по проводу без трения. Проволока проявляет силу реакции C на бусине, чтобы она оставалась на проволоке. Неограничивающая сила N в данном случае - гравитация. Обратите внимание, что исходное положение провода может привести к различным движениям.

Для борта, скользящего по проволоке без трения, действующей только под действием силы тяжести в 2-м пространстве, ограничение на бусину можно сформулировать в виде ж(р) = 0, где положение бусинки можно записать р = (Икс(s), у(s)), в котором s параметр, длина дуги s по кривой от некоторой точки на проводе. Это подходящий выбор обобщенной координаты для системы. Только один координата нужна вместо двух, потому что положение борта может быть параметризовано одним числом, s, а уравнение связи связывает две координаты Икс и у; одно определяется из другого. Сила ограничения - это сила реакции, которую проволока оказывает на борт, чтобы удерживать ее на проволоке, а приложенная сила без ограничения - это сила тяжести, действующая на борт.

Предположим, что проволока со временем меняет свою форму, изгибаясь. Тогда уравнение связи и положение частицы соответственно

${\displaystyle f(\mathbf {r} ,t)=0\,,\quad \mathbf {r} =(x(s,t),y(s,t))}$

которые теперь оба зависят от времени т из-за изменения координат, когда проволока меняет свою форму. Время уведомления отображается неявно через координаты и явно в уравнениях связи.

Простой маятник

Простой маятник. Поскольку шток жесткий, положение боба ограничено уравнением ж(Икс, у) = 0, сила связи C это натяжение стержня. Опять не сдерживающая сила N в данном случае - гравитация.

Динамическая модель простого маятника.

Связь между использованием обобщенных координат и декартовых координат для характеристики движения механической системы можно проиллюстрировать, рассмотрев ограниченную динамику простого маятника.^[12][13]

Простой маятник состоит из массы M, свисающей с точки поворота, так что она вынуждена двигаться по окружности радиуса L. Положение массы определяется вектором координат р= (x, y) измеряется в плоскости круга так, что y находится в вертикальном направлении. Координаты x и y связаны уравнением окружности

${\displaystyle f(x,y)=x^{2}+y^{2}-L^{2}=0,}$

который ограничивает движение M. Это уравнение также обеспечивает ограничение на компоненты скорости,

${\displaystyle {\dot {f}}(x,y)=2x{\dot {x}}+2y{\dot {y}}=0.}$

Теперь введем параметр θ, который определяет угловое положение M относительно вертикального направления. Его можно использовать для определения координат x и y, так что

${\displaystyle \mathbf {r} =(x,y)=(L\sin \theta ,-L\cos \theta ).}$

Использование θ для определения конфигурации этой системы позволяет избежать ограничения, обеспечиваемого уравнением окружности.

Обратите внимание, что сила тяжести, действующая на массу m, формулируется в обычных декартовых координатах:

${\displaystyle \mathbf {F} =(0,-mg),}$

где g - ускорение свободного падения.

В виртуальная работа силы тяжести на массу m по траектории р дан кем-то

${\displaystyle \delta W=\mathbf {F} \cdot \delta \mathbf {r} .}$

Вариация ${\displaystyle \delta }$р может быть вычислено в терминах координат x и y или в терминах параметра θ,

${\displaystyle \delta \mathbf {r} =(\delta x,\delta y)=(L\cos \theta ,L\sin \theta )\delta \theta .}$

Таким образом, виртуальная работа задается

${\displaystyle \delta W=-mg\delta y=-mgL\sin \theta \delta \theta .}$

Обратите внимание, что коэффициент ${\displaystyle \delta }$y - y-составляющая приложенной силы. Таким же образом коэффициент ${\displaystyle \delta }$θ известен как обобщенная сила по обобщенной координате θ, задаваемой формулой

${\displaystyle F_{\theta }=-mgL\sin \theta .}$

Чтобы завершить анализ, рассмотрим кинетическую энергию T массы, используя скорость

${\displaystyle \mathbf {v} =({\dot {x}},{\dot {y}})=(L\cos \theta ,L\sin \theta ){\dot {\theta }},}$

так,

${\displaystyle T={\frac {1}{2}}m\mathbf {v} \cdot \mathbf {v} ={\frac {1}{2}}m({\dot {x}}^{2}+{\dot {y}}^{2})={\frac {1}{2}}mL^{2}{\dot {\theta }}^{2}.}$

Форма принципа виртуальной работы Даламбера для маятника в терминах координат x и y задаются формулами,

${\displaystyle {\frac {d}{dt}}{\frac {\partial T}{\partial {\dot {x}}}}-{\frac {\partial T}{\partial x}}=F_{x}+\lambda {\frac {\partial f}{\partial x}},\quad {\frac {d}{dt}}{\frac {\partial T}{\partial {\dot {y}}}}-{\frac {\partial T}{\partial y}}=F_{y}+\lambda {\frac {\partial f}{\partial y}}.}$

Это дает три уравнения

${\displaystyle m{\ddot {x}}=\lambda (2x),\quad m{\ddot {y}}=-mg+\lambda (2y),\quad x^{2}+y^{2}-L^{2}=0,}$

в трех неизвестных, x, y и λ.

Используя параметр θ, эти уравнения принимают вид

${\displaystyle {\frac {d}{dt}}{\frac {\partial T}{\partial {\dot {\theta }}}}-{\frac {\partial T}{\partial \theta }}=F_{\theta },}$

который становится,

${\displaystyle mL^{2}{\ddot {\theta }}=-mgL\sin \theta ,}$

или

${\displaystyle {\ddot {\theta }}+{\frac {g}{L}}\sin \theta =0.}$

Эта формулировка дает одно уравнение, потому что есть один параметр и нет уравнения ограничений.

Это показывает, что параметр θ является обобщенной координатой, которую можно использовать так же, как декартовы координаты x и y для анализа маятника.

Двойной маятник

А двойной маятник

Преимущества обобщенных координат становятся очевидными при анализе двойной маятник. Для двух масс масс_я, i = 1, 2, пусть р_я= (х_я, y_я), i = 1, 2, определяют две их траектории. Эти векторы удовлетворяют двум уравнениям связи:

${\displaystyle f_{1}(x_{1},y_{1},x_{2},y_{2})=\mathbf {r} _{1}\cdot \mathbf {r} _{1}-L_{1}^{2}=0}$

и

${\displaystyle f_{2}(x_{1},y_{1},x_{2},y_{2})=(\mathbf {r} _{2}-\mathbf {r} _{1})\cdot (\mathbf {r} _{2}-\mathbf {r} _{1})-L_{2}^{2}=0.}$

Формулировка уравнений Лагранжа для этой системы дает шесть уравнений в четырех декартовых координатах x_я, y_я i = 1, 2 и два множителя Лагранжа λ_я, i = 1, 2, которые возникают из двух уравнений связи.

Теперь введем обобщенные координаты θ_я i = 1,2, которые определяют угловое положение каждой массы двойного маятника от вертикального направления. В этом случае мы имеем

${\displaystyle \mathbf {r} _{1}=(L_{1}\sin \theta _{1},-L_{1}\cos \theta _{1}),\quad \mathbf {r} _{2}=(L_{1}\sin \theta _{1},-L_{1}\cos \theta _{1})+(L_{2}\sin \theta _{2},-L_{2}\cos \theta _{2}).}$

Сила тяжести, действующая на массы, определяется выражением

${\displaystyle \mathbf {F} _{1}=(0,-m_{1}g),\quad \mathbf {F} _{2}=(0,-m_{2}g)}$

где g - ускорение свободного падения. Следовательно, виртуальная работа гравитации над двумя массами, движущимися по траекториям р_я, i = 1,2 определяется выражением

${\displaystyle \delta W=\mathbf {F} _{1}\cdot \delta \mathbf {r} _{1}+\mathbf {F} _{2}\cdot \delta \mathbf {r} _{2}.}$

Вариации δр_я i = 1, 2 можно вычислить как

${\displaystyle \delta \mathbf {r} _{1}=(L_{1}\cos \theta _{1},L_{1}\sin \theta _{1})\delta \theta _{1},\quad \delta \mathbf {r} _{2}=(L_{1}\cos \theta _{1},L_{1}\sin \theta _{1})\delta \theta _{1}+(L_{2}\cos \theta _{2},L_{2}\sin \theta _{2})\delta \theta _{2}}$

Таким образом, виртуальная работа задается

${\displaystyle \delta W=-(m_{1}+m_{2})gL_{1}\sin \theta _{1}\delta \theta _{1}-m_{2}gL_{2}\sin \theta _{2}\delta \theta _{2},}$

а обобщенные силы равны

${\displaystyle F_{\theta _{1}}=-(m_{1}+m_{2})gL_{1}\sin \theta _{1},\quad F_{\theta _{2}}=-m_{2}gL_{2}\sin \theta _{2}.}$

Вычислите кинетическую энергию этой системы, чтобы она была

${\displaystyle T={\frac {1}{2}}m_{1}\mathbf {v} _{1}\cdot \mathbf {v} _{1}+{\frac {1}{2}}m_{2}\mathbf {v} _{2}\cdot \mathbf {v} _{2}={\frac {1}{2}}(m_{1}+m_{2})L_{1}^{2}{\dot {\theta }}_{1}^{2}+{\frac {1}{2}}m_{2}L_{2}^{2}{\dot {\theta }}_{2}^{2}+m_{2}L_{1}L_{2}\cos(\theta _{2}-\theta _{1}){\dot {\theta }}_{1}{\dot {\theta }}_{2}.}$

Уравнение Эйлера – Лагранжа. дают два уравнения в неизвестных обобщенных координатах θ_я i = 1, 2, задаваемый^[14]

${\displaystyle (m_{1}+m_{2})L_{1}^{2}{\ddot {\theta }}_{1}+m_{2}L_{1}L_{2}{\ddot {\theta }}_{2}\cos(\theta _{2}-\theta _{1})+m_{2}L_{1}L_{2}{\ddot {\theta _{2}}}^{2}\sin(\theta _{1}-\theta _{2})=-(m_{1}+m_{2})gL_{1}\sin \theta _{1},}$

и

${\displaystyle m_{2}L_{2}^{2}{\ddot {\theta }}_{2}+m_{2}L_{1}L_{2}{\ddot {\theta }}_{1}\cos(\theta _{2}-\theta _{1})+m_{2}L_{1}L_{2}{\ddot {\theta _{1}}}^{2}\sin(\theta _{2}-\theta _{1})=-m_{2}gL_{2}\sin \theta _{2}.}$

Использование обобщенных координат θ_я i = 1, 2 представляет собой альтернативу декартовой формулировке динамики двойного маятника.

Сферический маятник

Сферический маятник: углы и скорости.

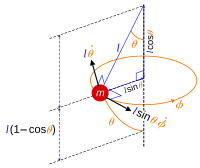
Для трехмерного примера сферический маятник с постоянной длиной л свободно качаться в любом угловом направлении под действием силы тяжести, ограничение на маятник может быть указано в виде

${\displaystyle f(\mathbf {r} )=x^{2}+y^{2}+z^{2}-l^{2}=0\,,}$

где положение маятника может быть записано

${\displaystyle \mathbf {r} =(x(\theta ,\phi ),y(\theta ,\phi ),z(\theta ,\phi ))\,,}$

в котором (θ, φ) являются сферические полярные углы потому что боб движется по поверхности сферы. Позиция р измеряется вдоль точки подвеса к бобу, здесь рассматривается как точечная частица. Логичным выбором обобщенных координат для описания движения являются углы (θ, φ). Требуются только две координаты вместо трех, потому что положение боба может быть параметризовано двумя числами, а уравнение ограничения связывает три координаты Икс, у, z поэтому любой из них определяется двумя другими.

Обобщенные координаты и виртуальная работа

В принцип виртуальной работы утверждает, что если система находится в статическом равновесии, виртуальная работа приложенных сил равна нулю для всех виртуальных перемещений системы из этого состояния, то есть ${\displaystyle \delta }$W = 0 для любого варианта ${\displaystyle \delta }$р.^[15] При формулировании в терминах обобщенных координат это эквивалентно требованию, чтобы обобщенные силы для любого виртуального смещения равнялись нулю, т. Е. F_я=0.

Пусть силы на систему равны F_j, j = 1, ..., м применяться к точкам с декартовыми координатами р_j, j = 1, ..., m, то виртуальная работа, создаваемая виртуальным смещением из положения равновесия, определяется выражением

${\displaystyle \delta W=\sum _{j=1}^{m}\mathbf {F} _{j}\cdot \delta \mathbf {r} _{j}.}$

где δр_j, j = 1, ..., м обозначают виртуальные перемещения каждой точки тела.

Теперь предположим, что каждое δр_j зависит от обобщенных координат q_я, я = 1, ..., п, тогда

${\displaystyle \delta \mathbf {r} _{j}={\frac {\partial \mathbf {r} _{j}}{\partial q_{1}}}\delta {q}_{1}+\ldots +{\frac {\partial \mathbf {r} _{j}}{\partial q_{n}}}\delta {q}_{n},}$

и

${\displaystyle \delta W=\left(\sum _{j=1}^{m}\mathbf {F} _{j}\cdot {\frac {\partial \mathbf {r} _{j}}{\partial q_{1}}}\right)\delta {q}_{1}+\ldots +\left(\sum _{j=1}^{m}\mathbf {F} _{j}\cdot {\frac {\partial \mathbf {r} _{j}}{\partial q_{n}}}\right)\delta {q}_{n}.}$

В п термины

${\displaystyle F_{i}=\sum _{j=1}^{m}\mathbf {F} _{j}\cdot {\frac {\partial \mathbf {r} _{j}}{\partial q_{i}}},\quad i=1,\ldots ,n,}$

- обобщенные силы, действующие на систему. Кейн^[16] показывает, что эти обобщенные силы также могут быть сформулированы в терминах отношения производных по времени,

${\displaystyle F_{i}=\sum _{j=1}^{m}\mathbf {F} _{j}\cdot {\frac {\partial \mathbf {v} _{j}}{\partial {\dot {q}}_{i}}},\quad i=1,\ldots ,n,}$

где v_j - скорость точки приложения силы F_j.

Чтобы виртуальная работа была равна нулю для произвольного виртуального смещения, каждая из обобщенных сил должна быть равна нулю, то есть

${\displaystyle \delta W=0\quad \Rightarrow \quad F_{i}=0,i=1,\ldots ,n.}$

Смотрите также

• Канонические координаты
• Гамильтонова механика
• Виртуальная работа
• Ортогональные координаты
• Криволинейные координаты
• Матрица масс
• Матрица жесткости
• Обобщенные силы

Примечания

1. Некоторые авторы устанавливают уравнения связей на постоянное значение для удобства с некоторыми уравнениями связей (например, с маятниками), другие устанавливают его на ноль. Это не имеет значения, потому что константа может быть вычтена, чтобы получить ноль на одной стороне уравнения. Кроме того, в уравнениях Лагранжа первого рода нужны только производные.
2. Некоторые авторы, например Рука и Зяблик принимают форму вектора положения частицы k, как показано здесь, как условие голономности этой частицы.

Рекомендации

1. Гинзберг 2008, п. 397, §7.2.1 Выбор обобщенных координат
2. Фарид М. Л. Амируш (2006). «§2.4: Обобщенные координаты». Основы многотельной динамики: теория и приложения. Springer. п. 46. ISBN  0-8176-4236-6.
3. Флориан Шек (2010). «§5.1 Многообразия обобщенных координат». Механика: от законов Ньютона к детерминированному хаосу (5-е изд.). Springer. п. 286. ISBN  978-3-642-05369-6.
4. Гольдштейн 1980, п. 12 ошибка harvnb: цель отсутствует: CITEREFGoldstein1980 (Помогите)
5. Киббл и Беркшир 2004, п. 232
6. Торби 1984, п. 260
7. Гольдштейн 1980, п. 13 ошибка harvnb: цель отсутствует: CITEREFGoldstein1980 (Помогите)
8. Рука и Финч 2008, п. 15 Ошибка harvnb: нет цели: CITEREFHandFinch2008 (Помогите)
9. Торби 1984, п. 269
10. Гольдштейн 1980, п. 25 ошибка harvnb: цель отсутствует: CITEREFGoldstein1980 (Помогите)
11. Ландау и Лифшиц, 1976 г., п. 8 Ошибка harvnb: цель отсутствует: CITEREFLandauLifshitz1976 (Помогите)
12. Гринвуд, Дональд Т. (1987). Принципы динамики (2-е изд.). Прентис Холл. ISBN  0-13-709981-9.
13. Ричард Фицпатрик, Newtonian Dynamics, http://farside.ph.utexas.edu/teaching/336k/Newton/Newtonhtml.html.
14. Эрик В. Вайсштейн, Двойной маятник, scienceworld.wolfram.com. 2007 г.
15. Торби, Брюс (1984). «Энергетические методы». Продвинутая динамика для инженеров. Серия HRW в машиностроении. Соединенные Штаты Америки: CBS College Publishing. ISBN  0-03-063366-4.
16. Т. Р. Кейн, Д. А. Левинсон, Динамика: теория и приложения, McGraw-Hill, Нью-Йорк, 1985.

Библиография цитируемых ссылок

• Гинзберг, Джерри Х. (2008). Инженерная динамика (3-е изд.). Кембридж, Великобритания: Издательство Кембриджского университета. ISBN  978-0-521-88303-0.
• Киббл, T.W.B; Беркшир, Ф.Х. (2004). Классическая механика (5-е изд.). Ривер Эдж, штат Нью-Джерси: Imperial College Press. ISBN  1860944248.