Вероятностная мера - Probability measure

Во многих случаях, статистическая физика использует вероятностные меры, но не все меры он использует вероятностные меры.^[1][2]

В математика, а вероятностная мера это функция с действительным знаком определяется набором событий в вероятностное пространство это удовлетворяет мера свойства, такие как счетная аддитивность.^[3] Разница между вероятностной мерой и более общим понятием меры (которое включает такие понятия, как площадь или же объем ) состоит в том, что вероятностная мера должна присвоить значение 1 всему вероятностному пространству.

Интуитивно свойство аддитивности говорит, что вероятность, присвоенная объединению двух непересекающихся событий мерой, должна быть суммой вероятностей событий, например значение, присвоенное «1 или 2» при броске кубика, должно быть суммой значений, присвоенных «1» и «2».

Вероятностные меры имеют приложения в самых разных областях, от физики до финансов и биологии.

Определение

А вероятностная мера отображение вероятностного пространства для ${\displaystyle 2^{3}}$ события в единичный интервал.

Требования к функции μ быть вероятностной мерой на вероятностное пространство это что:

• μ должен возвращать результаты в единичный интервал [0, 1], возвращая 0 для пустого набора и 1 для всего пространства.

• μ должен удовлетворить счетная аддитивность собственность, которая для всех счетный коллекции ${\displaystyle \{E_{i}\}}$ попарно непересекающиеся множества:

${\displaystyle \mu {\Bigl (}\bigcup _{i\in I}E_{i}{\Bigr )}=\sum _{i\in I}\mu (E_{i}).}$

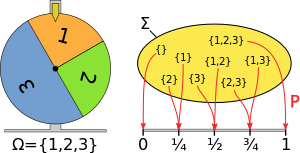
Например, учитывая три элемента 1, 2 и 3 с вероятностями 1/4, 1/4 и 1/2, значение, присвоенное {1, 3}, равно 1/4 + 1/2 = 3/4, как в диаграмма справа.

В условная возможность на основе пересечения событий, определенных как:

${\displaystyle \mu (B\mid A)={\frac {\mu (A\cap B)}{\mu (A)}}.}$

удовлетворяет требованиям вероятностной меры, пока ${\displaystyle \mu (A)}$ не равно нулю.^[4]

Вероятностные меры отличаются от более общего понятия нечеткие меры в котором не требуется, чтобы сумма нечетких значений равнялась 1, а аддитивное свойство заменено отношением порядка, основанным на установить включение.

Примеры приложений

Рыночные меры которые приписывают вероятности финансовый рынок пространства, основанные на реальных движениях рынка, являются примерами вероятностных мер, которые представляют интерес для математические финансы, например в ценообразовании финансовые производные.^[5] Например, нейтральная к риску мера является вероятностной мерой, предполагающей, что текущая стоимость активов является ожидаемое значение будущей выплаты, взятой в отношении той же нейтральной к риску меры (т.е. рассчитанной с использованием соответствующей функции плотности нейтральной к риску), и со скидкой на безрисковая ставка. Если существует уникальная вероятностная мера, которая должна использоваться для определения цены активов на рынке, то рынок называется полный рынок.^[6]

Не все меры, которые интуитивно представляют шанс или вероятность, являются вероятностными. Например, хотя фундаментальная концепция системы в статистическая механика является мерным пространством, такие меры не всегда являются вероятностными.^[1] В общем, в статистической физике, если мы рассматриваем предложения вида «вероятность того, что система S принимает состояние A, является p», геометрия системы не всегда приводит к определению вероятностной меры при совпадении, хотя это возможно в случае систем с одной степенью свободы.^[2]

Вероятностные меры также используются в математическая биология.^[7] Например, в сравнительном анализ последовательности мера вероятности может быть определена для вероятности того, что вариант может быть допустимым для аминокислота в последовательности.^[8]

Ультрафильтры можно понимать как ${\displaystyle \{0,1\}}$-значные вероятностные меры, допускающие множество интуитивных доказательств, основанных на мерах. Например, Теорема Хиндмана может быть доказано дальнейшим исследованием этих мер, и их свертка особенно.

Смотрите также

• Мера Бореля
• Нечеткая мера
• Мера Хаара
• Мера мартингейла
• Мера Лебега

Рекомендации

1. Курс математики для студентов-физиков, Том 2 Пол Бамберг, Шломо Штернберг 1991 ISBN  0-521-40650-1 стр. 802
2. Понятие вероятности в статистической физике Яир М. Гуттманн, 1999 г. ISBN  0-521-62128-3 стр. 149
3. Введение в теоретико-мерную вероятность Джордж Г. Руссас, 2004 г. ISBN  0-12-599022-7 стр. 47
4. Вероятность, случайные процессы и эргодические свойства. Роберт М. Грей 2009 ISBN  1-4419-1089-1 стр.163
5. Количественные методы ценообразования деривативов Доминго Тавелла 2002 ISBN  0-471-39447-5 стр.11
6. Необратимые решения в условиях неопределенности Светлана Ивановна Боярченко, Серж Левендорскийĭ 2007 ISBN  3-540-73745-6 стр.11
7. Математические методы в биологии Дж. Дэвид Логан, Уильям Р. Волесенский, 2009 г. ISBN  0-470-52587-8 стр.195
8. Открытие биомолекулярных механизмов с помощью вычислительной биологии Фрэнк Эйзенхабер, 2006 г. ISBN  0-387-34527-2 стр.127

дальнейшее чтение

• Биллингсли, Патрик (1995). Вероятность и мера. Джон Вили. ISBN  0-471-00710-2.
• Эш, Роберт Б .; Doléans-Dade, Кэтрин А. (1999). Теория вероятностей и меры. Академическая пресса. ISBN  0-12-065202-1.

внешняя ссылка

• СМИ, связанные с Вероятностная мера в Wikimedia Commons