Введение в квантовую механику - Introduction to quantum mechanics

Квантовая механика это наука о очень маленьких вещах. Это объясняет поведение дело и его взаимодействие с энергия на масштаб из атомный и субатомные частицы. Напротив, классическая физика объясняет материю и энергию только в масштабе, знакомом человеческому опыту, включая поведение астрономических тел, таких как Луна. Классическая физика до сих пор используется в большей части современной науки и техники. Однако ближе к концу XIX века ученые обнаружили явления как в больших (макрос ) и малый (микро ) миры, которые классическая физика не могла объяснить.^[1] Стремление разрешить несоответствия между наблюдаемыми явлениями и классической теорией привело к двум крупным революциям в физике, которые изменили исходную научную парадигму: теория относительности и развитие квантовая механика.^[2] В этой статье описывается, как физики открыли ограничения классической физики и разработали основные концепции квантовой теории, пришедшие на смену ей в первые десятилетия 20-го века. Он описывает эти концепции примерно в том порядке, в котором они были впервые обнаружены. Для более полной истории вопроса см. История квантовой механики.

В некоторых аспектах свет ведет себя как частицы, а в других - как волны. Материя - «вещество» Вселенной, состоящее из таких частиц, как электроны и атомы - экспонаты волнообразное поведение тоже. Некоторые источники света, такие как неоновые лампы, излучают только определенные частоты света, небольшой набор различных чистых цветов, определяемых атомной структурой неона. Квантовая механика показывает, что свет, наряду со всеми другими формами электромагнитное излучение, поставляется в дискретных единицах, называемых фотоны, и предсказывает его спектральный энергии (соответствующие чистым цветам) и интенсивности его световых лучей. Одиночный фотон - это квант или наименьшая наблюдаемая частица электромагнитного поля. Частичный фотон экспериментально никогда не наблюдается. В более широком смысле квантовая механика показывает, что многие свойства объектов, такие как положение, скорость и угловой момент, которые казались непрерывными в уменьшенном масштабе классической механики, оказываются (в очень крошечной, увеличенной шкале квантовой механики) квантованный. Такие свойства элементарные частицы должны принимать одно из набора небольших дискретных допустимых значений, и поскольку разрыв между этими значениями также невелик, неоднородности проявляются только в очень крошечных (атомарных) масштабах.

Многие аспекты квантовой механики противоречат здравому смыслу.^[3] и может показаться парадоксальный потому что они описывают поведение, совершенно отличное от того, что наблюдается в более крупных масштабах. По словам квантового физика Ричард Фейнман, квантовая механика имеет дело с «природой такой, какая она есть - абсурдной».^[4]

Например, принцип неопределенности квантовой механики означает, что чем ближе один измерение (например, положение частицы), тем менее точным является другой дополнительный измерение, относящееся к одной и той же частице (например, ее скорость ) должен стать.

Другой пример запутанность, в котором измерение любого двузначного состояния частицы (например, света поляризованный вверх или вниз), выполненное на любой из двух «запутанных» частиц, которые очень далеко друг от друга, приводит к тому, что последующее измерение на другой частице всегда будет другим из двух значений (например, поляризованным в противоположном направлении).

Последний пример: сверхтекучесть, в котором емкость с жидким гелием, охлажденная почти до полный ноль при температуре самопроизвольно (медленно) течет вверх и над отверстием своего сосуда против силы тяжести.

Первая квантовая теория: Макс Планк и излучение черного тела

Горячие металлоконструкции. Желто-оранжевое свечение - это видимая часть теплового излучения, испускаемого из-за высокой температуры. Все остальное на картинке также светится тепловым излучением, но менее ярко и на более длинных волнах, чем может обнаружить человеческий глаз. Это излучение может наблюдать камера дальнего инфракрасного диапазона.

Тепловое излучение электромагнитное излучение, исходящее от поверхности объекта за счет внутренней энергии объекта. Если объект достаточно нагреть, он начинает излучать свет на красном конце спектр, как это становится красный горячий.

Его нагревание приводит к изменению цвета с красного на желтый, белый и синий, поскольку он излучает свет с более короткими длинами волн (более высокими частотами). Идеальный излучатель также является идеальным поглотителем: в холодную погоду такой объект выглядит совершенно черным, потому что он поглощает весь падающий на него свет и не излучает его. Следовательно, идеальный тепловой излучатель известен как черное тело, а испускаемое им излучение называется излучение черного тела.

Прогнозы количества теплового излучения различной частоты, испускаемого телом. Правильные значения, предсказанные законом Планка (зеленый), контрастируют с классическими значениями Закон Рэлея-Джинса (красный) и Вина приближение (синий).

В конце 19 века тепловое излучение было довольно хорошо охарактеризовано экспериментально.^{[примечание 1]} Однако классическая физика привела к Закон Рэлея – Джинса, что, как показано на рисунке, хорошо согласуется с экспериментальными результатами на низких частотах, но сильно не согласуется с высокими частотами. Физики искали единую теорию, объясняющую все экспериментальные результаты.

Первая модель, которая смогла объяснить полный спектр теплового излучения, была предложена Макс Планк в 1900 г.^[5] Он предложил математическую модель, в которой тепловое излучение находилось в равновесии с набором гармонические осцилляторы. Чтобы воспроизвести экспериментальные результаты, он должен был предположить, что каждый осциллятор излучает целое число единиц энергии на своей единственной характеристической частоте, а не может излучать любое произвольное количество энергии. Другими словами, энергия, излучаемая осциллятором, была квантованный.^{[заметка 2]} В квант согласно Планку, энергия каждого осциллятора была пропорциональна частоте осциллятора; константа пропорциональности теперь известна как Постоянная Планка. Постоянная Планка, обычно записываемая как $час$ , имеет значение 6.63×10⁻³⁴ J s. Итак, энергия $E$ генератора частоты $ж$ дан кем-то

{ displaystyle E = nhf, quad { text {where}} quad n = 1,2,3, ldots}

^[6]

Чтобы изменить цвет такого излучающего тела, необходимо изменить его температуру. Закон планка объясняет, почему: повышение температуры тела позволяет ему излучать больше энергии в целом и означает, что большая часть энергии направляется к фиолетовому концу спектра.

Закон планка была первой квантовой теорией в физике, и в 1918 году Планк получил Нобелевскую премию «в знак признания заслуг, которые он оказал развитию физики своим открытием квантов энергии».^[7] Однако в то время Планк считал квантование чисто эвристической математической конструкцией, а не (как сейчас считается) фундаментальным изменением в нашем понимании мира.^[8]

Фотоны: квантование света

Альберт Эйнштейн c. 1905

В 1905 г. Альберт Эйнштейн сделал дополнительный шаг. Он предположил, что квантование было не просто математической конструкцией, но что энергия в луче света фактически возникает в отдельных пакетах, которые теперь называются фотоны.^[9] Энергия одиночного фотона света частоты ${ displaystyle f}$ дается умножением частоты на постоянную Планка ${ displaystyle h}$ (очень маленькое положительное число):

{ displaystyle E = hf}

На протяжении веков ученые обсуждали две возможные теории света: волна или вместо этого поток крошечных частиц ? К 19-му веку в целом считалось, что дебаты разрешились в пользу волновой теории, поскольку она могла объяснить наблюдаемые эффекты, такие как преломление, дифракция, вмешательство, и поляризация.^[10] Джеймс Клерк Максвелл показали, что электричество, магнетизм и свет являются проявлениями одного и того же явления: электромагнитное поле. Уравнения Максвелла, которые представляют собой полный набор законов классический электромагнетизм, описывают свет как волны: комбинацию колеблющихся электрических и магнитных полей. Из-за преобладания доказательств в пользу волновой теории идеи Эйнштейна поначалу были встречены с большим скептицизмом. В конце концов, однако, предпочтение стало отдавать фотонной модели. Одним из наиболее важных доказательств в пользу этого метода была его способность объяснить несколько загадочных свойств фотоэлектрический эффект, описанный в следующем разделе. Тем не менее аналогия с волной оставалась незаменимой для понимания других характеристик света: дифракция, преломление, и вмешательство.

Фотоэлектрический эффект

Свет падает на поверхность слева. Если частота света достаточно высока, то есть если он обеспечивает достаточную энергию, отрицательно заряженные электроны выбрасываются из металла.

В 1887 г. Генрих Герц заметил, что когда свет с достаточной частотой попадает на металлическую поверхность, поверхность испускает электроны.^[11] В 1902 г. Филипп Ленард обнаружил, что максимально возможная энергия выброшенного электрона связана с частота света, а не его интенсивность: если частота слишком низкая, электроны не выбрасываются независимо от интенсивности. Сильные лучи света по направлению к красному концу спектра могут вообще не создавать электрического потенциала, в то время как слабые лучи света по направлению к фиолетовому концу спектра будут производить все более и более высокие напряжения. Самая низкая частота света, которая может вызвать испускание электронов, называемая пороговой частотой, различается для разных металлов. Это наблюдение противоречит классическому электромагнетизму, согласно которому энергия электрона должна быть пропорциональна интенсивности падающего излучения.^[12]^:24 Поэтому, когда физики впервые обнаружили устройства, демонстрирующие фотоэлектрический эффект, они изначально ожидали, что более высокая интенсивность света приведет к более высокому напряжению от фотоэлектрического устройства.

Эйнштейн объяснил эффект, постулировав, что луч света - это поток частиц ("фотоны ") и что, если луч имеет частоту $ж$ , то каждый фотон имеет энергию, равную $hf$ .^[11] Электрон, вероятно, будет поражен только одним фотоном, который передает не более энергии $hf$ к электрону.^[11] Следовательно, интенсивность луча не влияет^{[заметка 3]} и только его частота определяет максимальную энергию, которая может быть передана электрону.^[11]

Чтобы объяснить пороговый эффект, Эйнштейн утверждал, что для этого требуется определенное количество энергии, называемое рабочая функция и обозначается $φ$ , чтобы удалить электрон из металла.^[11] Это количество энергии разное для каждого металла. Если энергия фотона меньше работы выхода, то он не несет достаточной энергии для удаления электрона из металла. Пороговая частота, $ж 0$ , - частота фотона, энергия которого равна работе выхода:

{ displaystyle varphi = hf_ {0}.}

Если $ж$ больше, чем $ж 0$ , энергия $hf$ достаточно, чтобы удалить электрон. Выброшенный электрон имеет кинетическая энергия, $E K$ , которая в лучшем случае равна энергии фотона за вычетом энергии, необходимой для вытеснения электрона из металла:

{ displaystyle E_ {K} = hf- varphi = h (f-f_ {0}).}

Описание Эйнштейном света как состоящего из частиц расширило планковское понятие квантованной энергии, которое состоит в том, что один фотон заданной частоты, $ж$ доставляет неизменное количество энергии, $hf$ . Другими словами, отдельные фотоны могут отдавать больше или меньше энергии, но только в зависимости от их частот. В природе одиночные фотоны встречаются редко. Солнце и источники излучения, доступные в XIX веке, каждую секунду излучают огромное количество фотонов, поэтому важность энергии, переносимой каждым отдельным фотоном, не была очевидной. Идея Эйнштейна о том, что энергия, содержащаяся в отдельных единицах света, зависит от их частоты, позволила объяснить экспериментальные результаты, которые казались нелогичными. Однако, хотя фотон и является частицей, он все еще описывался как обладающий волнообразным свойством частоты. По сути, учет света как частицы недостаточен, и его волнообразный характер все еще требуется.^[13]^{[примечание 4]}

Последствия квантования света

Связь между частотой электромагнитного излучения и энергией каждого отдельного фотона - вот почему ультрафиолетовый свет может вызвать солнечный ожог, но видимый или инфракрасный свет не может. Фотон ультрафиолетового света доставляет большое количество энергия - достаточно, чтобы способствовать повреждению клеток, например, при солнечном ожоге. Фотон инфракрасного света дает меньше энергии - ее достаточно, чтобы согреть кожу. Таким образом, инфракрасная лампа может согреть большую поверхность, возможно, достаточно большую, чтобы людям было комфортно в холодной комнате, но она не может вызвать солнечный ожог.^[15]

Все фотоны одной частоты имеют одинаковую энергию, а все фотоны разных частот пропорционально (порядок 1, $E фотон = hf$ ) разные энергии.^[16] Однако, хотя энергия, передаваемая фотонами, неизменна на любой заданной частоте, начальное энергетическое состояние электронов в фотоэлектрическом устройстве до поглощения света не обязательно является однородным. В случае отдельных электронов могут иметь место аномальные результаты. Например, электрон, который уже был возбужден выше равновесного уровня фотоэлектрического устройства, может быть выброшен, когда он поглощает нехарактерно низкочастотное излучение. Однако статистически характерное поведение фотоэлектрического устройства отражает поведение подавляющего большинства его электронов, которые находятся на своем равновесном уровне. Этот момент помогает понять разницу между изучением отдельных частиц в квантовой динамике и изучением массивных частиц в классической физике.^{[нужна цитата ]}

Квантование материи: модель атома Бора

К началу 20-го века для доказательства потребовалась модель атома с диффузным облаком отрицательно заряженных электроны окружающий небольшой, плотный, положительно заряженный ядро. Эти свойства предложили модель, в которой электроны вращаются вокруг ядра, как планеты, вращающиеся вокруг Солнца.^{[примечание 5]} Однако было также известно, что атом в этой модели будет нестабильным: согласно классической теории, вращающиеся электроны испытывают центростремительное ускорение и, следовательно, должны испускать электромагнитное излучение, потеря энергии также заставляет их вращаться по спирали к ядру, сталкиваясь с ним. с ним за доли секунды.

Второй связанной загадкой была спектр излучения атомов. Когда газ нагревается, он излучает свет только на дискретных частотах. Например, видимый свет, излучаемый водород состоит из четырех разных цветов, как показано на рисунке ниже. Интенсивность света на разных частотах тоже разная. Напротив, белый свет представляет собой непрерывное излучение во всем диапазоне видимых частот. К концу девятнадцатого века простое правило, известное как Формула Бальмера показали, как частоты разных линий связаны друг с другом, хотя без объяснения причин и без каких-либо прогнозов относительно интенсивностей. Формула также предсказала некоторые дополнительные спектральные линии в ультрафиолетовом и инфракрасном свете, которые в то время не наблюдались. Эти линии позже наблюдались экспериментально, что повысило уверенность в ценности формулы.

Спектр излучения из водород. При возбуждении газообразный водород испускает свет четырех различных цветов (спектральных линий) в видимой области спектра, а также ряд линий в инфракрасной и ультрафиолетовой областях.

Математическая формула, описывающая спектр излучения водорода

В 1885 году швейцарский математик Иоганн Балмер обнаружил, что каждая длина волны $λ$ (лямбда) в видимом спектре водорода связана с некоторым целым числом $п$ по уравнению

{ displaystyle lambda = B left ({ frac {n ^ {2}} {n ^ {2} -4}} right) qquad qquad n = 3,4,5,6}

где $B$ постоянная Бальмера, определенная равной 364,56 нм.

В 1888 г. Йоханнес Ридберг обобщил и значительно увеличил объяснительную полезность формулы Бальмера. Он предсказал, что $λ$ связано с двумя целыми числами $п$ и $м$ согласно тому, что сейчас известно как Формула Ридберга:^[17]

{ displaystyle { frac {1} { lambda}} = R left ({ frac {1} {m ^ {2}}} - { frac {1} {n ^ {2}}} right ),}

где р это Постоянная Ридберга, равная 0,0110 нм⁻¹, и п должно быть больше чем м.

Формула Ридберга учитывает четыре видимые длины волн водорода, задавая $м = 2$ и $п = 3, 4, 5, 6$ . Он также предсказывает дополнительные длины волн в спектре излучения: для $м = 1$ и для $п > 1$ спектр излучения должен содержать определенные длины волн ультрафиолета, а для $м = 3$ и $п > 3$ , он также должен содержать определенные длины волн инфракрасного излучения. Экспериментальное наблюдение этих длин волн произошло два десятилетия спустя: в 1908 году. Луи Пашен нашел некоторые из предсказанных длин волн инфракрасного излучения, а в 1914 г. Теодор Лайман нашли некоторые из предсказанных длин волн ультрафиолета.^[17]

И в формулах Бальмера, и в формулах Ридберга используются целые числа: говоря современным языком, они подразумевают, что какое-то свойство атома квантовано. Понимание того, что это было за свойство и почему оно было квантовано, было важной частью развития квантовой механики, как показано в оставшейся части этой статьи.

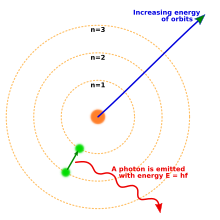
В Модель Бора атома, показывая электрон, переходящий с одной орбиты на другую, испуская фотон

В 1913 г. Нильс Бор предложенный новая модель атома это включало квантованные электронные орбиты: электроны все еще вращаются вокруг ядра так же, как планеты вращаются вокруг Солнца, но им разрешено жить только на определенных орбитах, а не на любом произвольном расстоянии.^[18] Когда атом излучал (или поглощал) энергию, электрон не двигался по непрерывной траектории от одной орбиты вокруг ядра к другой, как можно было бы ожидать в классической теории. Вместо этого электрон мгновенно перескочил бы с одной орбиты на другую, испуская излучаемый свет в виде фотона.^[19] Возможные энергии фотонов, испускаемых каждым элементом, определялись разницей в энергии между орбитами, и поэтому спектр излучения для каждого элемента будет содержать несколько линий.^[20]

Нильс Бор в молодости

Исходя только из одного простого предположения о правиле, которому должны подчиняться орбиты, модель Бора смогла связать наблюдаемые спектральные линии в спектре излучения водорода с ранее известными константами. В модели Бора электрону не разрешалось непрерывно излучать энергию и врезаться в ядро: как только он находился на ближайшей разрешенной орбите, он оставался стабильным навсегда. Модель Бора не объясняла, почему орбиты должны быть квантованы таким образом, и не могла сделать точных прогнозов для атомов с более чем одним электроном или объяснить, почему одни спектральные линии ярче других.

Некоторые фундаментальные предположения модели Бора вскоре оказались неверными, но ключевой результат, заключающийся в том, что дискретные линии в спектрах излучения обусловлены некоторыми свойствами электронов в квантованных атомах, верен. Фактическое поведение электронов разительно отличается от поведения атома Бора и от того, что мы видим в мире нашего повседневного опыта; обсуждается эта современная квантово-механическая модель атома. ниже.

Более подробное объяснение модели Бора

Бор предположил, что угловой момент, $L$ , электрона квантуется:

{ displaystyle L = n { frac {h} {2 pi}} = n hbar}

где $п$ целое число и $час$ - постоянная Планка. Исходя из этого предположения, Закон Кулона и уравнения круговое движение показать, что электрон с $п$ единиц углового момента орбиты протона на расстоянии $р$ данный

{ displaystyle r = { frac {n ^ {2} h ^ {2}} {4 pi ^ {2} k_ {e} me ^ {2}}}}

,

где $k е$ это Кулоновская постоянная, $м$ - масса электрона, а $е$ это заряд на электроне. Для простоты это записывается как

{ Displaystyle г = п ^ {2} а_ {0}, !}

где $а 0$ , называется Радиус Бора, равен 0,0529 нм. Боровский радиус - это радиус наименьшей допустимой орбиты.

Энергия электрона^{[примечание 6]} также может быть вычислен и определяется как

{ displaystyle E = - { frac {k _ { mathrm {e}} e ^ {2}} {2a_ {0}}} { frac {1} {n ^ {2}}}}

.

Таким образом, предположение Бора о квантовании углового момента означает, что электрон может населять только определенные орбиты вокруг ядра и что он может иметь только определенные энергии. Следствием этих ограничений является то, что электрон не врезается в ядро: он не может непрерывно излучать энергию и не может подойти к ядру ближе, чем а₀ (радиус Бора).

Электрон теряет энергию, мгновенно перескакивая со своей исходной орбиты на более низкую; дополнительная энергия испускается в виде фотона. И наоборот, электрон, который поглощает фотон, получает энергию и, следовательно, перескакивает на орбиту, расположенную дальше от ядра.

Каждый фотон светящегося атомарного водорода возникает из-за движения электрона с более высокой орбиты с радиусом $р п$ , на более низкую орбиту, $р м$ . Энергия $E γ$ этого фотона есть разница энергий $E п$ и $E м$ электрона:

{ displaystyle E _ { gamma} = E_ {n} -E_ {m} = { frac {k _ { mathrm {e}} e ^ {2}} {2a_ {0}}} left ({ frac {1} {m ^ {2}}} - { frac {1} {n ^ {2}}} right)}

Поскольку уравнение Планка показывает, что энергия фотона связана с длиной его волны соотношением $E γ = hc / λ$ , длины волн света, которые могут быть испущены, задаются

{ displaystyle { frac {1} { lambda}} = { frac {k _ { mathrm {e}} e ^ {2}} {2a_ {0} hc}} left ({ frac {1} {m ^ {2}}} - { frac {1} {n ^ {2}}} right).}

Это уравнение имеет тот же вид, что и Формула Ридберга, и предсказывает, что постоянная $р$ должен быть дан

{ displaystyle R = { frac {k _ { mathrm {e}} e ^ {2}} {2a_ {0} hc}}.}

Следовательно, модель атома Бора может предсказывать спектр излучения водорода с помощью фундаментальных констант.^{[примечание 7]} Однако он не смог сделать точных прогнозов для многоэлектронных атомов или объяснить, почему одни спектральные линии ярче других.

Дуальность волна-частица

Луи де Бройль в 1929 году. Де Бройль выиграл Нобелевская премия по физике за его предсказание, что материя действует как волна, сделанное в его докторской диссертации 1924 года.

Подобно тому, как свет имеет свойства как волны, так и частицы, материя также имеет волнообразные свойства.^[21]

Вещество, ведущее себя как волна, было впервые экспериментально продемонстрировано на электронах: пучок электронов может проявлять дифракция как луч света или водная волна.^{[примечание 8]} Позднее аналогичные волновые явления были показаны для атомов и даже молекул.

Длина волны, λ, связанный с любым объектом, связан с его импульсом, п, сквозь Постоянная Планка, час:^[22]^[23]

{ displaystyle p = { frac {h} { lambda}}.}

Это соотношение, называемое гипотезой де Бройля, справедливо для всех типов материи: вся материя проявляет свойства как частиц, так и волн.

Концепция дуальности волна-частица говорит о том, что ни классическая концепция «частицы», ни «волна» не может полностью описать поведение объектов квантового масштаба, будь то фотоны или материя. Дуальность волна – частица является примером принцип дополнительности в квантовой физике.^[24]^[25]^[26]^[27]^[28] Элегантный пример дуальности волна-частица, эксперимент с двойной щелью, обсуждается в следующем разделе.

Двухщелевой эксперимент

Дифракционная картина создается, когда свет проходит через одну щель (вверху), а интерференционная картина создается двумя щелями (внизу). Гораздо более сложная картина из двух щелей с мелкомасштабными интерференционными полосами демонстрирует волнообразное распространение света.

Воспроизвести медиа

Эксперимент с двойной щелью для классической частицы, волны и квантовой частицы, демонстрирующий дуальность волна-частица

В эксперименте с двумя щелями, первоначально проведенном Томас Янг в 1803 г.,^[29] а потом Огюстен Френель десять лет спустя^[29] луч света направляется через две узкие, близко расположенные щели, создавая картина интерференции светлых и темных полос на экране. Если одна из щелей закрыта, можно наивно ожидать, что интенсивность полос из-за интерференции повсюду уменьшится вдвое. На самом деле видна гораздо более простая картина: дифракционная картина диаметрально противоположно открытой щели. Точно такое же поведение может быть продемонстрировано в водных волнах, поэтому эксперимент с двумя щелями рассматривался как демонстрация волновой природы света.

Варианты эксперимента с двумя щелями были выполнены с использованием электронов, атомов и даже больших молекул.^[30]^[31] и виден такой же тип интерференционной картины. Таким образом было продемонстрировано, что все дело обладает как частицами, так и волновыми характеристиками.

Даже если интенсивность источника уменьшается, так что только одна частица (например, фотон или электрон) проходит через устройство за раз, со временем развивается та же интерференционная картина. Квантовая частица действует как волна при прохождении через двойные щели, но как частица при обнаружении. Это типичная особенность квантовой дополнительности: квантовая частица действует как волна в эксперименте для измерения своих волновых свойств и как частица в эксперименте для измерения своих частицоподобных свойств. Точка на экране детектора, в которой появляется любая отдельная частица, является результатом случайного процесса. Однако картина распределения многих отдельных частиц имитирует картину дифракции, создаваемую волнами.

Приложение к модели Бора

Де Бройль расширил Боровская модель атома показывая, что электрон на орбите вокруг ядра может рассматриваться как обладающий волнообразными свойствами. В частности, электрон соблюдается только в ситуациях, позволяющих стоячая волна вокруг ядро. Примером стоячей волны является струна скрипки, которая закреплена с обоих концов и может приводить в движение. Кажется, что волны, создаваемые струнным инструментом, колеблются на месте, перемещаясь от гребня к впадине вверх и вниз. Длина стоячей волны зависит от длины вибрирующего объекта и граничных условий. Например, поскольку струна скрипки закреплена с обоих концов, она может переносить стоячие волны длин волн. ${ displaystyle { frac {2l} {n}}}$ , где л это длина и п положительное целое число. Де Бройль предположил, что допустимыми электронными орбитами были такие, для которых окружность орбиты была бы целым числом длин волн. Следовательно, длина волны электрона определяет, что возможны только боровские орбиты на определенных расстояниях от ядра. В свою очередь, на любом расстоянии от ядра, меньшем определенного значения, невозможно установить орбиту. Минимально возможное расстояние от ядра называется радиусом Бора.^[32]

Трактовка де Бройля квантовых событий послужила отправной точкой для Шредингера, когда он намеревался построить волновое уравнение для описания квантовых теоретических событий.

Вращение

Воспроизвести медиа

Квантовый спин против классического магнита в Эксперимент Штерна-Герлаха

В 1922 г. Отто Стерн и Вальтер Герлах выстрелил атомами серебра через неоднородный магнитное поле. Относительно своего северного полюса, направленного вверх, вниз или где-то посередине, в классической механике магнит, брошенный через магнитное поле, может отклоняться на небольшое или большое расстояние вверх или вниз. Аналогичным образом действовали и атомы, которые Штерн и Герлах пробили через магнитное поле. Однако, хотя магниты можно было отклонять на переменное расстояние, атомы всегда отклонялись бы на постоянное расстояние вверх или вниз. Это означало, что свойство атома, которое соответствует ориентации магнита, должно быть квантовано, принимая одно из двух значений (вверх или вниз), в отличие от свободного выбора под любым углом.

Ральф Крониг возникла теория, согласно которой частицы, такие как атомы или электроны, ведут себя так, как если бы они вращались или «вращались» вокруг оси. Вращение учитывает недостающие магнитный момент,^{[требуется разъяснение ]} и позволить двум электронам на одной орбитали занимать разные квантовые состояния если они «вращаются» в противоположных направлениях, удовлетворяя тем самым принцип исключения. Квантовое число представляет смысл спина (положительный или отрицательный).

Выбор ориентации магнитного поля, используемого в эксперименте Штерна – Герлаха, произвольный. В показанной здесь анимации поле вертикальное, поэтому атомы отклоняются вверх или вниз. Если повернуть магнит на четверть оборота, атомы отклонятся влево или вправо. Использование вертикального поля показывает, что вращение вдоль вертикальной оси квантуется, а использование горизонтального поля показывает, что вращение вдоль горизонтальной оси квантуется.

Если вместо того, чтобы попасть в экран детектора, один из пучков атомов, выходящих из аппарата Штерна-Герлаха, попадает в другое (неоднородное) магнитное поле, ориентированное в том же направлении, все атомы отклоняются одинаково в эту секунду. поле. Однако, если второе поле ориентировано под углом 90 ° к первому, тогда половина атомов отклоняется в одну сторону, а половина - в другую, так что спин атома вокруг горизонтальной и вертикальной осей не зависит друг от друга. Однако, если один из этих лучей (например, атомы, которые были отклонены вверх, а затем влево) проходит в третье магнитное поле, ориентированное так же, как и первое, половина атомов движется в одну сторону, а половина в другую, даже если изначально шла в том же направлении. Действие измерения спина атомов относительно горизонтального поля изменило их спин относительно вертикального поля.

Эксперимент Штерна – Герлаха демонстрирует ряд важных особенностей квантовой механики:

Было продемонстрировано, что свойство природного мира квантовано и может принимать только определенные дискретные значения.
Частицы обладают внутренним угловой момент это очень похоже на угловой момент классически вращающегося объекта.
Измерение изменяет систему, измеряемую в квантовой механике. Можно знать только вращение объекта в одном направлении, а наблюдение за вращением в другом направлении разрушает исходную информацию о вращении.
Квантовая механика вероятностна: положительный или отрицательный спин любого отдельного атома, посланного в устройство, является случайным.

Развитие современной квантовой механики

В 1925 г. Вернер Гейзенберг попытался решить одну из проблем, на которую модель Бора оставила без ответа, объяснив интенсивности различных линий в спектре излучения водорода. Посредством ряда математических аналогий он выписал квантово-механический аналог для классического вычисления интенсивностей.^[33] Вскоре после этого коллега Гейзенберга Макс Борн понял, что метод Гейзенберга для расчета вероятностей переходов между различными уровнями энергии может быть лучше всего выражен с помощью математической концепции матрицы.^{[примечание 9]}

В том же году, основываясь на гипотезе де Бройля, Эрвин Шредингер разработал уравнение, описывающее поведение квантово-механической волны.^[34] Математическая модель, названная Уравнение Шредингера после своего создателя, занимает центральное место в квантовой механике, определяет разрешенные стационарные состояния квантовой системы и описывает, как квантовое состояние физической системы изменяется во времени.^[35] Сама волна описывается математической функцией, известной как "волновая функция Шредингер сказал, что волновая функция обеспечивает «средство для прогнозирования вероятности результатов измерения».^[36]

Шредингер смог вычислить уровни энергии водорода, рассматривая атомы водорода. электрон как классическая волна, движущаяся в яме электрического потенциала, созданного протоном. Этот расчет точно воспроизводит уровни энергии модели Бора.

В мае 1926 года Шредингер доказал, что теория Гейзенберга матричная механика и его собственный волновая механика сделал те же предсказания относительно свойств и поведения электрона; математически эти две теории имели общую форму. Тем не менее, двое мужчин разошлись во мнениях относительно интерпретации их общей теории. Например, Гейзенберг принял теоретическое предсказание скачков электронов между орбиталями в атоме:^[37] но Шредингер надеялся, что теория, основанная на свойствах непрерывной волны, сможет избежать того, что он называл (перефразируя словами Вильгельм Вена ) "этот бред про квантовые скачки".^[38] В конце концов подход Гейзенберга победил, и квантовые скачки подтвердились.^[39]

Копенгагенская интерпретация

В Институт Нильса Бора в Копенгагене, который был центром внимания исследователей квантовой механики и смежных дисциплин в 1920-х и 1930-х годах. Большинство самых известных в мире физиков-теоретиков проводили там время.

Бор, Гейзенберг и другие пытались объяснить, что на самом деле означают эти экспериментальные результаты и математические модели. Их описание, известное как копенгагенская интерпретация квантовой механики, было направлено на описание природы реальности, которая исследовалась посредством измерений и описывалась математическими формулировками квантовой механики.

Основные принципы копенгагенской интерпретации:

Система полностью описывается волновая функция, обычно обозначается греческой буквой ${ displaystyle psi}$ ("psi"). (Гейзенберг)
Как ${ displaystyle psi}$ изменения во времени задаются уравнением Шредингера.^{[требуется разъяснение ]}
Описание природы по своей сути вероятностное. Вероятность события - например, когда на экране появляется частица в эксперименте с двумя щелями - связана с квадратом абсолютного значения амплитуды ее волновой функции. (Родившееся правило, из-за Макс Борн, что придает физический смысл волновой функции в копенгагенской интерпретации: амплитуда вероятности )
Невозможно узнать значения всех свойств системы одновременно; те свойства, которые неизвестны с точностью, должны описываться вероятностями. (Гейзенберга принцип неопределенности )
Материя, как и энергия, демонстрирует дуальность волна-частица. Эксперимент может продемонстрировать свойства материи, подобные частицам, или ее волнообразные свойства; но не оба одновременно. (Принцип дополнительности из-за Бора)
Измерительные устройства по сути являются классическими устройствами и измеряют классические свойства, такие как положение и импульс.
Квантово-механическое описание больших систем должно близко приближаться к классическому описанию. (Принцип соответствия Бора и Гейзенберга)

Различные следствия этих принципов более подробно обсуждаются в следующих подразделах.

Принцип неопределенности

Вернер Гейзенберг в возрасте 26 лет. Гейзенберг выиграл Нобелевская премия по физике в 1932 году за работу, которую он делал примерно в это время.^[40]

Предположим, требуется измерить положение и скорость объекта - например, автомобиля, проезжающего через радарный датчик скорости. Можно предположить, что автомобиль имеет определенное положение и скорость в определенный момент времени. Насколько точно можно измерить эти значения, зависит от качества измерительного оборудования. Если точность измерительного оборудования улучшена, результат будет ближе к истинному значению. Можно было бы предположить, что скорость автомобиля и его положение могут быть оперативно определены и измерены одновременно, настолько точно, насколько это необходимо.

В 1927 году Гейзенберг доказал, что это последнее предположение неверно.^[41] Квантовая механика показывает, что определенные пары физических свойств, например положение и скорость, нельзя одновременно измерить или определить в эксплуатационных терминах с произвольной точностью: чем точнее измеряется или определяется одно свойство в операционных терминах, тем менее точно может быть Другой. Это заявление известно как принцип неопределенности. Принцип неопределенности - это не только утверждение о точности нашего измерительного оборудования, но, более глубоко, он касается концептуальной природы измеряемых величин - предположение о том, что автомобиль одновременно определял положение и скорость, не работает в квантовой механике. В масштабе автомобилей и людей эти неопределенности незначительны, но когда имеешь дело с атомами и электронами, они становятся критическими.^[42]

Гейзенберг привел в качестве иллюстрации измерение положения и импульса электрона с помощью фотона света. При измерении положения электрона, чем выше частота фотона, тем точнее измерение положения столкновения фотона с электроном, но тем больше возмущение электрона. Это связано с тем, что при столкновении с фотоном электрон поглощает случайное количество энергии, что приводит к измерению его импульс становится все более неопределенным (импульс - это скорость, умноженная на массу), поскольку необходимо измерять его возмущенный импульс после удара по продуктам столкновения, а не его исходный импульс. Для фотона с более низкой частотой возмущение (и, следовательно, неопределенность) в импульсе меньше, но также и точность измерения положения удара.^[43]

В основе принципа неопределенности лежит не загадка, а тот простой факт, что для любого математического анализа в областях положения и скорости (Анализ Фурье ), достижение более резкой (более точной) кривой в области положения может быть выполнено только за счет более плавной (менее точной) кривой в области скорости, и наоборот. Для большей резкости в области положения требуется вклад большего количества частот в области скорости для создания более узкой кривой, и наоборот. Это фундаментальный компромисс, присущий любой такой связанной или дополнительный измерений, но действительно заметен только в самом маленьком (планковском) масштабе, близком к размеру элементарные частицы.

Принцип неопределенности математически показывает, что произведение неопределенности положения и импульс частицы (импульс - это скорость, умноженная на массу) никогда не может быть меньше определенного значения, и это значение связано с Постоянная Планка.

Коллапс волновой функции

Коллапс волновой функции означает, что измерение вызвало или преобразовало квантовое (вероятностное или потенциальное) состояние в определенное измеренное значение. Это явление наблюдается только в квантовой механике, а не в классической механике.

Например, до того, как фотон действительно «появится» на экране обнаружения, его можно описать только с помощью набора вероятностей того, где он может появиться. Когда он появляется, например, в CCD Электронной камеры время и пространство, в котором она взаимодействовала с устройством, известны в очень жестких пределах. Однако фотон исчез в процессе захвата (измерения), а его квантовый волновая функция исчез вместе с ним. На его месте появилось какое-то макроскопическое физическое изменение на экране обнаружения, например, выставленное пятно на листе фотопленки или изменение электрического потенциала в какой-либо ячейке ПЗС-матрицы.

Собственные состояния и собственные значения

Более подробное введение в эту тему см .: Введение в собственные состояния

Из-за принцип неопределенности, утверждения о положении и импульсе частиц могут дать только вероятность что позиция или импульс имеет некоторое числовое значение. Следовательно, необходимо четко сформулировать разницу между состоянием чего-то неопределенного, например, электрона в облаке вероятности, и состоянием чего-то, имеющего определенное значение. Когда объект определенно может быть "прижат" в каком-то отношении, говорят, что он обладает собственное состояние.

В обсуждаемом эксперименте Штерна – Герлаха над, спин атома вокруг вертикальной оси имеет два собственных состояния: вверх и вниз. Прежде чем приступить к его измерению, мы можем только сказать, что любой отдельный атом с равной вероятностью будет обнаружен как имеющий вращение вверх или вниз. В процессе измерения волновая функция коллапсирует в одно из двух состояний.

Собственные состояния вращения вокруг вертикальной оси не являются одновременно собственными состояниями вращения вокруг горизонтальной оси, поэтому у этого атома с равной вероятностью будет обнаружено любое значение вращения вокруг горизонтальной оси. Как описано в разделе над измерение вращения вокруг горизонтальной оси может позволить атому, который был раскручен вверх, вращаться вниз: измерение его вращения вокруг горизонтальной оси коллапсирует его волновую функцию в одно из собственных состояний этого измерения, что означает, что он больше не находится в собственном состоянии вращение вокруг вертикальной оси, поэтому может принимать любое значение.

Принцип исключения Паули

Вольфганг Паули

В 1924 г. Вольфганг Паули предложили новую квантовую степень свободы (или квантовое число ) с двумя возможными значениями, чтобы устранить несоответствия между наблюдаемыми молекулярными спектрами и предсказаниями квантовой механики. В частности, спектр атомарного водорода имел дублет, или пара строк, отличающихся на небольшую величину, где ожидалась только одна строка. Паули сформулировал принцип исключения, заявляя: «Не может существовать атом в таком квантовом состоянии, чтобы два электрона внутри [него] имели одинаковый набор квантовых чисел».^[44]

Год спустя, Уленбек и Гоудсмит идентифицировал новую степень свободы Паули со свойством под названием вращение эффекты которого наблюдались в эксперименте Штерна – Герлаха.

Приложение к атому водорода

Модель атома Бора была по сути планетарной, с электронами, вращающимися вокруг ядерного «солнца». Однако принцип неопределенности гласит, что электрон не может одновременно иметь точное местоположение и скорость, как планета. Говорят, что вместо классических орбит электроны населяют атомные орбитали. Орбиталь - это «облако» возможных мест, в которых может быть обнаружен электрон, скорее распределение вероятностей, чем точное местоположение.^[44] Каждая орбиталь является трехмерной, а не двухмерной, и часто изображается как трехмерная область, внутри которой существует 95-процентная вероятность обнаружения электрона.^[45]

Шредингер смог вычислить уровни энергии водорода, рассматривая атомы водорода. электрон как волна, представленная "волновая функция " $Ψ$ , в электрический потенциал хорошо, $V$ , созданный протоном. Решения уравнения Шредингера^{[требуется разъяснение ]} представляют собой распределения вероятностей положений и положений электронов. Орбитали имеют разные формы в трех измерениях. Можно вычислить энергии различных орбиталей, и они точно соответствуют уровням энергии модели Бора.

В картине Шредингера каждый электрон обладает четырьмя свойствами:

«Орбитальное» обозначение, показывающее, является ли волна частицы той, которая находится ближе к ядру с меньшей энергией, или той, которая находится дальше от ядра с большей энергией;
«Форма» орбиты, сферическая или другая;
«Наклон» орбиты, определяющий магнитный момент орбиты вокруг $z$ -ось.
«Спин» электрона.

Общее название этих свойств - квантовое состояние электрона. Квантовое состояние можно описать, присвоив каждому из этих свойств номер; они известны как электронные квантовые числа. Квантовое состояние электрона описывается его волновой функцией. Принцип исключения Паули требует, чтобы никакие два электрона в атоме не имели одинаковых значений всех четырех чисел.

Формы атомных орбиталей. Ряды: 1s, 2п, 3d и 4ж. Слева направо

{ displaystyle m = -l, ldots, l}

. Цвета показывают фазу волновой функции.

Первое свойство, описывающее орбиталь, - это главное квантовое число, $п$ , что такое же, как в модели Бора. $п$ обозначает уровень энергии каждой орбитали. Возможные значения для $п$ целые числа:

{ Displaystyle п = 1,2,3 ldots}

Следующее квантовое число, азимутальное квантовое число, обозначенный $л$ , описывает форму орбитали. Форма является следствием угловой момент орбиты. Угловой момент представляет собой сопротивление вращающегося объекта ускорению или замедлению под действием внешней силы. Азимутальное квантовое число представляет собой орбитальный угловой момент электрона вокруг его ядра. Возможные значения для $л$ целые числа от 0 до $п - 1$ (где $п$ - главное квантовое число электрона):

{ displaystyle l = 0,1, ldots, n-1.}

Форма каждой орбитали обычно обозначается буквой, а не ее азимутальным квантовым числом. Первая фигура ( $л$ = 0) обозначается буквой $s$ (а мнемонический быть "sphere "). Следующая фигура обозначается буквой $п$ и имеет форму гантели. Остальные орбитали имеют более сложную форму (см. атомная орбиталь ), и обозначаются буквами $d$ , $ж$ , $г$ , так далее.

Третье квантовое число, магнитное квантовое число, описывает магнитный момент электрона, и обозначается $м л$ (или просто м). Возможные значения для $м л$ целые числа из $- л$ к $л$ (где $л$ - азимутальное квантовое число электрона):

{ displaystyle m_ {l} = - l, - (l-1), ldots, 0,1, ldots, l.}

Магнитное квантовое число измеряет компонент углового момента в определенном направлении. Выбор направления произвольный; обычно выбирается z-направление.

Четвертое квантовое число, квантовое число спина (относящийся к «ориентации» спина электрона) обозначается $м s$ , со значениями +¹⁄₂ или -¹⁄₂.

Химик Линус Полинг написал, в качестве примера:

В случае гелий атом с двумя электронами в 1s орбитально, принцип исключения Паули требует, чтобы два электрона различались значением одного квантового числа. Их ценности $п$ , $л$ , и $м л$ такие же. Соответственно они должны отличаться по стоимости $м s$ , который может иметь значение +¹⁄₂ на один электрон и -¹⁄₂ для другого ".^[44]

Это основная структура и симметрия атомных орбиталей, а также то, как электроны заполняют их, что приводит к организации атомных орбиталей. периодическая таблица. Как атомные орбитали на разных атомах объединяются, чтобы сформировать молекулярные орбитали определяет структуру и прочность химических связей между атомами.

Волновое уравнение Дирака

Поль Дирак (1902–1984)

В 1928 г. Поль Дирак расширил Уравнение Паули, описывающего вращающиеся электроны, для учета специальная теория относительности. Результатом стала теория, которая должным образом рассматривала такие события, как скорость, с которой электрон вращается вокруг ядра, происходящие на значительной части скорость света. Используя простейший электромагнитное взаимодействие, Дирак смог предсказать значение магнитного момента, связанного со спином электрона, и обнаружил экспериментально наблюдаемое значение, которое было слишком большим, чтобы соответствовать величине вращающейся заряженной сферы, управляемой классическая физика. Он смог решить спектральные линии атома водорода, и воспроизвести из первых физических принципов Зоммерфельд формула успеха тонкая структура спектра водорода.

Уравнения Дирака иногда давали отрицательное значение энергии, для чего он предложил новое решение: он постулировал существование антиэлектрон и динамического вакуума. Это привело к многочастичной квантовая теория поля.

Квантовая запутанность

Суперпозиция двух квантовых характеристик и две возможности разрешения.

Принцип исключения Паули гласит, что два электрона в одной системе не могут находиться в одном и том же состоянии. Однако природа оставляет открытой возможность, что два электрона могут иметь оба состояния, «наложенные» на каждое из них. Напомним, что волновые функции, которые одновременно выходят из двойных щелей, попадают на экран детектирования в состоянии суперпозиции. Ничто не является определенным до тех пор, пока наложенные сигналы не «схлопнутся». В этот момент электрон появляется где-то в соответствии с вероятностью, которая является квадратом абсолютного значения суммы комплексных амплитуд двух наложенных друг на друга сигналов. Ситуация там уже очень абстрактная. Конкретный способ размышления о запутанных фотонах, фотонах, в которых два противоположных состояния накладываются на каждый из них в одном и том же событии, выглядит следующим образом:

Представьте, что у нас есть два состояния фотонов с цветовой кодировкой: одно состояние помечено синий и другой штат помечен красный. Пусть суперпозиция красного и синего состояний проявляется (в воображении) как фиолетовый штат. Мы рассматриваем случай, когда два фотона образуются в результате одного атомного события. Возможно, они вызваны возбуждением кристалла, который обычно поглощает фотон определенной частоты и испускает два фотона с половиной исходной частоты.В этом случае фотоны связаны друг с другом общим происхождением в одном атомном событии. Эта установка приводит к наложению состояний фотонов. Итак, два фотона выходят фиолетовый. Если экспериментатор сейчас проведет какой-нибудь эксперимент, который определяет, является ли один из фотонов синий или красный, то этот эксперимент изменяет вовлеченный фотон с фотона, имеющего суперпозицию синий и красный характеристики фотона, который имеет только одну из этих характеристик. Проблема, с которой столкнулся Эйнштейн с такой воображаемой ситуацией, заключалась в том, что если бы один из этих фотонов продолжал прыгать между зеркалами в лаборатории на Земле, а другой прошел бы половину пути к ближайшей звезде, то его двойник должен был проявить себя как синий или красный, это означало, что удаленный фотон теперь должен был потерять фиолетовый статус тоже. Поэтому всякий раз, когда его можно было исследовать после измерения его близнеца, он обязательно обнаруживался бы в состоянии, противоположном тому, что обнаружил его близнец.

Пытаясь показать, что квантовая механика не является законченной теорией, Эйнштейн начал с предсказания теории о том, что две или более частицы, которые взаимодействовали в прошлом, могут оказаться сильно коррелированными при последующем измерении их различных свойств. Он стремился объяснить это кажущееся взаимодействие классическим способом, через их общее прошлое, а желательно не какими-то «жуткими действиями на расстоянии». Аргумент разработан в известной статье Эйнштейн, Подольский и Розен (1935; сокращенно EPR), в которой излагается то, что сейчас называется Парадокс ЭПР. Предполагая, что сейчас обычно называют местный реализм, ЭПР попытался показать из квантовой теории, что частица имеет и положение, и импульс одновременно, в то время как согласно Копенгагенская интерпретация, только одно из этих двух свойств действительно существует и только в тот момент, когда оно измеряется. ЭПР пришел к выводу, что квантовая теория неполна, поскольку она отказывается рассматривать физические свойства, которые объективно существуют в природе. (Einstein, Podolsky, & Rosen 1935 в настоящее время является наиболее цитируемой публикацией Эйнштейна в физических журналах.) В том же году Эрвин Шредингер использовал слово «запутанность» и заявил: «Я бы не назвал это один скорее то характерная черта квантовой механики ».^[46] С тех пор, как ирландский физик Джон Стюарт Белл теоретически и экспериментально опроверг теорию "скрытых переменных" Эйнштейна, Подольского и Розена, большинство физиков приняли запутанность как реальное явление.^[47] Однако есть некоторый спор меньшинства.^[48] В Неравенства Белла являются самым мощным вызовом утверждениям Эйнштейна.

Квантовая теория поля

Идея квантовой теории поля зародилась в конце 1920-х годов с британского физика. Поль Дирак, когда он попытался квантовать энергия электромагнитное поле; так же, как в квантовой механике, квантовалась энергия электрона в атоме водорода. Квантование - это процедура построения квантовой теории, начиная с классической теории.

Мерриам-Вебстер определяет поле в физике как «область или пространство, в котором заданный эффект (например, магнетизм ) существуют".^[49] Другие эффекты, проявляющиеся в виде полей: гравитация и статичное электричество.^[50] В 2008 году физик Ричард Хаммонд написал:

Иногда мы различаем квантовую механику (КМ) и квантовую теорию поля (КТП). КМ относится к системе, в которой количество частиц фиксировано, а поля (такие как электромеханическое поле) являются непрерывными классическими объектами. QFT ... идет дальше и позволяет создавать и уничтожать частицы ...

Однако он добавил, что квантовая механика часто используется для обозначения «всего понятия квантовой точки зрения».^[51]^:108

В 1931 году Дирак предположил существование частиц, которые позже стали известны как антивещество.^[52] Дирак поделился Нобелевская премия по физике на 1933 год с Шредингер "за открытие новых продуктивных форм атомная теория ".^[53]

На первый взгляд, квантовая теория поля допускает бесконечное число частиц и оставляет на усмотрение самой теории предсказывать, сколько и с какими вероятностями или числами они должны существовать. При дальнейшем развитии теория часто противоречит наблюдениям, так что ее операторы создания и уничтожения могут быть связаны эмпирически.^{[требуется разъяснение ]} Кроме того, эмпирические законы сохранения, такие как закон масса – энергия предлагают определенные ограничения на математическую форму теории, которые с математической точки зрения привередливы. Последний факт затрудняет работу с квантовыми теориями поля, но также привел к дальнейшим ограничениям на допустимые формы теории; осложнения упомянуты ниже под рубрикой перенормировка.

Квантовая электродинамика

Квантовая электродинамика (КЭД) - это название квантовой теории электромагнитная сила. Понимание QED начинается с понимания электромагнетизм. Электромагнетизм можно назвать электродинамикой, потому что это динамическое взаимодействие между электрическим и магнитные силы. Электромагнетизм начинается с электрический заряд.

Электрические заряды являются источниками и создают электрические поля. Электрическое поле - это поле, которое воздействует на любые частицы, несущие электрические заряды, в любой точке пространства. Сюда входят электрон, протон и даже кварки, среди прочего. При приложении силы электрические заряды перемещаются, течет ток и создается магнитное поле. Изменяющееся магнитное поле, в свою очередь, вызывает электрический ток (часто движущиеся электроны). Физическое описание взаимодействия заряженные частицы, электрические токи, электрические поля и магнитные поля называются электромагнетизм.

В 1928 г. Поль Дирак создал релятивистскую квантовую теорию электромагнетизма. Это был прародитель современной квантовой электродинамики, поскольку он содержал существенные компоненты современной теории. Однако проблема неразрешимых бесконечностей развивалась в этом релятивистская квантовая теория. Лет спустя, перенормировка во многом решил эту проблему. Первоначально рассматриваемая некоторыми из ее создателей как подозрительная временная процедура, перенормировка в конечном итоге стала важным и самосогласованным инструментом в КЭД и других областях физики. Также в конце 1940-х гг. Диаграммы Фейнмана изображены все возможные взаимодействия, относящиеся к данному событию. Диаграммы показали, в частности, что электромагнитная сила - это обмен фотонами между взаимодействующими частицами.^[54]

В Баранина сдвиг является примером предсказания квантовой электродинамики, которое было экспериментально подтверждено. Это эффект, при котором квантовая природа электромагнитного поля заставляет уровни энергии в атоме или ионе незначительно отклоняться от того, чем они были бы в противном случае. В результате спектральные линии могут сдвигаться или расщепляться.

Точно так же внутри свободно распространяющейся электромагнитной волны ток может быть просто абстрактным ток смещения вместо носителей заряда. В QED его полное описание существенно использует недолговечные виртуальные частицы. Там QED снова подтверждает более раннюю, довольно загадочную концепцию.

Стандартная модель

В 1960-е годы физики понял, что QED ломается при чрезвычайно высоких энергиях.^{[нужна цитата ]} Из-за этого несоответствия Стандартная модель физики элементарных частиц, которая исправила нарушение теории более высоких энергий. Это еще одна расширенная квантовая теория поля, объединяющая электромагнитное и слабые взаимодействия в одну теорию. Это называется электрослабая теория.

Дополнительно Стандартная модель содержит^{[нужна цитата ]} высокоэнергетическое объединение электрослабой теории с сильная сила, описанный квантовая хромодинамика. Он также постулирует связь с сила тяжести как еще один калибровочная теория, но связь по состоянию на 2015 год все еще плохо изучена. Успешное предсказание теории Частица Хиггса объяснение инертной массы было подтверждено Большой адронный коллайдер,^[55] и поэтому Стандартная модель теперь считается основным и более или менее полным описанием физика элементарных частиц как мы это знаем.

Интерпретации

Физические измерения, уравнения и предсказания, относящиеся к квантовой механике, согласованы и имеют очень высокий уровень подтверждения. Однако вопрос о том, что эти абстрактные модели говорят о сущности реального мира, получил разные ответы. Эти интерпретации очень разнообразны и иногда несколько абстрактны. Например, Копенгагенская интерпретация утверждает, что перед измерением утверждения о свойствах частицы совершенно бессмысленны, а в Интерпретация многих миров описывает существование мультивселенная состоит из всевозможных вселенных.^[56]

Приложения

Приложения квантовой механики включают лазер, то транзистор, то электронный микроскоп, и магнитно-резонансная томография. Особый класс квантово-механических приложений связан с макроскопические квантовые явления такие как сверхтекучий гелий и сверхпроводники. Изучение полупроводников привело к изобретению диод и транзистор, которые незаменимы для современных электроника.

Даже в простом выключатель, квантовое туннелирование абсолютно жизненно важно, так как в противном случае электроны в электрический ток не может проникнуть через потенциальный барьер, состоящий из слоя оксида. Флэш-память чипсы, найденные в USB-накопители также используют квантовое туннелирование, чтобы стереть свои ячейки памяти.^[57]

Смотрите также

Заметки

^ Был создан ряд формул, которые могли описать некоторые экспериментальные измерения теплового излучения: как длина волны, на которой излучение наиболее сильно изменяется с температурой, определяется выражением Закон смещения Вина, общая мощность, излучаемая на единицу площади, определяется как Закон Стефана – Больцмана. Лучшим теоретическим объяснением экспериментальных результатов было Закон Рэлея – Джинса, что хорошо согласуется с экспериментальными результатами на больших длинах волн (или, что то же самое, низких частотах), но сильно не согласуется с короткими длинами волн (или высоких частот). Фактически, на коротких волнах классическая физика предсказывала, что энергия будет излучаться горячим телом с бесконечной скоростью. Этот явно неверный результат известен как ультрафиолетовая катастрофа.
^ Слово квант исходит из Латинское слово для "сколько" (как и количество). То, что есть квантованный, как и энергия гармонических осцилляторов Планка, может принимать только определенные значения. Например, в большинстве стран деньги квантуются эффективно, а количество денег монета с наименьшей стоимостью в обращении. Механика - это отрасль науки, изучающая действие сил на объекты. Итак, квантовая механика - это часть механики, которая имеет дело с объектами, для которых квантованы определенные свойства.
^ Фактически, могут быть эффекты, зависящие от интенсивности, но при интенсивностях, достижимых с помощью нелазерных источников, эти эффекты не наблюдаются.
^ Уравнение фотоэлектрического эффекта Эйнштейна мочь быть выведенным и объясненным без требуя понятия «фотоны». То есть электромагнитное излучение можно рассматривать как классическую электромагнитную волну, если электроны в материале обрабатываются законами квантовой механики. Результаты количественно верны для тепловых источников света (солнце, лампы накаливания и т. Д.) Как по скорости эмиссии электронов, так и по их угловому распределению. Подробнее об этом см.^[14]
^ Классическая модель атома называется планетарной, а иногда и планетарной. Модель Резерфорда -после Эрнест Резерфорд который предложил его в 1911 году на основе Эксперимент с золотой фольгой Гейгера – Марсдена, который впервые продемонстрировал существование ядра.
^ В этом случае энергия электрона равна сумме его энергии. кинетический и потенциал энергии. Электрон имеет кинетическую энергию в силу своего фактического движения вокруг ядра и потенциальную энергию из-за своего электромагнитного взаимодействия с ядром.
^ Модель может быть легко модифицирована для учета спектра излучения любой системы, состоящей из ядра и одного электрона (т. Е. ионы такие как он⁺ или O⁷⁺, которые содержат только один электрон), но не могут быть расширены до атома с двумя электронами, такого как нейтральный гелий.
^ Электронная дифракция была впервые продемонстрирована через три года после того, как де Бройль опубликовал свою гипотезу. На Университет Абердина, Джордж Томсон пропускал пучок электронов через тонкую металлическую пленку и наблюдал дифракционные картины, как и предполагала гипотеза де Бройля. В Bell Labs, Дэвиссон и Germer направил электронный луч через кристаллическую решетку. Де Бройль был награжден Нобелевская премия по физике в 1929 г. за свою гипотезу; Томсон и Дэвиссон разделили Нобелевскую премию по физике в 1937 году за свои экспериментальные работы.
^ Более сложный взгляд на то, как Гейзенберг перешел от старой квантовой теории и классической физики к новой квантовой механике, см. Путь Гейзенберга к матричной механике.

использованная литература

^ "Квантовая механика". Национальное общественное радио. Получено 22 июн 2016.
^ Кун, Томас С. Структура научных революций. Четвертое изд. Чикаго; Лондон: Издательство Чикагского университета, 2012. Печать.
^ «Введение в квантовую механику». Socratease. Архивировано из оригинал 15 сентября 2017 г.
^ Фейнман, Ричард П. (1988). КЭД: странная теория света и материи (1-й принстонский пбк., Седьмое издание с исправлениями. Ред.). Принстон, Нью-Джерси: Издательство Принстонского университета. стр.10. ISBN 978-0691024172.
^ Этот результат был опубликован (на немецком языке) как Планк, Макс (1901). "Ueber das Gesetz der Energieverteilung im Normalspectrum" (PDF). Анна. Phys. 309 (3): 553–63. Bibcode:1901АнП ... 309..553П. Дои:10.1002 / andp.19013090310. Архивировано из оригинал (PDF) 10 июня 2012 г.. Английский перевод: «О законе распределения энергии в нормальном спектре». Архивировано из оригинал 18 апреля 2008 г.
^ Фрэнсис Уэстон Сирс (1958). Механика, волновое движение и тепло. Эддисон-Уэсли. п. 537.
^ "Нобелевская премия по физике 1918 г.". Нобелевский фонд. Получено 1 августа 2009.
^ Краг, Хельге (1 декабря 2000 г.). «Макс Планк: упорный революционер». PhysicsWorld.com.
^ Эйнштейн, Альберт (1905). "Über einen die Erzeugung und Verwandlung des Lichtes betreffenden heuristischen Gesichtspunkt" (PDF). Annalen der Physik. 17 (6): 132–48. Bibcode:1905AnP ... 322..132E. Дои:10.1002 / andp.19053220607., переводится на английский как Об эвристической точке зрения на производство и преобразование света В архиве 11 июня 2009 г. Wayback Machine. Термин «фотон» был введен в 1926 году.
^ «Возрождение волновой теории света в начале девятнадцатого века». www.encyclopedia.com. Получено 16 октября 2018.
^ ^а ^б ^c ^d ^е Taylor, J. R .; Zafiratos, C.D .; Дубсон, М.А. (2004). Современная физика для ученых и инженеров. Прентис Холл. С. 127–29. ISBN 0135897890.
^ Хокинг, Стивен (2001). Вселенная в двух словах. Петух. ISBN 978-0553802023.
^ Дике, Роберт Генри; Виттке, Джеймс П. (1960). Введение в квантовую механику. Издательство Эддисон-Уэсли. п. 12. ISBN 978-0201015102.
^ Lamb, Willis E., Jr .; Скалли, Марлан О. «Фотоэлектрический эффект без фотонов» (PDF). NTRS.NASA.gov.
^ Джим Лукас: «Что такое ультрафиолетовый свет?», 15 сентября 2017 г., livescience.com Доступ 27 декабря 2017 г.
^ 'Два уравнения, управляющие поведением света: часть вторая E = hν' на сайте chemteam.info Доступ 27 декабря 2017 г.
^ ^а ^б Taylor, J. R .; Zafiratos, C.D .; Дубсон, М.А. (2004). Современная физика для ученых и инженеров. Прентис Холл. С. 147–48. ISBN 0135897890.
^ McEvoy, J. P .; Зарате, О. (2004). Введение в квантовую теорию. Тотемные книги. С. 70–89, [89]. ISBN 1840465778.
^ Всемирная книжная энциклопедия, стр.6, 2007.^{[требуется полная цитата ]}
^ Дике и Виттке, Введение в квантовую механику, п. 10f.
^ McEvoy, J. P .; Зарате, О. (2004). Введение в квантовую теорию. Тотемные книги. С. 110 и далее. ISBN 1840465778.
^ Акзель, Амир Д., Запутанность, стр. 51 и далее. (Пингвин, 2003) ISBN 978-1551926476
^ McEvoy, J. P .; Зарате, О. (2004). Введение в квантовую теорию. Тотемные книги. п. 114. ISBN 1840465778.
^ Зеттили, Нуредин (2009). Квантовая механика: концепции и приложения. Джон Уайли и сыновья. С. 26–27. ISBN 978-0470026786.
^ Селлери, Франко (2012). Двойственность волны и частицы. Springer Science and Business Media. п. 41. ISBN 978-1461533320.
^ Подгорсак, Эрвин Б. (2013). Сборник по радиационной физике для медицинских физиков. Springer Science and Business Media. п. 88. ISBN 978-3642201868.
^ Холлидей, Дэвид; Резник, Роберт (2013). Основы физики, 10-е изд.. Джон Уайли и сыновья. п. 1272. ISBN 978-1118230619.
^ Майерс, Расти Л. (2006). Основы физики. Издательская группа «Гринвуд». стр.172. ISBN 0313328579. Принцип дополнительности волновой корпускулярный дуализм.
^ ^а ^б Шамос, Моррис Х (1 января 1987 г.). Великие эксперименты в физике: отчеты из первых рук от Галилея до Эйнштейна. Курьерская корпорация. п. 108.
^ Мерали, Зея (21 мая 2015 г.). «Квантовая физика: что на самом деле реально?». Природа. С. 278–80. Bibcode:2015Натура.521..278М. Дои:10.1038 / 521278a. Получено 7 января 2017.
^ Эйбенбергер, Сандра (2013). «Материя – волна интерференции частиц, выбранных из молекулярной библиотеки с массами, превышающими 10 000 а.е.м.». Физическая химия Химическая физика. 15 (35): 14696–700. arXiv:1310.8343. Bibcode:2013PCCP ... 1514696E. Дои:10.1039 / C3CP51500A. PMID 23900710. S2CID 3944699. [I] В интерферометре с тремя решетками ... Мы наблюдаем высококонтрастные структуры квантовых полос молекул ... имеющих 810 атомов в одной частице.
^ McEvoy, J. P .; Зарате, О. (2004). Введение в квантовую теорию. Тотемные книги. п. 87. ISBN 1840465778.
^ Ван дер Варден, Б. Л. (1967). Источники квантовой механики. Минеола, Нью-Йорк: Dover Publications. С. 261–76. Поступило 29 июля 1925 г. См. Статью Вернера Гейзенберга "Квантовая теоретическая переинтерпретация кинематических и механических соотношений", стр. 261–76.
^ Организация Нобелевской премии. "Эрвин Шредингер - Биографический". Получено 28 марта 2014. Его великое открытие - волновое уравнение Шредингера - было сделано в конце этой эпохи - в первой половине 1926 года.
^ «Уравнение Шредингера (физика)», Британская энциклопедия
^ Эрвин Шредингер, "Современная ситуация в квантовой механике", стр. 9. "Этот перевод был первоначально опубликован в Proceedings of the American Philosophical Society, 124, 323–388, а затем появился как Раздел I.11 Части I Квантовой теории и измерений (JA Wheeler and WH Zurek, eds., Princeton University Press, NJ 1983). Эту статью можно скачать здесь: Эрвин Шредингер. "Перевод статьи Шредингера" Кошачий парадокс."". Перевод Джона Д. Триммера. Архивировано из оригинал 13 ноября 2010 г.
^ Гейзенберг, В. (1955). Развитие интерпретации квантовой теории, стр. 12–29 в Нильс Бор и развитие физики: очерки, посвященные Нильсу Бору по случаю его семидесятилетия, Отредактировано Паули, В. с помощью Розенфельд, Л. и Вайскопф, В., Пергамон, Лондон, стр. 13: «единичный квантовый скачок ... является фактическим по своей природе».
^ В. Мур, Шредингер: жизнь и мысль, Cambridge University Press (1989), стр. 222. См. Стр. 227 по собственным словам Шредингера.
^ «Физики наконец-то увидят квантовый скачок собственными глазами». Нью-Йорк Таймс. Получено 30 ноября 2019.
^ "Нобелевская премия по физике 1932 г.". NobelPrize.org.
^ Гейзенберг впервые опубликовал свою работу о принципе неопределенности в ведущем немецком физическом журнале. Zeitschrift für Physik: Гейзенберг, В. (1927). "Über den anschaulichen Inhalt der quantentheoretischen Kinematik und Mechanik". Z. Phys. 43 (3–4): 172–98. Bibcode:1927ZPhy ... 43..172H. Дои:10.1007 / BF01397280. S2CID 122763326.
^ "Нобелевская премия по физике 1932 г.". NobelPrize.org.
^ «Принцип неопределенности», Британская энциклопедия
^ ^а ^б ^c Полинг, Линус (1960). Природа химической связи (3-е изд.). Итака, Нью-Йорк: Издательство Корнельского университета. п.47. ISBN 0801403332. Получено 1 марта 2016.
^ «Орбиталь (химия и физика)», Британская энциклопедия
^ Э. Шредингер, Труды Кембриджского философского общества, 31 (1935), с. 555, говорит: «Когда две системы, состояния которых мы знаем по их соответствующему представлению, вступают во временное физическое взаимодействие из-за известных сил между ними, и когда после некоторого времени взаимного влияния системы снова разделяются, тогда они больше не могут можно описать так же, как и раньше, а именно, наделив каждого из них своим собственным представителем. Я бы не назвал это один скорее то характерная черта квантовой механики ».
^ Дэвид Кайзер, Реальна ли квантовая запутанность?, The New York Times, ноябрь 2014 г.
^ Джон Г. Крамер. «Квантовая нелокальность и возможность сверхсветовых эффектов». npl.washington.edu. Архивировано из оригинал 29 декабря 2010 г.
^ «Механика», Онлайн-словарь Merriam-Webster
^ "Поле", Британская энциклопедия
^ Ричард Хаммонд, Неизвестная Вселенная, New Page Books, 2008. ISBN 978-1601630032
^ «Избранные физики - Поль Дирак 1902–1984». www.physicalworld.org.
^ «Нобелевская премия по физике 1933 года». Нобелевский фонд. Получено 24 ноября 2007.
^ «Обменные частицы». hyperphysics.phy-astr.gsu.edu. Получено 16 октября 2018.
^ «Десять лет открытий Большого адронного коллайдера под швейцарской сельской местностью - это только начало расшифровки Вселенной». www.thelocal.ch. 5 октября 2018 г.. Получено 16 октября 2018.
^ "Копенгагенская интерпретация". abyss.uoregon.edu. Получено 16 октября 2018.
^ Дуррани, З. А. К .; Ахмед, Х. (2008). Виджай Кумар (ред.). Нанокремний. Эльзевир. п. 345. ISBN 978-0080445281.

Список используемой литературы

Бернштейн, Джереми (2005). «Макс Борн и квантовая теория». Американский журнал физики. 73 (11): 999–1008. Bibcode:2005AmJPh..73..999B. Дои:10.1119/1.2060717.
Беллер, Мара (2001). Квантовый диалог: совершение революции. Издательство Чикагского университета.
Бор, Нильс (1958). Атомная физика и человеческие знания. Джон Вили и сыновья]. ISBN 0486479285. OCLC 530611.
де Бройль, Луи (1953). Революция в физике. Noonday Press. LCCN 53010401.
Броннер, Патрик; Струнц, Андреас; Зильберхорн, Кристина; Мейн, Ян-Питер (2009). «Демонстрация квантовой случайности с одиночными фотонами». Европейский журнал физики. 30 (5): 1189–1200. Bibcode:2009EJPh ... 30.1189B. Дои:10.1088/0143-0807/30/5/026.
Эйнштейн, Альберт (1934). Очерки науки. Философская библиотека. ISBN 0486470113. LCCN 55003947.
Фейгл, Герберт; Бродбек, май (1953). Чтения по философии науки. Appleton-Century-Crofts. ISBN 0390304883. LCCN 53006438.
Фейнман, Ричард П. (1949). "Пространственно-временной подход к квантовой электродинамике" (PDF). Физический обзор. 76 (6): 769–89. Bibcode:1949ПхРв ... 76..769Ф. Дои:10.1103 / PhysRev.76.769.^{[постоянная мертвая ссылка ]}
Фейнман, Ричард П. (1990). QED, Странная теория света и материи. Книги пингвинов. ISBN 978-0140125054.
Фаулер, Майкл (1999). Атом Бора. Университет Вирджинии.^{[ISBN отсутствует ]}
Гейзенберг, Вернер (1958). Физика и философия. Харпер и братья. ISBN 0061305499. LCCN 99010404.
Лакшмибала, С. (2004). «Гейзенберг, Матричная механика и принцип неопределенности». Резонанс: журнал естественно-научного образования. 9 (8): 46–56. Дои:10.1007 / bf02837577. S2CID 29893512.
Либофф, Ричард Л. (1992). Введение в квантовую механику (2-е изд.).^{[ISBN отсутствует ]}
Линдси, Роберт Брюс; Маргенау, Генри (1957). Основы физики. Дувр. ISBN 0918024188. LCCN 57014416.
McEvoy, J. P .; Зарате, Оскар (2004). Введение в квантовую теорию. ISBN 1874166374.
Неф, Карл Род (2005). "Квантовая физика". Гиперфизика. Государственный университет Джорджии.
Торф, Ф. Дэвид (2002). От уверенности к неопределенности: история науки и идей XXI века. Джозеф Генри Пресс.
Райхенбах, Ганс (1944). Философские основы квантовой механики. Калифорнийский университет Press. ISBN 0486404595. LCCN a44004471.
Шлипп, Пол Артур (1949). Альберт Эйнштейн: философ-ученый. Издательство "Тюдор". LCCN 50005340.
Читатель журнала Scientific American, 1953.
Сирс, Фрэнсис Уэстон (1949). Оптика (3-е изд.). Эддисон-Уэсли. ISBN 0195046013. LCCN 51001018.
Шимони, А. (1983). «(название не приводится в цитировании)». Основы квантовой механики в свете новых технологий (С. Камефучи и др., Ред.). Токио: Японское физическое общество. п. 225.; цитируется в: Попеску, Санду; Даниэль Рорлих (1996). «Действие и страсть на расстоянии: эссе в честь профессора Абнера Шимони». arXiv:Quant-ph / 9605004.
Тавель, Мортон; Тавель, Джудит (иллюстрации) (2002). Современная физика и пределы знаний. Издательство Университета Рутгерса. ISBN 978-0813530772.
Ван Флек, Дж. Х., 1928, "Принцип соответствия в статистической интерпретации квантовой механики", Proc. Natl. Акад. Sci. 14: 179.
Уэстморленд; Бенджамин Шумахер (1998). «Квантовая запутанность и отсутствие сверхсветовых сигналов». arXiv:Quant-ph / 9801014.
Уилер, Джон Арчибальд; Фейнман, Ричард П. (1949). «Классическая электродинамика в терминах прямого межчастичного действия» (PDF). Обзоры современной физики. 21 (3): 425–33. Bibcode:1949РвМП ... 21..425Вт. Дои:10.1103 / RevModPhys.21.425.
Виман, Карл; Перкинс, Кэтрин (2005). «Преобразование физического образования». Физика сегодня. 58 (11): 36. Bibcode:2005ФТ .... 58к..36Вт. Дои:10.1063/1.2155756.

дальнейшее чтение

Следующие заголовки, написанные физиками, пытаются донести квантовую теорию до непрофессионалов, используя минимум технических средств.

Джим Аль-Халили (2003) Quantum: руководство для недоумевших. Вайденфельд и Николсон. ISBN 978-1780225340
Честер, Марвин (1987) Учебник по квантовой механике. Джон Вили. ISBN 0486428788
Брайан Кокс и Джефф Форшоу (2011) Квантовая Вселенная. Аллен Лейн. ISBN 978-1846144325
Ричард Фейнман (1985) QED: странная теория света и материи. Издательство Принстонского университета. ISBN 0691083886
Форд, Кеннет (2005) Квантовый мир. Harvard Univ. Нажмите. Включает физику элементарных частиц.
Гирарди, Джанкарло (2004) Краем глаза на карты Бога, Джеральд Мальсбари, пер. Princeton Univ. Нажмите. Самая техническая из цитируемых здесь работ. Переходы с использованием алгебра, тригонометрия, и обозначение бюстгальтера можно пропустить при первом чтении.
Тони Эй и Уолтерс, Патрик (2003) Новая квантовая вселенная. Cambridge Univ. Нажмите. Включает многое о технологиях, которые стала возможной благодаря квантовой теории. ISBN 978-0521564571
Иванчевич Владимир Г., Иванцевич Тияна Т. (2008 г.) Квантовый скачок: от Дирака и Фейнмана через вселенную к человеческому телу и разуму. Всемирная научная издательская компания. Предоставляет интуитивно понятное введение в нематематических терминах и введение в сравнительно простых математических терминах. ISBN 978-9812819277
Н. Дэвид Мермин (1990) «Жуткие действия на расстоянии: загадки QT» в его Буджумы полностью. Cambridge Univ. Пресс: 110–76. Автор - редкий физик, который пытается общаться с философами и гуманистами. ISBN 978-0521388801
Роланд Омнес (1999) Понимание квантовой механики. Princeton Univ. Нажмите. ISBN 978-0691004358
Виктор Стенгер (2000) Вневременная реальность: симметрия, простота и множественность вселенных. Буффало Нью-Йорк: Книги Прометея. Гл. 5–8. ISBN 978-1573928595
Мартинус Вельтман (2003) Факты и загадки физики элементарных частиц. Всемирная научная издательская компания. ISBN 978-9812381491
Дж. П. Макэвой и Оскар Зарате (2004). Введение в квантовую теорию. Тотемные книги. ISBN 1840465778

внешние ссылки

"Микроскопический мир - Введение в квантовую механику ». Такада, Кендзиро, почетный профессор Университет Кюсю
Квантовая теория. на encyclopedia.com
Жуткий квант
Квантовый обмен (учебные пособия и учебное ПО с открытым исходным кодом).
Атомы и периодическая таблица
Одно- и двухщелевое взаимодействие
Временная эволюция волнового пакета в квадратной скважине Анимированная демонстрация дисперсии волнового пакета во времени.
Эксперименты с одиночными фотонами Введение в квантовую физику с интерактивными экспериментами
Кэрролл, Шон М. «Квантовая механика (смущение)». Шестьдесят символов. Брэди Харан для Ноттингемского университета.
Комплексные анимации
«Квантовая механика и структура атомов» на YouTube Настоящий урок физики начинается со 2:20 видео.

[5] Был создан ряд формул, которые могли описать некоторые экспериментальные измерения теплового излучения: как длина волны, на которой излучение наиболее сильно изменяется с температурой, определяется выражением Закон смещения Вина, общая мощность, излучаемая на единицу площади, определяется как Закон Стефана – Больцмана. Лучшим теоретическим объяснением экспериментальных результатов было Закон Рэлея – Джинса, что хорошо согласуется с экспериментальными результатами на больших длинах волн (или, что то же самое, низких частотах), но сильно не согласуется с короткими длинами волн (или высоких частот). Фактически, на коротких волнах классическая физика предсказывала, что энергия будет излучаться горячим телом с бесконечной скоростью. Этот явно неверный результат известен как ультрафиолетовая катастрофа.

[7] Слово квант исходит из Латинское слово для "сколько" (как и количество). То, что есть квантованный, как и энергия гармонических осцилляторов Планка, может принимать только определенные значения. Например, в большинстве стран деньги квантуются эффективно, а количество денег монета с наименьшей стоимостью в обращении. Механика - это отрасль науки, изучающая действие сил на объекты. Итак, квантовая механика - это часть механики, которая имеет дело с объектами, для которых квантованы определенные свойства.

[15] Фактически, могут быть эффекты, зависящие от интенсивности, но при интенсивностях, достижимых с помощью нелазерных источников, эти эффекты не наблюдаются.

[18] Уравнение фотоэлектрического эффекта Эйнштейна мочь быть выведенным и объясненным без требуя понятия «фотоны». То есть электромагнитное излучение можно рассматривать как классическую электромагнитную волну, если электроны в материале обрабатываются законами квантовой механики. Результаты количественно верны для тепловых источников света (солнце, лампы накаливания и т. Д.) Как по скорости эмиссии электронов, так и по их угловому распределению. Подробнее об этом см.^[14]

[21] Классическая модель атома называется планетарной, а иногда и планетарной. Модель Резерфорда -после Эрнест Резерфорд который предложил его в 1911 году на основе Эксперимент с золотой фольгой Гейгера – Марсдена, который впервые продемонстрировал существование ядра.

[26] В этом случае энергия электрона равна сумме его энергии. кинетический и потенциал энергии. Электрон имеет кинетическую энергию в силу своего фактического движения вокруг ядра и потенциальную энергию из-за своего электромагнитного взаимодействия с ядром.

[27] Модель может быть легко модифицирована для учета спектра излучения любой системы, состоящей из ядра и одного электрона (т. Е. ионы такие как он⁺ или O⁷⁺, которые содержат только один электрон), но не могут быть расширены до атома с двумя электронами, такого как нейтральный гелий.

[29] Электронная дифракция была впервые продемонстрирована через три года после того, как де Бройль опубликовал свою гипотезу. На Университет Абердина, Джордж Томсон пропускал пучок электронов через тонкую металлическую пленку и наблюдал дифракционные картины, как и предполагала гипотеза де Бройля. В Bell Labs, Дэвиссон и Germer направил электронный луч через кристаллическую решетку. Де Бройль был награжден Нобелевская премия по физике в 1929 г. за свою гипотезу; Томсон и Дэвиссон разделили Нобелевскую премию по физике в 1937 году за свои экспериментальные работы.

[42] Более сложный взгляд на то, как Гейзенберг перешел от старой квантовой теории и классической физики к новой квантовой механике, см. Путь Гейзенберга к матричной механике.

[1] "Квантовая механика". Национальное общественное радио. Получено 22 июн 2016.

[2] Кун, Томас С. Структура научных революций. Четвертое изд. Чикаго; Лондон: Издательство Чикагского университета, 2012. Печать.

[3] «Введение в квантовую механику». Socratease. Архивировано из оригинал 15 сентября 2017 г.

[4] Фейнман, Ричард П. (1988). КЭД: странная теория света и материи (1-й принстонский пбк., Седьмое издание с исправлениями. Ред.). Принстон, Нью-Джерси: Издательство Принстонского университета. стр.10. ISBN 978-0691024172.

[6] Этот результат был опубликован (на немецком языке) как Планк, Макс (1901). "Ueber das Gesetz der Energieverteilung im Normalspectrum" (PDF). Анна. Phys. 309 (3): 553–63. Bibcode:1901АнП ... 309..553П. Дои:10.1002 / andp.19013090310. Архивировано из оригинал (PDF) 10 июня 2012 г.. Английский перевод: «О законе распределения энергии в нормальном спектре». Архивировано из оригинал 18 апреля 2008 г.

[8] Фрэнсис Уэстон Сирс (1958). Механика, волновое движение и тепло. Эддисон-Уэсли. п. 537.

[9] "Нобелевская премия по физике 1918 г.". Нобелевский фонд. Получено 1 августа 2009.

[Kragh-10] Краг, Хельге (1 декабря 2000 г.). «Макс Планк: упорный революционер». PhysicsWorld.com.

[11] Эйнштейн, Альберт (1905). "Über einen die Erzeugung und Verwandlung des Lichtes betreffenden heuristischen Gesichtspunkt" (PDF). Annalen der Physik. 17 (6): 132–48. Bibcode:1905AnP ... 322..132E. Дои:10.1002 / andp.19053220607., переводится на английский как Об эвристической точке зрения на производство и преобразование света В архиве 11 июня 2009 г. Wayback Machine. Термин «фотон» был введен в 1926 году.

[12] «Возрождение волновой теории света в начале девятнадцатого века». www.encyclopedia.com. Получено 16 октября 2018.

[taylor_127-9-13] а ^б ^c ^d ^е Taylor, J. R .; Zafiratos, C.D .; Дубсон, М.А. (2004). Современная физика для ученых и инженеров. Прентис Холл. С. 127–29. ISBN 0135897890.

[Hawking-14] Хокинг, Стивен (2001). Вселенная в двух словах. Петух. ISBN 978-0553802023.

[16] Дике, Роберт Генри; Виттке, Джеймс П. (1960). Введение в квантовую механику. Издательство Эддисон-Уэсли. п. 12. ISBN 978-0201015102.

[17] Lamb, Willis E., Jr .; Скалли, Марлан О. «Фотоэлектрический эффект без фотонов» (PDF). NTRS.NASA.gov.

[19] Джим Лукас: «Что такое ультрафиолетовый свет?», 15 сентября 2017 г., livescience.com Доступ 27 декабря 2017 г.

[20] 'Два уравнения, управляющие поведением света: часть вторая E = hν' на сайте chemteam.info Доступ 27 декабря 2017 г.

[taylor_147-8-22] а ^б Taylor, J. R .; Zafiratos, C.D .; Дубсон, М.А. (2004). Современная физика для ученых и инженеров. Прентис Холл. С. 147–48. ISBN 0135897890.

[23] McEvoy, J. P .; Зарате, О. (2004). Введение в квантовую теорию. Тотемные книги. С. 70–89, [89]. ISBN 1840465778.

[WorldBook-24] Всемирная книжная энциклопедия, стр.6, 2007.^{[требуется полная цитата ]}

[25] Дике и Виттке, Введение в квантовую механику, п. 10f.

[28] McEvoy, J. P .; Зарате, О. (2004). Введение в квантовую теорию. Тотемные книги. С. 110 и далее. ISBN 1840465778.

[30] Акзель, Амир Д., Запутанность, стр. 51 и далее. (Пингвин, 2003) ISBN 978-1551926476

[31] McEvoy, J. P .; Зарате, О. (2004). Введение в квантовую теорию. Тотемные книги. п. 114. ISBN 1840465778.

[Zettili-32] Зеттили, Нуредин (2009). Квантовая механика: концепции и приложения. Джон Уайли и сыновья. С. 26–27. ISBN 978-0470026786.

[Selleri-33] Селлери, Франко (2012). Двойственность волны и частицы. Springer Science and Business Media. п. 41. ISBN 978-1461533320.

[Podgorsak-34] Подгорсак, Эрвин Б. (2013). Сборник по радиационной физике для медицинских физиков. Springer Science and Business Media. п. 88. ISBN 978-3642201868.

[Halliday&Resnick-35] Холлидей, Дэвид; Резник, Роберт (2013). Основы физики, 10-е изд.. Джон Уайли и сыновья. п. 1272. ISBN 978-1118230619.

[Myers-36] Майерс, Расти Л. (2006). Основы физики. Издательская группа «Гринвуд». стр.172. ISBN 0313328579. Принцип дополнительности волновой корпускулярный дуализм.

[ShamosGreatExperiments-37] а ^б Шамос, Моррис Х (1 января 1987 г.). Великие эксперименты в физике: отчеты из первых рук от Галилея до Эйнштейна. Курьерская корпорация. п. 108.

[38] Мерали, Зея (21 мая 2015 г.). «Квантовая физика: что на самом деле реально?». Природа. С. 278–80. Bibcode:2015Натура.521..278М. Дои:10.1038 / 521278a. Получено 7 января 2017.

[39] Эйбенбергер, Сандра (2013). «Материя – волна интерференции частиц, выбранных из молекулярной библиотеки с массами, превышающими 10 000 а.е.м.». Физическая химия Химическая физика. 15 (35): 14696–700. arXiv:1310.8343. Bibcode:2013PCCP ... 1514696E. Дои:10.1039 / C3CP51500A. PMID 23900710. S2CID 3944699. [I] В интерферометре с тремя решетками ... Мы наблюдаем высококонтрастные структуры квантовых полос молекул ... имеющих 810 атомов в одной частице.

[40] McEvoy, J. P .; Зарате, О. (2004). Введение в квантовую теорию. Тотемные книги. п. 87. ISBN 1840465778.

[Heisenberg1925-41] Ван дер Варден, Б. Л. (1967). Источники квантовой механики. Минеола, Нью-Йорк: Dover Publications. С. 261–76. Поступило 29 июля 1925 г. См. Статью Вернера Гейзенберга "Квантовая теоретическая переинтерпретация кинематических и механических соотношений", стр. 261–76.

[SchrBiog-43] Организация Нобелевской премии. "Эрвин Шредингер - Биографический". Получено 28 марта 2014. Его великое открытие - волновое уравнение Шредингера - было сделано в конце этой эпохи - в первой половине 1926 года.

[EB-SchrEquation-44] «Уравнение Шредингера (физика)», Британская энциклопедия

[45] Эрвин Шредингер, "Современная ситуация в квантовой механике", стр. 9. "Этот перевод был первоначально опубликован в Proceedings of the American Philosophical Society, 124, 323–388, а затем появился как Раздел I.11 Части I Квантовой теории и измерений (JA Wheeler and WH Zurek, eds., Princeton University Press, NJ 1983). Эту статью можно скачать здесь: Эрвин Шредингер. "Перевод статьи Шредингера" Кошачий парадокс."". Перевод Джона Д. Триммера. Архивировано из оригинал 13 ноября 2010 г.

[46] Гейзенберг, В. (1955). Развитие интерпретации квантовой теории, стр. 12–29 в Нильс Бор и развитие физики: очерки, посвященные Нильсу Бору по случаю его семидесятилетия, Отредактировано Паули, В. с помощью Розенфельд, Л. и Вайскопф, В., Пергамон, Лондон, стр. 13: «единичный квантовый скачок ... является фактическим по своей природе».

[47] В. Мур, Шредингер: жизнь и мысль, Cambridge University Press (1989), стр. 222. См. Стр. 227 по собственным словам Шредингера.

[nytimesQuantumJump-48] «Физики наконец-то увидят квантовый скачок собственными глазами». Нью-Йорк Таймс. Получено 30 ноября 2019.

[49] "Нобелевская премия по физике 1932 г.". NobelPrize.org.

[50] Гейзенберг впервые опубликовал свою работу о принципе неопределенности в ведущем немецком физическом журнале. Zeitschrift für Physik: Гейзенберг, В. (1927). "Über den anschaulichen Inhalt der quantentheoretischen Kinematik und Mechanik". Z. Phys. 43 (3–4): 172–98. Bibcode:1927ZPhy ... 43..172H. Дои:10.1007 / BF01397280. S2CID 122763326.

[51] "Нобелевская премия по физике 1932 г.". NobelPrize.org.

[EB-uncertainty-52] «Принцип неопределенности», Британская энциклопедия

[Pauling-53] а ^б ^c Полинг, Линус (1960). Природа химической связи (3-е изд.). Итака, Нью-Йорк: Издательство Корнельского университета. п.47. ISBN 0801403332. Получено 1 марта 2016.

[EB-orbital-54] «Орбиталь (химия и физика)», Британская энциклопедия

[55] Э. Шредингер, Труды Кембриджского философского общества, 31 (1935), с. 555, говорит: «Когда две системы, состояния которых мы знаем по их соответствующему представлению, вступают во временное физическое взаимодействие из-за известных сил между ними, и когда после некоторого времени взаимного влияния системы снова разделяются, тогда они больше не могут можно описать так же, как и раньше, а именно, наделив каждого из них своим собственным представителем. Я бы не назвал это один скорее то характерная черта квантовой механики ».

[56] Дэвид Кайзер, Реальна ли квантовая запутанность?, The New York Times, ноябрь 2014 г.

[57] Джон Г. Крамер. «Квантовая нелокальность и возможность сверхсветовых эффектов». npl.washington.edu. Архивировано из оригинал 29 декабря 2010 г.

[58] «Механика», Онлайн-словарь Merriam-Webster

[EB-field-59] "Поле", Британская энциклопедия

[Hammond-60] Ричард Хаммонд, Неизвестная Вселенная, New Page Books, 2008. ISBN 978-1601630032

[61] «Избранные физики - Поль Дирак 1902–1984». www.physicalworld.org.

[nobel-62] «Нобелевская премия по физике 1933 года». Нобелевский фонд. Получено 24 ноября 2007.

[63] «Обменные частицы». hyperphysics.phy-astr.gsu.edu. Получено 16 октября 2018.

[64] «Десять лет открытий Большого адронного коллайдера под швейцарской сельской местностью - это только начало расшифровки Вселенной». www.thelocal.ch. 5 октября 2018 г.. Получено 16 октября 2018.

[65] "Копенгагенская интерпретация". abyss.uoregon.edu. Получено 16 октября 2018.

[66] Дуррани, З. А. К .; Ахмед, Х. (2008). Виджай Кумар (ред.). Нанокремний. Эльзевир. п. 345. ISBN 978-0080445281.

[1]

[2]

[3]

[4]

[примечание 1]

[5]

[заметка 2]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[заметка 3]

[13]

[примечание 4]

[15]

[16]

[примечание 5]

[17]

[18]

[19]

[20]

[примечание 6]

[примечание 7]

[21]

[примечание 8]

[22]

[23]

[24]

[25]

[26]

[27]

[28]

[29]

[30]

[31]

[32]

[33]

[примечание 9]

[34]

[35]

[36]

[37]

[38]

[39]

[40]

[41]

[42]

[43]

[44]

[45]

[46]

[47]

[48]

[49]

[50]

[51]

[52]

[53]

[54]

[55]

[56]

[57]

[14]

Электронная конфигурация
Электронная оболочка Атомная орбиталь Квантовая механика Введение в квантовую механику
Квантовые числа	Главное квантовое число ( $п$ ) Азимутальное квантовое число ( $ℓ$ ) Магнитное квантовое число ( $м$ ) Спиновое квантовое число ( $s$ )
Конфигурации основного состояния	Периодическая таблица (электронные конфигурации) Электронные конфигурации элементов (страница данных)
Электронное наполнение	Принцип исключения Паули Правило Хунда Принцип Ауфбау
Электронное спаривание	Электронная пара Неспаренный электрон
Связующее участие	валентный электрон Основной электрон
Подсчет электронов правила	Правило октета 18-электронное правило