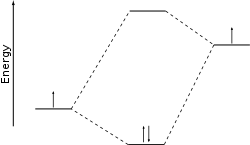
Линейная комбинация атомных орбиталей - Linear combination of atomic orbitals
А линейная комбинация атомных орбиталей или ЛКАО это квантовая суперпозиция из атомные орбитали и методика расчета молекулярные орбитали в квантовая химия.[1] В квантовой механике электронные конфигурации атомов описываются как волновые функции. В математическом смысле эти волновые функции являются базисный набор функций, базисных функций, которые описывают электроны данного атома. В химические реакции, орбитальные волновые функции изменяются, т.е. электронное облако форма меняется в зависимости от типа атомов, участвующих в химическая связь.
Он был введен в 1929 году сэром Джон Леннард-Джонс с описанием связи в двухатомных молекулах первого главного ряда периодической таблицы, но ранее использовался Линус Полинг для ч2+.[2][3]
Далее следует математическое описание.
Первоначальное предположение состоит в том, что количество молекулярных орбиталей равно количеству атомных орбиталей, включенных в линейное расширение. В некотором смысле n атомных орбиталей объединяются, образуя n молекулярных орбиталей, которые можно пронумеровать я = От 1 до n и не все могут быть одинаковыми. Выражение (линейное разложение) для я -я молекулярная орбиталь будет:
или
где молекулярная орбиталь, представленная как сумма n атомные орбитали , каждый из которых умножается на соответствующий коэффициент , и р (пронумерованные от 1 до n) обозначают, какая атомная орбиталь объединена в этом термине. Коэффициенты представляют собой веса вкладов n атомных орбиталей в молекулярную орбиталь. В Хартри – Фок процедура используется для получения коэффициентов разложения.
Таким образом, орбитали выражаются как линейные комбинации из базисные функции, а базисные функции однозначны.электрон функции, которые могут или не могут быть сосредоточены на ядра компонента атомы из молекула. В любом случае базисные функции обычно также называют атомарными орбиталями (хотя только в первом случае это название кажется адекватным). Обычно используются атомные орбитали водородоподобные атомы поскольку они известны аналитически, т.е. Орбитали слейтеровского типа но возможны и другие варианты, например Гауссовы функции из стандартных базисов или псевдоатомных орбиталей из плоских волновых псевдопотенциалов.
Путем минимизации общего энергия системы, соответствующий набор коэффициенты линейных комбинаций. Этот количественный подход теперь известен как Метод Хартри – Фока. Однако, поскольку разработка вычислительная химия, метод LCAO часто относится не к реальной оптимизации волновой функции, а к качественному обсуждению, которое очень полезно для прогнозирования и обоснования результатов, полученных с помощью более современных методов. В этом случае форма молекулярных орбиталей и их соответствующие энергии рассчитываются приблизительно из сравнения энергий атомных орбиталей отдельных атомов (или молекулярных фрагментов) и применения некоторых рецептов, известных как уровень отталкивания и тому подобное. Графики, построенные для более ясного обсуждения, называются диаграммы корреляции. Требуемые атомные орбитальные энергии могут быть получены из расчетов или непосредственно из эксперимента через Теорема Купманса.
Это достигается за счет использования симметрии молекул и орбиталей, участвующих в связывании, и поэтому иногда называется симметрично адаптированной линейной комбинацией (SALC). Первым шагом в этом процессе является присвоение точечная группа к молекуле. Типичный пример - вода, которая имеет C2v симметрия. Потом сводимое представление склеивания показано ниже для воды:
Каждая операция в точечной группе выполняется над молекулой. Количество неподвижных облигаций является характером этой операции. Это приводимое представление раскладывается в сумму неприводимых представлений. Эти неприводимые представления соответствуют симметрии задействованных орбиталей.
Диаграммы МО обеспечить простую качественную обработку ЛКАО.
Количественные теории - это Метод Хюккеля, то расширенный метод Хюккеля и Метод Паризера – Парра – Попла.
Смотрите также
- Компьютерные программы по квантовой химии
- Метод Хартри – Фока
- Базовый набор (химия)
- Плотный переплет
- Метод голштинской селедки
внешняя ссылка
- ЛКАО @ chemistry.umeche.maine.edu Связь
Рекомендации
- ^ Хухи, Джеймс. Неорганическая химия: принципы строения и реакционной способности
- ^ Фридрих Хунд и химия, Вернер Куцельнигг, по случаю 100-летия Хунда, Angewandte Chemie, 35, 572–586, (1996), Дои: 10.1002 / anie.199605721
- ^ Роберт С. Малликен Нобелевская лекция, Наука, 157, вып. 3784, 13 - 24, (1967)