Зарядить кубит - Charge qubit
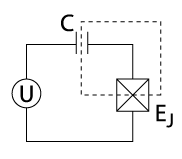
В квантовые вычисления, а зарядить кубит (также известен как Коробка с купер-парой) это кубит чья основа состояния находятся обвинять состояния (например, состояния, которые представляют наличие или отсутствие лишних Куперовские пары на острове).[1][2][3] В сверхпроводящие квантовые вычисления, зарядовый кубит[4] формируется крошечным сверхпроводящий остров в сочетании с Джозефсоновский переход (или практически, сверхпроводящий туннельный переход ) в сверхпроводящий резервуар (см. рисунок). Состояние кубита определяется количеством куперовских пар, которые прошли туннель через соединение. В отличие от зарядового состояния атомарного или молекулярного иона, зарядовые состояния такого «островка» включают макроскопическое количество электронов проводимости острова. Квантовая суперпозиция зарядовых состояний может быть достигнута путем настройки напряжения затвора. U который контролирует химический потенциал острова. Зарядный кубит обычно считывается электростатическим соединением острова с чрезвычайно чувствительным электрометр такой как радиочастота одноэлектронный транзистор.
Типичный Т2 время согласованности для зарядового кубита порядка 1–2 мкс.[5] Недавние работы показали Т2 время приближается к 100 мкс при использовании зарядового кубита, известного как трансмон внутри трехмерного сверхпроводящего резонатора.[6][7] Понимание ограничений Т2 является активной областью исследований в области сверхпроводящие квантовые вычисления.
Изготовление
Зарядные кубиты изготавливаются с использованием техник, аналогичных тем, которые используются для микроэлектроника. Обычно устройства изготавливаются на кремниевых или сапфировых пластинах с использованием электронно-лучевая литография (отличается от фазовый кубит, который использует фотолитография ) и процессы испарения металлических тонких пленок. Создавать Джозефсоновские переходы, техника, известная как теневое испарение обычно используется; это включает в себя испарение исходного металла поочередно под двумя углами через литографическую маску в резисте электронного луча. Это приводит к двум перекрывающимся слоям сверхпроводящего металла, между которыми располагается тонкий слой изолятора (обычно оксид алюминия ) депонируется.
Гамильтониан
Если переход Джозефсона имеет емкость перехода , а затворный конденсатор , то зарядовая (кулоновская) энергия одной куперовской пары равна:
Если обозначает количество избыточных куперовских пар на острове (т.е. его чистый заряд равен ), то гамильтониан будет:[4]
куда - управляющий параметр, известный как эффективный компенсационный заряд ( напряжение затвора), а джозефсоновская энергия туннельного перехода.
При низкой температуре и низком напряжении на затворе можно ограничить анализ только самым низким и состояний, и, следовательно, получить двухуровневую квантовую систему (также известную как кубит ).
Обратите внимание, что некоторые недавние статьи[8][9] примите другие обозначения и определите энергию заряда как энергию одного электрона:
и тогда соответствующий гамильтониан:
Преимущества
На сегодняшний день наиболее успешными реализациями кубитов являются: ионные ловушки и ЯМР, с Алгоритм Шора даже реализуется с использованием ЯМР.[10] Однако трудно представить, что эти два метода можно масштабировать до сотен, тысяч или миллионов кубитов, необходимых для создания квантовый компьютер. Твердое состояние представления кубитов намного легче масштабируются, но сами они имеют свою проблему: декогеренция. Однако преимущество сверхпроводников состоит в том, что их легче масштабировать, и они более когерентны, чем обычные твердотельные системы.[10]
Экспериментальный прогресс
Сверхпроводящие зарядовые кубиты быстро развиваются. Впервые они были предложены в 1997 году Шнирманом,[11] а к 2001 г. наблюдались когерентные колебания.
Рекомендации
- ^ В. Бушиат, Д. Вион, П. Джойез, Д. Эстев и М. Х. Деворет, «Квантовая когерентность с одной куперовской парой», Physica Scripta T76, 165-170 (1998), Дои:10.1238 / Physica.Topical.076a00165
- ^ Ю. Накамура, Ю. А. Пашкин и Дж. С. Цай, "Когерентное управление макроскопическими квантовыми состояниями в ящике с одной куперовской парой", Природа 398, 786-788 (1999), Дои:10.1038/19718, arXiv: 9904003
- ^ К. В. Ленерт, Б. А. Турек, К. Блад, Л. Ф. Шпиц, Д. Гуннарссон, П. Делсинг и Р. Дж. Шелькопф, "Измерение времени жизни возбужденного состояния микроэлектронной схемы", Phys. Rev. Lett. 90, 027002 (2003), Дои:10.1103 / PhysRevLett.90.027002
- ^ а б Махлин, Юрий; Шен, Герд; Шнирман, Александр (2001-05-08). «Квантовая государственная инженерия с устройствами на джозефсоновском переходе». Обзоры современной физики. 73 (2): 357–400. arXiv:cond-mat / 0011269. Bibcode:2001РвМП ... 73..357М. Дои:10.1103 / RevModPhys.73.357. ISSN 0034-6861.
- ^ А.А. Houck и другие., «Жизнь после шума заряда: недавние результаты с трансмонными кубитами», Quant. Инф. Proc. 8, 105 (2009), Дои:10.1007 / s11128-009-0100-6, arXiv: 0812.1865
- ^ Х. Пайк и другие., "Наблюдение высокой когерентности в кубитах джозефсоновских переходов, измеренных в трехмерной схеме QED-архитектуры", Phys. Rev. Lett. 107, 240501 (2011), Дои:10.1103 / PhysRevLett.107.240501, arXiv: 1105.4652
- ^ К. Ригетти и другие., «Сверхпроводящий кубит в волноводном резонаторе с временем когерентности, приближающимся к 0,1 мс», arXiv: 1202.5533 (2012)
- ^ Дидье, Николя; Sete, Eyob A .; да Силва, Маркус П .; Ригетти, Чад (23 февраля 2018 г.). «Аналитическое моделирование параметрически-модулированных кубитов трансмона». Физический обзор A. 97 (2): 022330. arXiv:1706.06566. Bibcode:2018PhRvA..97b2330D. Дои:10.1103 / PhysRevA.97.022330. ISSN 2469-9926.
- ^ Schreier, J. A .; Houck, A. A .; Кох, Йенс; Schuster, D. I .; Johnson, B.R .; Chow, J.M .; Gambetta, J.M .; Majer, J .; Frunzio, L .; Devoret, M. H .; Гирвин, С. М. (2008-05-12). «Подавление декогеренции зарядового шума в сверхпроводящих зарядовых кубитах». Физический обзор B. 77 (18): 180502. arXiv:0712.3581. Bibcode:2008PhRvB..77r0502S. Дои:10.1103 / PhysRevB.77.180502. ISSN 1098-0121.
- ^ а б Кубиты сверхпроводящего заряда, Дензил Энтони Родригес, стр. 3
- ^ Шнирман, Александр; Шен, Герд; Хермон, Зив (22 сентября 1997 г.). «Квантовые манипуляции с малыми переходами Джозефсона». Письма с физическими проверками. 79 (12): 2371–2374. arXiv:cond-mat / 9706016. Bibcode:1997ПхРвЛ..79.2371С. Дои:10.1103 / Physrevlett.79.2371. ISSN 0031-9007.






![{ displaystyle H = sum _ {n} { big [} E _ { rm {C}} (n-n _ { rm {g}}) ^ {2} | n rangle langle n | - { frac {1} {2}} E _ { rm {J}} (| n rangle langle n + 1 | + | n + 1 rangle langle n |) { big]},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f30900c7e806d9ef2845a74f9002f8e5a007f0c8)






![{ displaystyle H = sum _ {n} { big [} 4E _ { rm {C}} (n-n _ { rm {g}}) ^ {2} | n rangle langle n | - { frac {1} {2}} E _ { rm {J}} (| n rangle langle n + 1 | + | n + 1 rangle langle n |) { big]}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/087ead1ff3d84254a8c2f820034493c161617b64)
