L10a140 ссылка - L10a140 link

L10a140
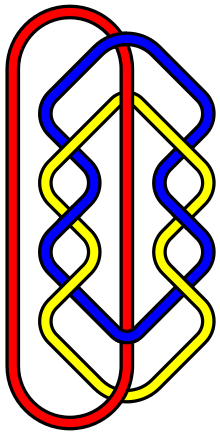Длина тесьмы	10
Тесьма нет.	3
Переход нет.	10
Гиперболический объем	12.27627758
Обозначение Конвея	[.3:30]
Thistlethwaite	L10a140
Другой
чередование

в математическая теория узлов, L10a140 это имя в Таблица ссылок Thistlethwaite из связь из трех петель, который имеет десять пересечений между петлями, когда он представлен в простейшей визуальной форме.^[1] Это интересно, потому что это, по-видимому, простейшее звено, имеющее Бруннская недвижимость - связь связанных компонентов, которая при удалении одного компонента становится полностью несоединенной^[2] - кроме шестикросс Кольца Борромео.^[3]

Другими словами, нет двух петель. напрямую связаны друг с другом, но все три вместе взаимосвязаны, поэтому удаление любого цикла освобождает два других. На изображении в информационном окне справа красная петля не связана ни с синей, ни с желтой петлями, а если красная петля удалена, то синюю и желтую петли также можно отделить друг от друга, не разрезая ни одну из них.

Согласно работе Славика В. Джаблана, звено L10a140 можно рассматривать как второе в бесконечной серии брунновских звеньев, начинающихся с колец Борромео. Итак, если синяя и желтая петли имеют только один виток с каждой стороны, в результате получается конфигурация колец Борромео; если синяя и желтая петли имеют по три витка с каждой стороны, результирующая конфигурация представляет собой звено L10a140; если синяя и желтая петли имеют по пять витков с каждой стороны, в результате получается трехпетлевое звено с 14 общими перекрестками и т. д.^[4]

Инварианты

В многомерный полином Александера для L10a140 ссылка есть

${\displaystyle \Delta (u,v,w)={\frac {(u-1)(v-1)(w-1)(vw+1)^{2}}{vw{\sqrt {uvw}}}},\,}$

то Многочлен Конвея является

${\displaystyle \nabla (z)=4z^{4}+4z^{6}+z^{8},\,}$

то Многочлен Джонса факторы хорошо как

${\displaystyle {\begin{aligned}V(t)&=-t^{5}+3t^{4}-5t^{3}+8t^{2}-9t+12-9t^{-1}+8t^{-2}-5t^{-3}+3t^{-4}-t^{-5}\\[8pt]&=-{\frac {1}{t^{5}}}\left(t^{5}-2t^{4}+t^{3}-2t^{2}+t-1\right)\left(t^{5}-t^{4}+2t^{3}-t^{2}+2t-1\right)\\[8pt]&=w(t)w(1/t),\,\end{aligned}}}$

куда ${\displaystyle w(t)=t^{5}-2t^{4}+t^{3}-2t^{2}+t-1.}$ (Заметь ${\displaystyle w(t)}$ по сути является полиномом Джонса для Ссылка Уайтхеда.)

В Полином ХОМФЛИ является

${\displaystyle P(\alpha ,z)=z^{-2}\alpha ^{-2}-4z^{2}\alpha ^{-2}-4z^{4}\alpha ^{-2}-z^{6}\alpha ^{-2}-2z^{-2}+8z^{2}+12z^{4}+6z^{6}+z^{8}+z^{-2}\alpha ^{2}-4z^{2}\alpha ^{2}-4z^{4}\alpha ^{2}-z^{6}\alpha ^{2},\,}$

и Многочлен Кауфмана является

${\displaystyle {\begin{aligned}F(a,z)&=1+2z^{-2}+a^{-2}z^{-2}+a^{2}z^{-2}-2a^{-1}z^{-1}-az^{-1}-20z^{2}+2a^{-4}z^{2}\\[6pt]&{}-8a^{-2}z^{2}-8a^{2}z^{2}+2a^{4}z^{4}+2a^{4}z^{2}-2a^{-5}z^{3}+4a^{-3}z^{3}+6a^{-1}z^{3}\\[6pt]&{}+6az^{3}+4a^{3}z^{3}-2a^{5}z^{3}+42z^{4}-7a^{-4}z^{4}+14a^{-2}z^{4}\\[6pt]&{}+14a^{2}z^{4}-7a^{4}z^{4}+a^{-5}z^{5}-9a^{-3}z^{5}-2a^{-1}z^{5}-2az^{5}-9a^{3}z^{5}\\[6pt]&{}+a^{5}z^{5}-28z^{6}+3a^{-4}z^{6}-11a^{-2}z^{6}-11a^{2}z^{6}+3a^{4}z^{6}+4a^{-3}z^{7}\\[6pt]&{}-2a^{-1}z^{7}-2az^{7}+4a^{3}z^{7}+8z^{8}+4a^{-2}z^{8}+4a^{2}z^{8}+2a^{-1}z^{9}+2az^{9}.\end{aligned}}}$

Псевдосимметричные визуальные варианты

Дэвид Сварт,^[5] и независимо друг от друга Рик Мабри и Лора МакКормик,^[6] обнаружили альтернативные 12-пересекающиеся визуальные репрезентации связи L10a140. На этих изображениях звено больше не имеет строго чередующихся пересечений (как в его простейшей форме с 10 пересечениями), но имеет большую поверхностную симметрию.

Итак, крайнее левое изображение ниже показывает звено с 12 пересечениями (отличное как от колец Борромео, так и звена L10a140) с шестикратной вращательной симметрией. На центральном изображении показано похожее изображение звена L10a140 (но без истинной симметрии вращения). Точно так же крайнее правое изображение показывает изображение звена L10a140 с поверхностной четырехкратной симметрией.

• 

  Полностью симметричное брунновское звено с 12 пересечениями (L12a1882)

• 

  L10a140 в псевдо 6-симметричной форме

• 

  L10a140 в псевдо 4-симметричной форме

Рекомендации

1. "L10a140 ", Узел Атлас.
2. Адамс, Колин С. (1994). Книга узлов,^{[страница нужна ]}. Американское математическое общество. ISBN  9780716723936.
3. Бар-Натан, Дрор (2010-08-16). "Все бруннианцы, может быть ", Академический Омут.
4. Джаблан, Славик В., Ссылки Борромео настолько редки?, Форма 14 (1999), 269–277. Онлайн в электронном журнале Висмат. L10a140 изображен на среднем рисунке верхнего изображения.
5. Дрор Бар-Натан (14.08.2010). "Ссылка от Дэвида Сварта ", [Академический Омут].
6. Сварт, Дэвид (апрель 2011 г.). "Что есть, то есть". Математические горизонты. 18 (4).

внешняя ссылка

• "Что есть, то есть", Flickr.com.