Присоединенные функторы - Adjoint functors

По поводу построения в теории поля см. Адъюнкция (теория поля). Для построения в топологии см. Прилегающее пространство.

В математика в частности теория категорий, примыкание это отношения двух функторы можно иметь. Два функтора, стоящие в этой связи, известны как присоединенные функторы, один из левый смежный а другой правый смежный. Пары сопряженных функторов встречаются в математике повсеместно и часто возникают в результате построения «оптимальных решений» определенных проблем (т. Е. Конструкций объектов, имеющих определенное универсальная собственность ), например, построение бесплатная группа на съемочной площадке в алгебре, или построение Каменно-чешская компактификация из топологическое пространство в топологии.

По определению, связь между категориями C и D пара функторов (предполагается, что ковариантный )

${\displaystyle F:{\mathcal {D}}\rightarrow {\mathcal {C}}}$ и ${\displaystyle G:{\mathcal {C}}\rightarrow {\mathcal {D}}}$

и для всех объектов Икс в C и Y в D а биекция между соответствующими множествами морфизма

${\displaystyle \mathrm {hom} _{\mathcal {C}}(FY,X)\cong \mathrm {hom} _{\mathcal {D}}(Y,GX)}$

такое, что это семейство биекций естественный в Икс и Y. Естественность здесь означает наличие естественных изоморфизмов между парой функторов ${\displaystyle {\mathcal {C}}(F-,X):{\mathcal {D}}\to \mathrm {Set} }$ и ${\displaystyle {\mathcal {D}}(-,GX):{\mathcal {D}}\to \mathrm {Set} }$ для фиксированного Икс в C, а также пара функторов ${\displaystyle {\mathcal {C}}(FY,-):{\mathcal {C}}\to \mathrm {Set} }$ и ${\displaystyle {\mathcal {D}}(Y,G-):{\mathcal {C}}\to \mathrm {Set} }$ для фиксированного Y в D.

Функтор F называется левый сопряженный функтор или слева примыкает к г, в то время как г называется правый сопряженный функтор или прямо примыкает к F.

Примыкание категорий C и D несколько сродни "слабой форме" эквивалентность между C и D, и действительно, каждая эквивалентность является присоединением. Во многих ситуациях присоединение может быть «улучшено» до эквивалентности путем подходящей естественной модификации задействованных категорий и функторов.

Терминология и обозначения

Два разных корни используются: «добавочный» и «сопряженный». В более коротком Оксфордском словаре английского языка «адъюнкт» - от латинского, «сопряженный» - от французского.

В Mac Lane, Категории для работающего математика, глава 4, «Примыкающие», можно убедиться в следующем использовании. Учитывая семью

${\displaystyle \varphi _{XY}:\mathrm {hom} _{\mathcal {C}}(FY,X)\cong \mathrm {hom} _{\mathcal {D}}(Y,GX)}$

биекций гом-множеств мы называем ${\displaystyle \varphi }$ "примыкание" или "примыкание" между ${\displaystyle F}$ и ${\displaystyle G}$". Если ${\displaystyle f}$ стрелка в ${\displaystyle \mathrm {hom} _{\mathcal {C}}(FY,X)}$, ${\displaystyle \varphi f}$ является правильным "дополнением" ${\displaystyle f}$ (стр.81). Функтор ${\displaystyle F}$ остается "примыкающим" к ${\displaystyle G}$, и ${\displaystyle G}$ прямо примыкает к ${\displaystyle F}$. (Обратите внимание, что г может иметь собственное правое соединение, которое сильно отличается от F; см. ниже пример.)

В общем, фразы "${\displaystyle F}$ является левым сопряженным "и"${\displaystyle F}$ имеет правый сопряженный "эквивалентны.

Если F слева примыкает к г, мы также пишем

${\displaystyle F\dashv G.}$

Терминология взята из Гильбертово пространство Идея сопряженные операторы Т, U с участием ${\displaystyle \langle Ty,x\rangle =\langle y,Ux\rangle }$, которое формально аналогично приведенному выше соотношению между hom-множествами. Аналогия с присоединенными отображениями гильбертовых пространств может быть уточнена в определенных контекстах.^[1]

Введение и мотивация

Девиз: «Присоединенные функторы возникают везде».

— Сондерс Мак Лейн, Категории для рабочего математика

В длинный список примеров В этой статье указывается, что общие математические конструкции очень часто являются сопряженными функторами. Следовательно, общие теоремы о сопряженных функторах слева и справа содержат в себе детали многих полезных и в остальном нетривиальных результатов. Такие общие теоремы включают в себя эквивалентность различных определений присоединенных функторов, единственность правого сопряженного для данного левого сопряженного, тот факт, что левый / правый сопряженные функторы соответственно сохраняют коллимиты / пределы (которые также можно найти во всех областях математики), а также общие теоремы о сопряженных функторах, дающие условия, при которых данный функтор является сопряженным слева / справа.

Решения проблем оптимизации

В некотором смысле присоединенный функтор - это способ дать Наиболее эффективным решение некоторой проблемы с помощью метода, который шаблонный. Например, элементарная задача в теория колец как превратить rng (которое похоже на кольцо, которое может не иметь мультипликативной идентичности) в кольцо. В Наиболее эффективным Способ состоит в том, чтобы присоединить элемент '1' к rng, присоединить все (и только) элементы, которые необходимы для выполнения аксиом кольца (например, р+1 за каждый р в кольце) и не навязывают во вновь образованном кольце никаких отношений, не навязанных аксиомами. Более того, эта конструкция шаблонный в том смысле, что он работает по существу одинаково для любой группы.

Это довольно расплывчато, хотя и наводит на размышления, и его можно уточнить на языке теории категорий: конструкция Наиболее эффективным если он удовлетворяет универсальная собственность, и является шаблонный если он определяет функтор. Универсальные свойства бывают двух типов: начальные свойства и конечные свойства. Поскольку это двойной понятий, необходимо обсудить только одно из них.

Идея использования начального свойства заключается в постановке задачи в терминах некоторой вспомогательной категории. E, так что рассматриваемая задача соответствует поиску исходный объект из E. Это имеет то преимущество, что оптимизация- ощущение, что процесс находит Наиболее эффективным решение - означает что-то строгое и узнаваемое, скорее как достижение супремум. Категория E также является формульным в этой конструкции, так как это всегда категория элементов функтора, к которой строится присоединенный.

Вернемся к нашему примеру: возьмем данный rng р, и сделайте категорию E чья объекты являются rng гомоморфизмами р → S, с участием S кольцо, имеющее мультипликативную идентичность. В морфизмы в E между р → S₁ и р → S₂ находятся коммутативные треугольники формы (р → S₁, р → S₂, S₁ → S₂) где S₁ → S₂ является кольцевым отображением (сохраняющим тождество). (Обратите внимание, что это в точности определение категория запятой из р над включением унитарных колец в rng.) Существование морфизма между р → S₁ и р → S₂ подразумевает, что S₁ по крайней мере столь же эффективное решение, как S₂ к нашей проблеме: S₂ может иметь больше смежных элементов и / или больше отношений, не навязанных аксиомами, чем S₁Следовательно, утверждение, что объект р → Р* начальный в E, то есть существует морфизм от него к любому другому элементу E, означает, что кольцо р* это Наиболее эффективным решение нашей проблемы.

Два факта, что этот метод превращения RNG в кольца является Наиболее эффективным и шаблонный можно выразить одновременно, сказав, что он определяет присоединенный функтор. Более подробно: пусть F обозначают описанный выше процесс присоединения тождества к цепочке, так что F(р)=Р*. Позволять г обозначают процесс «забвения» того, что кольцо S имеет личность и рассматривает его просто как звено, поэтому по существу г(S)=S. потом F это левый сопряженный функтор из г.

Однако обратите внимание, что мы на самом деле не построили Р* еще; это важный и не совсем тривиальный алгебраический факт, что такой левый сопряженный функтор р → Р* действительно существует.

Симметрия задач оптимизации

Также возможно Начните с функтором F, и задайте следующий (неопределенный) вопрос: есть ли проблема, для которой F самое эффективное решение?

Представление о том, что F это самое эффективное решение к проблеме, поставленной г в определенном строгом смысле эквивалентно понятию, что г ставит самая сложная проблема это F решает.

Это дает интуицию того факта, что сопряженные функторы встречаются парами: если F слева примыкает к г, тогда г прямо примыкает к F.

Формальные определения

Существуют различные эквивалентные определения сопряженных функторов:

• Определения с помощью универсальных морфизмов легко сформулировать и требуют минимальных проверок при построении присоединенного функтора или доказательстве того, что два функтора сопряжены. Они также наиболее похожи на нашу интуицию, связанную с оптимизацией.
• Определение через hom-множества делает симметрию наиболее очевидной и является причиной использования слова прилегающий.
• Определение через присоединение коединиц удобно для доказательств о функторах, которые, как известно, являются сопряженными, поскольку они предоставляют формулы, которыми можно напрямую манипулировать.

Эквивалентность этих определений весьма полезна. Присоединенные функторы возникают везде, во всех областях математики. Поскольку структура в любом из этих определений порождает структуры в других, переключение между ними подразумевает использование большого количества утомительных деталей, которые в противном случае пришлось бы повторять отдельно в каждой предметной области.

Конвенции

Теория сопряженных имеет термины осталось и правильно в его основе, и есть много компонентов, которые находятся в одной из двух категорий C и D которые находятся на рассмотрении. Поэтому может быть полезно выбирать буквы в алфавитном порядке в зависимости от того, относятся ли они к категории «левосторонних». C или "правая" категория D, а также записывать их по возможности в этом порядке.

Например, в этой статье буквы Икс, F, ж, ε будет последовательно обозначать вещи, которые находятся в категории C, письма Y, г, г, η будет последовательно обозначать вещи, которые находятся в категории D, и по возможности на такие вещи будут ссылаться в порядке слева направо (функтор F : D → C можно рассматривать как «живущее» там, где находятся его выходы, в C).

Определение через универсальные морфизмы

По определению функтор ${\displaystyle F:D\to C}$ это левый сопряженный функтор если для каждого объекта ${\displaystyle X}$ в ${\displaystyle C}$ существует универсальный морфизм от ${\displaystyle F}$ к ${\displaystyle X}$. Прописано, это означает, что для каждого объекта ${\displaystyle X}$ в ${\displaystyle C}$ существует объект ${\displaystyle G(X)}$ в ${\displaystyle D}$ и морфизм ${\displaystyle \epsilon _{X}:F(G(X))\to X}$ так что для каждого объекта ${\displaystyle Y}$ в ${\displaystyle D}$ и каждый морфизм ${\displaystyle f:F(Y)\to X}$ существует уникальный морфизм ${\displaystyle g:Y\to G(X)}$ с участием ${\displaystyle \epsilon _{X}\circ F(g)=f}$.

Последнее уравнение выражается следующим коммутативная диаграмма:

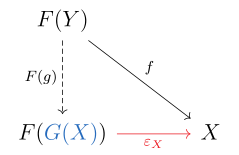
В этой ситуации можно показать, что ${\displaystyle G}$ можно превратить в функтор ${\displaystyle G:C\to D}$ уникальным образом, так что ${\displaystyle \epsilon _{X}\circ F(G(f))=f\circ \epsilon _{X'}}$ для всех морфизмов ${\displaystyle f:X'\to X}$ в ${\displaystyle C}$; ${\displaystyle F}$ тогда называется левый смежный к ${\displaystyle G}$.

Аналогично мы можем определить правосопряженные функторы. Функтор ${\displaystyle G:C\to D}$ это правый сопряженный функтор если для каждого объекта ${\displaystyle Y}$ в ${\displaystyle D}$, существует универсальный морфизм от ${\displaystyle Y}$ к ${\displaystyle G}$. Прописано, это означает, что для каждого объекта ${\displaystyle Y}$ в ${\displaystyle D}$, существует объект ${\displaystyle F(Y)}$ в ${\displaystyle C}$ и морфизм ${\displaystyle \eta _{Y}:Y\to G(F(Y))}$ так что для каждого объекта ${\displaystyle X}$ в ${\displaystyle C}$ и каждый морфизм ${\displaystyle g:Y\to G(X)}$ существует уникальный морфизм ${\displaystyle f:F(Y)\to X}$ с участием ${\displaystyle G(f)\circ \eta _{Y}=g}$.

Опять же, это ${\displaystyle F}$ можно однозначно превратить в функтор ${\displaystyle F:D\to C}$ такой, что ${\displaystyle G(F(g))\circ \eta _{Y}=\eta _{Y'}\circ g}$ для ${\displaystyle g:Y\to Y'}$ морфизм в ${\displaystyle D}$; ${\displaystyle G}$ тогда называется правый смежный к ${\displaystyle F}$.

Верно, как следует из терминологии, что ${\displaystyle F}$ слева примыкает к ${\displaystyle G}$ если и только если ${\displaystyle G}$ прямо примыкает к ${\displaystyle F}$.

Эти определения через универсальные морфизмы часто полезны для установления того, что данный функтор является левым или правым сопряженным, поскольку они минималистичны по своим требованиям. Они также интуитивно значимы в том смысле, что поиск универсального морфизма похож на решение проблемы оптимизации.

Определение через присоединение Hom-множества

А домашний набор примыкание между двумя категориями C и D состоит из двух функторы F : D → C и г : C → D и естественный изоморфизм

${\displaystyle \Phi :\mathrm {hom} _{C}(F-,-)\to \mathrm {hom} _{D}(-,G-)}$.

Это указывает на семейство биекций

${\displaystyle \Phi _{Y,X}:\mathrm {hom} _{C}(FY,X)\to \mathrm {hom} _{D}(Y,GX)}$

для всех объектов Икс в C и Y в D.

В этой ситуации, F слева примыкает к г и г прямо примыкает к F.

Это определение является логическим компромиссом в том смысле, что удовлетворить его несколько сложнее, чем определения универсального морфизма, и оно имеет меньше непосредственных последствий, чем определение единицы единицы. Это полезно из-за своей очевидной симметрии и как ступенька между другими определениями.

Чтобы интерпретировать Φ как естественный изоморфизм, нужно признать хом_C(F–, –) и хом_D(–, г–) как функторы. Фактически, они оба бифункторы от D^op × C к Набор (в категория наборов ). Подробнее читайте в статье о хом функторы. Явно естественность Φ означает, что для всех морфизмы ж : Икс → ИКС' в C и все морфизмы г : Y′ → Y в D следующая диаграмма ездит на работу:

Вертикальные стрелки на этой диаграмме - это стрелки, созданные композицией. Формально Hom (Fg, ж): Hom_C(FY, Икс) → Hom_C(FY ′, ИКС') дан кем-то час → ж о час о Fg для каждого час в Hom_C(FY, Икс). Hom (г, Gf) похож.

Определение через примыкание счетчика к единице

А примыкание округа к единице между двумя категориями C и D состоит из двух функторы F : D → C и г : C → D и два естественные преобразования

${\displaystyle {\begin{aligned}\varepsilon &:FG\to 1_{\mathcal {C}}\\\eta &:1_{\mathcal {D}}\to GF\end{aligned}}}$

соответственно назвал графство и единица измерения примыкания (терминология из универсальная алгебра ), так что композиции

${\displaystyle F{\xrightarrow {\;F\eta \;}}FGF{\xrightarrow {\;\varepsilon F\,}}F}$

${\displaystyle G{\xrightarrow {\;\eta G\;}}GFG{\xrightarrow {\;G\varepsilon \,}}G}$

тождественные преобразования 1_F и 1_г на F и г соответственно.

В этой ситуации мы говорим, что F слева примыкает к г и г прямо примыкает к F, и может указать эту связь, написав${\displaystyle (\varepsilon ,\eta ):F\dashv G}$ , или просто${\displaystyle F\dashv G}$ .

В форме уравнения вышеуказанные условия на (ε,η) являются count – unit уравнения

${\displaystyle {\begin{aligned}1_{F}&=\varepsilon F\circ F\eta \\1_{G}&=G\varepsilon \circ \eta G\end{aligned}}}$

что означает, что для каждого Икс в C и каждый Y в D,

${\displaystyle {\begin{aligned}1_{FY}&=\varepsilon _{FY}\circ F(\eta _{Y})\\1_{GX}&=G(\varepsilon _{X})\circ \eta _{GX}\end{aligned}}}$.

Обратите внимание, что ${\displaystyle 1_{\mathcal {C}}}$ обозначает идентифицирующий функтор на категории ${\displaystyle {\mathcal {C}}}$, ${\displaystyle 1_{F}}$ обозначает тождественное естественное преобразование от функтора F себе, и ${\displaystyle 1_{FY}}$ обозначает тождественный морфизм объекта FY.

Эти уравнения полезны для сведения доказательств сопряженных функторов к алгебраическим манипуляциям. Их иногда называют тождества треугольников, или иногда зигзагообразные уравнения из-за появления соответствующего строковые диаграммы. Чтобы запомнить их, сначала нужно написать бессмысленное уравнение ${\displaystyle 1=\varepsilon \circ \eta }$ а затем заполните либо F или г одним из двух простых способов, определяющих композиции.

Примечание. Использование префикса «co» в счетчике здесь не согласуется с терминологией пределов и копределов, поскольку копредел удовлетворяет начальный свойство, тогда как морфизмы коит будут удовлетворять Терминал свойства, и двойственно. Период, термин единица измерения здесь заимствовано из теории монады где это выглядит как вставка тождества 1 в моноид.

История

Идея сопряженных функторов была введена Даниэль Кан в 1958 г.^[2] Подобно многим концепциям теории категорий, он был предложен гомологическая алгебра, который в то время был посвящен вычислениям. Те, кто сталкивался с аккуратным, систематическим изложением предмета, заметили бы такие отношения, как

хом (F(Икс), Y) = hom (Икс, г(Y))

в категории абелевы группы, где F был функтором ${\displaystyle -\otimes A}$ (т.е. взять тензорное произведение с участием А), и г был функтором hom (А, -) (теперь это известно как тензор-гом присоединение ). Использование равно знак злоупотребление обозначениями; эти две группы не совсем идентичны, но есть способ их идентифицировать, естественный. Это можно считать естественным на основании, во-первых, того, что это два альтернативных описания билинейные отображения от Икс × А к Y. Это, однако, нечто особенное в случае тензорного произведения. В теории категорий «естественность» взаимно однозначности включается в понятие естественный изоморфизм.

Повсеместность

Если начать искать эти сопряженные пары функторов, они окажутся очень распространенными в абстрактная алгебра, а также в других местах. Пример ниже демонстрирует это; более того, универсальные конструкции, которые могут быть кому-то более знакомы, порождают множество сопряженных пар функторов.

В соответствии с мышлением Saunders Mac Lane, любая идея, например сопряженные функторы, которая достаточно широко встречается в математике, должна быть изучена сама по себе.^{[нужна цитата ]}

О концепциях можно судить по их использованию при решении проблем, а также по их использованию в построении теорий. Напряжение между этими двумя мотивами было особенно велико в 1950-х годах, когда теория категорий была первоначально разработана. Войти Александр Гротендик, который использовал теорию категорий для пеленгации компаса в другой работе - в функциональный анализ, гомологическая алгебра и наконец алгебраическая геометрия.

Вероятно, неверно утверждать, что он продвигал концепцию присоединенного функтора изолированно: но признание роли присоединения было неотъемлемой частью подхода Гротендика. Например, одним из его главных достижений была формулировка Двойственность Серра в относительной форме - грубо говоря, в непрерывном семействе алгебраических многообразий. Все доказательство основывалось на существовании правого сопряженного к некоторому функтору. Это нечто безусловно абстрактное и неконструктивное.^{[обсудить]}, но также по-своему мощно.

Примеры

Бесплатные группы

Конструкция бесплатные группы - распространенный и поучительный пример.

Позволять F : Набор → Grp быть функтором, присваивающим каждому набору Y то свободная группа порожденный элементами Y, и разреши г : Grp → Набор быть забывчивый функтор, который присваивает каждой группе Икс его базовый набор. потом F слева примыкает к г:

Начальные морфизмы. Для каждого набора Y, набор GFY это просто базовый набор свободной группы FY Сгенерированно с помощью Y. Позволять${\displaystyle \eta _{Y}:Y\to GFY}$ - отображение множества, заданное «включением образующих». Это первоначальный морфизм из Y к г, потому что любая заданная карта из Y к базовому набору ГВт какой-то группы W будет учитывать${\displaystyle \eta _{Y}:Y\to GFY}$ через единственный гомоморфизм групп из FY к W. Это в точности универсальное свойство свободной группы на Y.

Терминальные морфизмы. Для каждой группы Икс, группа FGX свободная группа, порожденная свободно GX, элементы Икс. Позволять${\displaystyle \varepsilon _{X}:FGX\to X}$ - групповой гомоморфизм, посылающий образующие FGX к элементам Икс они соответствуют, что существует в силу универсального свойства свободных групп. Тогда каждый${\displaystyle (GX,\varepsilon _{X})}$ является терминальным морфизмом из F к Икс, поскольку любой гомоморфизм группы из свободной группы FZ к Икс будет учитывать${\displaystyle \varepsilon _{X}:FGX\to X}$ через уникальную карту набора от Z к GX. Это значит, что (F,г) - присоединенная пара.

Примыкание хом-множества. Групповые гомоморфизмы из свободной группы FY группе Икс точно соответствуют картам из множества Y к набору GX: каждый гомоморфизм из FY к Икс полностью определяется своим действием на образующие, что является еще одним подтверждением универсального свойства свободных групп. Непосредственно можно проверить, что это соответствие является естественным преобразованием, что означает, что оно является присоединением гом-множества для пары (F,г).

примыкание округа к единице. Также можно непосредственно проверить естественность ε и η. Затем прямая проверка того, что они образуют примыкание единицы к единице${\displaystyle (\varepsilon ,\eta ):F\dashv G}$ составляет:

Первое уравнение единицы измерения  ${\displaystyle 1_{F}=\varepsilon F\circ F\eta }$ говорит, что для каждого набора Y сочинение

${\displaystyle FY{\xrightarrow {\;F(\eta _{Y})\;}}FGFY{\xrightarrow {\;\varepsilon _{FY}\,}}FY}$

должно быть тождество. Промежуточная группа FGFY свободная группа, свободно порожденная словами свободной группы FY. (Считайте, что эти слова заключены в скобки, чтобы указать, что они являются независимыми генераторами.) Стрелка${\displaystyle F(\eta _{Y})}$ - гомоморфизм групп из FY в FGFY отправка каждого генератора у из FY к соответствующему слову длины один (у) как генератор FGFY. Стрелка${\displaystyle \varepsilon _{FY}}$ - гомоморфизм групп из FGFY к FY отправляя каждый генератор на слово FY он соответствует (так что эта карта «опускает скобки»). Состав этих карт действительно тождественен на FY.

Второе уравнение единицы измерения  ${\displaystyle 1_{G}=G\varepsilon \circ \eta G}$ говорит, что для каждой группы Икс сочинение

 ${\displaystyle GX{\xrightarrow {\;\eta _{GX}\;}}GFGX{\xrightarrow {\;G(\varepsilon _{X})\,}}GX}$ 

должно быть тождество. Промежуточный набор GFGX это просто базовый набор FGX. Стрелка${\displaystyle \eta _{GX}}$ отображение множества "включение образующих" из множества GX к набору GFGX. Стрелка${\displaystyle G(\varepsilon _{X})}$ это установленная карта из GFGX к GX лежащий в основе гомоморфизма групп, отправляющий каждый генератор FGX к элементу Икс ему соответствует («отбрасывание скобок»). Состав этих карт действительно тождественен на GX.

Свободные конструкции и забывчивые функторы

Бесплатные объекты являются примерами левого сопряженного к забывчивый функтор который присваивает алгебраическому объекту его базовый набор. Эти алгебраические свободные функторы обычно имеют то же описание, что и в подробном описании ситуации со свободной группой выше.

Диагональные функторы и пределы

Продукты, волокнистые изделия, эквалайзеры, и ядра являются примерами категорического понятия предел. Любой предельный функтор сопряжен справа с соответствующим диагональным функтором (при условии, что категория имеет рассматриваемый тип пределов), а счетчик присоединения обеспечивает определяющие отображения из предельного объекта (т. Е. От диагонального функтора на пределе в категория функторов). Ниже приведены некоторые конкретные примеры.

• Продукты Пусть Π: Grp² → Grp функтор, который присваивает каждой паре (Икс₁, Икс₂) группа продуктов Икс₁×Икс₂, и пусть Δ: Grp → Grp² быть диагональный функтор который присваивает каждой группе Икс пара (Икс, Икс) в категории товаров Grp². Универсальность группы продуктов показывает, что сопряжена справа с Δ. Конечная точка этого присоединения является определяющей парой карт проекций из Икс₁×Икс₂ к Икс₁ и Икс₂ которые определяют предел, а единицей является диагональное включение группы X в Икс×Икс (отображение x в (x, x)).

В декартово произведение из наборы, произведение колец, произведение топологических пространств и т.д. по той же схеме; его также можно расширить более чем на два фактора. В более общем смысле любой тип предела сопряжен справа с диагональным функтором.

• Ядра. Рассмотрим категорию D гомоморфизмов абелевых групп. Если ж₁ : А₁ → B₁ и ж₂ : А₂ → B₂ два объекта D, то морфизм из ж₁ к ж₂ пара (г_А, г_B) морфизмов таких, что г_Bж₁ = ж₂г_А. Позволять г : D → Ab - функтор, сопоставляющий каждому гомоморфизму его ядро и разреши F : Ab → D - функтор, отображающий группу А к гомоморфизму А → 0. Тогда г прямо примыкает к F, что выражает универсальное свойство ядер. Конечным элементом этого присоединения является определяющее вложение ядра гомоморфизма в область гомоморфизма, а единицей является морфизм, идентифицирующий группу А с ядром гомоморфизма А → 0.

Подходящая вариация этого примера также показывает, что ядерные функторы для векторных пространств и модулей являются сопряженными справа. Аналогично можно показать, что коядровые функторы для абелевых групп, векторных пространств и модулей являются сопряженными слева.

Копределы и диагональные функторы

Сопутствующие товары, волокнистые побочные продукты, соэквалайзеры, и коядра являются примерами категорического понятия копредел. Любой функтор копредела сопряжен слева с соответствующим диагональным функтором (при условии, что категория имеет рассматриваемый тип копредела), а единица присоединения обеспечивает определяющие отображения в объект копредела. Ниже приведены некоторые конкретные примеры.

• Побочные продукты. Если F : Ab² → Ab присваивается каждой паре (Икс₁, Икс₂) абелевых групп их прямая сумма, и если г : Ab → Ab² - функтор, который сопоставляет каждой абелевой группе Y пара (Y, Y), тогда F слева примыкает к г, снова следствие универсальности прямых сумм. Единицей этой присоединенной пары является определяющая пара отображений включения из Икс₁ и Икс₂ в прямую сумму, а счетчик - это аддитивное отображение прямой суммы (Икс,Икс) вернуться к Икс (отправка элемента (а,б) прямой суммы к элементу а+б из Икс).

Аналогичные примеры дают прямая сумма из векторные пространства и модули, посредством бесплатный продукт групп и несвязным объединением множеств.

Дальнейшие примеры

Алгебра

• Присоединение идентичности к rng. Этот пример обсуждался в разделе мотивации выше. Учитывая rng р, мультипликативный элемент идентичности можно добавить, взяв рИксZ и определение Z-билинейное произведение с (r, 0) (0,1) = (0,1) (r, 0) = (r, 0), (r, 0) (s, 0) = (rs, 0), ( 0,1) (0,1) = (0,1). Это строит левый сопряженный к функтору, переводящий кольцо в базовый rng.
• Присоединение идентичности к полугруппа. Аналогично для полугруппы S, мы можем добавить элемент идентичности и получить моноид взяв несвязный союз S ${\displaystyle \sqcup }$ {1} и определив на нем бинарную операцию, чтобы она расширяла операцию на S а 1 - элемент идентичности. Эта конструкция дает функтор, сопряженный слева к функтору, переводящему моноид в нижележащую полугруппу.
• Расширения кольца. Предположим р и S кольца, а ρ: р → S это кольцевой гомоморфизм. потом S можно рассматривать как (слева) р-модуль, а тензорное произведение с участием S дает функтор F : р-Мод → S-Мод. потом F остается сопряженным с забывчивым функтором г : S-Мод → р-Мод.
• Тензорные продукты. Если р кольцо и M это право р-модуль, то тензорное произведение с M дает функтор F : р-Мод → Ab. Функтор г : Ab → р-Мод, определяется г(А) = hom_Z(M,А) для каждой абелевой группы А, является правым прилеганием к F.
• От моноидов и групп к кольцам. В цельное моноидное кольцо конструкция дает функтор из моноиды к кольцам. Этот функтор сопряжен слева с функтором, который ставит в соответствие данному кольцу лежащий в его основе мультипликативный моноид. Точно так же целое групповое кольцо конструкция дает функтор из группы кольцам, сопряженным слева к функтору, который ставит в соответствие данному кольцу его группа единиц. Также можно начать с поле K и рассмотрим категорию K-алгебры вместо категории колец, чтобы получить моноид и групповые кольца над K.
• Поле дробей. Рассмотрим категорию Дом_м областей целостности с инъективными морфизмами. Забывчивый функтор Поле → Дом_м from fields имеет левый сопряженный элемент - каждой области целостности присваивается ее поле дробей.
• Кольца полиномов. Позволять Кольцо_* - категория точечных коммутативных колец с единицей (пары (A, a), где A - кольцо, a ∈ A, а морфизмы сохраняют выделенные элементы). Забывчивый функтор G:Кольцо_* → Кольцо имеет левый сопряженный - каждому кольцу R сопоставляется пара (R [x], x), где R [x] - кольцо многочленов с коэффициентами из R.
• Абелианизация. Рассмотрим функтор включения г : Ab → Grp от категория абелевых групп к категория групп. Он имеет левое сопряжение, называемое абелианизация который присваивает каждой группе г фактор-группа г^ab=г/[г,г].
• Группа Гротендика. В K-теория, отправной точкой является наблюдение, что категория векторные пучки на топологическое пространство имеет структуру коммутативного моноида при прямая сумма. Можно сделать абелева группа из этого моноида Группа Гротендик, формально добавляя аддитивную инверсию для каждого пучка (или класса эквивалентности). В качестве альтернативы можно заметить, что функтор, который для каждой группы принимает основной моноид (игнорируя обратные), имеет левое сопряженное соединение. Это универсальная конструкция, соответствующая обсуждению в третьем разделе выше. То есть можно имитировать построение отрицательные числа; но есть и другой вариант теорема существования. В случае финитарных алгебраических структур само существование может быть отнесено к универсальная алгебра, или теория моделей; естественно, есть еще и доказательство, адаптированное к теории категорий.
• Взаимность Фробениуса в теория представлений групп: увидеть индуцированное представление. Этот пример примерно на полвека предвосхитил общую теорию.

Топология

• Функтор с левым и правым сопряженными. Позволять г быть функтором от топологические пространства к наборы который связывает с каждым топологическим пространством его базовое множество (то есть забывая о топологии). г имеет левый сопряженный F, создавая дискретное пространство на съемочной площадке Y, и правый сопряженный ЧАС создание тривиальная топология на Y.
• Подвесы и петлевые пространства. Данный топологические пространства Икс и Y, космос [SX, Y] из гомотопические классы карт из подвеска SX из Икс к Y естественно изоморфно пространству [Икс, ΩY] гомотопических классов отображений из Икс к пространство петли ΩY из Y. Таким образом, функтор надстройки сопряжен слева с функтором пространства петель в гомотопическая категория, важный факт в теория гомотопии.
• Камне-чехословацкая компактификация. Позволять KHaus быть категорией компактный Хаусдорфовы пространства и г : KHaus → верхний - функтор включения в категорию топологические пространства. потом г имеет левый сопряженный F : верхний → KHaus, то Каменно-чешская компактификация. Единица этой присоединенной пары дает непрерывный карта из каждого топологического пространства Икс в его каменно-чешскую компактификацию.
• Прямые и прообразы пучков. Каждые непрерывная карта ж : Икс → Y между топологические пространства индуцирует функтор ж _∗ из разряда снопы (множеств, или абелевых групп, или колец ...) на Икс соответствующей категории пучков на Y, то функтор прямого изображения. Он также индуцирует функтор ж ⁻¹ из категории пучков абелевых групп на Y в категорию пучков абелевых групп на Икс, то функтор обратного изображения. ж ⁻¹ слева примыкает к ж _∗. Здесь более тонкий момент заключается в том, что левый сопряженный для когерентные пучки будет отличаться от такового для пучков (наборов).
• Отрезвление. Статья о Каменная двойственность описывает связь между категорией топологических пространств и категорией трезвые пространства это известно как отрезвление. Примечательно, что статья также содержит подробное описание еще одного примыкания, которое подготавливает почву для знаменитого двойственность трезвых пространств и пространственных локаций, эксплуатируемых в бессмысленная топология.

Позы

Каждые частично заказанный набор можно рассматривать как категорию (где элементы poset становятся объектами категории, и у нас есть единственный морфизм из Икс к у если и только если Икс ≤ у). Пара сопряженных функторов между двумя частично упорядоченными множествами называется Связь Галуа (или, если это контравариантно, антитон Связь Галуа). См. Эту статью для ряда примеров: случай Теория Галуа конечно, ведущий. Любая связь Галуа порождает операторы закрытия и к обратному сохранению порядка биекций между соответствующими замкнутыми элементами.

Как и в случае с группами Галуа, реальный интерес часто заключается в уточнении соответствия двойственность (т.е. антитон порядковый изоморфизм). Рассмотрение теории Галуа в этом направлении Капланский оказал влияние на признание здесь общей структуры.

Случай частичного порядка довольно заметно сокращает определения присоединения, но может предоставить несколько тем:

• присоединения могут не быть дуальностями или изоморфизмами, но являются кандидатами на повышение до этого статуса
• операторы закрытия могут указывать на наличие присоединений, как соответствующие монады (ср. Аксиомы замыкания Куратовского )
• очень общий комментарий Уильям Ловер^[3] в том, что синтаксис и семантика соприкасаются: взять C быть набором всех логических теорий (аксиоматизаций), и D набор мощности набора всех математических структур. Для теории Т в C, позволять г(Т) - множество всех структур, удовлетворяющих аксиомам Т; для набора математических структур S, позволять F(S) - минимальная аксиоматизация S. Тогда мы можем сказать, что S это подмножество г(Т) если и только если F(S) логически следует Т: "семантический функтор" г справа примыкает к "синтаксическому функтору" F.
• деление это (в общем) попытка инвертировать умножение, но в ситуациях, когда это невозможно, мы часто пытаемся построить прилегающий вместо этого: идеальное частное сопряжено с умножением на идеалы кольца, а значение в логика высказываний примыкает к логическое соединение.

Теория категорий

• Эквивалентности. Если F : D → C является эквивалентность категорий, то имеем обратную эквивалентность г : C → D, а два функтора F и г образуют сопряженную пару. В этом случае единица и коединицы являются естественными изоморфизмами.
• Серия дополнений. Функтор π₀ который присваивает категории ее набор компонент связности, сопряженный слева функтору D который присваивает набору дискретную категорию на этом наборе. Более того, D сопряжена слева с функтором объекта U который присваивает каждой категории свой набор объектов, и, наконец, U слева сопряжена с А который присваивает каждому набору недискретную категорию^[4] на этом наборе.
• Экспоненциальный объект. В декартова закрытая категория эндофунктор C → C дается - ×А имеет право сопрягать -^А. Эту пару часто называют карри и не торопясь; во многих частных случаях они также непрерывны и образуют гомеоморфизм.

Категориальная логика

• Количественная оценка. Если ${\displaystyle \phi _{Y}}$ является унарным предикатом, выражающим некоторое свойство, то достаточно сильная теория множеств может доказать существование множества ${\displaystyle Y=\{y\mid \phi _{Y}(y)\}}$ условий, выполняющих свойство. Правильное подмножество ${\displaystyle T\subset Y}$ и связанная с этим инъекция ${\displaystyle T}$ в ${\displaystyle Y}$ характеризуется предикатом ${\displaystyle \phi _{T}(y)=\phi _{Y}(y)\land \varphi (y)}$ выражая строго более ограничительное свойство.

Роль кванторы в логике предикатов заключается в формировании предложений, а также в выражении сложных предикатов путем замыкания формул с возможно большим количеством переменных. Например, рассмотрим предикат ${\displaystyle \psi _{f}}$ с двумя открытыми переменными вида ${\displaystyle X}$ и ${\displaystyle Y}$. Использование квантификатора для закрытия ${\displaystyle X}$, мы можем сформировать множество

${\displaystyle \{y\in Y\mid \exists x.\,\psi _{f}(x,y)\land \phi _{S}(x)\}}$

всех элементов ${\displaystyle y}$ из ${\displaystyle Y}$ для которого есть ${\displaystyle x}$ к чему это ${\displaystyle \psi _{f}}$-связанный, и который сам характеризуется собственностью ${\displaystyle \phi _{S}}$. Теоретико-множественные операции, такие как пересечение ${\displaystyle \cap }$ двух наборов прямо соответствует соединению ${\displaystyle \land }$ предикатов. В категориальная логика, подполе теория топоса, кванторы отождествляются с сопряженными к функтору отката. Такую реализацию можно увидеть по аналогии с обсуждением логики высказываний с использованием теории множеств, но общее определение дает более широкий диапазон логик.

Итак, рассмотрим объект ${\displaystyle Y}$ в категории с откатами. Любой морфизм ${\displaystyle f:X\to Y}$ индуцирует функтор

${\displaystyle f^{*}:{\text{Sub}}(Y)\longrightarrow {\text{Sub}}(X)}$

на категории, являющейся предзаказом подобъектов. Отображает подобъекты ${\displaystyle T}$ из ${\displaystyle Y}$ (технически: классы мономорфизма ${\displaystyle T\to Y}$) к откату ${\displaystyle X\times _{Y}T}$. Если у этого функтора есть левый или правый сопряженный, они называются ${\displaystyle \exists _{f}}$ и ${\displaystyle \forall _{f}}$соответственно.^[5] Они оба отображают из ${\displaystyle {\text{Sub}}(X)}$ вернуться к ${\displaystyle {\text{Sub}}(Y)}$. Грубо говоря, учитывая домен ${\displaystyle S\subset X}$ для количественной оценки отношения, выраженного через ${\displaystyle f}$ над, функтор / квантор закрывается ${\displaystyle X}$ в ${\displaystyle X\times _{Y}T}$ и возвращает указанное таким образом подмножество ${\displaystyle Y}$.

пример: В ${\displaystyle \operatorname {Set} }$, категория множеств и функций, канонические подобъекты являются подмножеством (точнее их каноническими инъекциями). Откат ${\displaystyle f^{*}T=X\times _{Y}T}$ инъекции подмножества ${\displaystyle T}$ в ${\displaystyle Y}$ вместе ${\displaystyle f}$ характеризуется как самый большой набор, который знает все о ${\displaystyle f}$ и введение ${\displaystyle T}$ в ${\displaystyle Y}$. Таким образом, оказывается (взаимно однозначно) прообраз ${\displaystyle f^{-1}[T]\subseteq X}$.

Для ${\displaystyle S\subseteq X}$, выясним левый сопряженный, который определяется через

${\displaystyle {\operatorname {Hom} }(\exists _{f}S,T)\cong {\operatorname {Hom} }(S,f^{*}T),}$

что здесь просто означает

${\displaystyle \exists _{f}S\subseteq T\leftrightarrow S\subseteq f^{-1}[T]}$.

Рассматривать ${\displaystyle f[S]\subseteq T}$. Мы видим ${\displaystyle S\subseteq f^{-1}[f[S]]\subseteq f^{-1}[T]}$. Наоборот, если для ${\displaystyle x\in S}$ у нас также есть ${\displaystyle x\in f^{-1}[T]}$, то ясно ${\displaystyle f(x)\in T}$. Так ${\displaystyle S\subseteq f^{-1}[T]}$ подразумевает ${\displaystyle f[S]\subseteq T}$. Делаем вывод, что сопряженный слева к функтору прообраза ${\displaystyle f^{*}}$ дается прямым изображением. Вот характеристика этого результата, которая больше соответствует логической интерпретации: Изображение ${\displaystyle S}$ под ${\displaystyle \exists _{f}}$ это полный набор ${\displaystyle y}$такие, что ${\displaystyle f^{-1}[\{y\}]\cap S}$ не пусто. Это работает, потому что не учитываются именно те ${\displaystyle y\in Y}$ которые входят в состав ${\displaystyle f[S]}$. Так

${\displaystyle \exists _{f}S=\{y\in Y\mid \exists (x\in f^{-1}[\{y\}]).\,x\in S\;\}=f[S].}$

По аналогии с нашей мотивацией ${\displaystyle \{y\in Y\mid \exists x.\,\psi _{f}(x,y)\land \phi _{S}(x)\}}$.

Правый сопряженный к функтору обратного изображения задается (без выполнения вычислений здесь) как

${\displaystyle \forall _{f}S=\{y\in Y\mid \forall (x\in f^{-1}[\{y\}]).\,x\in S\;\}.}$

Подмножество ${\displaystyle \forall _{f}S}$ из ${\displaystyle Y}$ характеризуется как полный набор ${\displaystyle y}$со свойством, что прообраз ${\displaystyle \{y\}}$ относительно ${\displaystyle f}$ полностью содержится в ${\displaystyle S}$. Обратите внимание, что предикат, определяющий набор, такой же, как и выше, за исключением того, что ${\displaystyle \exists }$ заменяется на ${\displaystyle \forall }$.

Смотрите также powerset.

Дополнения полностью

Следовательно, существует множество функторов и естественных преобразований, связанных с каждым присоединением, и лишь небольшой части достаточно для определения остальных.

An примыкание между категориями C и D состоит из

• А функтор F : D → C называется левый смежный
• Функтор г : C → D называется правый смежный
• А естественный изоморфизм Φ: hom_C(F-, -) → hom_D(–,г–)
• А естественная трансформация ε: FG → 1_C называется графство
• Естественное преобразование η: 1_D → GF называется единица измерения

Эквивалентная формулировка, где Икс обозначает любой объект C и Y обозначает любой объект D, составляет:

Для каждого C-морфизм ж : FY → Икс, есть уникальный D-морфизм Φ_{Y, Икс}(ж) = г : Y → GX такие, что диаграммы ниже коммутируют, и для каждого D-морфизм г : Y → GX, есть уникальный C-морфизм Φ⁻¹_{Y, Икс}(г) = ж : FY → Икс в C такие, что диаграммы ниже коммутируют:

Из этого утверждения можно вывести, что:

• Преобразования ε, η и Φ связаны уравнениями

${\displaystyle {\begin{aligned}f=\Phi _{Y,X}^{-1}(g)&=\varepsilon _{X}\circ F(g)&\in &\,\,\mathrm {hom} _{C}(F(Y),X)\\g=\Phi _{Y,X}(f)&=G(f)\circ \eta _{Y}&\in &\,\,\mathrm {hom} _{D}(Y,G(X))\\\Phi _{GX,X}^{-1}(1_{GX})&=\varepsilon _{X}&\in &\,\,\mathrm {hom} _{C}(FG(X),X)\\\Phi _{Y,FY}(1_{FY})&=\eta _{Y}&\in &\,\,\mathrm {hom} _{D}(Y,GF(Y))\\\end{aligned}}}$

• Преобразования ε, η удовлетворяют уравнениям единичных единиц

${\displaystyle {\begin{aligned}1_{FY}&=\varepsilon _{FY}\circ F(\eta _{Y})\\1_{GX}&=G(\varepsilon _{X})\circ \eta _{GX}\end{aligned}}}$

• Каждая пара (GX, ε_Икс) это терминальный морфизм от F к Икс в C
• Каждая пара (FY, η_Y) является начальный морфизм от Y к г в D

В частности, приведенные выше уравнения позволяют определить Φ, ε и η в терминах любого из трех. Однако сопряженные функторы F и г одних обычно недостаточно для определения примыкания. Эквивалентность этих ситуаций демонстрируется ниже.

Универсальные морфизмы индуцируют присоединение гом-множеств

Для правого сопряженного функтора г : C → D; в смысле начальных морфизмов, можно построить индуцированное присоединение гом-множества, выполнив следующие шаги.

• Построить функтор F : D → C и естественное преобразование η.
  • Для каждого объекта Y в D, выберите начальный морфизм (F(Y), η_Y) от Y к г, так что η_Y : Y → г(F(Y)). У нас есть карта F на объектах и ​​семействе морфизмов η.
  • Для каждого ж : Y₀ → Y₁, так как (F(Y₀), η_Y0) является начальным морфизмом, то факторизуйте η_Y1 о ж с η_Y0 и получить F(ж) : F(Y₀) → F(Y₁). Это карта F на морфизмы.
  • Из коммутирующей диаграммы этой факторизации следует коммутирующая диаграмма естественных преобразований, так что η: 1_D → г о F это естественная трансформация.
  • Уникальность той факторизации и той г - функтор, следует, что отображение F на морфизмах сохраняет композиции и тождества.
• Построить естественный изоморфизм Φ: hom_C(F-, -) → hom_D(-,г-).
  • Для каждого объекта Икс в C, каждый объект Y в D, так как (F(Y), η_Y) - начальный морфизм, то Φ_{Y, Икс} биекция, где Φ_{Y, Икс}(ж : F(Y) → Икс) = г(ж) о η_Y.
  • η - естественное преобразование, г является функтором, то для любых объектов Икс₀, Икс₁ в C, любые предметы Y₀, Y₁ в D, Любые Икс : Икс₀ → Икс₁, Любые у : Y₁ → Y₀, имеем Φ_{Y1, Икс1}(Икс о ж о F(у)) = G (х) о г(ж) о г(F(у)) о η_Y1 = г(Икс) о г(ж) о η_Y0 о у = г(Икс) о Φ_{Y0, Икс0}(ж) о у, и тогда Φ естественно по обоим рассуждениям.

Аналогичное рассуждение позволяет построить присоединение гом-множества терминальных морфизмов к левому сопряженному функтору. (Конструкция, которая начинается с правого сопряженного, немного более распространена, поскольку правый сопряженный во многих сопряженных парах является тривиально определенным включением или забывчивым функтором.)

примыкание-единица индуцирует присоединение гом-множества

Данные функторы F : D → C, г : C → D, и присоединение коединицы к единице (ε, η): F ${\displaystyle \dashv }$ г, мы можем построить присоединение hom-множества, найдя естественное преобразование Φ: hom_C(F-, -) → hom_D(-,г-) в следующих шагах:

• Для каждого ж : FY → Икс и каждый г : Y → GX, определить

${\displaystyle {\begin{aligned}\Phi _{Y,X}(f)=G(f)\circ \eta _{Y}\\\Psi _{Y,X}(g)=\varepsilon _{X}\circ F(g)\end{aligned}}}$

Преобразования Φ и естественны, так как η и ε естественны.

• Используя, по порядку, что F - функтор, ε натуральное, а уравнение единицы 1_FY = ε_FY о F(η_Y), мы получаем

${\displaystyle {\begin{aligned}\Psi \Phi f&=\varepsilon _{X}\circ FG(f)\circ F(\eta _{Y})\\&=f\circ \varepsilon _{FY}\circ F(\eta _{Y})\\&=f\circ 1_{FY}=f\end{aligned}}}$

следовательно, ΨΦ - тождественное преобразование.

• Кроме того, используя это г - функтор, что η натуральное, и уравнение единицы единицы 1_GX = г(ε_Икс) о η_GX, мы получаем

${\displaystyle {\begin{aligned}\Phi \Psi g&=G(\varepsilon _{X})\circ GF(g)\circ \eta _{Y}\\&=G(\varepsilon _{X})\circ \eta _{GX}\circ g\\&=1_{GX}\circ g=g\end{aligned}}}$

следовательно, ΦΨ - тождественное преобразование. Таким образом, Φ - естественный изоморфизм с обратным Φ⁻¹ = Ψ.

Присоединение гом-множеств индуцирует все вышеперечисленное

Данные функторы F : D → C, г : C → D, и присоединение hom-множества Φ: hom_C(F-, -) → hom_D(-,г-), можно построить конъюнктивно-единичное присоединение

${\displaystyle (\varepsilon ,\eta ):F\dashv G}$ ,

который определяет семейства начальных и конечных морфизмов, на следующих этапах:

• Позволять${\displaystyle \varepsilon _{X}=\Phi _{GX,X}^{-1}(1_{GX})\in \mathrm {hom} _{C}(FGX,X)}$ для каждого Икс в C, где${\displaystyle 1_{GX}\in \mathrm {hom} _{D}(GX,GX)}$ - морфизм тождества.
• Позволять${\displaystyle \eta _{Y}=\Phi _{Y,FY}(1_{FY})\in \mathrm {hom} _{D}(Y,GFY)}$ для каждого Y в D, где${\displaystyle 1_{FY}\in \mathrm {hom} _{C}(FY,FY)}$ - морфизм тождества.
• Из биективности и естественности Φ следует, что каждое (GX, ε_Икс) - терминальный морфизм из F к Икс в C, и каждый (FY, η_Y) - начальный морфизм из Y к г в D.
• Естественность Φ влечет естественность ε и η, и две формулы

${\displaystyle {\begin{aligned}\Phi _{Y,X}(f)=G(f)\circ \eta _{Y}\\\Phi _{Y,X}^{-1}(g)=\varepsilon _{X}\circ F(g)\end{aligned}}}$

для каждого ж: FY → Икс и г: Y → GX (которые полностью определяют Φ).

• Подстановка FY для Икс и η_Y = Φ_{Y, FY}(1_FY) для г во второй формуле дает первое уравнение единицы измерения

${\displaystyle 1_{FY}=\varepsilon _{FY}\circ F(\eta _{Y})}$,

и заменяя GX для Y и ε_Икс = Φ⁻¹_{GX, X}(1_GX) для ж в первой формуле дает второе уравнение единицы измерения

${\displaystyle 1_{GX}=G(\varepsilon _{X})\circ \eta _{GX}}$.

Свойства

Существование

Смотрите также: Формальные критерии для присоединенных функторов

Не каждый функтор г : C → D допускает левый сопряженный. Если C это полная категория, то функторы с сопряженными слева можно охарактеризовать теорема о сопряженном функторе из Питер Дж. Фрейд: г имеет левый сопряженный тогда и только тогда, когда он непрерывный и выполняется определенное условие малости: для каждого объекта Y из D существует семейство морфизмов

ж_я : Y → г(Икс_я)

где индексы я пришли из набор я, а не правильный класс, так что каждый морфизм

час : Y → г(Икс)

можно записать как

час = г(т) o ж_я

для некоторых я в я и немного морфизма

т : Икс_я → Икс в C.

Аналогичное утверждение характеризует функторы с правым сопряженным элементом.

Важным частным случаем является случай местные презентабельные категории. Если ${\displaystyle F:C\to D}$ является функтором между локально представимыми категориями, то

• F имеет правый сопряженный тогда и только тогда, когда F сохраняет маленькие копределы
• F имеет левый сопряженный тогда и только тогда, когда F сохраняет небольшие пределы и является доступный функтор

Уникальность

Если функтор F : D → C имеет два правых сопряжения г и г', тогда г и г' находятся естественно изоморфный. То же верно и для левых сопряженных.

Наоборот, если F слева примыкает к г, и г естественно изоморфен г' тогда F также примыкает к г′. В более общем смысле, если 〈F, г, ε, η〉 является присоединением (с единицей единицы (ε, η)) и

σ: F → F′

τ: г → г′

являются естественными изоморфизмами, то 〈F′, г′, Ε ′, η ′〉 - присоединение, где

${\displaystyle {\begin{aligned}\eta '&=(\tau \ast \sigma )\circ \eta \\\varepsilon '&=\varepsilon \circ (\sigma ^{-1}\ast \tau ^{-1}).\end{aligned}}}$

Вот ${\displaystyle \circ }$ обозначает вертикальную композицию естественных преобразований, а ${\displaystyle \ast }$ обозначает горизонтальную композицию.

Сочинение

Дополнения могут быть составлены естественным образом. В частности, если 〈F, г, ε, η〉 - присоединение между C и D и <F′, г′, Ε ′, η ′〉 - присоединение между D и E тогда функтор

${\displaystyle F\circ F':E\rightarrow C}$

слева примыкает к

${\displaystyle G'\circ G:C\to E.}$

Точнее, между F F ' и G 'G с единицей и счетом, заданными соответственно составами:

${\displaystyle {\begin{aligned}&1_{\mathcal {E}}{\xrightarrow {\eta '}}G'F'{\xrightarrow {G'\eta F'}}G'GFF'\\&FF'G'G{\xrightarrow {F\varepsilon 'G}}FG{\xrightarrow {\varepsilon }}1_{\mathcal {C}}.\end{aligned}}}$

Это новое присоединение называется сочинение из двух данных добавок.

Поскольку существует также естественный способ определить тождественное соединение между категорией C и сам, тогда можно сформировать категорию, объекты которой все малые категории и чьи морфизмы являются присоединениями.

Ограничить сохранение

Самым важным свойством сопряженных является их непрерывность: каждый функтор, имеющий сопряженный слева (и, следовательно, является правый сопряженный) является непрерывный (т.е. ездит с пределы в теоретико-категориальном смысле); каждый функтор, имеющий правый сопряженный (и, следовательно, является левый сопряженный) является непрерывный (т.е. ездит с копределы ).

Поскольку многие общие конструкции в математике являются пределами или копределами, это дает большой объем информации. Например:

• применяя правый сопряженный функтор к товар объектов дает продукт изображений;
• применяя левый сопряженный функтор к сопродукт объектов дает копродукт изображений;
• каждый правый сопряженный функтор между двумя абелевыми категориями есть осталось точно;
• каждый левый сопряженный функтор между двумя абелевыми категориями есть прямо точно.

Аддитивность

Если C и D находятся предаддитивные категории и F : D → C является аддитивный функтор с правым примыканием г : C → D, тогда г также является аддитивным функтором, а биекции hom-множества

${\displaystyle \Phi _{Y,X}:\mathrm {hom} _{\mathcal {C}}(FY,X)\cong \mathrm {hom} _{\mathcal {D}}(Y,GX)}$

на самом деле являются изоморфизмами абелевых групп. Вдвойне, если г аддитивен с левым сопряженным F, тогда F также является аддитивным.

Более того, если оба C и D находятся аддитивные категории (т.е. предаддитивные категории со всеми конечными побочные продукты ), то любая пара сопряженных между ними функторов автоматически аддитивна.

Отношения

Универсальные конструкции

Как указывалось ранее, связь между категориями C и D рождает семью универсальные морфизмы, по одному на каждый объект в C и по одному на каждый объект в D. Наоборот, если существует универсальный морфизм функтора г : C → D от каждого объекта D, тогда г имеет левый сопряженный.

Однако универсальные конструкции более общие, чем присоединенные функторы: универсальная конструкция подобна задаче оптимизации; она порождает присоединенную пару тогда и только тогда, когда эта проблема имеет решение для каждого объекта D (эквивалентно, каждый объект C).

Эквивалентность категорий

Если функтор F : D → C это половина эквивалентность категорий тогда это левый сопряженный в присоединенной эквивалентности категорий, т. е. присоединение, единица и коит которого являются изоморфизмами.

Каждое присоединение 〈F, г, ε, η〉 расширяет эквивалентность некоторых подкатегорий. Определить C₁ как полная подкатегория C состоящий из этих объектов Икс из C для которого ε_Икс является изоморфизмом, и определим D₁ как полная подкатегория из D состоящий из этих объектов Y из D для которого η_Y является изоморфизмом. потом F и г может быть ограничено D₁ и C₁ и дают обратные эквивалентности этих подкатегорий.

Таким образом, в некотором смысле сопряженные являются «обобщенно обратными». Однако обратите внимание, что правая инверсия F (т.е. функтор г такой, что FG естественно изоморфно 1_D) не обязательно должен быть правым (или левым) сопряженным с F. Смежные обобщают двусторонний обратное.

Монады

Каждое присоединение 〈F, г, ε, η〉 порождает ассоциированный монада 〈Т, η, μ〉 в категории D. Функтор

${\displaystyle T:{\mathcal {D}}\to {\mathcal {D}}}$

дан кем-то Т = GF. Единица монады

${\displaystyle \eta :1_{\mathcal {D}}\to T}$

есть просто единица η присоединения и преобразования умножения

${\displaystyle \mu :T^{2}\to T\,}$

дается формулой μ = гεF. Двойственно тройка 〈FG, ε, Fηг〉 Определяет комонада в C.

Каждая монада возникает из некоторого присоединения - фактически, как правило, из многих добавлений - описанным выше способом. Две конструкции, называемые категорией Алгебры Эйленберга – Мура и Категория Клейсли - два экстремальных решения проблемы построения присоединения, порождающего данную монаду.

Заметки

1. Баэз, Джон С. (1996). "Многомерная алгебра II: 2-гильбертовы пространства". arXiv:q-alg / 9609018.
2. Кан, Дэниел М. (1958). «Присоединенные функторы» (PDF). Труды Американского математического общества. 87 (2): 294–329. Дои:10.2307/1993102.
3. Лавер, Ф. Уильям, "Примыкание к основам ", Диалектика, 1969. Теперь обозначения другие; более легкое введение Питера Смита в этих конспектах лекций, которые также приписывают эту концепцию цитируемой статье.
4. «Недискретная категория». nLab.
5. Мак-Лейн, Сондерс; Мурдейк, Ике (1992) Пучки в геометрии и логике, Springer-Verlag. ISBN  0-387-97710-4 Страницу 58

использованная литература

• Адамек, Иржи; Херрлих, Хорст; Стрекер, Джордж Э. (1990). Абстрактные и конкретные категории. Радость кошек (PDF). Джон Вили и сыновья. ISBN  0-471-60922-6. Zbl  0695.18001.
• Мак-Лейн, Сондерс (1998). Категории для рабочего математика. Тексты для выпускников по математике. 5 (2-е изд.). Springer-Verlag. ISBN  0-387-98403-8. Zbl  0906.18001.

внешние ссылки

• Дополнения Семь коротких лекций по адъюнкциям Евгения Ченг Катстеров.
• WildCats пакет теории категорий для Mathematica. Манипуляция и визуализация объектов, морфизмы, категории, функторы, естественные преобразования, универсальные свойства.