Бесплатная категория - Free category

В математика, то свободная категория или же категория пути созданный ориентированный граф или же колчан это категория который является результатом свободного объединения стрелок, когда цель одной стрелки является источником следующей.

Точнее, объекты категории - это вершины колчана, а морфизмы - это пути между объектами. Здесь дорожка определяется как конечная последовательность

${\displaystyle V_{0}{\xrightarrow {\;\;E_{0}\;\;}}V_{1}{\xrightarrow {\;\;E_{1}\;\;}}\cdots {\xrightarrow {E_{n-1}}}V_{n}}$

куда ${\displaystyle V_{k}}$ вершина колчана, ${\displaystyle E_{k}}$ край колчана, и п колеблется в пределах неотрицательных целых чисел. Для каждой вершины ${\displaystyle V}$ колчана есть «пустой путь», который составляет тождественные морфизмы категории.

Операция композиции - это конкатенация путей. Данные пути

${\displaystyle V_{0}{\xrightarrow {E_{0}}}\cdots {\xrightarrow {E_{n-1}}}V_{n},\quad V_{n}{\xrightarrow {F_{0}}}W_{0}{\xrightarrow {F_{1}}}\cdots {\xrightarrow {F_{n-1}}}W_{m},}$

их состав

${\displaystyle \left(V_{n}{\xrightarrow {F_{0}}}W_{0}{\xrightarrow {F_{1}}}\cdots {\xrightarrow {F_{n-1}}}W_{m}\right)\circ \left(V_{0}{\xrightarrow {E_{0}}}\cdots {\xrightarrow {E_{n-1}}}V_{n}\right):=V_{0}{\xrightarrow {E_{0}}}\cdots {\xrightarrow {E_{n-1}}}V_{n}{\xrightarrow {F_{0}}}W_{0}{\xrightarrow {F_{1}}}\cdots {\xrightarrow {F_{n-1}}}W_{m}}$.^[1][2]

Обратите внимание, что результат композиции начинается с правого операнда композиции и заканчивается ее левым операндом.

Примеры

• Если Q колчан с одной вершиной и одним ребром ж от этого объекта к себе, затем свободная категория на Q имеет как стрелки 1, ж, ж∘ж,ж∘ж∘ж, так далее.^[2]
• Позволять Q быть колчаном с двумя вершинами а, б и два края е, ж из а к б и б к а, соответственно. Тогда свободная категория на Q имеет две тождественные стрелки и стрелку для каждой конечной последовательности чередующихся епесок жs, в том числе: е, ж, е∘ж, ж∘е, ж∘е∘ж, е∘ж∘е, так далее.^[1]
• Если Q это колчан ${\displaystyle a{\xrightarrow {f}}b{\xrightarrow {g}}c}$, то свободная категория на Q имеет (помимо трех тождественных стрелок) стрелки ж, грамм, и грамм∘ж.
• Если колчан Q имеет только одну вершину, то свободная категория на Q имеет только один объект и соответствует свободный моноид по краям Q.^[1]

Характеристики

В категория малых категорий Кот имеет забывчивый функтор U в категорию колчанов Quiv:

U : Кот → Quiv

который переводит объекты в вершины и морфизмы в стрелки. Интуитивно U «[забывает], какие стрелки являются составными, а какие идентичными».^[2] Этот забывчивый функтор правый смежный функтору, отправляющему колчан в соответствующую свободную категорию.

Универсальная собственность

Свободную категорию по колчану можно описать вплоть до изоморфизм по универсальная собственность. Позволять C : Quiv → Кот - функтор, переводящий колчан в свободную категорию на этом колчане (как описано выше), пусть U - забывчивый функтор, определенный выше, и пусть грамм быть любым колчаном. Тогда есть гомоморфизм графов я : грамм → U(C(грамм)) и с учетом любой категории D и любой гомоморфизм графов F : грамм → U (D), существует уникальный функтор F ' : C(грамм) → D такой, что U(F ')∘я=F, т.е. следующая диаграмма ездит на работу:

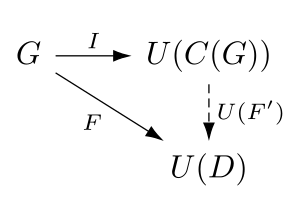
Функтор C является левый смежный забывчивому функтору U.^[1][2][3]

Смотрите также

• Математический портал

• Бесплатная строгая моноидальная категория
• Бесплатный объект
• Присоединенные функторы

Рекомендации

1. Awodey, Стив (2010). Теория категорий (2-е изд.). Оксфорд: Издательство Оксфордского университета. С. 20–24. ISBN  978-0199237180. OCLC  740446073.
2. Мак-Лейн, Сондерс (1978). Категории для рабочего математика (Второе изд.). Нью-Йорк, Нью-Йорк: Springer New York. С. 49–51. ISBN  1441931236. OCLC  851741862.
3. "бесплатная категория в nLab". ncatlab.org. Получено 2017-09-12.