Частично заказанный набор - Partially ordered set

В Диаграмма Хассе из набор всех подмножеств трехэлементного множества {x, y, z}, упорядоченного по включению. Разные наборы на одном горизонтальном уровне несопоставимы друг с другом. Некоторые другие пары, такие как {x} и {y, z}, также несравнимы.

В математика, особенно теория порядка, а частично заказанный набор (также посеть) формализует и обобщает интуитивную концепцию упорядочения, последовательности или расположения элементов набор. Посет состоит из набора вместе с бинарное отношение указывая, что для определенных пар элементов в наборе один из элементов предшествует другому в порядке. Само отношение называется «частичным порядком». Слово частичный в названиях «частичный порядок» и «частично упорядоченный набор» используется как указание на то, что не каждая пара элементов должна быть сопоставимой. То есть могут быть пары элементов, для которых ни один элемент не предшествует другому в poset. Таким образом, частичные заказы обобщают общее количество заказов, в котором каждая пара сопоставима.

Формально частичный порядок - это любое бинарное отношение, которое рефлексивный (каждый элемент сопоставим сам с собой), антисимметричный (никакие два разных элемента не предшествуют друг другу), и переходный (начало цепочки отношений приоритета должно предшествовать концу цепочки).

Один знакомый пример частично упорядоченного набора - это набор людей, упорядоченных по генеалогический потомство. Некоторые пары людей связаны отношениями потомков и предков, но другие пары людей несравнимы, и ни одна из них не является потомком другой.

Позет можно визуализировать через его Диаграмма Хассе, который отображает отношение порядка.[1]

Формальное определение

А (нестрогий) частичный заказ[2] это однородное бинарное отношение ≤ над набор п удовлетворяющие конкретным аксиомам, которые обсуждаются ниже. Когда а ≤ бмы говорим, что а является относится к б. (Это не означает, что б также связано с а, потому что отношение не обязательно симметричный.)

Аксиомы для нестрогого частичного порядка утверждают, что отношение ≤ равно рефлексивный, антисимметричный, и переходный. То есть для всех а, б, и c в п, он должен удовлетворять:

  1. а ≤ а (рефлексивность: каждый элемент связан с самим собой).
  2. если а ≤ б и б ≤ а, тогда а = б (антисимметрия: два разных элемента не могут быть связаны в обоих направлениях).
  3. если а ≤ б и б ≤ c, тогда а ≤ c (транзитивность: если первый элемент связан со вторым элементом, и, в свою очередь, этот элемент связан с третьим элементом, то первый элемент связан с третьим элементом).

Другими словами, частичный порядок - это антисимметричный Предварительный заказ.

Набор с частичным порядком называется частично заказанный набор (также называемый посеть). Период, термин заказанный набор иногда также используется, если из контекста ясно, что никакой другой порядок не подразумевается. Особенно, полностью упорядоченные наборы также могут называться «упорядоченные множества», особенно в областях, где эти структуры более распространены, чем посеты.

За а, б, элементы частично упорядоченного множества п, если а ≤ б или же б ≤ а, тогда а и б находятся сопоставимый. В противном случае они несравненный. На рисунке вверху справа, например, {x} и {x, y, z} сопоставимы, а {x} и {y} - нет. Частичный порядок, при котором каждая пара элементов сопоставима, называется общий заказ или же линейный порядок; полностью упорядоченный набор также называется цепь (например, натуральные числа в стандартном порядке). Подмножество чугуна, в котором никакие два различных элемента не сопоставимы, называется антицепь (например, набор синглтоны {{x}, {y}, {z}} на верхнем правом рисунке). Элемент а как говорят строго меньше чем элемент b, если а ≤ б и а≠б. Элемент а как говорят покрытый другим элементом б, написано а⋖б (или же а<:б), если а строго меньше, чем б и нет третьего элемента c умещается между ними; формально: если оба а≤б и а≠б верны, и а≤c≤б ложно для каждого c с а≠c≠б. Будет дано более краткое определение ниже в строгом порядке, соответствующем «≤». Например, {x} покрывается {x, z} на верхнем правом рисунке, но не {x, y, z}.

Примеры

Стандартные примеры позет, возникающих в математике, включают:

Extrema

Неотрицательные целые числа, упорядоченные по делимости
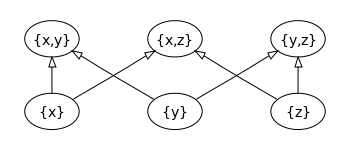На рисунке выше удалены наибольший и наименьший элементы. В этом уменьшенном poset верхний ряд элементов все максимальный элементы, а нижняя строка - все минимальный элементы, но нет величайший и нет наименее элемент. Множество {x, y} является верхняя граница для коллекции элементов {{x}, {y}}.

Есть несколько понятий "наибольший" и "наименьший" элемент в посете. п, а именно:

  • Величайший элемент и наименьший элемент: элемент грамм в п является наибольшим элементом, если для каждого элемента а в п, а ≤ грамм. Элемент м в п является наименьшим элементом, если для каждого элемента а в п, а ≥ м. У посета может быть только один наибольший или наименьший элемент.
  • Максимальные элементы и минимальные элементы: элемент грамм в P является максимальным элементом, если нет элемента а в п такой, что а > грамм. Аналогично элемент м в п является минимальным элементом, если нет элемента а в P такое, что а < м. Если ЧУМ имеет наибольший элемент, он должен быть единственным максимальным элементом, но в противном случае может быть более одного максимального элемента, и то же самое для наименьших элементов и минимальных элементов.
  • Верхняя и нижняя границы: Для подмножества А из п, элемент Икс в п является верхней границей А если а ≤ Икс, для каждого элемента а в А. Особенно, Икс не обязательно быть в А быть верхней границей А. Аналогично элемент Икс в п является нижней границей А если а ≥ Икс, для каждого элемента а в А. Величайший элемент п является верхней границей п сам, а наименьший элемент является нижней границей п.

Например, рассмотрим положительные целые числа, упорядоченный по делимости: 1 - наименьший элемент, так как он делит все остальные элементы; с другой стороны, этот poset не имеет наибольшего элемента (хотя, если бы один включил 0 в poset, который является кратным любому целому числу, это будет наибольшим элементом; см. рисунок). В этом частично упорядоченном множестве нет даже максимальных элементов, поскольку любые грамм делит, например, 2грамм, который отличается от него, поэтому грамм не является максимальным. Если число 1 исключено, сохраняя при этом делимость упорядочением по элементам больше 1, то результирующий элемент poset не будет иметь наименьшего элемента, но любой простое число минимальный элемент для него. В этом наборе 60 - это верхняя граница (но не наименьшая верхняя граница) подмножества {2, 3, 5, 10}, которое не имеет никакой нижней границы (поскольку 1 не входит в набор); с другой стороны, 2 - это нижняя граница подмножества степеней двойки, которая не имеет никакой верхней границы.

Заказы на декартово произведение частично упорядоченных множеств

Рефлексивное замыкание строгого прямого товарного заказа на ℕ × ℕ. Элементы покрытый по (3,3) и покрытие (3,3) выделены зеленым и красным цветом соответственно.
Заказ продукции на ℕ × ℕ
Лексикографический порядок на ℕ × ℕ

В порядке увеличения силы, то есть уменьшения наборов пар, три возможных частичных порядка на Декартово произведение из двух частично упорядоченных наборов (см. рисунки):

Все три аналогично можно определить для декартова произведения более двух наборов.

Применительно к упорядоченные векторные пространства над тем же поле, результатом в каждом случае также является упорядоченное векторное пространство.

Смотрите также заказы на декартово произведение полностью упорядоченных множеств.

Суммы частично упорядоченных наборов

Диаграмма Хассе из последовательно-параллельный частичный порядок, образованный как порядковая сумма трех меньших частичных порядков.

Еще один способ комбинировать два позы - это порядковая сумма[4] (или же линейная сумма[5]), Z = Икс ⊕ Y, определенный на объединении базовых множеств Икс и Y по заказу а ≤Z б если и только если:

  • а, б ∈ Икс с а ≤Икс б, или же
  • а, б ∈ Y с а ≤Y б, или же
  • а ∈ Икс и б ∈ Y.

Если два посета хорошо организованный, то и их порядковая сумма.[6]Операция порядкового суммирования - одна из двух операций, используемых для формирования последовательно-параллельные частичные порядки, и в этом контексте называется составлением серий. Другая операция, используемая для формирования этих порядков, несвязное объединение двух частично упорядоченных наборов (без отношения порядка между элементами одного набора и элементами другого набора) называется в этом контексте параллельной композицией.

Строгие и нестрогие частичные заказы

В некоторых случаях частичный порядок, определенный выше, называется нестрогий (или же рефлексивный) частичный заказ. В этих контекстах строгий (или же иррефлексивный) частичный заказ «<» - это бинарное отношение, иррефлексивный, переходный и асимметричный, т. е. удовлетворяет для всех а, б, и c в п:

  • нет а <а (нерефлексивность),
  • если а <б и б <с тогда а <с (транзитивность) и
  • если а <б тогда не б <а (асимметрия; подразумевает иррефлексивность; и подразумевается иррефлексивностью и антисимметрией[7]).

Строгие и нестрогие частичные заказы тесно связаны. Нестрогий частичный порядок можно преобразовать в строгий частичный порядок, удалив все отношения в форме а ≤ а. И наоборот, строгий частичный порядок может быть преобразован в нестрогий частичный порядок путем присоединения всех отношений этой формы. Таким образом, если «≤» является нестрогим частичным порядком, то соответствующий строгий частичный порядок «<» является иррефлексивное ядро предоставлено:

а < б если а ≤ б и а ≠ б

И наоборот, если «<» является строгим частичным порядком, то соответствующий нестрогий частичный порядок «≤» является рефлексивное закрытие предоставлено:

а ≤ б если а < б или же а = б.

Это причина использования обозначения «≤».

Используя строгий порядок "<", отношение "а покрывается б"можно эквивалентно перефразировать как"а<б, но нет а<c<б для любого c". Строгие частичные заказы полезны, поскольку они более точно соответствуют ориентированные ациклические графы (dags): каждый строгий частичный порядок является dag, а переходное закрытие дага - это как строгий частичный порядок, так и сам даг.

Обратный и двойной порядок

Обратное (или обратное) отношение частичного порядка ≤ - это разговаривать из ≤. Обычно обозначается ≥, это отношение, удовлетворяющее Икс ≥ у если и только если у ≤ Икс. Обратное отношение частичного порядка является рефлексивным, транзитивным и антисимметричным и, следовательно, само является отношением частичного порядка. В заказ двойной частично упорядоченного множества - это тот же набор, но отношение частичного порядка заменено на обратное. Иррефлексивное отношение> к ≥, как <к ≤.

Любое из четырех отношений ≤, <, ≥ и> на данном множестве однозначно определяет остальные три.

В общем два элемента Икс и у частичного порядка могут находиться в любом из четырех взаимоисключающих отношений друг с другом: либо Икс < у, или же Икс = у, или же Икс > у, или же Икс и у находятся несравненный (ни один из трех других). А полностью заказанный set - это тот, который исключает эту четвертую возможность: все пары элементов сопоставимы, и тогда мы говорим, что трихотомия держит. В натуральные числа, то целые числа, то рациональные, а реалы все полностью упорядочены по своей алгебраической (знаковой) величине, тогда как сложные числа не. Это не означает, что комплексные числа нельзя упорядочить полностью; мы могли бы, например, упорядочить их лексикографически через Икс+яу < ты+яv если и только если Икс < ты или же (Икс = ты и у < v), но это не порядок по величине в каком-либо разумном смысле, поскольку он делает 1 больше 100я. Упорядочивание их по абсолютной величине дает предварительный порядок, в котором все пары сопоставимы, но это не частичный порядок, поскольку 1 и я имеют одинаковую абсолютную величину, но не равны, что нарушает антисимметрию.

Отображения между частично упорядоченными наборами

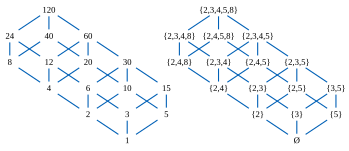Порядковый изоморфизм между делителями 120 (частично упорядочен по делимости) и замкнутыми по делителям подмножествами {2,3,4,5,8} (частично упорядочен по включению множества)
Сохраняющие порядок, но не отражающие порядок (поскольку ж(ты)≤ж(v), но нет ты≤v) карта.

Учитывая два частично упорядоченных набора (S, ≤) и (Т, ≤), функция ж: S → Т называется сохраняющий порядок, или же монотонный, или же изотон, если для всех Икс и у в S, Икс≤у подразумевает ж(Икс) ≤ ж(у).Если (U, ≤) также является частично упорядоченным множеством, и оба ж: S → Т и грамм: Т → U сохраняют порядок, их сочинение (грамм∘ж): S → U тоже сохраняет порядок. ж: S → Т называется отражающий порядок если для всех Икс и у в S, ж(Икс) ≤ ж(у) подразумевает Икс≤у.Если ж одновременно сохраняет и отражает порядок, то это называется встраивание порядка из (S, ≤) в (Т, ≤), в последнем случае ж обязательно инъективный, поскольку ж(Икс) = ж(у) подразумевает Икс ≤ у и у ≤ Икс. Если вложение порядка между двумя посетами S и Т существует, говорят, что S возможно встроенный в Т. Если заказ-встраивание ж: S → Т является биективный, это называется изоморфизм порядка, а частичные заказы (S, ≤) и (Т, ≤) называются изоморфный. Изоморфные порядки имеют сходные по структуре Диаграммы Хассе (см. рисунок справа). Можно показать, что если сохраняющие порядок карты ж: S → Т и грамм: Т → S существуют такие, что грамм∘ж и ж∘грамм дает функция идентичности на S и Тсоответственно, то S и Т изоморфны по порядку.[8]

Например, отображение ж: ℕ → ℙ (ℕ) из множества натуральных чисел (упорядоченных по делимости) к набор мощности натуральных чисел (упорядоченных включением множества) можно определить, взяв каждое число в набор его простые делители. Сохраняет порядок: если Икс разделяет у, то каждый простой делитель числа Икс также является простым делителем у. Однако он не является ни инъективным (поскольку он отображает как 12, так и 6 в {2,3}), ни отражением порядка (поскольку 12 не делит 6). Взяв вместо этого каждое число в набор его основная сила divisors определяет карту грамм: ℕ → ℙ (ℕ), который сохраняет порядок, отражает порядок и, следовательно, является вложением порядка. Это не изоморфизм порядка (поскольку он, например, не отображает какое-либо число в набор {4}), но его можно сделать по одному ограничение его кодомена к грамм(ℕ). На правом рисунке показано подмножество и его изоморфный образ при грамм. Построение такого изоморфизма порядка в набор степеней можно обобщить на широкий класс частичных порядков, называемых распределительные решетки, видеть "Теорема Биркгофа о представлении ".

Количество частичных заказов

Последовательность A001035 в OEIS дает количество частичных заказов на множестве п маркированные элементы:

Количество п-элементные бинарные отношения разных типов
ЭлементыЛюбойПереходныйРефлексивныйПредварительный заказЧастичный заказВсего предзаказОбщий заказОтношение эквивалентности
011111111
122111111
21613443322
35121716429191365
465,5363,9944,096355219752415
п2п22п2−п∑п
k=0  k! S (п, k)		п!∑п
k=0  S (п, k)
OEISA002416A006905A053763A000798A001035A000670A000142A000110

Количество строгих частичных заказов такое же, как и количество частичных заказов.

Если подсчет производится только вплоть до изоморфизм, последовательность 1, 1, 2, 5, 16, 63, 318,… (последовательность A000112 в OEIS ) получается.

Линейное расширение

Частичный порядок ≤* на съемочной площадке Икс является расширение другого частичного порядка ≤ на Икс при условии, что для всех элементов Икс и у из Икс, в любое время Икс ≤ у, также верно, что Икс ≤* у. А линейное расширение является расширением, которое также является линейным (то есть полным) порядком. Каждый частичный заказ может быть расширен до полного заказа (принцип расширения заказов ).[9]

В Информатика, алгоритмы нахождения линейных расширений частичных порядков (представленных как достижимость заказы ориентированные ациклические графы ) называются топологическая сортировка.

В теории категорий

Каждый посет (и каждый предварительно заказанный набор ) можно рассматривать как категория где, для объектов Икс и у, есть не более одного морфизм из Икс к у. Более явно, пусть hom (Икс, у) = {(Икс, у)} если Икс ≤ у (а в противном случае - пустое множество) и (у, z)∘(Икс, у) = (Икс, z). Такие категории иногда называют позетальный.

Позеты эквивалент друг другу тогда и только тогда, когда они изоморфный. В посете наименьший элемент, если он существует, является исходный объект, а самый большой элемент, если он существует, является конечный объект. Кроме того, каждый предварительно упорядоченный набор эквивалентен poset. Наконец, каждая подкатегория чугуна изоморфизм-замкнутый.

Частичные порядки в топологических пространствах

Основная статья: Частично упорядоченное пространство

Если п является частично упорядоченным множеством, которому также была придана структура топологическое пространство, то принято считать, что это закрыто подмножество топологических пространство продукта . В этом предположении отношения частичного порядка хорошо работают при пределы в том смысле, что если , и , и для всех   , тогда .[10]

Интервалы

An интервал в позе п это подмножество я из п с тем свойством, что для любого Икс и у в я и любой z в п, если Икс ≤ z ≤ у, тогда z также в я. (Это определение обобщает интервал определение действительных чисел.)

За а ≤ б, то закрытый интервал [а, б] это набор элементов Икс удовлетворение а ≤ Икс ≤ б (т.е. а ≤ Икс и Икс ≤ б). Он содержит как минимум элементы а и б.

Используя соответствующее строгое отношение "<", открытый интервал (а, б) это набор элементов Икс удовлетворение а < Икс < б (т.е. а < Икс и Икс < б). Открытый интервал может быть пустым, даже если а < б. Например, открытый интервал (1, 2) на целых числах пусто, поскольку нет целых чисел я такой, что 1 < я < 2.

В полуоткрытые интервалы [а, б) и (а, б] определяются аналогично.

Иногда определения расширяются, чтобы позволить а > б, и в этом случае интервал пуст.

Интервал я ограничено, если существуют элементы а и б из п такой, что я ⊆ [а, б]. Каждый интервал, который может быть представлен в обозначении интервалов, очевидно, ограничен, но обратное неверно. Например, пусть п = (0, 1) ∪ (1, 2) ∪ (2, 3) как подмножество действительные числа. Подмножество (1, 2) является ограниченным интервалом, но не имеет инфимум или же супремум в п, поэтому его нельзя записать в интервальной записи с использованием элементов п.

Посеть называется локально конечный если каждый ограниченный интервал конечен. Например, целые числа локально конечны по своему естественному порядку. Лексикографический порядок в декартовом произведении ℕ × не является локально конечным, поскольку (1, 2) ≤ (1, 3) ≤ (1, 4) ≤ (1, 5) ≤ ... ≤ (2, 1). Используя обозначение интервалов, свойство "а покрывается б"можно перефразировать эквивалентно как [а, б] = {а, б}.

Эту концепцию интервала в частичном порядке не следует путать с конкретным классом частичных порядков, известным как интервальные заказы.

Смотрите также

Примечания

  1. ^ Меррифилд, Ричард Э .; Симмонс, Говард Э. (1989). Топологические методы в химии. Нью-Йорк: Джон Вили и сыновья. стр.28. ISBN  0-471-83817-9. Получено 27 июля 2012. Частично упорядоченное множество удобно представить в виде Диаграмма Хассе...
  2. ^ Симовичи, Дэн А. и Джераба, Чабане (2008). «Частично заказанные наборы». Математические инструменты для интеллектуального анализа данных: теория множеств, частичные порядки, комбинаторика. Springer. ISBN  9781848002012.
  3. ^ Видеть General_relativity # Time_travel
  4. ^ Neggers, J .; Ким, Хи Сик (1998), «4.2 Порядок продуктов и лексикографический порядок», Базовые позы, World Scientific, стр. 62–63, ISBN  9789810235895
  5. ^ Davey, B.A .; Пристли, Х.А. (2002). Введение в решетки и порядок (Второе изд.). Нью-Йорк: Издательство Кембриджского университета. С. 17–18. ISBN  0-521-78451-4 - через Google Книги.
  6. ^ П. Р. Халмос (1974). Наивная теория множеств. Springer. п.82. ISBN  978-1-4757-1645-0.
  7. ^ Флашка, В .; Ježek, J .; Кепка, Т .; Кортелайнен, Дж. (2007). Транзитивные замыкания бинарных отношений I. Прага: Школа математики - Карлов университет физики. п. 1. Лемма 1.1 (iv). Обратите внимание, что этот источник называет асимметричные отношения «строго антисимметричными».
  8. ^ Davey, B.A .; Пристли, Х.А. (2002). «Карты между упорядоченными наборами». Введение в решетки и порядок (2-е изд.). Нью-Йорк: Издательство Кембриджского университета. С. 23–24. ISBN  0-521-78451-4. МИСТЕР  1902334..
  9. ^ Jech, Thomas (2008) [1973]. Аксиома выбора. Dover Publications. ISBN  978-0-486-46624-8.
  10. ^ Уорд, Л. Э. младший (1954). «Частично упорядоченные топологические пространства». Труды Американского математического общества. 5 (1): 144–161. Дои:10.1090 / S0002-9939-1954-0063016-5. HDL:10338.dmlcz / 101379.

Рекомендации

внешняя ссылка