Cent (музыка) - Cent (music)

Один цент по сравнению с полутоном на усеченном монохорд.

Октавы увеличиваются экспоненциально при измерении на линейной шкале частот (Гц).

Октавы равномерно распределены при измерении в логарифмической шкале (в центах).

В цент это логарифмический единица измерения, используемая для музыкальных интервалы. Двенадцатитонный ровный темперамент разделяет октава в 12 полутоны по 100 центов каждая. Обычно центы используются для обозначения небольших интервалов или для сравнения размеров сопоставимых интервалов в разных системы настройки На самом деле интервал в один цент слишком мал, чтобы его можно было различить между последовательными нотами.

Центов, как описано Александр Дж. Эллис, следуйте традиции измерения интервалов логарифмами, которая начиналась с Хуан Карамуэль и Лобковиц в 17 веке.^[1] Эллис решил основывать свои измерения на сотой части полутона, ¹²⁰⁰√2, в Роберт Холфорд Макдауэлл Босанкет предложение. Он провел обширные измерения музыкальных инструментов со всего мира, широко используя центы для составления отчетов и сравнения используемых шкал.^[2] и далее описал и использовал систему в своем издании 1875 г. Герман фон Гельмгольц с Об ощущениях тона. Это стало стандартным методом представления и сравнения музыкальных нот и интервалов.^[3]^[4]

Использовать

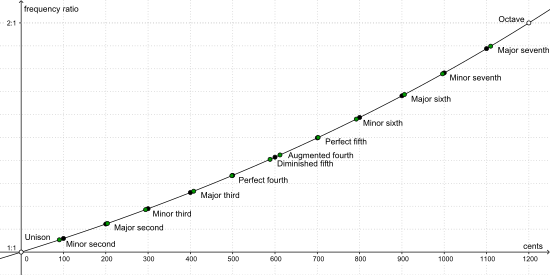
Сравнение уравновешенный (черный и Пифагорейский (зеленый) интервалы, показывающие соотношение между соотношением частот и значениями интервалов в центах.

Цент - это единица измерения отношения двух частот. An в равной степени сдержанный полутон (интервал между двумя соседними клавишами фортепиано) по определению составляет 100 центов. An октава - две ноты с соотношением частот 2: 1 - охватывают двенадцать полутонов и, следовательно, 1200 центов. Так как частота, увеличенная на один цент, просто умножается на это постоянное значение в процентах, а 1200 центов удваивают частоту, соотношение частот, разнесенных на один цент, точно равно 2^{¹⁄₁₂₀₀} = ¹²⁰⁰√2, то Корень 1200-й степени из 2, что примерно 1.0005777895.

Если знать частоты а и б двух банкнот, количество центов, измеряющих интервал от а к б можно рассчитать по следующей формуле (аналогичной определению децибела):

{ displaystyle n = 1200 cdot log _ {2} left ({ frac {b} {a}} right)}

Точно так же, если кто-то знает записку а и число п центов в интервале от а к б, тогда б можно рассчитать по:

{ displaystyle b = a times 2 ^ { frac {n} {1200}}}

Для сравнения различных систем настройки преобразуйте различные размеры интервалов в центы. Например, в просто интонация, большая треть представлена соотношением частот 5: 4. Применение формулы вверху показывает, что это около 386 центов. Эквивалентный интервал на фортепиано с равномерным темпом будет 400 центов. Разница в 14 центов составляет примерно седьмые полутона, легко слышимая.

Кусочно-линейная аппроксимация

В качестве Икс увеличивается с 0 до¹⁄₁₂, функция 2^Икс возрастает почти линейно от 1.00000 к 1.05946. Таким образом, экспоненциальную шкалу в процентах можно точно аппроксимировать как кусочно-линейная функция что численно правильно на полутонах. То есть, п центов за п от 0 до 100 может быть приблизительно равно 1 +0.0005946п вместо 2^{^п⁄₁₂₀₀}. Округленная ошибка равна нулю, когда п составляет 0 или 100 и составляет около 0,72 цента, когда п 50, где правильное значение 2^¹⁄₂₄ = 1.02930 приблизительно 1 +0.0005946 × 50 = 1,02973. Эта ошибка намного ниже того, что может слышать человек, что делает эту кусочно-линейную аппроксимацию адекватной для большинства практических целей.

Человеческое восприятие

Формы волны унисона (синий) и цента (красный) почти неразличимы.

Трудно установить, сколько центов воспринимается человеком; эта точность сильно варьируется от человека к человеку. Один автор заявил, что люди могут различать разницу в высоте тона около 5–6 центов.^[5] Порог ощутимого, технически известный как просто заметная разница (JND), также изменяется в зависимости от частоты, амплитуды и тембр. В одном исследовании изменения качества звука снизили способность студентов-музыкантов распознавать расстроенные высоты тона, отклоняющиеся от их соответствующих значений на ± 12 центов.^[6] Также было установлено, что усиление тонального контекста позволяет слушателям более точно судить о высоте звука.^[7] «В то время как интервалы менее нескольких центов незаметны для человеческого уха в мелодическом контексте, в гармонии очень маленькие изменения могут вызвать большие изменения в ударах и резкости аккордов».^[8]

При прослушивании питчей с вибрато, есть свидетельства того, что люди воспринимают среднюю частоту как центр звука.^[9] Одно исследование современных исполнений Шуберта Аве Мария обнаружили, что диапазон вибрато обычно находится в диапазоне от ± 34 до ± 123 центов со средним значением ± 71 цент, и отметили более высокую вариацию в Верди Оперные арии.^[10]

Нормальные взрослые люди могут очень надежно распознавать разницу в высоте звука всего на 25 центов. Взрослые с амусия однако у них возникают проблемы с распознаванием разницы менее 100 центов, а иногда возникают проблемы с этими или большими интервалами.^[11]

Centitone

А сентитон (также Iring) это музыкальный интервал (2^{¹⁄₆₀₀}) равный двум центам (2^{²⁄₁₂₀₀})^[12] предлагается в качестве единицы измерения (Играть в (помощь ·Информация )) от Widogast Iring in Die Reine Stimmung in der Musik (1898) как 600 шагов на октава а позже Джозеф Яссер в Теория эволюции тональности (1932) как 100 шагов на равноправный весь тон.

Айринг заметила, что Grad / Werckmeister (1,96 цента, 12 за Пифагорейская запятая ) и раскол (1,95 цента) примерно одинаковы (≈ 614 шагов на октаву), и оба могут быть приблизительно 600 шагов на октаву (2 цента).^[13] Ясер продвигал децитон, сентитон и миллитон (10, 100 и 1000 шагов на весь тон = 60, 600 и 6000 шагов на октаву = 20, 2 и 0,2 цента).^[14]^[15]

Например: равномерный темперированный идеальный квинт = 700 центов = 175,6 Savarts = 583.3 миллиоктавы = 350 сантитонов.^[16]

Центитоны	Центов
1 сентитон	2 цента
0,5 сентитона	1 цент
2^{¹⁄₆₀₀}	2^{²⁄₁₂₀₀}
50 на полутон	100 на полутон
100 на весь тон	200 на весь тон

Звуковые файлы

Следующие аудиофайлы воспроизводятся с разными интервалами. В каждом случае первая сыгранная нота - это средняя C. Следующая нота острее, чем C на заданное значение в центах. Наконец, две ноты играются одновременно.

Обратите внимание, что JND для разницы в высоте тона составляет 5–6 центов. При игре по отдельности ноты могут не иметь слышимой разницы, но когда они играются вместе, избиение может быть слышен (например, если играют среднюю до и ноту на 10 центов выше). В любой конкретный момент две формы волны усиливают или нейтрализуют друг друга в большей или меньшей степени, в зависимости от их мгновенного действия. фаза отношение. Настройщик пианино может проверить точность настройки, отсчитывая удары при одновременном звучании двух струн.

Играть в середине C и на 1 цент выше (помощь ·Информация ), частота биений = 0,16 Гц
Играть в середине C и 10,06 цента выше (помощь ·Информация ), частота биений = 1,53 Гц
Играть в середине C и 25 центов выше (помощь ·Информация ), частота биений = 3,81 Гц