Сплит-комплексное число - Split-complex number

«Двойной номер» перенаправляется сюда. Формат номера компьютера см. формат с плавающей запятой двойной точности.

В абстрактная алгебра, а разделить комплексное число (или же гиперболическое число, также номер недоумения, двойной номер) имеет два настоящий номер составные части Икс и у, и написано z = Икс + у j, куда j² = 1. В сопрягать из z является z^∗ = Икс − у j. С j² = 1, произведение числа z со своим конъюгатом zz^∗ = Икс² − у², изотропная квадратичная форма, N(z) = Икс² − у².

Коллекция D всех разделенных комплексных чисел z = Икс + у j за Икс, у ∈ р образует алгебра над полем действительных чисел. Два сплит-комплексных числа ш и z есть продукт wz это удовлетворяет N(wz) = N(ш)N(z). Эта композиция N над произведением алгебры делает (D, +, ×, *) а композиционная алгебра.

Аналогичная алгебра, основанная на р² и покомпонентные операции сложения и умножения, (р², +, ×, ху), куда ху это квадратичная форма на р², также образует квадратичное пространство. В изоморфизм колец

${\displaystyle {\begin{aligned}D&\to \mathbb {R} ^{2}\\x+yj&\mapsto (x+y,x-y)\end{aligned}}}$

связывает пропорциональные квадратичные формы, но отображение нет ан изометрия поскольку мультипликативное тождество (1, 1) р² находится на расстоянии √2 от 0, который нормирован в D.

У разделенных комплексных чисел есть много других имен; видеть § Синонимы ниже. См. Статью Переменная двигателя для функций расщепленного комплексного числа.

Определение

А расщепленное комплексное число - это упорядоченная пара действительных чисел, записанная в виде

${\displaystyle z=x+jy}$

куда Икс и у находятся действительные числа и количество j удовлетворяет

${\displaystyle j^{2}=+1}$

Выбор ${\displaystyle j^{2}=-1}$ приводит к сложные числа. Именно это изменение знака отличает расщепленные комплексные числа от обычных комплексных. Количество j здесь не действительное число, а независимая величина.

Собрание всего такого z называется расщепленная комплексная плоскость. Добавление и умножение разделенных комплексных чисел определяются

${\displaystyle {\begin{aligned}(x+jy)+(u+jv)&=(x+u)+j(y+v)\\(x+jy)(u+jv)&=(xu+yv)+j(xv+yu).\end{aligned}}}$

Это умножение коммутативный, ассоциативный и распределяет сверх сложения.

Сопряженная, модульная и билинейная форма

Как и для комплексных чисел, можно определить понятие сплит-комплексное сопряжение. Если

${\displaystyle z=x+jy}$

конъюгат z определяется как

${\displaystyle z^{*}=x-jy.}$

Сопряжение обладает свойствами, аналогичными обычному комплексно сопряженному. А именно,

${\displaystyle {\begin{aligned}(z+w)^{*}&=z^{*}+w^{*}\\(zw)^{*}&=z^{*}w^{*}\\\left(z^{*}\right)^{*}&=z.\end{aligned}}}$

Эти три свойства подразумевают, что комплексно-расщепляемое сопряжение является автоморфизм из порядок 2.

В модуль расщепленного комплексного числа z = Икс + j у дается изотропная квадратичная форма

${\displaystyle \lVert z\rVert =zz^{*}=z^{*}z=x^{2}-y^{2}.}$

Он имеет композиционная алгебра свойство:

${\displaystyle \lVert zw\rVert =\lVert z\rVert \lVert w\rVert .}$

Однако эта квадратичная форма не положительно определенный а скорее имеет подпись (1, −1), поэтому модуль нет а норма.

Связанный билинейная форма дан кем-то

${\displaystyle \langle z,w\rangle =\operatorname {Re} \left(zw^{*}\right)=\operatorname {Re} \left(z^{*}w\right)=xu-yv,}$

куда z = Икс + j у и ш = ты + j v. Другое выражение для модуля тогда

${\displaystyle \lVert z\rVert =\langle z,z\rangle .}$

Поскольку она не является положительно определенной, эта билинейная форма не является внутренний продукт; тем не менее, билинейную форму часто называют неопределенный внутренний продукт. Подобное злоупотребление языком относится к модулю как к норме.

Сплит-комплексное число обратимо если и только если его модуль отличен от нуля (${\displaystyle \lVert z\rVert \neq 0}$), таким образом Икс ± j Икс не имеют обратного. В мультипликативный обратный обратимого элемента задается формулой

${\displaystyle z^{-1}={\frac {z^{*}}{\lVert z\rVert }}.}$

Необратимые расщепляемые комплексные числа называются нулевые векторы. Это все в форме (а ± j а) для какого-то реального числа а.

Диагональное основание

Есть два нетривиальных идемпотентные элементы данный е = (1 − j)/2 и е^∗ = (1 + j)/2. Напомним, что идемпотент означает, что ее = е и е^∗е^∗ = е^∗. Оба эти элемента равны нулю:

${\displaystyle \lVert e\rVert =\lVert e^{*}\rVert =e^{*}e=0.}$

Часто удобно использовать е и е^∗ в качестве альтернативы основа для расщепленной комплексной плоскости. Эта основа называется диагональное основание или же нулевая основа. Сплит-комплексное число z можно записать в нулевом базисе как

${\displaystyle z=x+jy=(x-y)e+(x+y)e^{*}.}$

Если обозначить число z = ае + быть^∗ для реальных чисел а и б к (а, б), то расщепляемое комплексное умножение дается формулой

${\displaystyle \left(a_{1},b_{1}\right)\left(a_{2},b_{2}\right)=\left(a_{1}a_{2},b_{1}b_{2})\right.}$

Исходя из этого, становится ясно, что расщепляемые комплексные числа кольцевой изоморфный на прямую сумму р ⊕ р со сложением и умножением, определенными попарно.

Сплит-комплексно-сопряженный в диагональном базисе равен

${\displaystyle (a,b)^{*}=(b,a)}$

и модуль на

${\displaystyle \lVert (a,b)\rVert =ab.}$

Хотя лежат в том же классе изоморфизма в категория колец, разделенная комплексная плоскость и прямая сумма двух вещественных линий различаются по своему расположению в Декартова плоскость. Изоморфизм как планарное отображение состоит из поворота против часовой стрелки на 45 ° и расширение к √2. Расширение, в частности, иногда вызывает путаницу в связи с областями гиперболический сектор. В самом деле, гиперболический угол соответствует площадь сектора в р ⊕ р плоскость с ее "единичной окружностью", заданной {(а, б) ∈ р ⊕ р : ab = 1}. Сжатый «единичный круг» {cosh а + j грех а : а ∈ р ⊕ р} разделенно-комплексной плоскости имеет только половина площади в пролете соответствующего гиперболического сектора. Такая путаница может сохраняться, если геометрия плоскости расщепленного комплекса не отличается от геометрии плоскости р ⊕ р.

Геометрия

  Гипербола единиц с ‖z‖ = 1,
  сопряженная гипербола с ‖z‖ = −1, и
  асимптоты ‖z‖ = 0.

Двумерный реальный векторное пространство с внутренним произведением Минковского называется (1 + 1)-размерный Пространство Минковского, часто обозначаемый р^1,1. Столько же геометрия евклидовой плоскости р² можно описать комплексными числами, геометрия плоскости Минковского р^1,1 можно описать комплексными числами.

Набор точек

${\displaystyle \left\{z:\lVert z\rVert =a^{2}\right\}}$

это гипербола для каждого ненулевого а в р. Гипербола состоит из правой и левой ветвей, проходящих через (а, 0) и (−а, 0). Дело а = 1 называется гипербола единиц. Сопряженная гипербола задается формулой

${\displaystyle \left\{z:\lVert z\rVert =-a^{2}\right\}}$

с прохождением верхней и нижней ветви (0, а) и (0, −а). Гипербола и сопряженная гипербола разделены двумя диагональными асимптоты которые образуют набор нулевых элементов:

${\displaystyle \left\{z:\lVert z\rVert =0\right\}.}$

Эти две строки (иногда называемые нулевой конус) находятся перпендикуляр в р² и имеют наклон ± 1.

Сплит-комплексные числа z и ш как говорят гиперболо-ортогональный если ⟨z, ш⟩ = 0. Хотя это условие аналогично обычной ортогональности, в частности, в обычной арифметике комплексных чисел, это условие более тонкое. Он составляет основу одновременная гиперплоскость концепция в пространстве-времени.

Аналог Формула Эйлера для разделенных комплексных чисел

${\displaystyle \exp(j\theta )=\cosh(\theta )+j\sinh(\theta ).\,}$

Это можно вывести из степенной ряд расширение, используя тот факт, что шиш имеет только четные полномочия, в то время как для грех обладает странными способностями. Для всех реальных значений гиперболический угол θ расщепленное комплексное число λ = ехр (jθ) имеет норму 1 и лежит на правой ветви единичной гиперболы. Такие числа, как λ, были названы гиперболические версоры.

Поскольку λ имеет модуль 1, умножение любого расщепляемого комплексного числа z к λ сохраняет модуль z и представляет собой гиперболическое вращение (также называемый Повышение лоренца или сжатие ). Умножение на λ сохраняет геометрическую структуру, принимая гиперболы на себя, а нулевой конус - на себя.

Набор всех преобразований разделенной комплексной плоскости, которые сохраняют модуль (или, что то же самое, внутреннее произведение), образует группа называется обобщенная ортогональная группа О (1, 1). Эта группа состоит из гиперболических вращений, образующих подгруппа обозначенный ТАК⁺(1, 1)в сочетании с четырьмя дискретный размышления данный

${\displaystyle z\mapsto \pm z}$ и ${\displaystyle z\mapsto \pm z^{*}.}$

Экспоненциальная карта

${\displaystyle \exp \colon (\mathbb {R} ,+)\to \mathrm {SO} ^{+}(1,1)}$

отправка θ к повороту на exp (jθ) это групповой изоморфизм поскольку применяется обычная экспоненциальная формула:

${\displaystyle e^{j(\theta +\phi )}=e^{j\theta }e^{j\phi }.\,}$

Если комплексное число z не лежит на одной из диагоналей, то z имеет полярное разложение.

Алгебраические свойства

В абстрактная алгебра слагаемые, комплексные числа с разбиением можно описать как частное из кольцо многочленов р[Икс] посредством идеальный генерируется многочлен Икс² − 1,

р[Икс]/(Икс² − 1).

Образ Икс в частном - "мнимая" единица j. Из этого описания ясно, что расщепленные комплексные числа образуют коммутативное кольцо с характеристика 0. Более того, если мы определим скалярное умножение очевидным образом, расщепленные комплексные числа образуют коммутативную и ассоциативная алгебра измерения два над реалами. Алгебра нет а алгебра с делением или же поле поскольку нулевые элементы необратимы. Все ненулевые нулевые элементы являются делители нуля.

Поскольку сложение и умножение являются непрерывными операциями по отношению к обычной топологии плоскости, расщепленные комплексные числа образуют топологическое кольцо.

Алгебра расщепляемых комплексных чисел образует композиционная алгебра поскольку

${\displaystyle \lVert zw\rVert =\lVert z\rVert \lVert w\rVert }$ для любых номеров z и ш.

Из определения очевидно, что кольцо расщепляемых комплексных чисел изоморфно кольцу групповое кольцо р[C₂] из циклическая группа C₂ над реальными числами р.

Матричные представления

Комплексные числа с разбиением легко представить как матрицы. Сплит-комплексное число

${\displaystyle z=x+jy}$

можно представить матрицей

${\displaystyle z\mapsto {\begin{pmatrix}x&y\\y&x\end{pmatrix}}.}$

Сложение и умножение комплексных чисел с разбиением затем задаются сложением и умножением матриц. Модуль упругости z дается детерминант соответствующей матрицы. В этом представлении расщепленное комплексное сопряжение соответствует умножению с обеих сторон на матрицу

${\displaystyle C={\begin{pmatrix}1&0\\0&-1\end{pmatrix}}.}$

Для любого реального числа а, гиперболическое вращение на гиперболический угол а соответствует умножению на матрицу

${\displaystyle {\begin{pmatrix}\cosh a&\sinh a\\\sinh a&\cosh a\end{pmatrix}}.}$

Этот коммутативная диаграмма связывает действие гиперболического версора на D сжать отображение σ, примененное к R²

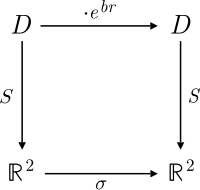
Диагональный базис для плоскости разделенных комплексных чисел может быть вызван с помощью упорядоченной пары (Икс, у) за ${\displaystyle z=x+jy}$ и составление карты

${\displaystyle (u,v)=(x,y){\begin{pmatrix}1&1\\1&-1\end{pmatrix}}=(x,y)S.}$

Теперь квадратичная форма ${\displaystyle uv=(x+y)(x-y)=x^{2}-y^{2}.}$ Более того,

${\displaystyle (\cosh a,\sinh a){\begin{pmatrix}1&1\\1&-1\end{pmatrix}}=\left(e^{a},e^{-a}\right)}$

так что двое параметризованный гиперболы приведены в соответствие с S.

В действие из гиперболический версор ${\displaystyle e^{bj}\!}$ то соответствует при этом линейном преобразовании сжатие

${\displaystyle \sigma :(u,v)\mapsto \left(ru,{\frac {v}{r}}\right),\quad r=e^{b}.}$

Обратите внимание, что в контексте 2 × 2 вещественные матрицы на самом деле существует множество различных представлений комплексных чисел с разбиением на части. Приведенное выше диагональное представление представляет собой Иорданская каноническая форма матричного представления расщепленных комплексных чисел. Для разделенного комплексного числа z = (Икс, у) задается следующим матричным представлением:

${\displaystyle Z={\begin{pmatrix}x&y\\y&x\end{pmatrix}}}$

его каноническая форма Иордании определяется следующим образом:

${\displaystyle J_{z}={\begin{pmatrix}x+y&0\\0&x-y\end{pmatrix}},}$

куда ${\displaystyle Z=SJ_{z}S^{-1}\ ,}$ и

${\displaystyle S={\begin{pmatrix}1&-1\\1&1\end{pmatrix}}.}$

История

Использование разделенных комплексных чисел восходит к 1848 году, когда Джеймс Кокл показал его тессарины.^[1] Уильям Кингдон Клиффорд использовали комплексные числа с разделением для представления суммы спинов. Клиффорд ввел использование разделенных комплексных чисел в качестве коэффициентов в алгебре кватернионов, которая теперь называется сплит-бикватернионы. Он назвал его элементы «двигателями», термин, параллельный действию «ротора» обычного комплексного числа, взятого из круговая группа. Продолжая аналогию, функции моторная переменная отличие от функций обычного комплексная переменная.

С конца двадцатого века сложное умножение с расщеплением обычно рассматривалось как Повышение лоренца из пространство-время самолет.^{[2][3][4][5][6][7]} В этой модели число z = Икс + у j представляет собой событие в пространственно-временной плоскости, где Икс измеряется в наносекундах и у в Ноги Мермина. Будущее соответствует квадранту событий {z : |у| < Икс}, который имеет расщепленное комплексное полярное разложение ${\displaystyle z=\rho e^{aj}\!}$. Модель говорит, что z можно добраться из исходной точки, введя точка зрения из быстрота а и жду ρ наносекунды. Расщепленное комплексное уравнение

${\displaystyle e^{aj}\ e^{bj}=e^{(a+b)j}}$

выражение произведений на единичной гиперболе иллюстрирует аддитивность быстрот для коллинеарных скоростей. Одновременность событий зависит от быстроты а;

${\displaystyle \lbrace z=\sigma je^{aj}:\sigma \in \mathbb {R} \rbrace }$

это линия событий, одновременная с началом в системе отсчета с быстротой а.

Два события z и ш находятся гиперболо-ортогональный когда z^∗ш + zw^∗ = 0. Канонические события exp (эй) и j ехр (эй) являются гиперболическими ортогональными и лежат на осях системы отсчета, в которой события, одновременные с началом координат, пропорциональны j ехр (эй).

В 1933 г. Макс Зорн использовал сплит-октонионы и отметил композиционная алгебра свойство. Он понял, что Конструкция Кэли-Диксона, используемый для создания алгебр с делением, может быть изменен (с фактором гамма (γ)) для построения других композиционных алгебр, включая расщепленные октонионы. Его новаторство было увековечено Адриан Альберт, Ричард Д. Шафер и другие.^[8] Гамма-фактор с ℝ в качестве базового поля строит расщепляемые комплексные числа как композиционную алгебру. Обзор Альберта для Математические обзоры, Н. Х. Маккой писал, что было «введение некоторых новых алгебр порядка 2.^е над F обобщающие алгебры Кэли – Диксона ".^[9] Принимая F = ℝ и е = 1 соответствует алгебре данной статьи.

В 1935 г. Дж. К. Винно и А. Дураньона-и-Ведиа разработали комплексную геометрическую алгебру и теорию функций в четырех статьях в Contribución a las Ciencias Físicas y Matemáticas, Национальный университет Ла-Платы, República Argentina (на испанском). Эти разъяснительные и педагогические эссе представляют предмет для широкой оценки.^[10]

В 1941 году Э.Ф. Аллен применил геометрическую арифметику с расщепленными комплексами, 9-точечная гипербола треугольника, вписанного вzz^∗ = 1.^[11]

В 1956 году Мечислав Вармус опубликовал «Исчисление приближений» в Bulletin de l’Académie Polonaise des Sciences (см. ссылку в Справочнике). Он разработал две алгебраические системы, каждую из которых он назвал «приближенными числами», вторая из которых образует действительную алгебру.^[12] Д. Х. Лемер просмотрел статью в Математические обзоры и заметил, что эта вторая система изоморфна «гиперболическим комплексным» числам, предмету данной статьи.

В 1961 году Вармус продолжил свое изложение, ссылаясь на компоненты приблизительного числа как на середину и радиус обозначенного интервала.

Синонимы

Разные авторы использовали множество названий комплексных чисел с разбиением на части. Некоторые из них включают:

• (настоящий) тессарины, Джеймс Кокл (1848)
• (алгебраический) моторы, W.K. Клиффорд (1882)
• гиперболические комплексные числа, Ж.К.Вино (1935)
• двумерные числа, У. Бенчивенга (1946)
• приблизительные цифры, Warmus (1956), для использования в интервальный анализ
• контркомплекс или же гиперболический числа из музеев гиперчислов
• двойные числа, И. М. Яглом (1968), Кантор и Солодовников (1989), Hazewinkel (1990), Руни (2014)
• анормально-комплексные числа, В. Бенц (1973)
• недоуменные числа, П. Фьелстад (1986) и Poodiack & LeClair (2009)
• Числа Лоренца, Ф. Харви (1990)
• гиперболические числа, Г. Собчик (1995)
• паракомплексные числа, Кручану, Фортуни и Гадеа (1996)
• полусложные числа, Ф. Антонуччо (1994)
• разделить бинарионы, К. МакКриммон (2004)
• разделенные комплексные числа, Б. Розенфельд (1997)^[13]
• пространственно-временные числа, Н. Борота (2000)
• Номера исследований, П. Лунесто (2001)
• двакомплексных числа, С. Олариу (2002)

Сплит-комплексные числа и их многомерные родственники (сплит-кватернионы / кокватернионы и сплит-октонионы ) иногда назывались "числами Музея", поскольку они являются подмножеством программы гиперчислов, разработанной Шарль Мусес.

Смотрите также

• Пространство Минковского
• Сплит-кватернион
• Номер гиперкомплекса

Рекомендации

1. Джеймс Кокл (1849) О новом воображаемом в алгебре 34:37–47, Лондон-Эдинбург-Дублинский философский журнал (3) 33: 435–9, ссылка с Библиотека наследия биоразнообразия.
2. Франческо Антонуччо (1994) Полусложный анализ и математическая физика
3. Ф. Катони, Д. Боккалетти, Р. Канната, В. Катони, Э. Ничелатти, П. Зампетти. (2008) Математика пространства-времени Минковского, Birkhäuser Verlag, Базель. Глава 4: Тригонометрия на плоскости Минковского. ISBN  978-3-7643-8613-9.
4. Франческо Катони; Дино Боккалетти; Роберто Канната; Винченцо Катони; Паоло Зампетти (2011). «Глава 2: Гиперболические числа». Геометрия пространства-времени Минковского. Springer Science & Business Media. ISBN  978-3-642-17977-8.
5. Фьельштадт, П. (1986) "Расширение специальной теории относительности с помощью загадочных чисел ", Американский журнал физики 54 :416.
6. Луи Кауфман (1985) "Преобразования в специальной теории относительности", Международный журнал теоретической физики 24:223–36.
7. Собчик, Г. (1995) Плоскость гиперболических чисел, также опубликовано в Журнал математики колледжа 26:268–80.
8. Роберт Б. Браун (1967)Об обобщенных алгебрах Кэли-Диксона, Тихоокеанский математический журнал 20 (3): 415–22, ссылка с Проект Евклид.
9. Н. Х. Маккой (1942) Обзор книги А.А. Квадратичные формы, допускающие композицию. Альберт, Математические обзоры #0006140
10. Винно, Ж. (1935) "Sobre el numero complejo hiperbolico y su relacion con la geometria de Borel", Contribucion al Estudio de las Ciencias Fisicas y Matematicas, Национальный университет де ла Плата, Республика Аргентина
11. Аллен, Э.Ф. (1941) "На треугольнике, вписанном в прямоугольную гиперболу", Американский математический ежемесячный журнал 48(10): 675–681
12. М. Вармус (1956) «Исчисление приближений», Bulletin de l'Académie Polonaise des Sciences, Vol. 4, № 5, с. 253–257, МИСТЕР0081372
13. Розенфельд, Б. (1997) Геометрия групп Ли, стр.30, Kluwer Academic Publishers ISBN  0-7923-4390-5

• Бенчивенга, Ульдрико (1946) "Sulla rappresentazione geometrya delle algebre doppie dotate di modulo", Atti della Reale Accademia delle Scienze e Belle-Lettere di Napoli, Сер (3) т.2 No7. МИСТЕР0021123.
• Уолтер Бенц (1973) Vorlesungen uber Geometrie der Algebren, Springer
• Н. А. Борота, Э. Флорес и Т. Дж. Ослер (2000) "Пространственно-временные числа - легкий путь", Математика и компьютерное образование 34: 159–168.
• Н. А. Борота и Т. Дж. Ослер (2002) "Функции пространственно-временной переменной", Математика и компьютерное образование 36: 231–239.
• К. Кармоди, (1988) "Круглые и гиперболические кватернионы, октонионы и седенионы", Appl. Математика. Comput. 28: 47–72.
• К. Кармоди, (1997) "Круговые и гиперболические кватернионы, октонионы и седенионы - дальнейшие результаты", Appl. Математика. Comput. 84: 27–48.
• Уильям Кингдон Клиффорд (1882) Математические работы, Редактор A. W. Tucker, стр. 392, "Дополнительные сведения о бикватернионах"
• В.Кручану, П. Фортуни и П.М. Гадеа (1996) Обзор паракомплексной геометрии, Журнал математики Роки-Маунтин 26 (1): 83–115, ссылка с Проект Евклид.
• Де Бур, Р. (1987) "Также известный как список недоуменных чисел", Американский журнал физики 55(4):296.
• Энтони А. Харкин и Джозеф Б. Харкин (2004) Геометрия обобщенных комплексных чисел, Математический журнал 77(2):118–29.
• Ф. Риз Харви. Спиноры и калибровки. Academic Press, Сан-Диего. 1990 г. ISBN  0-12-329650-1. Содержит описание нормированных алгебр с неопределенной сигнатурой, включая числа Лоренца.
• Хазевинкль, М. (1994) «Двойные и двойственные числа», Энциклопедия математики, Советский / AMS / Kluwer, Dordrect.
• Кевин МакКриммон (2004) Вкус иорданских алгебр, стр 66, 157, Universitext, Springer ISBN  0-387-95447-3 МИСТЕР2014924
• C. Musès, "Прикладные гиперчисла: вычислительные концепции", Appl. Математика. Comput. 3 (1977) 211–226.
• C. Musès, "Hypernumbers II - Дальнейшие концепции и вычислительные приложения", Appl. Математика. Comput. 4 (1978) 45–66.
• Олариу, Сильвиу (2002) Комплексные числа в N измерениях, Глава 1: Гиперболические комплексные числа в двух измерениях, страницы 1–16, North-Holland Mathematics Studies # 190, Эльзевир ISBN  0-444-51123-7.
• Poodiack, Роберт Д. и Кевин Дж. Леклер (2009) "Основные теоремы алгебры для недоумений", Математический журнал колледжа 40(5):322–35.
• Исаак Яглом (1968) Комплексные числа в геометрии, перевод Э. Примроуза с русского оригинала 1963 г., Академическая пресса С. 18–20.
• Дж. Руни (2014). «Обобщенные комплексные числа в механике». В Марко Чеккарелли и Викторе А. Глазунове (ред.). Успехи теории и практики роботов и манипуляторов: материалы Romansy 2014 XX симпозиум CISM-IFToMM по теории и практике роботов и манипуляторов. Механизмы и машиноведение. 22. Springer. С. 55–62. Дои:10.1007/978-3-319-07058-2_7. ISBN  978-3-319-07058-2.