Сеть Хопфилда - Hopfield network

А Сеть Хопфилда (или же Модель Изинга нейронной сети или же Модель Изинга – Ленца – Литтла) является формой повторяющийся искусственная нейронная сеть популяризируется Джон Хопфилд в 1982 г., но описанный ранее Литтлом в 1974 г. на основе Эрнст Изинг работает с Вильгельм Ленц.^[1][2] Сети Хопфилда служат контентно-адресная ("ассоциативная") память системы с двоичный порог узлы. Они гарантированно сходятся к местный минимум и, следовательно, может сходиться к ложному шаблону (неправильный локальный минимум), а не к сохраненному шаблону (ожидаемому локальному минимуму)^{[нужна цитата ]}. Сети Хопфилда также предоставляют модель для понимания человеческой памяти.^[3][4]

Происхождение

Модель Изинга нейронной сети в качестве модели памяти впервые предлагается^{[нужна цитата ]} В. А. Литтл из Стэндфордский Университет в 1974 г. в своей статье «Существование устойчивых состояний в мозге».

Структура

Сетка Хопфилда с четырьмя звеньями

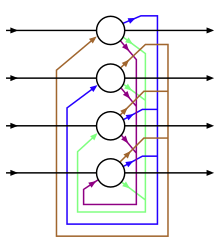
Единицы в сетях Хопфилда являются бинарными пороговыми единицами, то есть единицы принимают только два разных значения для своих состояний, и значение определяется тем, превышает ли вход единиц их пороговое значение. Сети Хопфилда обычно имеют единицы, принимающие значения 1 или -1, и это соглашение будет использоваться на протяжении всей статьи. Однако в другой литературе могут использоваться единицы, принимающие значения 0 и 1.

Каждая пара единиц я и j в сети Хопфилда есть соединение, которое описывается весом связности ${\displaystyle w_{ij}}$. В этом смысле сеть Хопфилда можно формально описать как полный неориентированный граф ${\displaystyle G=\langle V,f\rangle }$, куда ${\displaystyle V}$ это набор Нейроны Маккаллоха – Питтса и ${\displaystyle f:V^{2}\rightarrow \mathbb {R} }$ - это функция, которая связывает пары единиц с реальным значением, весом связности.

Соединения в сети Хопфилда обычно имеют следующие ограничения:

• ${\displaystyle w_{ii}=0,\forall i}$ (никакая единица не связана сама с собой)
• ${\displaystyle w_{ij}=w_{ji},\forall i,j}$ (соединения симметричны)

Ограничение, что веса являются симметричными, гарантирует, что функция энергии монотонно убывает при соблюдении правил активации.^[5] Сеть с асимметричными весами может демонстрировать периодическое или хаотическое поведение; однако Хопфилд обнаружил, что это поведение ограничено относительно небольшими частями фазового пространства и не ухудшает способность сети действовать как ассоциативная система памяти с адресацией по содержанию.

Обновление

Обновление одного блока (узла на графике, имитирующем искусственный нейрон) в сети Хопфилда выполняется по следующему правилу:

${\displaystyle s_{i}\leftarrow \left\{{\begin{array}{ll}+1&{\mbox{if }}\sum _{j}{w_{ij}s_{j}}\geq \theta _{i},\\-1&{\mbox{otherwise.}}\end{array}}\right.}$

куда:

• ${\displaystyle w_{ij}}$ - сила веса соединения от единицы j к единице i (вес соединения).
• ${\displaystyle s_{i}}$ состояние i-го агрегата.
• ${\displaystyle \theta _{i}}$ является порогом единицы i.

Обновления в сети Хопфилда могут выполняться двумя разными способами:

• Асинхронный: Одновременно обновляется только один модуль. Этот отряд можно выбрать случайным образом или задать заранее определенный порядок с самого начала.
• Синхронный: Все объекты обновляются одновременно. Для этого требуются центральные часы в системе, чтобы поддерживать синхронизацию. Некоторые считают этот метод менее реалистичным из-за отсутствия наблюдаемых глобальных часов, влияющих на аналогичные представляющие интерес биологические или физические системы.

Нейроны «притягивают или отталкивают друг друга» в пространстве состояний

Вес между двумя единицами оказывает сильное влияние на значения нейронов. Учитывайте вес соединения ${\displaystyle w_{ij}}$ между двумя нейронами i и j. Если ${\displaystyle w_{ij}>0}$, правило обновления подразумевает, что:

• когда ${\displaystyle s_{j}=1}$, вклад j во взвешенную сумму положительный. Таким образом, ${\displaystyle s_{i}}$ притягивается j к своему значению ${\displaystyle s_{i}=1}$
• когда ${\displaystyle s_{j}=-1}$, вклад j во взвешенную сумму отрицательный. Затем снова, ${\displaystyle s_{i}}$ подталкивается j к его значению ${\displaystyle s_{i}=-1}$

Таким образом, значения нейронов i и j сойдутся, если вес между ними положительный. Точно так же они будут расходиться, если вес отрицательный.

Принципы работы дискретных и непрерывных сетей Хопфилда

Брук пролил свет на поведение нейрона в дискретной сети Хопфилда, доказав его конвергенцию в своей статье 1990 года.^[6] Последующая статья ^[7] далее исследовал поведение любого нейрона в сетях Хопфилда как с дискретным, так и с непрерывным временем, когда соответствующая функция энергии минимизируется в процессе оптимизации. Брук показывает^[6] этот нейрон j меняет свое состояние если и только если это дополнительно уменьшает следующие предвзятый псевдорез. Дискретная сеть Хопфилда минимизирует следующие предвзятый псевдорез ^[7] для синаптической весовой матрицы сети Хопфилда.

${\displaystyle J_{pseudo-cut}(k)=\sum _{i\in C_{1}(k)}\sum _{j\in C_{2}(k)}w_{ij}+\sum _{j\in C_{1}(k)}{\theta _{j}}}$

куда ${\displaystyle C_{1}(k)}$ и ${\displaystyle C_{2}(k)}$ представляет собой набор нейронов, которые имеют -1 и +1, соответственно, в момент времени ${\displaystyle k}$. Для получения дополнительной информации см. Недавнюю статью.^[7]

В дискретное время Hopfield Network всегда сводит к минимуму точно следующие псевдо-резать   (^[6] , ^[7])

${\displaystyle U(k)=\sum _{i=1}^{N}\sum _{j=1}^{N}w_{ij}(s_{i}(k)-s_{j}(k))^{2}+2\sum _{j=1}^{N}{\theta _{j}}s_{j}(k)}$

Непрерывное время Сеть Хопфилда всегда сводит к минимуму ан верхняя граница к следующему утяжеленный разрез  ^[7]

${\displaystyle V(t)=\sum _{i=1}^{N}\sum _{j=1}^{N}w_{ij}({f(s_{i}(t))}-f(s_{j}(t))^{2}+2\sum _{j=1}^{N}{\theta _{j}}{f(s_{j}(t))}}$

куда ${\displaystyle f(.)}$ сигмоидальная функция с нулевым центром.

С другой стороны, сложная сеть Хопфилда обычно имеет тенденцию свести к минимуму так называемые вырезанный из тени комплексной матрицы весов сети.^[8]

Энергия

Энергетический ландшафт сети Хопфилда, выделяющий текущее состояние сети (в гору), состояние аттрактора, к которому она в конечном итоге сойдется, минимальный уровень энергии и область притяжения, заштрихованная зеленым. Обратите внимание на то, что обновление сети Hopfield Network всегда идет на спад в Energy.

Сети Хопфилда имеют скалярное значение, связанное с каждым состоянием сети, называемое «энергией» E сети, где:

${\displaystyle E=-{\frac {1}{2}}\sum _{i,j}{w_{ij}{s_{i}}{s_{j}}}+\sum _{i}{\theta _{i}}{s_{i}}}$

Это количество называется «энергией», потому что оно либо уменьшается, либо остается неизменным при обновлении сетевых модулей. Кроме того, при повторном обновлении сеть в конечном итоге сойдется к состоянию, которое является местный минимум в энергетической функции^{[нужна цитата ]} (который считается Функция Ляпунова ). Таким образом, если состояние является локальным минимумом функции энергии, это стабильное состояние для сети. Отметим, что эта функция энергии принадлежит к общему классу моделей в физика под именем Модели Изинга; это, в свою очередь, частный случай Марковские сети, поскольку связанный вероятностная мера, то Мера Гиббса, имеет Марковская собственность.

Сеть Хопфилда в оптимизации

Хопфилд и Танк представили сетевое приложение Хопфилда для решения классической задачи коммивояжера в 1985 году.^[9] С тех пор сеть Хопфилда широко использовалась для оптимизации. Идея использования сети Хопфилда в задачах оптимизации проста: если ограниченная / неограниченная функция затрат может быть записана в форме энергетической функции Хопфилда E, то существует сеть Хопфилда, точки равновесия которой представляют решения для оптимизации с ограничениями / без ограничений. проблема. Минимизация функции энергии Хопфилда минимизирует целевую функцию и удовлетворяет ограничениям, так как ограничения «встраиваются» в синаптические веса сети. Хотя включение оптимизационных ограничений в синаптические веса наилучшим образом является сложной задачей, на самом деле многие различные сложные задачи оптимизации с ограничениями в различных дисциплинах были преобразованы в функцию энергии Хопфилда: системы ассоциативной памяти, аналого-цифровое преобразование, проблема планирования рабочего места, квадратичное назначение и другие связанные с ней NP-завершенные задачи, проблема распределения каналов в беспроводных сетях, проблема маршрутизации в мобильной сети ad-hoc, восстановление изображения, идентификация системы, комбинаторная оптимизация и т. д., и это лишь некоторые из них. Более подробную информацию можно найти, например, в бумага.^[7]  

Инициализация и запуск

Инициализация сетей Хопфилда выполняется путем установки значений единиц на желаемый стартовый образец. Затем выполняются повторные обновления до тех пор, пока сеть не сходится к шаблону аттрактора. Сходимость обычно гарантирована, поскольку Хопфилд доказал, что аттракторы этого нелинейная динамическая система стабильны, а не периодичны или хаотичны, как в некоторых других системах^{[нужна цитата ]}. Следовательно, в контексте сетей Хопфилда шаблон аттрактора - это конечное стабильное состояние, шаблон, который не может изменить какое-либо значение в нем при обновлении.^{[нужна цитата ]}.

Обучение персонала

Обучение сети Хопфилда включает в себя снижение энергии состояний, которые сеть должна «запоминать». Это позволяет сети служить системой памяти с адресацией по содержанию, то есть сеть будет сходиться к «запомненному» состоянию, если ей дана только часть состояния. Сеть может использоваться для восстановления после искаженного ввода до обученного состояния, которое наиболее похоже на этот ввод. Это называется ассоциативной памятью, потому что она восстанавливает воспоминания на основе сходства. Например, если мы обучаем сеть Хопфилда с пятью единицами, так что состояние (1, -1, 1, -1, 1) является минимумом энергии, и мы даем сети состояние (1, -1, -1, -1, 1) он сходится к (1, -1, 1, -1, 1). Таким образом, сеть правильно обучается, когда энергия состояний, которую она должна запомнить, является локальным минимумом. Обратите внимание, что в отличие от Перцептрон при обучении пороги нейронов никогда не обновляются.

Правила обучения

Есть разные разные правила обучения которые можно использовать для хранения информации в памяти сети Хопфилда. Желательно, чтобы обучающее правило обладало обоими из следующих двух свойств:

• Местный: Правило обучения местный если каждый вес обновляется с использованием информации, доступной нейронам по обе стороны от соединения, которое связано с этим конкретным весом.
• Инкрементальный: Новые шаблоны можно изучать без использования информации из старых шаблонов, которые также использовались для обучения. То есть, когда для обучения используется новый шаблон, новые значения весов зависят только от старых значений и от нового шаблона.^[10]

Эти свойства желательны, поскольку удовлетворяющее им правило обучения более правдоподобно с биологической точки зрения. Например, поскольку человеческий мозг постоянно изучает новые концепции, можно предположить, что человеческое обучение идет постепенно. Система обучения, которая не была инкрементальной, обычно обучалась только один раз с огромным пакетом обучающих данных.

Правило обучения Hebbian для сетей Хопфилда

В Hebbian Theory был введен Дональдом Хеббом в 1949 году для объяснения «ассоциативного обучения», при котором одновременная активация нейронных клеток приводит к выраженному увеличению синаптической силы между этими клетками.^[11] Это часто резюмируется как «Нейроны, которые срабатывают вместе, соединяются вместе. Нейроны, которые срабатывают не синхронно, не могут связываться».

Правило Hebbian является одновременно локальным и инкрементальным. Для сетей Хопфилда это реализуется следующим образом при обучении ${\displaystyle n}$бинарные шаблоны:

${\displaystyle w_{ij}={\frac {1}{n}}\sum _{\mu =1}^{n}\epsilon _{i}^{\mu }\epsilon _{j}^{\mu }}$

куда ${\displaystyle \epsilon _{i}^{\mu }}$ представляет бит i из шаблона ${\displaystyle \mu }$.

Если биты, соответствующие нейронам i и j, равны по шаблону ${\displaystyle \mu }$, то продукт ${\displaystyle \epsilon _{i}^{\mu }\epsilon _{j}^{\mu }}$ будет положительным. Это, в свою очередь, положительно скажется на весе. ${\displaystyle w_{ij}}$ и значения i и j будут стремиться стать равными. Обратное происходит, если биты, соответствующие нейронам i и j, различны.

Правило обучения аиста

Это правило было введено Амос Сторки в 1997 году и носит как локальный, так и постепенный характер. Сторки также показал, что сеть Хопфилда, обученная с использованием этого правила, имеет большую пропускную способность, чем соответствующая сеть, обученная с использованием правила Хеббиана.^[12] Матрица весов аттракторной нейронной сети^{[требуется разъяснение ]} Говорят, что он следует правилу обучения аиста, если подчиняется:

${\displaystyle w_{ij}^{\nu }=w_{ij}^{\nu -1}+{\frac {1}{n}}\epsilon _{i}^{\nu }\epsilon _{j}^{\nu }-{\frac {1}{n}}\epsilon _{i}^{\nu }h_{ji}^{\nu }-{\frac {1}{n}}\epsilon _{j}^{\nu }h_{ij}^{\nu }}$

куда ${\displaystyle h_{ij}^{\nu }=\sum _{k=1~:~i\neq k\neq j}^{n}w_{ik}^{\nu -1}\epsilon _{k}^{\nu }}$ это форма местное поле ^[10] на нейроне i.

Это правило обучения является локальным, поскольку синапсы учитывают только нейроны по бокам. Правило использует больше информации из шаблонов и весов, чем обобщенное правило Хебба, из-за эффекта локального поля.

Ложные узоры

Шаблоны, которые сеть использует для обучения (называемые состояния поиска) становятся аттракторами системы. Повторные обновления в конечном итоге приведут к сходимости к одному из состояний поиска. Однако иногда сеть сходится к ложным шаблонам (отличным от шаблонов обучения).^[13] Энергия в этих ложных паттернах также является локальным минимумом. Для каждого сохраненного шаблона x отрицание -x также является ложным шаблоном.

Ложное состояние также может быть линейная комбинация нечетного числа состояний поиска. Например, при использовании 3 узоров ${\displaystyle \mu _{1},\mu _{2},\mu _{3}}$, можно получить следующее ложное состояние:

${\displaystyle \epsilon _{i}^{\rm {mix}}=\pm \operatorname {sgn}(\pm \epsilon _{i}^{\mu _{1}}\pm \epsilon _{i}^{\mu _{2}}\pm \epsilon _{i}^{\mu _{3}})}$

Ложные паттерны с четным числом состояний не могут существовать, так как они могут давать в сумме ноль. ^[13]

Емкость

Пропускная способность сети в сетевой модели Хопфилда определяется количеством нейронов и связями в данной сети. Следовательно, количество воспоминаний, которые можно сохранить, зависит от нейронов и связей. Кроме того, было показано, что точность отзыва между векторами и узлами составляла 0,138 (примерно 138 векторов можно вызвать из хранилища на каждые 1000 узлов) (Hertz et al., 1991). Таким образом, очевидно, что при попытке сохранить большое количество векторов произойдет много ошибок. Когда модель Хопфилда не запоминает правильный шаблон, возможно, что произошло вторжение, поскольку семантически связанные элементы имеют тенденцию вводить в заблуждение человека, и происходит вспоминание неправильного шаблона. Таким образом, сетевая модель Хопфилда при извлечении путает один сохраненный элемент с другим. Идеальные отзывы и высокая емкость,> 0,14, могут быть загружены в сеть с помощью метода обучения Storkey; ETAM,^[14][15] ETAM также экспериментирует в.^[16] Позднее были разработаны дополнительные модели, вдохновленные сетью Хопфилда, чтобы увеличить лимит памяти и снизить частоту ошибок при извлечении, при этом некоторые из них были способны однократное обучение.^[17]

Емкость хранилища может быть задана как ${\displaystyle C\cong {\frac {n}{2\log _{2}n}}}$ куда ${\displaystyle n}$ - количество нейронов в сети. Или примерно ${\displaystyle C\approxeq 0.15n}$^[18]

Человеческая память

Модель Хопфилда учитывает ассоциативный объем памяти за счет включения векторов памяти. Векторы памяти можно использовать немного, и это вызовет поиск наиболее похожего вектора в сети. Однако мы выясним, что из-за этого процесса могут происходить вторжения. В ассоциативной памяти для сети Хопфилда есть два типа операций: автоассоциация и гетероассоциация. Первый - когда вектор связан сам с собой, а второй - когда два разных вектора связаны в хранилище. Кроме того, оба типа операций можно хранить в одной матрице памяти, но только если данная матрица представления не является одной или другой из операций, а скорее является их комбинацией (автоассоциативной и гетероассоциативной). Важно отметить, что сетевая модель Хопфилда использует то же правило обучения, что и Правило обучения Хебба (1949), который в основном пытался показать, что обучение происходит в результате усиления весов во время активности.

Риццуто и Кахана (2001) смогли показать, что модель нейронной сети может учитывать повторение при точности отзыва путем включения алгоритма вероятностного обучения. В процессе поиска не происходит обучения. В результате веса сети остаются фиксированными, показывая, что модель может переключаться с этапа обучения на этап отзыва. Добавляя контекстуальный дрейф, они смогли показать быстрое забывание, которое происходит в модели Хопфилда во время задания на вызов. Вся сеть способствует изменению активации любого отдельного узла.

Динамическое правило Маккаллоха и Питтса (McCulloch and Pitts, 1943), описывающее поведение нейронов, делает это таким образом, чтобы показать, как активация нескольких нейронов отображается на активацию скорости возбуждения нового нейрона и как веса нейронов усиливают синаптические связи между новым активированным нейроном (и теми, которые его активировали). Хопфилд использовал динамическое правило Маккаллоха – Питтса, чтобы показать, как поиск возможен в сети Хопфилда. Однако важно отметить, что Хопфилд делал это неоднократно. Хопфилд будет использовать нелинейную функцию активации вместо использования линейной функции. Таким образом, это создаст динамическое правило Хопфилда, и с его помощью Хопфилд смог показать, что с помощью нелинейной функции активации динамическое правило всегда будет изменять значения вектора состояния в направлении одного из сохраненных шаблонов.

Смотрите также

• Ассоциативная память (значения)
• Автоассоциативная память
• Машина Больцмана - как сеть Хопфилда, но использует отожженную выборку Гиббса вместо градиентного спуска
• Модель динамических систем познания
• Модель Изинга
• Хеббийская теория

Рекомендации

1. Герни, Кевин (2002). Введение в нейронные сети. Рутледж. ISBN  978-1857285031.
2. Сатхасивам, Саратха (2008). «Логическое обучение в сетях Хопфилда». arXiv:0804.4075 [cs.LO ].
3. Амит, Дэниел Дж. Моделирование функции мозга: мир нейронных сетей аттрактора. Издательство Кембриджского университета, 1992 г.
4. Роллс, Эдмунд Т. Кора головного мозга: принципы работы. Oxford University Press, 2016 г.
5. Маккей, Дэвид Дж. С. (2003). «42. Hopfield Networks». Теория информации, логические выводы и алгоритмы обучения. Издательство Кембриджского университета. п.508. ISBN  978-0521642989. Это доказательство сходимости во многом зависит от того факта, что связи сети Хопфилда симметричный. Это также зависит от асинхронных обновлений.
6. Дж. Брук, “О свойствах сходимости модели Хопфилда”, Тр. IEEE, т. 78, pp. 1579–1585, октябрь 1990 г.
7. З. Уйкан. «О принципах работы нейронных сетей Хопфилда и их эквивалентности GADIA в оптимизации», IEEE Transactions on Neural Networks and Learning Systems, стр. 1-11, 2019 г. (DOI: 10.1109 / TNNLS.2019.2940920) (связь)
8. З. Уйкан, «Shadow-Cuts Minimization / Maximization and Complex Hopfield Neural Networks», IEEE Transactions on Neural Networks and Learning Systems, pp.1-11, 2020. (DOI: 10.1109 / TNNLS.2020.2980237). (Открытый доступ)
9. J.J. Хопфилд и Д. Танк. «Нейронное вычисление решений в задачах оптимизации». Биологическая кибернетика 55, стр: 141-146, (1985).
10. Сторки, Амос Дж. И Ромен Валабрег. «Источники притяжения нового правила обучения Хопфилда». Нейронные сети 12.6 (1999): 869-876.
11. Хебб, Дональд Олдинг. Организация поведения: нейропсихологическая теория. Лоуренс Эрлбаум, 2002.
12. Сторки, Амос. «Увеличение емкости сети Хопфилда без ущерба для функциональности». Искусственные нейронные сети - ICANN'97 (1997 г.): 451-456.
13. Герц, Джон А., Андерс С. Крог и Ричард Г. Палмер. Введение в теорию нейронных вычислений. Vol. 1. Вествью пресс, 1991.
14. Liou, C.-Y .; Линь, С.-Л. (2006). «Конечная загрузка памяти в волосатых нейронах». Естественные вычисления. 5 (1): 15–42. Дои:10.1007 / s11047-004-5490-х. S2CID  35025761.
15. Liou, C.-Y .; Юань, С.-К. (1999). «Устойчивая к ошибкам ассоциативная память». Биологическая кибернетика. 81 (4): 331–342. Дои:10.1007 / s004220050566. PMID  10541936. S2CID  6168346.
16. Юань, С.-К. (Июнь 1997 г.). Расширение бассейнов притяжения ассоциативной памяти (Магистерская диссертация). Национальный Тайваньский университет. 991010725609704786.
17. АБУДИБ, штат Алабама; ГРИПОН, Винсент; ЦЗЯН, Сяорань (2014). «Исследование алгоритмов поиска разреженных сообщений в сетях нейронных клик». КОГНИТИВ 2014: 6-я Международная конференция по передовым когнитивным технологиям и приложениям: 140–146. arXiv:1308.4506. Bibcode:2013arXiv1308.4506A.
18. Раджашекаран, Сундарамурти. (2003). Нейронные сети, нечеткая логика и генетические алгоритмы: синтез и приложения. Пай, Г. А. Виджаялакшми. (Восточная экономика ред.). Нью-Дели: Прентис-Холл Индии. ISBN  81-203-2186-3. OCLC  56960832.

• Дж. Дж. Хопфилд, «Нейронные сети и физические системы с возникающими коллективными вычислительными возможностями», Труды Национальной академии наук США, т. 79 нет. 8 с. 2554–2558, апрель 1982 г.
• Хебб, Д.О. (1949). Организация поведения. Нью-Йорк: Уайли
• Герц, Дж., Крог, А., и Палмер, Р. (1991). Введение в теорию нейронных вычислений. Редвуд-Сити, Калифорния: Эддисон-Уэсли.
• McCulloch, W.S .; Питтс, W.H. (1943). «Логический исчисление идей, присущих нервной деятельности». Бюллетень математической биофизики. 5 (4): 115–133. Дои:10.1007 / BF02478259.
• Polyn, S.M .; Кахана, М.Дж. (2008). «Поиск в памяти и нейронное представление контекста». Тенденции в когнитивных науках. 12 (1): 24–30. Дои:10.1016 / j.tics.2007.10.010. ЧВК  2839453. PMID  18069046.
• Rizzuto, D.S .; Кахана, М.Дж. (2001). «Автоассоциативная модель нейронной сети парно-ассоциативного обучения». Нейронные вычисления. 13 (9): 2075–2092. CiteSeerX  10.1.1.45.7929. Дои:10.1162/089976601750399317. PMID  11516358. S2CID  7675117.
• Kruse, Borgelt, Klawonn, Moewes, Russ, Steinbrecher (2011). Вычислительный интеллект.

внешняя ссылка

• Глава 13 Модель Хопфилда из Нейронные сети - систематическое введение от Рауля Рохаса (ISBN  978-3-540-60505-8)
• Javascript сети Хопфилда
• Задача коммивояжера - JAVA-апплет нейронной сети Хопфилда
• scholarpedia.org - сеть Хопфилда - Статья Джона Хопфилда о сетях Хопфилда
• Обучение сети Хопфилда с использованием детерминированных скрытых переменных - Учебник Тристана Флетчера
• Графический интерфейс Neural Lab - Графический интерфейс нейронной сети Хопфилда (Python & gtk)