Логическая сеть - Boolean network
Эта статья может требовать уборка встретиться с Википедией стандарты качества. (Август 2011 г.) (Узнайте, как и когда удалить этот шаблон сообщения) |
| Сетевая наука | ||||
|---|---|---|---|---|
| Типы сетей | ||||
| Графики | ||||
| ||||
| Модели | ||||
| ||||
| ||||
| ||||
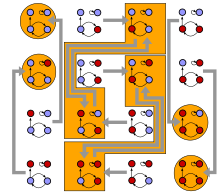
А Логическая сеть состоит из дискретного набора логические переменные каждый из которых имеет Логическая функция (возможно, разный для каждой переменной), назначенный ему, который принимает входные данные из подмножества этих переменных и выход, который определяет состояние переменной, которой он назначен. Фактически этот набор функций определяет топологию (связность) для набора переменных, которые затем становятся узлами в сеть. Обычно динамику системы принимают за дискретную Временные ряды где состояние всей сети в момент времени т+1 определяется путем оценки функции каждой переменной в состоянии сети в момент времени. т. Это может быть сделано синхронно или же асинхронно.[1]
Булевы сети использовались в биологии для моделирования регуляторных сетей. Хотя логические сети являются грубым упрощением генетической реальности, где гены не являются простыми бинарными переключателями, есть несколько случаев, когда они правильно фиксируют правильный паттерн экспрессируемых и подавленных генов.[2][3] На первый взгляд математически простая (синхронная) модель была полностью понята только в середине 2000-х годов.[4]
Классическая модель
Логическая сеть - это особый вид последовательная динамическая система, где время и состояния дискретны, т.е. как набор переменных, так и набор состояний во временном ряду имеют биекция на целочисленный ряд. Такие системы похожи на клеточные автоматы в сетях, за исключением того факта, что при их настройке каждый узел имеет правило, которое выбирается случайным образом из всех 22K возможные с K входы. С К = 2 поведение класса 2 имеет тенденцию к преобладанию. Но для К> 2, наблюдаемое поведение быстро приближается к типичному для случайного отображения, в котором сеть, представляющая эволюцию 2N государства N базовые узлы сами по себе связаны по существу случайным образом.[5]
А случайная логическая сеть (RBN) - это сеть, которая выбирается случайным образом из набора всех возможных логических сетей определенного размера, N. Затем можно статистически изучить, как ожидаемые свойства таких сетей зависят от различных статистических свойств ансамбля всех возможных сетей. Например, можно изучить, как поведение RBN изменяется при изменении средней возможности подключения.
Первые булевы сети были предложены Стюарт А. Кауфман в 1969 г., как случайный модели генетические регуляторные сети[6] но их математическое понимание началось только в 2000-х годах.[7][8]
Аттракторы
Поскольку в булевой сети всего 2N возможных состояний, траектория рано или поздно достигнет ранее посещенного состояния, и, таким образом, поскольку динамика детерминирована, траектория перейдет в устойчивое состояние или цикл, называемый аттрактор (хотя в более широком поле динамических систем цикл является аттрактором только в том случае, если возмущения от него приводят к нему). Если аттрактор имеет только одно состояние, он называется точечный аттрактор, и если аттрактор состоит из более чем одного состояния, он называется аттрактор цикла. Множество состояний, приводящих к аттрактору, называется бассейн аттрактора. Состояния, которые возникают только в начале траекторий (траектории не ведут к их), называются Эдемский сад состояния[9] и динамика сетевого потока из этих состояний к аттракторам. Время, необходимое для достижения аттрактора, называется переходное время.[4]
С ростом мощности компьютеров и растущим пониманием, казалось бы, простой модели, разные авторы дали разные оценки среднего числа и длины аттракторов, здесь краткое изложение ключевых публикаций.[10]
| Автор | Год | Средняя длина аттрактора | Среднее число аттрактора | комментарий |
|---|---|---|---|---|
| Кауфманн [6] | 1969 | |||
| Бастолла / Паризи[11] | 1998 | быстрее степенного закона, | быстрее степенного закона, | первые числовые свидетельства |
| Бильке / Сюннессон[12] | 2002 | линейно с размером системы, | ||
| Socolar / Kauffman[13] | 2003 | быстрее линейного, с | ||
| Самуэльссон / Троен[14] | 2003 | суперполиномиальный рост, | математическое доказательство | |
| Михальев / Дроссель[15] | 2005 | быстрее степенного закона, | быстрее степенного закона, |
Стабильность
В теории динамических систем структура и длина аттракторов сети соответствуют динамической фазе сети. В устойчивость булевых сетей зависит от связей их узлы. Логическая сеть может показывать стабильную, критическую или хаотичное поведение. Это явление регулируется критическим значением среднего числа соединений узлов () и может характеризоваться Расстояние Хэмминга как мера расстояния. В нестабильном режиме расстояние между двумя изначально близкими состояниями в среднем увеличивается во времени по экспоненте, а в устойчивом - по экспоненте. В этом случае под «изначально близкими состояниями» подразумевается, что расстояние Хэмминга мало по сравнению с количеством узлов () в сети.
За N-K-модель[16] сеть стабильна, если , критично, если , и нестабильно, если .
Состояние данного узла обновляется в соответствии с его таблица истинности, выходы которого заполняются случайным образом. обозначает вероятность присвоения выключенного выхода данной серии входных сигналов.
Если для каждого узла переход между стабильным и хаотическим диапазоном зависит от . В соответствии с Бернард Деррида и Ив Помо[17], критическое значение среднего числа подключений равно .
Если не является постоянным, и нет корреляции между входными и выходными градусами, условия устойчивости определяются [18][19][20] Сеть стабильна, если , критично, если , и нестабильно, если .
Условия устойчивости такие же в случае сетей с безмасштабный топология где внутреннее и внешнее распределение является степенным распределением: , и , поскольку каждая исходящая ссылка от узла является входящей ссылкой на другую.[21]
Чувствительность показывает вероятность того, что выход логической функции данного узла изменится, если его вход изменится. Для случайных булевых сетей. В общем случае стабильность сети определяется наибольшим собственное значение матрицы , куда , и это матрица смежности сети.[22] Сеть стабильна, если , критично, если , нестабильно, если .
Вариации модели
Другие топологии
Одна тема - учиться другой базовый топологии графов.
- Однородный случай просто относится к сетке, которая является простой редукцией к известному Модель Изинга.
- Без накипи топологии могут быть выбраны для булевых сетей.[23] Можно выделить случай, когда только степенное распределение по степенному закону,[24] либо только распределение исходящих степеней, либо и то, и другое.
Другие схемы обновления
Классические логические сети (иногда называемые CRBN, т.е. классическая случайная логическая сеть) обновляются синхронно. Мотивировавшись тем, что гены обычно не меняют свое состояние одновременно,[25] были представлены различные альтернативы. Общая классификация[26] следующее:
- Детерминированные асинхронные обновленные логические сети (DRBNs) не обновляются синхронно, но детерминированное решение все еще существует. Узел я будет обновлено, когда т ≡ Qя (мод пя) куда т это временной шаг.[27]
- Самый общий случай - полное стохастическое обновление (ГАРБН, общие асинхронные случайные логические сети). Здесь один (или несколько) узлов выбирается на каждом этапе вычислений для обновления.
- В Частично наблюдаемая логическая динамическая система (POBDS)[28][29][30][31] Модель сигнала отличается от всех предыдущих детерминированных и стохастических булевых сетевых моделей тем, что устраняет предположение о прямой наблюдаемости вектора логического состояния и допускает неопределенность в процессе наблюдения, обращаясь к сценарию, встречающемуся на практике.
Применение логических сетей
Классификация
- В Масштабируемая оптимальная байесовская классификация[32] разработал оптимальную классификацию траекторий с учетом потенциальной неопределенности модели, а также предложил классификацию траекторий на основе частиц, которая хорошо масштабируется для больших сетей с гораздо меньшей сложностью, чем оптимальное решение.
Смотрите также
Рекомендации
- ^ Naldi, A .; Monteiro, P.T .; Mussel, C .; Kestler, H.A .; Thieffry, D .; Xenarios, I .; Saez-Rodriguez, J .; Геликар, Т .; Чауйя, К. (25 января 2015 г.). «Совместная разработка стандартов и инструментов логического моделирования с CoLoMoTo». Биоинформатика. 31 (7): 1154–1159. Дои:10.1093 / биоинформатика / btv013. PMID 25619997.
- ^ Альберт, Река; Отмер, Ханс Дж. (Июль 2003 г.). «Топология регуляторных взаимодействий предсказывает паттерн экспрессии генов полярности сегментов у Drosophila melanogaster». Журнал теоретической биологии. 223 (1): 1–18. CiteSeerX 10.1.1.13.3370. Дои:10.1016 / S0022-5193 (03) 00035-3. ЧВК 6388622. PMID 12782112.
- ^ Li, J .; Bench, A.J .; Василиу, Г. С .; Fourouclas, N .; Ferguson-Smith, A.C .; Грин, А. Р. (30 апреля 2004 г.). «Импринтинг человеческого гена L3MBTL, члена семейства поликомб, локализованного в области хромосомы 20, удаленной в миелоидных злокачественных новообразованиях человека». Труды Национальной академии наук. 101 (19): 7341–7346. Bibcode:2004ПНАС..101.7341Л. Дои:10.1073 / pnas.0308195101. ЧВК 409920. PMID 15123827.
- ^ а б Дроссель, Барбара (декабрь 2009 г.). «Случайные булевы сети». В Шустере, Хайнц Георг (ред.). Глава 3. Случайные булевы сети. Обзоры нелинейной динамики и сложности. Вайли. С. 69–110. arXiv:0706.3351. Дои:10.1002 / 9783527626359.ch3. ISBN 9783527626359. S2CID 119300231.
- ^ Вольфрам, Стивен (2002). Новый вид науки. Шампейн, Иллинойс: Wolfram Media, Inc., стр.936. ISBN 978-1579550080. Получено 15 марта 2018.
- ^ а б Кауфман, Стюарт (11 октября 1969). «Гомеостаз и дифференциация в случайных генетических сетях контроля». Природа. 224 (5215): 177–178. Bibcode:1969Натура.224..177K. Дои:10.1038 / 224177a0. PMID 5343519. S2CID 4179318.
- ^ Алдана, Максимо; Медник, Сьюзен; Каданов, Лео П. (2003). Булева динамика со случайными связями. Перспективы и проблемы нелинейных наук. С. 23–89. arXiv:nlin / 0204062. Дои:10.1007/978-0-387-21789-5_2. ISBN 978-1-4684-9566-9. S2CID 15024306.
- ^ Гершенсон, Карлос (2004). «Введение в случайные булевы сети». В Беду, М., П. Хазбандс, Т. Хаттон, С. Кумар и Х. Судзуки (редакторы). Практикум и учебные материалы, Девятая Международная конференция по моделированию и синтезу живых систем (ALife IX). Пп. 2004: 160–173. arXiv:nlin.AO/0408006. Bibcode:2004nlin ...... 8006G.
- ^ Вуэнше, Эндрю (2011). Изучение дискретной динамики: [руководство DDLab: инструменты для исследования клеточных автоматов, случайных логических и многозначных Neworks [sic] и не только]. Фроум, Англия: Luniver Press. п. 16. ISBN 9781905986316. Получено 12 января 2016.
- ^ Грейл, Флориан (2012). «Булевы сети как каркас моделирования». Границы науки о растениях. 3: 178. Дои:10.3389 / fpls.2012.00178. ЧВК 3419389. PMID 22912642.
- ^ Bastolla, U .; Паризи, Г. (май 1998 г.). «Модульная структура сетей Кауфмана». Physica D: нелинейные явления. 115 (3–4): 219–233. arXiv:cond-mat / 9708214. Bibcode:1998PhyD..115..219B. Дои:10.1016 / S0167-2789 (97) 00242-X. S2CID 1585753.
- ^ Бильке, Свен; Сюннессон, Фредрик (декабрь 2001 г.). «Устойчивость модели Кауфмана». Физический обзор E. 65 (1): 016129. arXiv:cond-mat / 0107035. Bibcode:2002PhRvE..65a6129B. Дои:10.1103 / PhysRevE.65.016129. PMID 11800758. S2CID 2470586.
- ^ Socolar, J .; Кауфман, С. (февраль 2003 г.). «Масштабирование в упорядоченных и критических случайных булевых сетях». Письма с физическими проверками. 90 (6): 068702. arXiv:cond-mat / 0212306. Bibcode:2003ПхРвЛ..90ф8702С. Дои:10.1103 / PhysRevLett.90.068702. PMID 12633339. S2CID 14392074.
- ^ Самуэльссон, Бьорн; Троен, Карл (март 2003 г.). «Суперполиномиальный рост числа аттракторов в сетях Кауфмана». Письма с физическими проверками. 90 (9): 098701. Bibcode:2003ПхРвЛ..90и8701С. Дои:10.1103 / PhysRevLett.90.098701. PMID 12689263.
- ^ Михальев, Тамара; Дроссель, Барбара (октябрь 2006 г.). «Масштабирование в общем классе критических случайных булевых сетей». Физический обзор E. 74 (4): 046101. arXiv:cond-mat / 0606612. Bibcode:2006ПхРвЭ..74д6101М. Дои:10.1103 / PhysRevE.74.046101. PMID 17155127. S2CID 17739744.
- ^ Кауфман, С. А. (1969). «Метаболическая стабильность и эпигенез в случайно построенных генетических сетях». Журнал теоретической биологии. 22 (3): 437–467. Дои:10.1016/0022-5193(69)90015-0. PMID 5803332.
- ^ Деррида, B; Помо, Y (1986-01-15). "Случайные сети автоматов: простое отожженное приближение". Письма Europhysics (EPL). 1 (2): 45–49. Bibcode:1986EL ...... 1 ... 45D. Дои:10.1209/0295-5075/1/2/001.
- ^ Solé, Ricard V .; Луке, Бартоло (1995-01-02). «Фазовые переходы и антихаос в обобщенных сетях Кауфмана». Письма о физике A. 196 (5–6): 331–334. Bibcode:1995ФЛА..196..331С. Дои:10.1016 / 0375-9601 (94) 00876-Q.
- ^ Луке, Бартоло; Соле, Рикар В. (1997-01-01). «Фазовые переходы в случайных сетях: простое аналитическое определение критических точек». Физический обзор E. 55 (1): 257–260. Bibcode:1997PhRvE..55..257L. Дои:10.1103 / PhysRevE.55.257.
- ^ Фокс, Джеффри Дж .; Хилл, Колин С. (2001-12-01). «От топологии к динамике в биохимических сетях». Хаос: междисциплинарный журнал нелинейной науки. 11 (4): 809–815. Bibcode:2001 Хаос..11..809F. Дои:10.1063/1.1414882. ISSN 1054-1500. PMID 12779520.
- ^ Алдана, Максимино; Клюзель, Филипп (22 июля 2003 г.). «Естественный класс надежных сетей». Труды Национальной академии наук. 100 (15): 8710–8714. Bibcode:2003ПНАС..100.8710А. Дои:10.1073 / pnas.1536783100. ISSN 0027-8424. ЧВК 166377. PMID 12853565.
- ^ Померанс, Эндрю; Отт, Эдвард; Гирван, Мишель; Лозерт, Вольфганг (19 мая 2009 г.). «Влияние топологии сети на устойчивость моделей дискретного состояния генетического контроля». Труды Национальной академии наук. 106 (20): 8209–8214. arXiv:0901.4362. Bibcode:2009ПНАС..106.8209П. Дои:10.1073 / pnas.0900142106. ISSN 0027-8424. ЧВК 2688895. PMID 19416903.
- ^ Алдана, Максимино (октябрь 2003 г.). «Булева динамика сетей с безмасштабной топологией». Physica D: нелинейные явления. 185 (1): 45–66. arXiv:cond-mat / 0209571. Bibcode:2003Фид..185 ... 45А. Дои:10.1016 / с0167-2789 (03) 00174-х.
- ^ Дроссель, Барбара; Грейл, Флориан (4 августа 2009 г.). «Критические булевы сети с безмасштабным распределением по степеням». Физический обзор E. 80 (2): 026102. arXiv:0901.0387. Bibcode:2009PhRvE..80b6102D. Дои:10.1103 / PhysRevE.80.026102. PMID 19792195. S2CID 2487442.
- ^ Харви, Имман; Босомайер, Терри (1997). Мужья, Фил; Харви, Имман (ред.). Время вне стыка: аттракторы в асинхронных случайных булевых сетях. Труды Четвертой Европейской конференции по искусственной жизни (ECAL97). MIT Press. С. 67–75. ISBN 9780262581578.
- ^ Гершенсон, Карлос (2002). Стэндиш, Рассел К.; Бедо, Марк А (ред.). Классификация случайных булевых сетей. Материалы восьмой Международной конференции по искусственной жизни. Искусственная жизнь. 8. Кембридж, Массачусетс, США. С. 1–8. arXiv:cs / 0208001. Bibcode:2002cs ........ 8001G. ISBN 9780262692816. Получено 12 января 2016.
- ^ Гершенсон, Карлос; Брокерт, Ян; Аэртс, Дидерик (14 сентября 2003 г.). Контекстные случайные булевы сети [7-я Европейская конференция, ECAL 2003]. Успехи в искусственной жизни. Конспект лекций по информатике. 2801. Дортмунд, Германия. С. 615–624. arXiv:nlin / 0303021. Дои:10.1007/978-3-540-39432-7_66. ISBN 978-3-540-39432-7. S2CID 4309400.
- ^ Imani, M .; Брага-Нето, У. М. (01.01.2017). "Адаптивный фильтр максимального правдоподобия для частично наблюдаемых булевых динамических систем". Транзакции IEEE при обработке сигналов. 65 (2): 359–371. arXiv:1702.07269. Bibcode:2017ITSP ... 65..359I. Дои:10.1109 / TSP.2016.2614798. ISSN 1053-587X. S2CID 178376.
- ^ Imani, M .; Брага-Нето, У. М. (2015). «Оценка оптимального состояния для булевых динамических систем с использованием булевого сглаживания Калмана». 2015 Глобальная конференция IEEE по обработке сигналов и информации (GlobalSIP). С. 972–976. Дои:10.1109 / GlobalSIP.2015.7418342. ISBN 978-1-4799-7591-4. S2CID 8672734.
- ^ Imani, M .; Брага-Нето, У. М. (2016). Американская конференция по контролю за 2016 г. (ACC). С. 227–232. Дои:10.1109 / ACC.2016.7524920. ISBN 978-1-4673-8682-1. S2CID 7210088.
- ^ Imani, M .; Брага-Нето, У. (01.12.2016). Итерация по точкам для частично наблюдаемых булевых динамических систем с конечным пространством наблюдения. 55-я конференция IEEE по вопросам принятия решений и контроля (CDC), 2016 г.. С. 4208–4213. Дои:10.1109 / CDC.2016.7798908. ISBN 978-1-5090-1837-6. S2CID 11341805.
- ^ Хаджирамезанали, Э., Имани, М., Брага-Нето, У. и Циан, X., Догерти, Э .. Масштабируемая оптимальная байесовская классификация траекторий отдельных клеток в условиях неопределенности регулирующей модели. ACMBCB'18. https://dl.acm.org/citation.cfm?id=3233689
- Дуброва Е., Тесленко М., Мартинелли А. (2005). *Сети Кауфмана: анализ и приложения, в "Proceedings of International Conference on Computer Aided Design", pages 479-484.
внешняя ссылка
- DDLab
- Анализ динамических алгебраических моделей (ADAM) v1.1
- RBNLab
- Симулятор логических сетей NetBuilder
- Симулятор логической сети с открытым исходным кодом
- Сеть Кауфмана JavaScript
- Вероятностные булевы сети (PBN)
- Инструмент на основе SAT для вычисления аттракторов в булевых сетях
- CoLoMoTo (Консорциум логических моделей и инструментов)


















![{displaystyle K_ {c} = 1 / [2p (1-p)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c2bd3f5ed2909d2e20e8641b9788d1ba3fca171d)














