Контактный процесс (математика) - Contact process (mathematics)
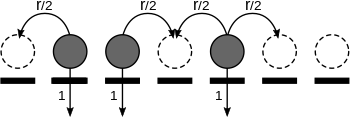
В контактный процесс это случайный процесс используется для моделирования роста населения на множестве сайтов из график в которых занятые участки становятся вакантными с постоянной скоростью, а свободные участки становятся занятыми со скоростью, пропорциональной количеству занятых соседних участков. Следовательно, если обозначить через константа пропорциональности, каждый сайт остается занятым в течение случайного периода времени, который экспоненциально распределенный параметр 1 и помещает потомков на каждое свободное соседнее место во время событий Пуассоновский процесс параметр в течение этого периода. Все процессы независимый друг друга и случайный период времени сайты остаются занятыми. Процесс контакта также можно интерпретировать как модель распространения инфекции, рассматривая частицы как бактерии, распространяющиеся по людям, расположенным в местах заражения. занятые участки соответствуют инфицированным лицам, а свободные - здоровым.
Основная интересная величина - это количество частиц в процессе, например , в первой интерпретации, что соответствует количеству зараженных сайтов во второй. Следовательно, процесс выживает всякий раз, когда число частиц всегда положительное, что соответствует случаю, когда во втором случае всегда есть инфицированные люди. Для любого бесконечного графа существует положительное и конечное критическое значение так что если то выживание процесса, начиная с конечного числа частиц, происходит с положительной вероятностью, а если их исчезновение почти наверняка. Обратите внимание, что сокращение до абсурда и теорема о бесконечной обезьяне, выживаемость процесса эквивалентна , в качестве , тогда как вымирание эквивалентно , в качестве , и поэтому естественно спросить, с какой скоростью когда процесс выживает.
Математическое определение
Если состояние процесса во время является , затем сайт в занята, скажем, частицей, если и вакантно, если . Контактный процесс длится непрерывно. Марковский процесс с пространством состояний , куда является конечным или счетным график, обычно , и частный случай система взаимодействующих частиц В частности, динамика основного процесса контакта определяется следующими темпами перехода: на месте ,
где сумма по всем соседям из в . Это означает, что каждый сайт ожидает экспоненциальное время с соответствующей скоростью, а затем переворачивается (так что 0 становится 1 и наоборот).
Подключение к Перколяция
Контактный процесс - это случайный процесс это тесно связано с теория перколяции. Тед Харрис (1974) отметили, что контактный процесс на ℤd когда инфекции и выздоровление могут происходить только в дискретное время соответствует пошаговой перколяции связей на графе, полученном путем ориентации каждого ребра ℤd + 1 в направлении увеличения значения координаты.
В Закон больших чисел на целых числах
Закон больших чисел для числа частиц в процессе целых чисел неформально означает, что для всех больших , примерно равно для некоторой положительной постоянной . Тед Харрис (1974) доказали, что если процесс выживает, то скорость роста максимально и по крайней мере линейно во времени. Слабый закон больших чисел (что процесс сходится по вероятности ) был показан Durrett (1980). Несколькими годами позже Даррет и Гриффит (1983) улучшили это до строгого закона больших чисел, давая почти верная сходимость процесса.
Вымирают при критичности
Для контактного процесса на всех целочисленных решетках большой прорыв[нужна цитата ] пришел в 1990 году, когда Безёйденхаут и Гримметт показал, что контактный процесс также почти наверняка затухает при критическом значении.[нужна цитата ]
Дарретта гипотеза и Центральная предельная теорема
Durrett предполагаемый в обзорных статьях и конспектах лекций 80-х и начала 90-х годов, касающихся Центральная предельная теорема для Харриса контактный процесс, а именно. что, если процесс выживет, то для всех больших , равно а ошибка равна умноженное на (случайную) ошибку, распределенную согласно стандарту Гауссово распределение.[1][2][3]
Дарретта догадка оказался верным для другого значения в качестве доказано в 2018 году.[4]
Рекомендации
- ^ Дарретт, Ричард (1984). «Ориентированная перколяция в двухмерном числе». Анналы вероятности. 12 (4): 999–1040. Дои:10.1214 / aop / 1176993140.
- ^ Даррет, Ричард. «Конспект лекций по системам частиц и перколяции». Wadsworth.
- ^ .Даррет, Ричард. «Контактный процесс, 1974–1989». Корнельский университет, Институт математических наук.
- ^ Циуфас, Ахиллефы (2018). "Центральная предельная теорема для суперкритической ориентированной перколяции в двух измерениях". Журнал статистической физики. 171 (5): 802–821. arXiv:1411.4543. Дои:10.1007 / s10955-018-2040-г.
- К. Безёйденхаут и Г. Р. Гримметт, Критический контактный процесс умирает, Анна. Вероятно. 18 (1990), 1462–1482.
- Дарретт, Ричард (1980). «О росте одномерных контактных процессов». Анналы вероятности. 8 (5): 890–907. Дои:10.1214 / aop / 1176994619.
- Дарретт, Ричард (1988). «Конспект лекций по системам частиц и перколяции», Уодсворт.
- Дарретт, Ричард (1991). «Контактный процесс, 1974–1989». Корнельский университет, Институт математических наук.
- Дарретт, Ричард (1984). «Ориентированная перколяция в двухмерном числе». Анналы вероятности. 12 (4): 999–1040. Дои:10.1214 / aop / 1176993140.
- Дарретт, Ричард; Дэвид Гриффит (1983). «Сверхкритические контактные процессы на Z». Анналы вероятности. 11 (1): 1–15. Дои:10.1214 / aop / 1176993655.
- Гриммет, Джеффри (1999), Перколяция, Springer
- Лиггетт, Томас М. (1985). Системы взаимодействующих частиц. Нью-Йорк: Springer Verlag. ISBN 978-0-387-96069-2.
- Томас М. Лиггетт, "Стохастические взаимодействующие системы: процессы контакта, голосования и исключения", Springer-Verlag, 1999.
























