Гиперграф - Hypergraph

Пример гиперграфа с ${\displaystyle X=\{v_{1},v_{2},v_{3},v_{4},v_{5},v_{6},v_{7}\}}$ и ${\displaystyle E=\{e_{1},e_{2},e_{3},e_{4}\}=}$ ${\displaystyle \{\{v_{1},v_{2},v_{3}\},}$ ${\displaystyle \{v_{2},v_{3}\},}$ ${\displaystyle \{v_{3},v_{5},v_{6}\},}$ ${\displaystyle \{v_{4}\}\}}$. Этот гиперграф имеет порядок 7 и размер 4. Здесь ребра соединяют не только две вершины, а несколько, и представлены цветами.

Альтернативное представление гиперграфа, представленного на рисунке выше, называется PAOH.^[1] Ребра - это вертикальные линии, соединяющие вершины. Вершины выровнены по левому краю. В легенде справа показаны названия ребер.

В математика, а гиперграф является обобщением график в котором край может присоединиться к любому количеству вершины. Напротив, в обычном графе ребро соединяет ровно две вершины. Формально гиперграф ${\displaystyle H}$ пара ${\displaystyle H=(X,E)}$ куда ${\displaystyle X}$ это набор элементов, называемый узлы или же вершины, и ${\displaystyle E}$ представляет собой набор непустых подмножеств ${\displaystyle X}$ называется гиперребра или же края. Следовательно, ${\displaystyle E}$ это подмножество ${\displaystyle {\mathcal {P}}(X)\setminus \{\emptyset \}}$, куда ${\displaystyle {\mathcal {P}}(X)}$ это набор мощности из ${\displaystyle X}$. Размер множества вершин называется порядок гиперграфа, а размер набора ребер равен размер гиперграфа.

В то время как ребра графа представляют собой двухэлементные подмножества узлов, гиперребра представляют собой произвольные наборы узлов и, следовательно, могут содержать произвольное количество узлов. Однако часто бывает желательно изучать гиперграфы, в которых все гиперребра имеют одинаковую мощность; а k-равномерный гиперграф гиперграф такой, что все его гиперребра имеют размер k. (Другими словами, один такой гиперграф представляет собой набор множеств, каждое из которых является гиперребром, соединяющим k узлов.) Таким образом, 2-однородный гиперграф - это граф, 3-однородный гиперграф - это набор неупорядоченных троек и т. д. Гиперграф также называют установить систему или семейство наборов взяты из универсальный набор.

Гиперграфы можно рассматривать как структуры падения. В частности, существует двудольный «граф инцидентности» или «Граф Леви "соответствующий каждому гиперграфу, и, наоборот, большинство, но не все, двудольные графы можно рассматривать как графы инцидентности гиперграфов.

У гиперграфов много других названий. В вычислительная геометрия, гиперграф иногда можно назвать пространство диапазона и тогда гиперребра называются диапазоны.^[2]В кооперативная игра теории гиперграфы называются простые игры (игры с голосованием); это понятие применяется для решения проблем в теория социального выбора. В некоторой литературе края обозначаются как гиперссылки или же разъемы.^[3]

Коллекция гиперграфов представляет собой категория с гиперграфом гомоморфизмы в качестве морфизмы.

Свойства гиперграфов

Гиперграф может иметь различные свойства, например:

• Пустой - не имеет краев.
• Непростой (или же несколько) - имеет петли (гиперребра с одной вершиной) или повторяющиеся ребра, что означает, что может быть два или более ребер, содержащих один и тот же набор вершин.
• Простой - не имеет петель и повторяющихся краев.
• ${\displaystyle d}$-обычный - каждая вершина имеет степень ${\displaystyle d}$, т.е. содержится ровно в ${\displaystyle d}$ гиперребра.
• 2-цветный - его вершины можно разделить на два класса U и V таким образом, чтобы каждое гиперребро мощности не менее 2 содержало хотя бы одну вершину из обоих классов. Альтернативный термин Свойство B.
  • Два более сильных свойства: двудольный и сбалансированный.
• ${\displaystyle k}$-униформа - каждое гиперребро содержит ровно ${\displaystyle k}$ вершины.
• ${\displaystyle k}$-частный - вершины разбиты на ${\displaystyle k}$ частей, и каждое гиперребро содержит ровно по одной вершине каждого типа.
  • Каждый ${\displaystyle k}$-частный гиперграф (для ${\displaystyle k\geq 2}$) оба ${\displaystyle k}$-однородные и двудольные (и двухцветные).
• Закрыто вниз - каждое подмножество гиперребра также является гиперребром. Замкнутый вниз гиперграф обычно называют абстрактный симплициальный комплекс.
  • Абстрактный симплициальный комплекс с дополнительным свойством, называемым свойство увеличения называется матроид.

Связанные гиперграфы

Поскольку гиперграфические ссылки могут иметь любую мощность, существует несколько понятий концепции подграфа, называемых подгиперграфы, частичные гиперграфы и секционные гиперграфы.

Позволять ${\displaystyle H=(X,E)}$ - гиперграф, состоящий из вершин

${\displaystyle X=\lbrace x_{i}\mid i\in I_{v}\rbrace ,}$

и имея набор кромок

${\displaystyle E=\lbrace e_{i}\mid i\in I_{e}\land e_{i}\subseteq X\land e_{i}\neq \emptyset \rbrace ,}$

куда ${\displaystyle I_{v}}$ и ${\displaystyle I_{e}}$ являются наборы индексов вершин и ребер соответственно.

А подгиперграф - гиперграф с удаленными вершинами. Формально подгиперграф ${\displaystyle H_{A}}$ индуцированный ${\displaystyle A\subseteq X}$ определяется как

${\displaystyle H_{A}=\left(A,\lbrace e\cap A\mid e\in E\land e\cap A\neq \emptyset \rbrace \right).}$

Альтернативный термин - ограничение ЧАС к А.^[4]:468

An расширение подгиперграфа гиперграф, в котором каждое гиперребро ${\displaystyle H}$ который частично содержится в подгиперграфе ${\displaystyle H_{A}}$ полностью содержится в расширении ${\displaystyle Ex(H_{A})}$. Формально

${\displaystyle Ex(H_{A})=(A\cup A',E')}$ с ${\displaystyle A'=\bigcup _{e\in E}e\setminus A}$ и ${\displaystyle E'=\lbrace e\in E\mid e\subseteq (A\cup A')\rbrace }$.

В частичный гиперграф - гиперграф с удаленными ребрами.^[4]:468 Учитывая подмножество ${\displaystyle J\subset I_{e}}$ набора индексов ребер частичный гиперграф, порожденный ${\displaystyle J}$ гиперграф

${\displaystyle \left(X,\lbrace e_{i}\mid i\in J\rbrace \right).}$

Учитывая подмножество ${\displaystyle A\subseteq X}$, то секционный гиперграф частичный гиперграф

${\displaystyle H\times A=\left(A,\lbrace e_{i}\mid i\in I_{e}\land e_{i}\subseteq A\rbrace \right).}$

В двойной ${\displaystyle H^{*}}$ из ${\displaystyle H}$ является гиперграфом, вершины и ребра которого поменяны местами, так что вершины задаются ${\displaystyle \lbrace e_{i}\rbrace }$ и чьи ребра задаются ${\displaystyle \lbrace X_{m}\rbrace }$ куда

${\displaystyle X_{m}=\lbrace e_{i}\mid x_{m}\in e_{i}\rbrace .}$

Когда понятие равенства правильно определено, как это делается ниже, операция взятия двойника гиперграфа становится инволюция, т.е.

${\displaystyle \left(H^{*}\right)^{*}=H.}$

А связный граф грамм с тем же набором вершин, что и связный гиперграф ЧАС это граф хоста за ЧАС если каждое гиперребро ЧАС побуждает связный подграф в грамм. Для несвязного гиперграфа ЧАС, грамм является хост-графом, если существует взаимное соответствие между связанные компоненты из грамм и из ЧАС, так что каждая связная компонента ГРАММ' из грамм является хозяином соответствующих ЧАС'.

В 2-х секционный (или же граф клики, представляющий граф, прямой граф, Граф Гайфмана) гиперграфа - это граф с одинаковыми вершинами гиперграфа и ребрами между всеми парами вершин, содержащимися в одном гиперребре.

Матрица заболеваемости

Позволять ${\displaystyle V=\{v_{1},v_{2},~\ldots ,~v_{n}\}}$ и ${\displaystyle E=\{e_{1},e_{2},~\ldots ~e_{m}\}}$. Каждый гиперграф имеет ${\displaystyle n\times m}$ матрица инцидентности ${\displaystyle A=(a_{ij})}$ куда

${\displaystyle a_{ij}=\left\{{\begin{matrix}1&\mathrm {if} ~v_{i}\in e_{j}\\0&\mathrm {otherwise} .\end{matrix}}\right.}$

В транспонировать ${\displaystyle A^{t}}$ из заболеваемость матрица определяет гиперграф ${\displaystyle H^{*}=(V^{*},\ E^{*})}$ называется двойной из ${\displaystyle H}$, куда ${\displaystyle V^{*}}$ является м-элементный набор и ${\displaystyle E^{*}}$ является п-элементный набор подмножеств ${\displaystyle V^{*}}$. За ${\displaystyle v_{j}^{*}\in V^{*}}$ и ${\displaystyle e_{i}^{*}\in E^{*},~v_{j}^{*}\in e_{i}^{*}}$ если и только если ${\displaystyle a_{ij}=1}$.

График заболеваемости

Гиперграф ЧАС может быть представлен двудольный граф BG следующим образом: множества Икс и E являются перегородками BG, и (Икс₁, е₁) связаны с ребром тогда и только тогда, когда вершина Икс₁ содержится в краю е₁ в ЧАС.

И наоборот, любой двудольный граф с фиксированными частями и без несвязанных узлов во второй части представляет собой некоторый гиперграф, как описано выше. Этот двудольный граф также называют график заболеваемости.

Циклы

В отличие от обычных неориентированных графов, для которых существует единственное естественное понятие циклы и ациклические графы, существует несколько естественных неэквивалентных определений ацикличности для гиперграфов, которые коллапсируют до ацикличности обычного графа в частном случае обычных графов.

Первое определение ацикличности для гиперграфов было дано Клод Берже:^[5] гиперграф является ацикличным по Берже, если его график заболеваемости (в двудольный граф определено выше) является ациклическим. Это определение очень ограничительное: например, если в гиперграфе есть пара ${\displaystyle v\neq v'}$ вершин и некоторой пары ${\displaystyle f\neq f'}$ гиперребер такие, что ${\displaystyle v,v'\in f}$ и ${\displaystyle v,v'\in f'}$, то он цикличен по Берже. Цикличность по Берже, очевидно, можно проверить в линейное время исследованием графика заболеваемости.

Мы можем определить более слабое понятие ацикличности гиперграфа,^[6] позже названный α-ацикличностью. Это понятие ацикличности эквивалентно конформности гиперграфа (каждая клика прямого графа покрыта некоторым гиперребром) и его прямому графу. хордовый; это также эквивалентно сводимости к пустому графу через алгоритм GYO^[7][8] (также известный как алгоритм Грэма), сливаться итерационный процесс, который удаляет гиперребра с использованием обобщенного определения уши. В области теория баз данных, известно, что схема базы данных обладает определенными желательными свойствами, если лежащий в основе гиперграф является α-ациклическим.^[9] Кроме того, α-ацикличность также связана с выраженностью охраняемый фрагмент из логика первого порядка.

Мы можем протестировать в линейное время если гиперграф α-ацикличен.^[10]

Обратите внимание, что α-ацикличность имеет противоречивое свойство: добавление гиперребер к α-циклическому гиперграфу может сделать его α-ациклическим (например, добавление гиперребра, содержащего все вершины гиперграфа, всегда будет делать его α-ациклическим). Частично мотивированные этим предполагаемым недостатком, Рональд Феджин^[11] определили более сильные понятия β-ацикличности и γ-ацикличности. Мы можем сформулировать β-ацикличность как требование, чтобы все подгиперграфы гиперграфа были α-ацикличными, что эквивалентно^[11] к более раннему определению Грэма.^[8] Понятие γ-ацикличности является более ограничивающим условием, которое эквивалентно нескольким желательным свойствам схем базы данных и связано с Диаграммы Бахмана. Как β-ацикличность, так и γ-ацикличность могут быть проверены в полиномиальное время.

Эти четыре понятия ацикличности сопоставимы: ацикличность по Берже подразумевает γ-ацикличность, которая подразумевает β-ацикличность, которая подразумевает α-ацикличность. Однако обратных выводов нет, поэтому эти четыре понятия различны.^[11]

Изоморфизм и равенство

Гиперграф гомоморфизм - это отображение множества вершин одного гиперграфа на другой, так что каждое ребро отображается на одно другое ребро.

Гиперграф ${\displaystyle H=(X,E)}$ является изоморфный к гиперграфу ${\displaystyle G=(Y,F)}$, записанный как ${\displaystyle H\simeq G}$ если существует биекция

${\displaystyle \phi :X\to Y}$

и перестановка ${\displaystyle \pi }$ из ${\displaystyle I}$ такой, что

${\displaystyle \phi (e_{i})=f_{\pi (i)}}$

Биекция ${\displaystyle \phi }$ затем называется изоморфизм графиков. Обратите внимание, что

${\displaystyle H\simeq G}$ если и только если ${\displaystyle H^{*}\simeq G^{*}}$.

Когда ребра гиперграфа помечены явно, появляется дополнительное понятие сильный изоморфизм. Один говорит, что ${\displaystyle H}$ является сильно изоморфный к ${\displaystyle G}$ если перестановка тождественна. Затем один пишет ${\displaystyle H\cong G}$. Обратите внимание, что все сильно изоморфные графы изоморфны, но не наоборот.

Когда вершины гиперграфа помечены явно, есть понятия эквивалентность, а также равенство. Один говорит, что ${\displaystyle H}$ является эквивалент к ${\displaystyle G}$, и пишет ${\displaystyle H\equiv G}$ если изоморфизм ${\displaystyle \phi }$ имеет

${\displaystyle \phi (x_{n})=y_{n}}$

и

${\displaystyle \phi (e_{i})=f_{\pi (i)}}$

Обратите внимание, что

${\displaystyle H\equiv G}$ если и только если ${\displaystyle H^{*}\cong G^{*}}$

Если, кроме того, перестановка ${\displaystyle \pi }$ это личность, говорят, что ${\displaystyle H}$ равно ${\displaystyle G}$, и пишет ${\displaystyle H=G}$. Обратите внимание, что с этим определением равенства графы самодвойственны:

${\displaystyle \left(H^{*}\right)^{*}=H}$

Гиперграф автоморфизм является изоморфизмом множества вершин в себя, то есть перемаркировкой вершин. Множество автоморфизмов гиперграфа ЧАС (= (Икс, E)) это группа по составу, названный группа автоморфизмов гиперграфа и написанного Aut (ЧАС).

Примеры

Рассмотрим гиперграф ${\displaystyle H}$ с краями

${\displaystyle H=\lbrace e_{1}=\lbrace a,b\rbrace ,e_{2}=\lbrace b,c\rbrace ,e_{3}=\lbrace c,d\rbrace ,e_{4}=\lbrace d,a\rbrace ,e_{5}=\lbrace b,d\rbrace ,e_{6}=\lbrace a,c\rbrace \rbrace }$

и

${\displaystyle G=\lbrace f_{1}=\lbrace \alpha ,\beta \rbrace ,f_{2}=\lbrace \beta ,\gamma \rbrace ,f_{3}=\lbrace \gamma ,\delta \rbrace ,f_{4}=\lbrace \delta ,\alpha \rbrace ,f_{5}=\lbrace \alpha ,\gamma \rbrace ,f_{6}=\lbrace \beta ,\delta \rbrace \rbrace }$

Тогда ясно ${\displaystyle H}$ и ${\displaystyle G}$ изоморфны (с ${\displaystyle \phi (a)=\alpha }$, и Т. Д.), но они не сильно изоморфны. Так, например, в ${\displaystyle H}$, вершина ${\displaystyle a}$ встречается с ребрами 1, 4 и 6, так что,

${\displaystyle e_{1}\cap e_{4}\cap e_{6}=\lbrace a\rbrace }$

В графике ${\displaystyle G}$, не существует вершины, которая пересекает ребра 1, 4 и 6:

${\displaystyle f_{1}\cap f_{4}\cap f_{6}=\varnothing }$

В этом примере ${\displaystyle H}$ и ${\displaystyle G}$ эквивалентны, ${\displaystyle H\equiv G}$, причем двойственные сильно изоморфны: ${\displaystyle H^{*}\cong G^{*}}$.

Симметричные гиперграфы

В классифицировать ${\displaystyle r(H)}$ гиперграфа ${\displaystyle H}$ - максимальная мощность любого из ребер гиперграфа. Если все ребра имеют одинаковую мощность k, гиперграф называется униформа или же k-униформа, или называется k-гиперграф. Граф - это просто 2-равномерный гиперграф.

Степень d (v) вершины v количество ребер, которые его содержат. ЧАС является k-обычный если каждая вершина имеет степень k.

Двойник равномерного гиперграфа регулярен, и наоборот.

Две вершины Икс и у из ЧАС называются симметричный если существует автоморфизм такой, что ${\displaystyle \phi (x)=y}$. Два края ${\displaystyle e_{i}}$ и ${\displaystyle e_{j}}$ как говорят симметричный если существует автоморфизм такой, что ${\displaystyle \phi (e_{i})=e_{j}}$.

Гиперграф называется вершинно-транзитивный (или же вершинно-симметричный), если все его вершины симметричны. Аналогично гиперграф - это реберно-транзитивный если все ребра симметричны. Если гиперграф является реберно-симметричным и вершинно-симметричным, то гиперграф просто переходный.

Из-за двойственности гиперграфов изучение транзитивности ребер идентично изучению транзитивности вершин.

Обобщения понятий из графов

Много теоремы и концепции, связанные с графами, также применимы к гиперграфам, в частности:

• Соответствие в гиперграфах;
• Крышка Vertex в гиперграфах (также известный как: поперечный);
• Линейный график гиперграфа;
• Гиперграф грамматика - создается путем дополнения класса гиперграфов набором правил замены;
• Теорема Рамсея;
• Теорема Эрдеша – Ко – Радо.;
• Теорема Крускала – Катоны на однородных гиперграфах;
• Теоремы холловского типа для гиперграфов.

Раскраска гиперграфа

Классическая раскраска гиперграфа - это присвоение одного из цветов из набора ${\displaystyle \{1,2,3,...\lambda \}}$ в каждую вершину гиперграфа таким образом, чтобы каждое гиперребро содержало не менее двух вершин разных цветов. Другими словами, не должно быть одноцветного гиперребра с мощностью не меньше 2. В этом смысле это прямое обобщение раскраски графа. Минимальное количество используемых различных цветов для всех раскрасок называется хроматическим числом гиперграфа.

Гиперграфы, для которых существует раскраска с точностью до k цвета называются k-раскрашиваемый. Двукратные гиперграфы - это в точности двудольные.

Есть много обобщений классической раскраски гиперграфов. Один из них - это так называемая смешанная раскраска гиперграфа, когда допускаются одноцветные ребра. Некоторые смешанные гиперграфы невозможно раскрасить в любое количество цветов. Общий критерий неокрашиваемости неизвестен. Когда смешанный гиперграф можно раскрашивать, минимальное и максимальное количество используемых цветов называются нижним и верхним хроматическими числами соответственно. Видеть http://spectrum.troy.edu/voloshin/mh.html для подробностей.

Перегородки

Теорема о разбиении Э. Даубера^[12] утверждает, что для гиперграфа с транзитивным ребром ${\displaystyle H=(X,E)}$, существует раздел

${\displaystyle (X_{1},X_{2},\cdots ,X_{K})}$

множества вершин ${\displaystyle X}$ так что подгиперграф ${\displaystyle H_{X_{k}}}$ создано ${\displaystyle X_{k}}$ транзитивен для каждого ${\displaystyle 1\leq k\leq K}$, и такой, что

${\displaystyle \sum _{k=1}^{K}r\left(H_{X_{k}}\right)=r(H)}$

куда ${\displaystyle r(H)}$ это ранг ЧАС.

Как следствие, реберно-транзитивный гиперграф, который не является вершинно-транзитивным, является бикрасильным.

Разбиение графа (и, в частности, разбиение гиперграфов) имеет множество приложений для проектирования микросхем.^[13] и параллельные вычисления.^[14][15][16] Эффективный и масштабируемый алгоритмы разбиения гиперграфа также важны для обработки крупномасштабных гиперграфов в задачах машинного обучения.^[17]

Рисунок гиперграфа

Этот принципиальная электрическая схема можно интерпретировать как рисунок гиперграфа, в котором четыре вершины (изображенные в виде белых прямоугольников и дисков) соединены тремя гиперребрами, изображенными в виде деревьев.

Хотя гиперграфы сложнее рисовать на бумаге, чем графики, несколько исследователей изучали методы визуализации гиперграфов.

В одном возможном визуальном представлении гиперграфов, аналогичном стандартному рисунок графика стиль, в котором кривые на плоскости используются для изображения ребер графа, вершины гиперграфа изображаются как точки, диски или коробки, а его гиперребра изображаются как деревья, вершины которых являются их листьями.^[18][19] Если вершины представлены в виде точек, гиперребра могут также отображаться как гладкие кривые, соединяющие наборы точек, или как простые замкнутые кривые которые включают наборы точек.^[20][21][22]

Диаграмма Венна четвертого порядка, которую можно интерпретировать как разбиение гиперграфа с 15 вершинами (15 цветных областей) и 4 гиперребрами (4 эллипса).

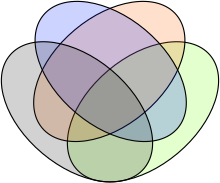
В другом стиле визуализации гиперграфа, модель подразделения рисования гиперграфа,^[23] плоскость разбита на области, каждая из которых представляет одну вершину гиперграфа. Гиперребра гиперграфа представлены смежными подмножествами этих областей, которые могут быть обозначены раскраской, рисованием контуров вокруг них или и тем, и другим. Заказ-п Диаграмма Венна, например, может рассматриваться как рисунок с разбивкой гиперграфа с п гиперребер (кривые, определяющие диаграмму) и 2^п - 1 вершина (представленная областями, на которые эти кривые делят плоскость). В отличие от распознавания за полиномиальное время планарные графы, это НП-полный чтобы определить, есть ли у гиперграфа чертеж плоского подразделения,^[24] но наличие рисунка этого типа может быть эффективно проверено, когда шаблон смежности регионов ограничен путем, чтобы быть путем, циклом или деревом.^[25]

Альтернативное представление гиперграфа под названием PAOH^[1] показано на рисунке в верхней части этой статьи. Ребра - это вертикальные линии, соединяющие вершины. Вершины выровнены по левому краю. В легенде справа показаны названия ребер. Он был разработан для динамических гиперграфов, но может использоваться и для простых гиперграфов.

Обобщения

Одно из возможных обобщений гиперграфа - позволить ребрам указывать на другие ребра. Есть два варианта этого обобщения. В одном ребра состоят не только из набора вершин, но также могут содержать подмножества вершин, подмножества подмножеств вершин и т. Д. до бесконечности. По сути, каждое ребро - это просто внутренний узел дерева или ориентированный ациклический граф, а вершины - это листовые узлы. Тогда гиперграф - это просто набор деревьев с общими общими узлами (то есть, данный внутренний узел или лист может встречаться в нескольких разных деревьях). И наоборот, любой набор деревьев можно понимать как этот обобщенный гиперграф. Поскольку деревья широко используются повсюду Информатика и многие другие разделы математики, можно сказать, что гиперграфы также возникают естественным образом. Так, например, это обобщение естественно возникает как модель алгебра терминов; ребра соответствуют термины а вершины соответствуют константам или переменным.

Для такого гиперграфа членство в множестве затем обеспечивает упорядочение, но оно не является ни частичный заказ ни Предварительный заказ, поскольку он не транзитивен. Граф, соответствующий графу Леви этого обобщения, является ориентированный ациклический граф. Рассмотрим, например, обобщенный гиперграф, множество вершин которого ${\displaystyle V=\{a,b\}}$ и чьи края ${\displaystyle e_{1}=\{a,b\}}$ и ${\displaystyle e_{2}=\{a,e_{1}\}}$. Тогда, хотя ${\displaystyle b\in e_{1}}$ и ${\displaystyle e_{1}\in e_{2}}$, это неправда, что ${\displaystyle b\in e_{2}}$. Тем не менее переходное закрытие членства в множестве таких гиперграфов действительно индуцирует частичный заказ, и "сглаживает" гиперграф в частично заказанный набор.

В качестве альтернативы, ребрам можно разрешить указывать на другие ребра, независимо от требования, чтобы ребра были упорядочены как ориентированные ациклические графы. Это позволяет создавать графы с ребрами-петлями, которые вообще не должны содержать вершин. Например, рассмотрим обобщенный гиперграф, состоящий из двух ребер ${\displaystyle e_{1}}$ и ${\displaystyle e_{2}}$, и нулевые вершины, так что ${\displaystyle e_{1}=\{e_{2}\}}$ и ${\displaystyle e_{2}=\{e_{1}\}}$. Поскольку этот цикл бесконечно рекурсивен, множества, являющиеся ребрами, нарушают аксиома основания. В частности, для таких гиперграфов не существует транзитивного замыкания членства во множествах. Хотя такие структуры могут сначала показаться странными, их можно легко понять, заметив, что эквивалентное обобщение их графа Леви больше не двудольный, а скорее всего лишь несколько общих ориентированный граф.

Обобщенная матрица инцидентности для таких гиперграфов по определению является квадратной матрицей с рангом, равным общему количеству вершин плюс ребра. Таким образом, для приведенного выше примера матрица инцидентности просто

${\displaystyle \left[{\begin{matrix}0&1\\1&0\end{matrix}}\right].}$

Обучение гиперграфу

Гиперграфы широко используются в машинное обучение задачи как модель данных и классификатор регуляризация (математика).^[26] Приложения включают рекомендательная система (сообщества как гиперребры),^[27] поиск изображений (корреляции в виде гиперребер),^[28] и биоинформатика (биохимические взаимодействия в виде гиперребер).^[29] Репрезентативные методы обучения гиперграфу включают гиперграф спектральная кластеризация что расширяет спектральная теория графов с гиперграфом лапласианом,^[30] и гиперграф полу-контролируемое обучение это вводит дополнительную структурную стоимость гиперграфа, чтобы ограничить результаты обучения.^[31] Для крупномасштабных гиперграфов распределенная структура^[17] построен с использованием Apache Spark также доступен.

Смотрите также

• Комбинаторный дизайн
• Факторный график
• Жадоид
• Структура заболеваемости
• Мультиграф
• Система P
• Умножение разреженной матрицы на вектор

Примечания

1. Вальдивия, Паола; Буоно, Паоло; Плезан, Екатерина; Дюфурно, Николь; Фекете, Жан-Даниэль (2020). «Анализ динамических гиперграфов с помощью параллельной агрегированной упорядоченной визуализации гиперграфов» (PDF). IEEE Transactions по визуализации и компьютерной графике. IEEE. 26: 12. Дои:10.1109 / TVCG.2019.2933196. eISSN  1941-0506. ISSN  1077-2626. PMID  31398121.
2. Хаусслер, Дэвид; Вельцль, Эмо (1987), "ε-сети и симплексные запросы диапазона", Дискретная и вычислительная геометрия, 2 (2): 127–151, Дои:10.1007 / BF02187876, МИСТЕР  0884223.
3. Жемчужина Иудеи, в ЭВРИСТИКА Стратегии интеллектуального поиска для решения компьютерных проблем, Эддисон Уэсли (1984), стр. 25.
4. Ловас, Ласло; Пламмер, М. (1986), Теория соответствия, Анналы дискретной математики, 29, Северная Голландия, ISBN  0-444-87916-1, МИСТЕР  0859549
5. Берже, Клод (1973). Графы и гиперграфы. Амстердам: Северная Голландия. ISBN  0-7204-2450-X.
6. Beeri, C .; Феджин, Р.; Maier, D .; Яннакакис, М. (1983). «О желательности ациклических схем баз данных». Журнал ACM. 30 (3): 479–513. Дои:10.1145/2402.322389.
7. Yu, C.T .; Озсойоглу, М. З. (1979). «Алгоритм членства в древовидном запросе распределенного запроса» (PDF). Proc. IEEE COMPSAC: 306–312.
8. Грэм, М. Х. (1979). «Об универсальном отношении». Технический отчет. Торонто, Онтарио, Канада: Университет Торонто.
9. Абитебул, С.; Халл, Р. Б.; Виану, В. (1995). Основы баз данных. Эддисон-Уэсли. ISBN  0-201-53771-0.
10. Тарьян, Р.Э.; Яннакакис, М. (1984). «Простые алгоритмы линейного времени для проверки хордальности графов, проверки ацикличности гиперграфов и выборочного сокращения ациклических гиперграфов». SIAM Журнал по вычислениям. 13 (3): 566–579. Дои:10.1137/0213035.
11. Феджин, Рональд (1983). «Степени ацикличности для гиперграфов и схем реляционных баз данных». Журнал ACM. 30 (3): 514–550. Дои:10.1145/2402.322390.
12. Э. Даубер, в Теория графов, изд. Ф. Харари, Эддисон Уэсли, (1969) стр. 172.
13. Карипис, Г., Аггарвал, Р., Кумар, В., и Шекхар, С. (март 1999 г.), "Многоуровневое разбиение гиперграфа: приложения в области СБИС", Транзакции IEEE в системах с очень крупномасштабной интеграцией (СБИС), 7 (1): 69–79, CiteSeerX  10.1.1.553.2367, Дои:10.1109/92.748202.
14. Хендриксон, Б., Колда, Т.Г. (2000), «Модели разбиения графов для параллельных вычислений», Параллельные вычисления (Представлена ​​рукопись), 26 (12): 1519–1545, Дои:10.1016 / S0167-8191 (00) 00048-X.
15. Catalyurek, U.V .; Айканат, К. (1995). Модель гиперграфа для отображения повторяющихся вычислений разреженных матрично-векторных произведений на мультикомпьютеры. Proc. Международная конференция по высокопроизводительным вычислениям (HiPC'95).
16. Catalyurek, U.V .; Айканат, К. (1999), "Декомпозиция на основе гиперграфа для параллельного умножения векторов разреженной матрицы", Транзакции IEEE в параллельных и распределенных системах, 10 (7): 673–693, CiteSeerX  10.1.1.67.2498, Дои:10.1109/71.780863.
17. Хуанг, Цзинь; Чжан, Руи; Ю, Джеффри Сюй (2015), «Масштабируемое обучение и обработка гиперграфов», Материалы Международной конференции IEEE по интеллектуальному анализу данных
18. Сандер, Г. (2003), «Схема ориентированных гиперграфов с ортогональными гиперребрами», Proc. 11-й Международный симпозиум по графическому рисованию (GD 2003), Конспект лекций по информатике, 2912, Springer-Verlag, стр. 381–386..
19. Эшбах, Томас; Гюнтер, Вольфганг; Беккер, Бернд (2006), «Отрисовка ортогонального гиперграфа для улучшения видимости» (PDF), Журнал графических алгоритмов и приложений, 10 (2): 141–157, Дои:10.7155 / jgaa.00122.
20. Мякинен, Эркки (1990), «Как нарисовать гиперграф», Международный журнал компьютерной математики, 34 (3): 177–185, Дои:10.1080/00207169008803875.
21. Берто, Франсуа; Идс, Питер (2001), «Рисование гиперграфов в стандарте подмножества», Proc. 8-й Международный симпозиум по графическому рисованию (GD 2000), Конспект лекций по информатике, 1984, Springer-Verlag, стр. 45–76, Дои:10.1007/3-540-44541-2_15, ISBN  978-3-540-41554-1.
22. Нахид Анджум, Арафат; Брессан, Стефан (2017), «Рисунок гиперграфа путем размещения под действием силы», 28-я Международная конференция по приложениям баз данных и экспертных систем (DEXA 2017), Конспект лекций по информатике, 10439, Springer International Publishing, стр. 387–394, Дои:10.1007/978-3-319-64471-4_31, ISBN  978-3-319-64470-7.
23. Кауфманн, Майкл; ван Кревельд, Марк; Спекманн, Беттина (2009), «Чертежи разбиения гиперграфов», Proc. 16-й Международный симпозиум по графическому рисованию (GD 2008), Конспект лекций по информатике, 5417, Springer-Verlag, стр. 396–407, Дои:10.1007/978-3-642-00219-9_39, ISBN  978-3-642-00218-2.
24. Джонсон, Дэвид С.; Поллак, Х. О. (2006), "Планарность гиперграфа и сложность построения диаграмм Венна", Журнал теории графов, 11 (3): 309–325, Дои:10.1002 / jgt.3190110306.
25. Бучин, Кевин; ван Кревельд, Марк; Мейер, Хенк; Спекманн, Беттина; Verbeek, Кевин (2010), "О планарных носителях для гиперграфов", Proc. 17-й Международный симпозиум по графическому рисованию (GD 2009), Конспект лекций по информатике, 5849, Springer-Verlag, стр. 345–356, Дои:10.1007/978-3-642-11805-0_33, ISBN  978-3-642-11804-3.
26. Чжоу, Дэнъюн; Хуанг, Цзяюань; Scholkopf, Bernhard (2006), "Обучение с помощью гиперграфов: кластеризация, классификация и вложение", Достижения в системах обработки нейронной информации (2): 1601–1608
27. Тан, Шулонг; Бу, Цзяцзюнь; Чен, Чун; Сюй, Бен; Ван, Джан; Он, Сяофэй (2013), «Использование обширной информации из социальных сетей для рекомендации музыки с помощью модели гиперграфа», ACM-транзакции в мультимедийных вычислениях, коммуникациях и приложениях (1), Bibcode:2011smma.book..213T
28. Лю, Циншань; Хуанг, Ючи; Метаксас, Димитрис Н. (2013), «Гиперграф с выборкой для поиска изображений», Распознавание образов, 44 (10–11): 2255–2262, Дои:10.1016 / j.patcog.2010.07.014
29. Патро, Роб; Кингсфорд, Карл (2013), «Прогнозирование белковых взаимодействий с помощью экономного вывода истории сети», Биоинформатика, 29 (10–11): 237–246, Дои:10.1093 / биоинформатика / btt224, ЧВК  3694678, PMID  23812989
30. Гао, Вт; Ван, Мэн; Чжа, Чжэн-Цзюнь; Шен, Цзяли; Ли, Сюэлун; У, Синьдун (2013), «Совместное визуально-текстовое изучение релевантности для поиска изображений в социальных сетях на основе тегов», IEEE Transactions по обработке изображений, 22 (1): 363–376, Bibcode:2013ITIP ... 22..363л., Дои:10.1109 / tip.2012.2202676, PMID  22692911, S2CID  7432373
31. Тиан, Цзэ; Хван, Тэ Хён; Куанг, Руи (2009), «Алгоритм обучения на основе гиперграфа для классификации экспрессии генов и данных arrayCGH с предварительным знанием», Биоинформатика, 25 (21): 2831–2838, Дои:10.1093 / биоинформатика / btp467, PMID  19648139

Рекомендации

• Клод Берже, "Гиперграфы: комбинаторика конечных множеств". Северная Голландия, 1989 г.
• Клод Бердж, Диджен Рэй-Чаудхури, «Семинар по гиперграфу, Университет штата Огайо, 1972 год», Конспект лекций по математике 411 Springer-Verlag
• «Гиперграф», Энциклопедия математики, EMS Press, 2001 [1994]
• Ален Бретто, "Теория гиперграфа: введение", Springer, 2013.
• Виталий Иванович Волошин. «Раскраска смешанных гиперграфов: теория, алгоритмы и приложения». Монографии Института Филдса, Американское математическое общество, 2002.
• Виталий Иванович Волошин. «Введение в теорию графов и гиперграфов». Nova Science Publishers, Inc., 2009.
• В этой статье использованы материалы из гиперграф на PlanetMath, который находится под лицензией Лицензия Creative Commons Attribution / Share-Alike.

внешняя ссылка

• PAOHVis: система с открытым исходным кодом PAOHVis для визуализации динамических гиперграфов.