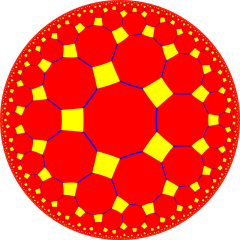
Порядок-4 додекаэдрические соты - Order-4 dodecahedral honeycomb

Порядок-4 додекаэдрические соты

Тип	Гиперболические обычные соты Равномерные гиперболические соты
Символ Шлефли	{5,3,4} {5,3^1,1}
Диаграмма Кокстера	↔
Клетки	{5,3}
Лица	пятиугольник {5}
Край фигура	квадрат {4}
Фигура вершины	октаэдр
Двойной	Заказать-5 соты куб.
Группа Кокстера	${displaystyle {overline {BH}} _ {3}}$ , [4,3,5] ${displaystyle {overline {DH}} _ {3}}$ , [5,3^1,1]
Характеристики	Обычный, Квазирегулярные соты

в геометрия из гиперболическое 3-пространство, то додекаэдрические соты порядка 4 один из четырех компактных обычный заполнение пространства мозаика (или же соты ). С Символ Шлефли {5,3,4}, в нем четыре додекаэдр вокруг каждого ребра и 8 додекаэдров вокруг каждой вершины в восьмигранный расположение. Его вершины построены из 3-х ортогональных осей. Его двойной это порядка-5 кубических сот.

А геометрические соты это заполнение пространства из многогранник или многомерный клетки, чтобы не было зазоров. Это пример более общего математического черепица или же мозаика в любом количестве измерений.

Соты обычно строятся из обычных Евклидово ("плоское") пространство, как и выпуклые однородные соты. Они также могут быть построены в неевклидовы пространства, Такие как гиперболические однородные соты. Любой конечный равномерный многогранник можно спроецировать на его окружающая сфера образовывать однородные соты в сферическом пространстве.

Описание

В двугранный угол из правильный додекаэдр составляет ~ 116,6 °, поэтому невозможно разместить 4 из них на ребре в трехмерном евклидовом пространстве. Однако в гиперболическом пространстве правильно масштабированный правильный додекаэдр можно масштабировать так, чтобы его двугранные углы уменьшились до 90 градусов, а затем четыре точно соответствовали каждому ребру.

Симметрия

Он имеет конструкцию полусимметрии, {5,3^1,1}, с двумя типами (цветами) додекаэдров в Строительство Wythoff. ↔ .

Изображений

Его можно рассматривать как аналог двумерного гиперболического Пятиугольная черепица порядка 4, {5,4}

Вид на додекаэдрические соты порядка 4 под Модель Бельтрами-Кляйна

Связанные многогранники и соты

В трехмерном гиперболическом пространстве есть четыре регулярных компактных соты:

Четыре обычных компактных соты в H³
{5,3,4}	{4,3,5}	{3,5,3}	{5,3,5}

Есть пятнадцать однородных сот в [5,3,4] Группа Кокстера семья, включая эту обычную форму.

[5,3,4] семейные соты
{5,3,4}	г {5,3,4}	т {5,3,4}	рр {5,3,4}	т_0,3{5,3,4}	tr {5,3,4}	т_0,1,3{5,3,4}	т_0,1,2,3{5,3,4}


{4,3,5}	г {4,3,5}	т {4,3,5}	рр {4,3,5}	2т {4,3,5}	tr {4,3,5}	т_0,1,3{4,3,5}	т_0,1,2,3{4,3,5}

Есть одиннадцать однородных сот в бифуркационном [5,3^1,1] Семейство группы Кокстера, включая эти соты в его альтернативной форме. Эта конструкция может быть представлена чередованием (шахматная доска) двух цветов додекаэдрических ячеек.

Эти соты также относятся к 16 ячеек, кубические соты, и гексагональные черепичные соты порядка 4 все с восьмигранными вершинами:

{p, 3,4} обычные соты
Космос	S³	E³	ЧАС³
Форма	Конечный	Аффинный	Компактный	Паракомпакт	Некомпактный
Имя	{3,3,4}	{4,3,4}	{5,3,4}	{6,3,4}	{7,3,4}	{8,3,4}	... {∞,3,4}
Изображение
Клетки	{3,3}	{4,3}	{5,3}	{6,3}	{7,3}	{8,3}	{∞,3}

Эти соты являются частью последовательности полихор и сот с додекаэдр клетки:

{5,3, п}
Космос	S³	ЧАС³
Форма	Конечный	Компактный		Паракомпакт	Некомпактный
Имя	{5,3,3}	{5,3,4}	{5,3,5}	{5,3,6}	{5,3,7}	{5,3,8}	... {5,3,∞}
Изображение
Вершина фигура	{3,3}	{3,4}	{3,5}	{3,6}	{3,7}	{3,8}	{3,∞}

Выпрямленные додекаэдрические соты порядка 4

Выпрямленные додекаэдрические соты порядка 4
Тип	Равномерные соты в гиперболическом пространстве
Символ Шлефли	г {5,3,4} г {5,3^1,1}
Диаграмма Кокстера	↔
Клетки	г {5,3} {3,4}
Лица	треугольник {3} пятиугольник {5}
Фигура вершины	квадратная призма
Группа Кокстера	${displaystyle {overline {BH}} _ {3}}$ , [4,3,5] ${displaystyle {overline {DH}} _ {3}}$ , [5,3^1,1]
Характеристики	Вершинно-транзитивный, реберный транзитивный

В выпрямленные додекаэдрические соты порядка 4, , имеет чередующиеся октаэдр и икосододекаэдр ячейки, с квадратная призма вершина фигуры.

Его можно рассматривать как аналог двумерного гиперболического четырехугольная черепица, г {5,4}

Связанные соты

Всего существует четыре выпрямленных компактных обычных соты:

Четыре выпрямленных обычных компактных сот в H³
Изображение
Символы	г {5,3,4}	г {4,3,5}	г {3,5,3}	г {5,3,5}
Вершина фигура

Усеченные додекаэдрические соты порядка 4

Усеченные додекаэдрические соты порядка 4
Тип	Равномерные соты в гиперболическом пространстве
Символ Шлефли	т {5,3,4} т {5,3^1,1}
Диаграмма Кокстера	↔
Клетки	т {5,3} {3,4}
Лица	треугольник {3} десятиугольник {10}
Фигура вершины	квадратная пирамида
Группа Кокстера	${displaystyle {overline {BH}} _ {3}}$ , [4,3,5] ${displaystyle {overline {DH}} _ {3}}$ , [5,3^1,1]
Характеристики	Вершинно-транзитивный

В додекаэдрические соты усеченного порядка 4, , имеет октаэдр и усеченный додекаэдр ячейки, с квадратная пирамида вершина фигуры.

Его можно рассматривать как аналог двумерного гиперболического усеченная пятиугольная мозаика порядка 4, t {5,4} с усеченным пятиугольником и квадратными гранями:

Связанные соты

Четыре усеченных обычных компактных соты в H³
Изображение
Символы	т {5,3,4}	т {4,3,5}	т {3,5,3}	т {5,3,5}
Вершина фигура

Додекаэдрические соты с усеченной структурой порядка 4

Додекаэдрические соты с усеченной структурой порядка 4 Bitruncated порядка-5 кубических сот
Тип	Равномерные соты в гиперболическом пространстве
Символ Шлефли	2т {5,3,4} 2т {5,3^1,1}
Диаграмма Кокстера	↔
Клетки	т {3,5} т {3,4}
Лица	квадрат {4} пятиугольник {5} шестиугольник {6}
Фигура вершины	дигональный дисфеноид
Группа Кокстера	${displaystyle {overline {BH}} _ {3}}$ , [4,3,5] ${displaystyle {overline {DH}} _ {3}}$ , [5,3^1,1]
Характеристики	Вершинно-транзитивный

В усеченная по битам додекаэдрическая сотовая структура порядка 4, или же bitruncated порядка-5 кубических сот, , имеет усеченный октаэдр и усеченный икосаэдр ячейки, с дигональный дисфеноид вершина фигуры.

Связанные соты

Три усеченных компактной соты в H³
Изображение
Символы	2т {4,3,5}	2т {3,5,3}	2т {5,3,5}
Вершина фигура

Додекаэдрические соты с кантеллированным порядком 4

Додекаэдрические соты с кантом четвертого порядка
Тип	Равномерные соты в гиперболическом пространстве
Символ Шлефли	рр {5,3,4} рр {5,3^1,1}
Диаграмма Кокстера	↔
Клетки	р-р {3,5} г {3,4} {} x {4}
Лица	треугольник {3} квадрат {4} пятиугольник {5}
Фигура вершины	клин
Группа Кокстера	${displaystyle {overline {BH}} _ {3}}$ , [4,3,5] ${displaystyle {overline {DH}} _ {3}}$ , [5,3^1,1]
Характеристики	Вершинно-транзитивный

В скошенные додекаэдрические соты порядка 4, , имеет ромбикосододекаэдр, кубооктаэдр, и куб ячейки, с клин вершина фигуры.

Связанные соты

Четыре скошенных регулярных компактных сот в H³

Изображение
Символы	рр {5,3,4}	рр {4,3,5}	рр {3,5,3}	рр {5,3,5}
Вершина фигура

Cantitruncated порядок-4 додекаэдрические соты

Cantitruncated порядок-4 додекаэдрические соты
Тип	Равномерные соты в гиперболическом пространстве
Символ Шлефли	tr {5,3,4} tr {5,3^1,1}
Диаграмма Кокстера	↔
Клетки	tr {3,5} т {3,4} {} x {4}
Лица	квадрат {4} шестиугольник {6} десятиугольник {10}
Фигура вершины	зеркальная клиновидная кость
Группа Кокстера	${displaystyle {overline {BH}} _ {3}}$ , [4,3,5] ${displaystyle {overline {DH}} _ {3}}$ , [5,3^1,1]
Характеристики	Вершинно-транзитивный

В усеченные додекаэдрические соты порядка 4, , имеет усеченный икосододекаэдр, усеченный октаэдр, и куб ячейки, с зеркальная клиновидная кость вершина фигуры.

Связанные соты

Четыре усеченных обычных компактных сот в H³
Изображение
Символы	tr {5,3,4}	tr {4,3,5}	tr {3,5,3}	тр {5,3,5}
Вершина фигура

Додекаэдрические соты Runcinated порядка 4

В додекаэдрические соты типа runcinated-4 такой же, как runcinated order-5 кубические соты.

Усеченная додекаэдрическая сотовая структура порядка 4

Усеченная додекаэдрическая сотовая структура порядка 4
Тип	Равномерные соты в гиперболическом пространстве
Символ Шлефли	т_0,1,3{5,3,4}
Диаграмма Кокстера
Клетки	т {5,3} рр {3,4} {} x {10} {} x {4}
Лица	треугольник {3} квадрат {4} десятиугольник {10}
Фигура вершины	равнобедренно-трапециевидный пирамида
Группа Кокстера	${displaystyle {overline {BH}} _ {3}}$ , [4,3,5]
Характеристики	Вершинно-транзитивный