Икосаэдрические соты - Icosahedral honeycomb
| Икосаэдрические соты | |
|---|---|
 Модель диска Пуанкаре | |
| Тип | Гиперболические обычные соты Равномерные гиперболические соты |
| Символ Шлефли | {3,5,3} |
| Диаграмма Кокстера | |
| Клетки | {3,5} |
| Лица | треугольник {3} |
| Край фигура | треугольник {3} |
| Фигура вершины | 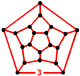 додекаэдр |
| Двойной | Самодвойственный |
| Группа Кокстера | , [3,5,3] |
| Характеристики | Обычный |
В икосаэдрические соты является одним из четырех компактных регулярных пространств, заполняющих мозаика (или же соты ) в гиперболическое 3-пространство. С Символ Шлефли {3,5,3}, всего три икосаэдры вокруг каждого ребра и 12 икосаэдров вокруг каждой вершины в правильном додекаэдр вершина фигуры.
А геометрические соты это заполнение пространства из многогранник или многомерный клетки, чтобы не было зазоров. Это пример более общего математического черепица или же мозаика в любом количестве измерений.
Соты обычно строятся из обычных Евклидово ("плоское") пространство, как и выпуклые однородные соты. Они также могут быть построены в неевклидовы пространства, Такие как гиперболические однородные соты. Любой конечный равномерный многогранник можно спроецировать на его окружающая сфера образовывать однородные соты в сферическом пространстве.
Описание
В двугранный угол из правильный икосаэдр составляет около 138,2 °, поэтому невозможно уместить три икосаэдра вокруг ребра в трехмерном евклидовом пространстве. Однако в гиперболическом пространстве икосаэдры с правильным масштабированием могут иметь двугранные углы ровно 120 градусов, поэтому три из них могут умещаться вокруг ребра.

Связанные обычные соты
В трехмерном гиперболическом пространстве есть четыре регулярных компактных соты:
 {5,3,4} |  {4,3,5} |  {3,5,3} |  {5,3,5} |
Связанные регулярные многогранники и соты
Это член последовательности регулярная полихора и соты {3,п, 3} с дельтраэдрический клетки:
| {3,п, 3} многогранники | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Космос | S3 | ЧАС3 | |||||||||
| Форма | Конечный | Компактный | Паракомпакт | Некомпактный | |||||||
| {3,п,3} | {3,3,3} | {3,4,3} | {3,5,3} | {3,6,3} | {3,7,3} | {3,8,3} | ... {3,∞,3} | ||||
| Изображение |  |  |  |  |  |  |  | ||||
| Клетки |  {3,3} |  {3,4} |  {3,5} |  {3,6} |  {3,7} |  {3,8} |  {3,∞} | ||||
| Вершина фигура |  {3,3} |  {4,3} |  {5,3} |  {6,3} |  {7,3} |  {8,3} |  {∞,3} | ||||
Он также является членом последовательности регулярная полихора и соты {п,5,п}, с фигуры вершин состоит из пятиугольников:
| {п,5,п} обычные соты | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Космос | ЧАС3 | ||||||||||
| Форма | Паракомпакт | Некомпактный | |||||||||
| Имя | {3,5,3} | {4,5,4} | {5,5,5} | {6,5,6} | {7,5,7} | {8,5,8} | ...{∞,5,∞} | ||||
| Изображение |  |  |  |  |  | ||||||
| Клетки {п,5} |  {3,5} |  {4,5} |  {5,5} |  {6,5} |  {7,5} |  {8,5} |  {∞,5} | ||||
| Вершина фигура {5,п} |  {5,3} |  {5,4} |  {5,5} |  {5,6} |  {5,7} |  {5,8} |  {5,∞} | ||||
Равномерные соты
Есть девять однородных сот в [3,5,3] Группа Кокстера семья, включая эту обычную форму, а также усеченный битами форма, т1,2{3,5,3}, ![]()
![]()
![]()
![]()
![]()
![]()
![]() , также называемый усеченные додекаэдрические соты, каждая из ячеек которого усеченные додекаэдры.
, также называемый усеченные додекаэдрические соты, каждая из ячеек которого усеченные додекаэдры.
| {3,5,3} | т1{3,5,3} | т0,1{3,5,3} | т0,2{3,5,3} | т0,3{3,5,3} |
|---|---|---|---|---|
 |  |  |  |  |
| т1,2{3,5,3} | т0,1,2{3,5,3} | т0,1,3{3,5,3} | т0,1,2,3{3,5,3} | |
 |  |  |  |
Ректифицированные икосаэдрические соты
| Ректифицированные икосаэдрические соты | |
|---|---|
| Тип | Равномерные соты в гиперболическом пространстве |
| Символ Шлефли | r {3,5,3} или t1{3,5,3} |
| Диаграмма Кокстера | |
| Клетки | г {3,5} {5,3} |
| Лица | треугольник {3} пятиугольник {5} |
| Фигура вершины | 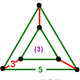 треугольная призма |
| Группа Кокстера | , [3,5,3] |
| Характеристики | Вершинно-транзитивный, реберный транзитивный |
В ректифицированные икосаэдрические соты, т1{3,5,3}, ![]()
![]()
![]()
![]()
![]()
![]()
![]() , имеет чередующиеся додекаэдр и икосододекаэдр ячейки, с треугольная призма фигура вершины:
, имеет чередующиеся додекаэдр и икосододекаэдр ячейки, с треугольная призма фигура вершины:


Перспективные прогнозы из центра Модель диска Пуанкаре
Связанные соты
Всего существует четыре выпрямленных компактных обычных соты:
| Изображение |  |  |  |  |
|---|---|---|---|---|
| Символы | г {5,3,4} | г {4,3,5} | г {3,5,3} | г {5,3,5} |
| Вершина фигура |  |  |  |  |
Усеченные икосаэдрические соты
| Усеченные икосаэдрические соты | |
|---|---|
| Тип | Равномерные соты в гиперболическом пространстве |
| Символ Шлефли | т {3,5,3} или т0,1{3,5,3} |
| Диаграмма Кокстера | |
| Клетки | т {3,5} {5,3} |
| Лица | пятиугольник {5} шестиугольник {6} |
| Фигура вершины | 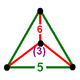 треугольная пирамида |
| Группа Кокстера | , [3,5,3] |
| Характеристики | Вершинно-транзитивный |
В усеченные икосаэдрические соты, т0,1{3,5,3}, ![]()
![]()
![]()
![]()
![]()
![]()
![]() , имеет чередующиеся додекаэдр и усеченный икосаэдр ячейки, с треугольная пирамида фигура вершины.
, имеет чередующиеся додекаэдр и усеченный икосаэдр ячейки, с треугольная пирамида фигура вершины.

Связанные соты
| Изображение |  |  |  |  |
|---|---|---|---|---|
| Символы | т {5,3,4} | т {4,3,5} | т {3,5,3} | т {5,3,5} |
| Вершина фигура |  |  |  |  |
Усеченные икосаэдрические соты
| Усеченные икосаэдрические соты | |
|---|---|
| Тип | Равномерные соты в гиперболическом пространстве |
| Символ Шлефли | 2т {3,5,3} или т1,2{3,5,3} |
| Диаграмма Кокстера | |
| Клетки | т {5,3} |
| Лица | треугольник {3} десятиугольник {10} |
| Фигура вершины | 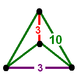 тетрагональный дисфеноид |
| Группа Кокстера | , [[3,5,3]] |
| Характеристики | Вершинно-транзитивный, реберный, клеточно-транзитивный |
В усеченные икосаэдрические соты, т1,2{3,5,3}, ![]()
![]()
![]()
![]()
![]()
![]()
![]() , имеет усеченный додекаэдр ячейки с тетрагональный дисфеноид фигура вершины.
, имеет усеченный додекаэдр ячейки с тетрагональный дисфеноид фигура вершины.

Связанные соты
| Изображение |  |  |  |
|---|---|---|---|
| Символы | 2т {4,3,5} | 2т {3,5,3} | 2т {5,3,5} |
| Вершина фигура |  |  |  |
Скошенные икосаэдрические соты
| Скошенные икосаэдрические соты | |
|---|---|
| Тип | Равномерные соты в гиперболическом пространстве |
| Символ Шлефли | rr {3,5,3} или t0,2{3,5,3} |
| Диаграмма Кокстера | |
| Клетки | р-р {3,5} г {5,3} {} x {3} |
| Лица | треугольник {3} квадрат {4} пятиугольник {5} |
| Фигура вершины | 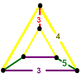 клин |
| Группа Кокстера | , [3,5,3] |
| Характеристики | Вершинно-транзитивный |
В скошенные икосаэдрические соты, т0,2{3,5,3}, ![]()
![]()
![]()
![]()
![]()
![]()
![]() , имеет ромбикосододекаэдр, икосододекаэдр, и треугольная призма ячейки, с клин фигура вершины.
, имеет ромбикосододекаэдр, икосододекаэдр, и треугольная призма ячейки, с клин фигура вершины.

Связанные соты
| Четыре скошенных регулярных компактных сот в H3 | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
Сота с усеченным икосаэдром
| Сота с усеченным икосаэдром | |
|---|---|
| Тип | Равномерные соты в гиперболическом пространстве |
| Символ Шлефли | tr {3,5,3} или t0,1,2{3,5,3} |
| Диаграмма Кокстера | |
| Клетки | tr {3,5} т {5,3} {} x {3} |
| Лица | треугольник {3} квадрат {4} шестиугольник {6} десятиугольник {10} |
| Фигура вершины | 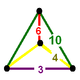 зеркальная клиновидная кость |
| Группа Кокстера | , [3,5,3] |
| Характеристики | Вершинно-транзитивный |
В усеченные икосаэдрические соты, т0,1,2{3,5,3}, ![]()
![]()
![]()
![]()
![]()
![]()
![]() , имеет усеченный икосододекаэдр, усеченный додекаэдр, и треугольная призма ячейки, с зеркальная клиновидная кость вершина фигуры.
, имеет усеченный икосододекаэдр, усеченный додекаэдр, и треугольная призма ячейки, с зеркальная клиновидная кость вершина фигуры.

Связанные соты
| Изображение |  |  |  |  |
|---|---|---|---|---|
| Символы | tr {5,3,4} | tr {4,3,5} | tr {3,5,3} | тр {5,3,5} |
| Вершина фигура |  |  |  |  |
Ячеистые икосаэдрические соты
| Ячеистые икосаэдрические соты | |
|---|---|
| Тип | Равномерные соты в гиперболическом пространстве |
| Символ Шлефли | т0,3{3,5,3} |
| Диаграмма Кокстера | |
| Клетки | {3,5} {}×{3} |
| Лица | треугольник {3} квадрат {4} |
| Фигура вершины | 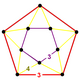 пятиугольная антипризма |
| Группа Кокстера | , [[3,5,3]] |
| Характеристики | Вершинно-транзитивный, реберный транзитивный |
В ячеистые икосаэдрические соты, т0,3{3,5,3}, ![]()
![]()
![]()
![]()
![]()
![]()
![]() , имеет икосаэдр и треугольная призма ячейки, с пятиугольная антипризма фигура вершины.
, имеет икосаэдр и треугольная призма ячейки, с пятиугольная антипризма фигура вершины.

- Вид из центра треугольной призмы
Связанные соты
| Изображение |  |  |  |
|---|---|---|---|
| Символы | т0,3{4,3,5} | т0,3{3,5,3} | т0,3{5,3,5} |
| Вершина фигура |  |  |  |
Усеченные икосаэдрические соты
| Усеченные икосаэдрические соты | |
|---|---|
| Тип | Равномерные соты в гиперболическом пространстве |
| Символ Шлефли | т0,1,3{3,5,3} |
| Диаграмма Кокстера | |
| Клетки | т {3,5} р-р {3,5} {}×{3} {}×{6} |
| Лица | треугольник {3} квадрат {4} пятиугольник {5} шестиугольник {6} |
| Фигура вершины | 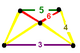 равнобедренно-трапециевидный пирамида |
| Группа Кокстера | , [3,5,3] |
| Характеристики | Вершинно-транзитивный |
В усеченные икосаэдрические соты, т0,1,3{3,5,3}, ![]()
![]()
![]()
![]()
![]()
![]()
![]() , имеет усеченный икосаэдр, ромбикосододекаэдр, шестиугольная призма, и треугольная призма ячейки, с равнобедренно-трапециевидный пирамида вершина фигуры.
, имеет усеченный икосаэдр, ромбикосододекаэдр, шестиугольная призма, и треугольная призма ячейки, с равнобедренно-трапециевидный пирамида вершина фигуры.
В соты с гантелями эквивалентно усеченным икосаэдрическим сотам.

- Вид из центра треугольной призмы
Связанные соты
| Четыре ряда усеченных обычных компактных сот в H3 | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
Усеченные икосаэдрические соты
| Усеченные икосаэдрические соты | |
|---|---|
| Тип | Равномерные соты в гиперболическом пространстве |
| Символ Шлефли | т0,1,2,3{3,5,3} |
| Диаграмма Кокстера | |
| Клетки | tr {3,5} {}×{6} |
| Лица | квадрат {4} шестиугольник {6} двенадцатигранник {10} |
| Фигура вершины |  филлический дисфеноид |
| Группа Кокстера | , [[3,5,3]] |
| Характеристики | Вершинно-транзитивный |
В усеченные икосаэдрические соты, т0,1,2,3{3,5,3}, ![]()
![]()
![]()
![]()
![]()
![]()
![]() , имеет усеченный икосододекаэдр и шестиугольная призма ячейки, с филлический дисфеноид фигура вершины.
, имеет усеченный икосододекаэдр и шестиугольная призма ячейки, с филлический дисфеноид фигура вершины.

- По центру шестиугольной призмы
Связанные соты
| Три полностью усеченных обычных компактных соты в H3 | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
Омниснуб икосаэдрические соты
| Омниснуб икосаэдрические соты | |
|---|---|
| Тип | Равномерные соты в гиперболическом пространстве |
| Символ Шлефли | ч (т0,1,2,3{3,5,3}) |
| Диаграмма Кокстера | |
| Клетки | ср {3,5} с {2,3} irr. {3,3} |
| Лица | треугольник {3} пятиугольник {5} |
| Фигура вершины |  |
| Группа Кокстера | [[3,5,3]]+ |
| Характеристики | Вершинно-транзитивный |
В омниснуб икосаэдрические соты, ч (т0,1,2,3{3,5,3}), ![]()
![]()
![]()
![]()
![]()
![]()
![]() , имеет курносый додекаэдр, октаэдр, и тетраэдр ячеек, с неправильной фигурой вершины. это вершинно-транзитивный, но нельзя сделать с однородными ячейками.
, имеет курносый додекаэдр, октаэдр, и тетраэдр ячеек, с неправильной фигурой вершины. это вершинно-транзитивный, но нельзя сделать с однородными ячейками.
Частично уменьшенные икосаэдрические соты
| Частично уменьшенные икосаэдрические соты Икосаэдрические соты с парабидуменьшением | |
|---|---|
| Тип | Равномерные соты |
| Символ Шлефли | pd {3,5,3} |
| Диаграмма Кокстера | - |
| Клетки | {5,3} с {2,5} |
| Лица | треугольник {3} пятиугольник {5} |
| Фигура вершины |  тетраэдрически уменьшенный додекаэдр |
| Группа Кокстера | 1/5[3,5,3]+ |
| Характеристики | Вершинно-транзитивный |
В частично уменьшенные икосаэдрические соты или же парабидуменьшенный икосаэдр соты, pd {3,5,3}, - однородные соты, не относящиеся к Витоффу с додекаэдр и пятиугольная антипризма ячейки, с тетраэдрически уменьшенный додекаэдр фигура вершины. Ячейки икосаэдра {3,5,3} являются уменьшился в противоположных вершинах (парабидимулирует), оставляя пятиугольная антипризма (парабидоусиленный икосаэдр ) core и создание новых ячеек додекаэдра сверху и снизу.[1][2]


Смотрите также
- Выпуклые однородные соты в гиперболическом пространстве
- Регулярные мозаики гиперболического 3-мерного пространства
- Пространство Зейферта – Вебера
- 11-элементный - An абстрактный регулярный полихорон который разделяет {3,5,3} Символ Шлефли.
Рекомендации
- ^ Венди Ю. Кригер, Стены и мосты: вид из шести измерений, Симметрия: культура и наука Том 16, номер 2, страницы 171–192 (2005) [1] В архиве 2013-10-07 в Wayback Machine
- ^ http://www.bendwavy.org/klitzing/incmats/pt353.htm
- Coxeter, Правильные многогранники, 3-й. изд., Dover Publications, 1973. ISBN 0-486-61480-8. (Таблицы I и II: Правильные многогранники и соты, стр. 294–296)
- Coxeter, Красота геометрии: двенадцать эссе, Dover Publications, 1999 г. ISBN 0-486-40919-8 (Глава 10: Обычные соты в гиперболическом пространстве, Сводные таблицы II, III, IV, V, стр. 212-213)
- Норман Джонсон Равномерные многогранники, Рукопись
- N.W. Джонсон: Теория однородных многогранников и сот, Кандидат наук. Диссертация, Университет Торонто, 1966 г.
- N.W. Джонсон: Геометрии и преобразования, (2018) Глава 13: Гиперболические группы Кокстера
- Клитцинг, Ричард. "Гиперболические соты H3 гиперболическая мозаика икосаэдра 3-го порядка".


























