Равномерные соты в гиперболическом пространстве - Uniform honeycombs in hyperbolic space

В гиперболическая геометрия, а однородные соты в гиперболическом пространстве это униформа мозаика из равномерный многогранник клетки. В 3-х мерном гиперболическое пространство есть девять Группа Коксетера семей компактных выпуклые однородные соты, сгенерированный как Конструкции Wythoff, и представлен перестановки из кольца из Диаграммы Кокстера для каждой семьи.

Нерешенная проблема в математике: Найдите полный набор гиперболических однородных сот (больше нерешенных задач по математике)

Четыре компактных обычных гиперболических соты

{5,3,4}	{5,3,5}
{4,3,5}	{3,5,3}
Модель шара Пуанкаре прогнозы

Гиперболические однородные сотовые семейства

Соты делятся на компактные и паракомпактные формы, определяемые Группы Кокстера, первая категория включает только конечные клетки и фигуры вершин (конечные подгруппы), а вторая включает аффинные подгруппы.

Компактные однородные сотовые семейства

Девять компактных Группы Кокстера перечислены здесь с их Диаграммы Кокстера,^[1] в порядке относительных объемов их фундаментальные симплексные области.^[2]

Эти 9 семейств создают в общей сложности 76 уникальных однородных сот. Полный список гиперболических однородных сот не доказан, и существует неизвестное количество неитхоффовских форм. Один известный пример приводится ниже с семейством {3,5,3}. Только два семейства связаны как половинка удаления зеркала: [5,3^1,1] ↔ [5,3,4,1⁺].

Проиндексировано	Фундаментальный симплекс объем[3]	Витт символ	Coxeter обозначение	Коммутатор подгруппа	Coxeter диаграмма	Соты
ЧАС1	0.0358850633	${displaystyle {ar {BH}}_{3}}$	[5,3,4]	[(5,3)^+,4,1^+] = [5,3^1,1]^+		15 форм, 2 обычных
ЧАС2	0.0390502856	${displaystyle {ar {J}}_{3}}$	[3,5,3]	[3,5,3]^+		9 форм, 1 обычная
ЧАС3	0.0717701267	${displaystyle {ar {DH}}_{3}}$	[5,3^1,1]	[5,3^1,1]^+		11 форм (7 совпадают с семейством [5,3,4], 4 уникальны)
ЧАС4	0.0857701820	${displaystyle {widehat {AB}}_{3}}$	[(4,3,3,3)]	[(4,3,3,3)]^+		9 форм
ЧАС5	0.0933255395	${displaystyle {ar {K}}_{3}}$	[5,3,5]	[5,3,5]^+		9 форм, 1 обычная
ЧАС6	0.2052887885	${displaystyle {widehat {AH}}_{3}}$	[(5,3,3,3)]	[(5,3,3,3)]^+		9 форм
ЧАС7	0.2222287320	${displaystyle {widehat {BB}}_{3}}$	[(4,3)^[2]]	[(4,3^+,4,3^+)]		6 форм
ЧАС8	0.3586534401	${displaystyle {widehat {BH}}_{3}}$	[(3,4,3,5)]	[(3,4,3,5)]^+		9 форм
ЧАС9	0.5021308905	${displaystyle {widehat {HH}}_{3}}$	[(5,3)^[2]]	[(5,3)^[2]]^+		6 форм

Есть только две радикальные подгруппы с несимплектическими доменами, которые могут быть созданы путем удаления набора из двух или более зеркал, разделенных всеми другими зеркалами ветвями четного порядка. Один - [(4,3,4,3^*)], представленные диаграммами Кокстера подгруппа индекса 6 с треугольный трапецоэдр фундаментальная область ↔ , который можно расширить, восстановив одно зеркало как . Другой - [4, (3,5)^*], индекс 120 с додекаэдр фундаментальный домен.

Паракомпактные гиперболические однородные соты

Дальнейшая информация: паракомпактные однородные соты

Также есть 23 паракомпактные группы Кокстера ранга 4, которые производят паракомпактные однородные соты с бесконечным или неограниченным грани или же вершина фигуры, включая идеальные вершины на бесконечности.

Резюме гиперболической паракомпактной группы

Тип	Группы Кокстера
Линейные графики	| | | | | |
Трайдентальные графики	| |
Циклические графы	| | | | | | | |
Графы петли и хвоста	| | |

Другие паракомпактные группы Кокстера существуют как Многогранник Винберга фундаментальные области, включая эти треугольная бипирамида фундаментальные области (двойные тетраэдры) как графы ранга 5, включая параллельные зеркала. Равномерные соты существуют как все перестановки колец в этих графах с ограничением, что хотя бы один узел должен быть окружен через ветви бесконечного порядка.

Измерение	Классифицировать	Графики
ЧАС^3	5	, , , , , , , , , , , , , , , , , , , , , , , , , , ,

[3,5,3] семья

Есть 9 форм, порожденных перестановками колец Группа Коксетера: [3,5,3] или

Один связанный не вайтхоффианец форма построена из фигуры вершины {3,5,3} с удаленными 4 (тетраэдрически расположенными) вершинами, создавая пятиугольные антипризмы и додекаэдры, заполняющие промежутки, называемые тетраэдрически уменьшенный додекаэдр.^[4]

Усеченная и усеченная формы (5 и 6) содержат грани двух правильные косые многогранники: {4,10 | 3} и {10,4 | 3}.

#	Имя соты Диаграмма Кокстера и Schläfli символы	Количество ячеек / вершина и позиции в сотах				Фигура вершины	Рисунок
		0	1	2	3
1	икосаэдр т0{3,5,3}				(12) (3.3.3.3.3)
2	выпрямленный икосаэдр т1{3,5,3}	(2) (5.5.5)			(3) (3.5.3.5)
3	усеченный икосаэдр т0,1{3,5,3}	(1) (5.5.5)			(3) (5.6.6)
4	скошенный икосаэдр т0,2{3,5,3}	(1) (3.5.3.5)	(2) (4.4.3)		(2) (3.5.4.5)
5	беглый икосаэдр т0,3{3,5,3}	(1) (3.3.3.3.3)	(5) (4.4.3)	(5) (4.4.3)	(1) (3.3.3.3.3)
6	усеченный икосаэдр т1,2{3,5,3}	(2) (3.10.10)			(2) (3.10.10)
7	усеченный икосаэдр т0,1,2{3,5,3}	(1) (3.10.10)	(1) (4.4.3)		(2) (4.6.10)
8	усеченный икосаэдр т0,1,3{3,5,3}	(1) (3.5.4.5)	(1) (4.4.3)	(2) (4.4.6)	(1) (5.6.6)
9	усеченный икосаэдр т0,1,2,3{3,5,3}	(1) (4.6.10)	(1) (4.4.6)	(1) (4.4.6)	(1) (4.6.10)

#	Имя соты Диаграмма Кокстера и Schläfli символы	Количество ячеек / вершина и позиции в сотах					Фигура вершины	Рисунок
		0	1	2	3	Alt
[77]	частично уменьшенный икосаэдр pd {3,5,3}[5]				(12) (3.3.3.5)	(4) (5.5.5)
Неоднородный	омниснуб икосаэдр ht0,1,2,3{3,5,3}	(1) (3.3.3.3.5)	(1) (3.3.3.3	(1) (3.3.3.3)	(1) (3.3.3.3.5)	(4) +(3.3.3)

[5,3,4] семья

Существует 15 форм, порожденных перестановками колец Группа Коксетера: [5,3,4] или .

Это семейство относится к группе [5,3^1,1] полусимметрией [5,3,4,1⁺], или же ↔ , когда последнее зеркало после ветви порядка 4 неактивно, или как чередование, если неактивно третье зеркало ↔ .

#	Название соты Диаграмма Кокстера	Ячейки по местоположению и количеству на вершину				Фигура вершины	Рисунок
		0	1	2	3
10	додекаэдрический порядок 4 ↔	-	-	-	(8) (5.5.5)
11	выпрямленный додекаэдр порядка 4 ↔	(2) (3.3.3.3)	-	-	(4) (3.5.3.5)
12	выпрямленный заказ-5 куб. ↔	(5) (3.4.3.4)	-	-	(2) (3.3.3.3.3)
13	порядка-5 куб.	(20) (4.4.4)	-	-	-
14	усеченный додекаэдр четвертого порядка ↔	(1) (3.3.3.3)	-	-	(4) (3.10.10)
15	bitruncated порядка 5 кубических ↔	(2) (4.6.6)	-	-	(2) (5.6.6)
16	усеченный порядок-5 куб.	(5) (3.8.8)	-	-	(1) (3.3.3.3.3)
17	скошенный додекаэдр четвертого порядка ↔	(1) (3.4.3.4)	(2) (4.4.4)	-	(2) (3.4.5.4)
18	скошенный порядок-5 куб.	(2) (3.4.4.4)	-	(2) (4.4.5)	(1) (3.5.3.5)
19	запущенный заказ-5 куб.	(1) (4.4.4)	(3) (4.4.4)	(3) (4.4.5)	(1) (5.5.5)
20	усеченный додекаэдр четвертого порядка ↔	(1) (4.6.6)	(1) (4.4.4)	-	(2) (4.6.10)
21	усеченный порядок-5 куб.	(2) (4.6.8)	-	(1) (4.4.5)	(1) (5.6.6)
22	усеченный додекаэдр порядка 4	(1) (3.4.4.4)	(1) (4.4.4)	(2) (4.4.10)	(1) (3.10.10)
23	runcitruncated order-5 кубический	(1) (3.8.8)	(2) (4.4.8)	(1) (4.4.5)	(1) (3.4.5.4)
24	омниусеченный порядок-5 куб.	(1) (4.6.8)	(1) (4.4.8)	(1) (4.4.10)	(1) (4.6.10)

#	Название соты Диаграмма Кокстера	Ячейки по местоположению и количеству на вершину					Фигура вершины	Рисунок
		0	1	2	3	Alt
[34]	чередование порядка-5 куб. ↔	(20) (3.3.3)			(12) (3.3.3.3.3)
[35]	кантик орден-5 куб. ↔	(1) (3.5.3.5)	-	(2) (5.6.6)	(2) (3.6.6)
[36]	рунский порядок-5 куб. ↔	(1) (5.5.5)	-	(3) (3.4.5.4)	(1) (3.3.3)
[37]	рунический орден-5 куб. ↔	(1) (3.10.10)	-	(2) (4.6.10)	(1) (3.6.6)
Неоднородный	курносый выпрямленный додекаэдр порядка 4	(1) (3.3.3.3.3)	(1) (3.3.3)	-	(2) (3.3.3.3.5)	(4) +(3.3.3)	Irr. трехуменьшенный икосаэдр
Неоднородный	Рунчик курносый выпрямленный порядок-4 додекаэдр	(3.4.4.4)	(4.4.4.4)	-	(3.3.3.3.5)	+(3.3.3)
Неоднородный	омниснуб заказ-5 куб.	(1) (3.3.3.3.4)	(1) (3.3.3.4)	(1) (3.3.3.5)	(1) (3.3.3.3.5)	(4) +(3.3.3)

[5,3,5] семья

Есть 9 форм, порожденных кольцевыми перестановками Группа Коксетера: [5,3,5] или

Обрезанные и обработанные формы (29 и 30) содержат лица двух правильные косые многогранники: {4,6 | 5} и {6,4 | 5}.

#	Название соты Диаграмма Кокстера	Ячейки по местоположению и количеству на вершину				Фигура вершины	Рисунок
		0	1	2	3
25	(Обычный) Орден-5 додекаэдр т0{5,3,5}				(20) (5.5.5)
26	выпрямленный додекаэдр порядка 5 т1{5,3,5}	(2) (3.3.3.3.3)			(5) (3.5.3.5)
27	усеченный додекаэдр порядка 5 т0,1{5,3,5}	(1) (3.3.3.3.3)			(5) (3.10.10)
28	скошенный додекаэдр порядка 5 т0,2{5,3,5}	(1) (3.5.3.5)	(2) (4.4.5)		(2) (3.5.4.5)
29	Управляемый додекаэдром порядка 5 т0,3{5,3,5}	(1) (5.5.5)	(3) (4.4.5)	(3) (4.4.5)	(1) (5.5.5)
30	усеченный по битам додекаэдр порядка 5 т1,2{5,3,5}	(2) (5.6.6)			(2) (5.6.6)
31	усеченный додекаэдр порядка 5 т0,1,2{5,3,5}	(1) (5.6.6)	(1) (4.4.5)		(2) (4.6.10)
32	усеченный додекаэдр порядка 5 т0,1,3{5,3,5}	(1) (3.5.4.5)	(1) (4.4.5)	(2) (4.4.10)	(1) (3.10.10)
33	всенаправленный додекаэдр пятого порядка т0,1,2,3{5,3,5}	(1) (4.6.10)	(1) (4.4.10)	(1) (4.4.10)	(1) (4.6.10)

#	Название соты Диаграмма Кокстера	Ячейки по местоположению и количеству на вершину					Фигура вершины	Рисунок
		0	1	2	3	Alt
Неоднородный	омниснуб порядок-5 додекаэдр ht0,1,2,3{5,3,5}	(1) (3.3.3.3.5)	(1) (3.3.3.5)	(1) (3.3.3.5)	(1) (3.3.3.3.5)	(4) +(3.3.3)

[5,3^1,1] семья

Имеется 11 форм (и только 4 не являются общими с семейством [5,3,4]), порожденных перестановками колец Группа Коксетера: [5,3^1,1] или же . Если состояния ветвящихся колец совпадают, расширенная симметрия может удвоиться в семейство [5,3,4], ↔ .

#	Имя соты Диаграмма Кокстера	Ячейки по местоположению (и считайте вокруг каждой вершины)				вершина фигуры	Рисунок
		0	1	0'	3
34	чередование порядка-5 куб. ↔	-	-	(12) (3.3.3.3.3)	(20) (3.3.3)
35	кантик орден-5 куб. ↔	(1) (3.5.3.5)	-	(2) (5.6.6)	(2) (3.6.6)
36	рунский порядок-5 куб. ↔	(1) (5.5.5)	-	(3) (3.4.5.4)	(1) (3.3.3)
37	рунический орден-5 куб. ↔	(1) (3.10.10)	-	(2) (4.6.10)	(1) (3.6.6)

#	Имя соты Диаграмма Кокстера ↔	Ячейки по местоположению (и считайте вокруг каждой вершины)				вершина фигуры	Рисунок
		0	1	3	Alt
[10]	Орден-4 додекаэдр ↔	(4) (5.5.5)	-	-
[11]	выпрямленный додекаэдр порядка 4 ↔	(2) (3.5.3.5)	-	(2) (3.3.3.3)
[12]	выпрямленный заказ-5 куб. ↔	(1) (3.3.3.3.3)	-	(5) (3.4.3.4)
[15]	bitruncated порядка 5 кубических ↔	(1) (5.6.6)	-	(2) (4.6.6)
[14]	усеченный додекаэдр четвертого порядка ↔	(2) (3.10.10)	-	(1) (3.3.3.3)
[17]	скошенный додекаэдр четвертого порядка ↔	(1) (3.4.5.4)	(2) (4.4.4)	(1) (3.4.3.4)
[20]	усеченный додекаэдр четвертого порядка ↔	(1) (4.6.10)	(1) (4.4.4)	(1) (4.6.6)
Неоднородный	курносый выпрямленный додекаэдр порядка 4 ↔	(2) (3.3.3.3.5)	(1) (3.3.3)	(2) (3.3.3.3.3)	(4) +(3.3.3)	Irr. трехуменьшенный икосаэдр

[(4,3,3,3)] семья

Есть 9 форм, порожденных кольцевыми перестановками Группа Коксетера:

Обрезанные и обработанные формы (41 и 42) содержат грани двух правильные косые многогранники: {8,6 | 3} и {6,8 | 3}.

#	Имя соты Диаграмма Кокстера	Ячейки по местоположению (и считайте вокруг каждой вершины)					вершина фигуры	Рисунок
		0	1	2	3	Alt
38	тетраэдрический кубический {(3,3,3,4)}	(4) (3.3.3)	-	(4) (4.4.4)	(6) (3.4.3.4)
39	тетраэдрический-октаэдрический {(3,3,4,3)}	(12) (3.3.3.3)	(8) (3.3.3)	-	(8) (3.3.3.3)
40	циклоусеченный тетраэдрический кубический ct {(3,3,3,4)}	(3) (3.6.6)	(1) (3.3.3)	(1) (4.4.4)	(3) (4.6.6)
41	циклоусеченный куб-тетраэдр ct {(4,3,3,3)}	(1) (3.3.3)	(1) (3.3.3)	(3) (3.8.8)	(3) (3.8.8)
42	циклоусеченный тетраэдр-октаэдр ct {(3,3,4,3)}	(4) (3.6.6)	(4) (3.6.6)	(1) (3.3.3.3)	(1) (3.3.3.3)
43	выпрямленный тетраэдрический кубический г {(3,3,3,4)}	(1) (3.3.3.3)	(2) (3.4.3.4)	(1) (3.4.3.4)	(2) (3.4.4.4)
44	усеченный тетраэдрический кубический т {(3,3,3,4)}	(1) (3.6.6)	(1) (3.4.3.4)	(1) (3.8.8)	(2) (4.6.8)
45	усеченный тетраэдр-октаэдр т {(3,3,4,3)}	(2) (4.6.6)	(1) (3.6.6)	(1) (3.4.4.4)	(1) (4.6.6)
46	полностью усеченный тетраэдрический кубический tr {(3,3,3,4)}	(1) (4.6.6)	(1) (4.6.6)	(1) (4.6.8)	(1) (4.6.8)
Неоднородный	омниснуб четырехгранно-кубический sr {(3,3,3,4)}	(1) (3.3.3.3.3)	(1) (3.3.3.3.3)	(1) (3.3.3.3.4)	(1) (3.3.3.3.4)	(4) +(3.3.3)

[(5,3,3,3)] семья

Есть 9 форм, порожденных кольцевыми перестановками Группа Коксетера:

Обрезанные и обработанные формы (50 и 51) содержат грани двух правильные косые многогранники: {10,6 | 3} и {6,10 | 3}.

#	Имя соты Диаграмма Кокстера	Ячейки по местоположению (и посчитайте вокруг каждой вершины)				вершина фигуры	Рисунок
		0	1	2	3
47	четырехгранно-додекаэдрический	(4) (3.3.3)	-	(4) (5.5.5)	(6) (3.5.3.5)
48	четырехгранно-икосаэдрический	(30) (3.3.3.3)	(20) (3.3.3)	-	(12) (3.3.3.3.3)
49	циклоусеченный тетраэдр-додекаэдр	(3) (3.6.6)	(1) (3.3.3)	(1) (5.5.5)	(3) (5.6.6)
52	выпрямленный тетраэдр-додекаэдр	(1) (3.3.3.3)	(2) (3.4.3.4)	(1) (3.5.3.5)	(2) (3.4.5.4)
53	усеченный тетраэдр-додекаэдр	(1) (3.6.6)	(1) (3.4.3.4)	(1) (3.10.10)	(2) (4.6.10)
54	усеченный тетраэдр-икосаэдр	(2) (4.6.6)	(1) (3.6.6)	(1) (3.4.5.4)	(1) (5.6.6)

#	Имя соты Диаграмма Кокстера	Ячейки по местоположению (и посчитайте вокруг каждой вершины)			вершина фигуры	Рисунок
		0,1	2,3	Alt
50	циклоусеченный додекаэдр-тетраэдр	(2) (3.3.3)	(6) (3.10.10)
51	циклоусеченный тетраэдр-икосаэдр	(10) (3.6.6)	(2) (3.3.3.3.3)
55	усеченный тетраэдр-додекаэдр	(2) (4.6.6)	(2) (4.6.10)
Неоднородный	всенаправленный тетраэдр-додекаэдр	(2) (3.3.3.3.3)	(2) (3.3.3.3.5)	(4) +(3.3.3)

[(4,3,4,3)] семья

Есть 6 форм, порожденных перестановками колец Группа Коксетера: . Возможны 4 расширенные симметрии, основанные на симметрии колец: , , , и .

Это семейство симметрий также связано с радикальной подгруппой индекса 6, ↔ , построенный по [(4,3,4,3^*)], и представляет собой треугольный трапецоэдр фундаментальная область.

Усеченные формы (57 и 58) содержат грани двух правильные косые многогранники: {6,6 | 4} и {8,8 | 3}.

#	Имя соты Диаграмма Кокстера	Ячейки по местоположению (и считайте вокруг каждой вершины)				вершина фигуры	Картинки
		0	1	2	3
56	кубооктаэдрический	(6) (3.3.3.3)	-	(8) (4.4.4)	(12) (3.4.3.4)
60	усеченный кубооктаэдрический	(1) (4.6.6)	(1) (3.4.4.4)	(1) (3.8.8)	(2) (4.6.8)

#	Имя соты Диаграмма Кокстера	Ячейки по местоположению (и считайте вокруг каждой вершины)			вершина фигуры	Рисунок
		0,3	1,2	Alt
57	циклоусеченный октаэдрический кубический	(6) (4.6.6)	(2) (4.4.4)
Неоднородный	циклоснуб октаэдрический кубический	(4) (3.3.3.3.3)	(2) (3.3.3)	(4) +(3.3.3.3)

#	Имя соты Диаграмма Кокстера	Ячейки по местоположению (и считайте вокруг каждой вершины)		вершина фигуры	Рисунок
		0,1	2,3
58	циклоусеченный кубооктаэдрический	(2) (3.3.3.3)	(6) (3.8.8)

#	Имя соты Диаграмма Кокстера	Ячейки по местоположению (и посчитайте вокруг каждой вершины)		вершина фигуры	Рисунок
		0,2	1,3
59	ректификованный кубооктаэдрический	(2) (3.4.3.4)	(4) (3.4.4.4)

#	Имя соты Диаграмма Кокстера	Ячейки по местоположению (и считайте вокруг каждой вершины)		вершина фигуры	Рисунок
		0,1,2,3	Alt
61	всестороннеусеченный кубооктаэдрический	(4) (4.6.8)
Неоднородный	омниснуб кубо-восьмигранный	(4) (3.3.3.3.4)	(4) +(3.3.3)

[(4,3,5,3)] семья

Есть 9 форм, порожденных кольцевыми перестановками Группа Коксетера:

Усеченные формы (65 и 66) содержат грани двух правильные косые многогранники: {10,6 | 3} и {6,10 | 3}.

#	Имя соты Диаграмма Кокстера	Ячейки по местоположению (и считайте вокруг каждой вершины)				вершина фигуры	Рисунок
		0	1	2	3
62	октаэдр-додекаэдр	(6) (3.3.3.3)	-	(8) (5.5.5)	(1) (3.5.3.5)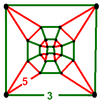
63	кубико-икосаэдрический	(30) (3.4.3.4)	(20) (4.4.4)	-	(12) (3.3.3.3.3)
64	цикло-усеченный октаэдрический-додекаэдрический	(3) (4.6.6)	(1) (4.4.4)	(1) (5.5.5)	(3) (5.6.6)
67	выпрямленный октаэдрический-додекаэдрический	(1) (3.4.3.4)	(2) (3.4.4.4)	(1) (3.5.3.5)	(2) (3.4.5.4)
68	усеченный октаэдр-додекаэдр	(1) (4.6.6)	(1) (3.4.4.4)	(1) (3.10.10)	(2) (4.6.10)
69	усеченный кубический додекаэдр	(2) (4.6.8)	(1) (3.8.8)	(1) (3.4.5.4)	(1) (5.6.6)

#	Имя соты Диаграмма Кокстера	Ячейки по местоположению (и считайте вокруг каждой вершины)			вершина фигуры	Рисунок
		0,1	2,3	Alt
65	циклоусеченный додекаэдр-октаэдр	(2) (3.3.3.3)	(8) (3.10.10)
66	циклоусеченный кубико-икосаэдр	(10) (3.8.8)	(2) (3.3.3.3.3)
70	всенаправленный октаэдрический додекаэдр	(2) (4.6.8)	(2) (4.6.10)
Неоднородный	всенаправленный октаэдр-додекаэдр	(2) (3.3.3.3.4)	(2) (3.3.3.3.5)	(4) +(3.3.3)

[(5,3,5,3)] семья

Есть 6 форм, порожденных перестановками колец Группа Коксетера: . Возможны 4 расширенные симметрии, основанные на симметрии колец: , , , и .

Усеченные формы (72 и 73) содержат грани двух правильные косые многогранники: {6,6 | 5} и {10,10 | 3}.

#	Имя соты Диаграмма Кокстера	Ячейки по местоположению (и считайте вокруг каждой вершины)					вершина фигуры	Рисунок
		0	1	2	3	Alt
71	додекаэдр-икосаэдр	(12) (3.3.3.3.3)	-	(20) (5.5.5)	(30) (3.5.3.5)
72	циклоусеченный икосаэдр-додекаэдр	(3) (5.6.6)	(1) (5.5.5)	(1) (5.5.5)	(3) (5.6.6)
73	циклоусеченный додекаэдр-икосаэдр	(1) (3.3.3.3.3)	(1) (3.3.3.3.3)	(3) (3.10.10)	(3) (3.10.10)
74	выпрямленный додекаэдр-икосаэдр	(1) (3.5.3.5)	(2) (3.4.5.4)	(1) (3.5.3.5)	(2) (3.4.5.4)
75	усеченный додекаэдр-икосаэдр	(1) (5.6.6)	(1) (3.4.5.4)	(1) (3.10.10)	(2) (4.6.10)
76	всенаправленный додекаэдр-икосаэдр	(1) (4.6.10)	(1) (4.6.10)	(1) (4.6.10)	(1) (4.6.10)
Неоднородный	всенаправленный додекаэдр-икосаэдр	(1) (3.3.3.3.5)	(1) (3.3.3.3.5)	(1) (3.3.3.3.5)	(1) (3.3.3.3.5)	(4) +(3.3.3)

Сводный перечень компактных однородных сот

Это полный перечень 76 однородных сот Wythoffian. В чередования перечислены для полноты, но большинство из них неоднородны.

Индекс	Группа Коксетера	Расширенный симметрия	Соты		Хиральный расширенный симметрия	Чередование сот
ЧАС1	${displaystyle {ar {BH}}_{3}}$ [4,3,5]	[4,3,5]	15	| | | | | | | | | | | |	[1^+,4,(3,5)^+]	(2)	(= )
					[4,3,5]^+	(1)
ЧАС2	${displaystyle {ar {J}}_{3}}$ [3,5,3]	[3,5,3]	6	| | | | |
		[2^+[3,5,3]]	5	| |	[2^+[3,5,3]]^+	(1)
ЧАС3	${displaystyle {ar {DH}}_{3}}$ [5,3^1,1]	[5,3^1,1]	4	| | |
		[1[5,3^1,1]]=[5,3,4] ↔	(7)	| | | | | |	[1[5,3^1,1]]^+ =[5,3,4]^+	(1)
ЧАС4	${displaystyle {widehat {AB}}_{3}}$ [(4,3,3,3)]	[(4,3,3,3)]	6	| | | | |
		[2^+[(4,3,3,3)]]	3	| |	[2^+[(4,3,3,3)]]^+	(1)
ЧАС5	${displaystyle {ar {K}}_{3}}$ [5,3,5]	[5,3,5]	6	| | | | |
		[2^+[5,3,5]]	3	| |	[2^+[5,3,5]]^+	(1)
ЧАС6	${displaystyle {widehat {AH}}_{3}}$ [(5,3,3,3)]	[(5,3,3,3)]	6	| | | | |
		[2^+[(5,3,3,3)]]	3	| |	[2^+[(5,3,3,3)]]^+	(1)
ЧАС7	${displaystyle {widehat {BB}}_{3}}$ [(3,4)^[2]]	[(3,4)^[2]]	2	|
		[2^+[(3,4)^[2]]]	1
		[2^+[(3,4)^[2]]]	1
		[2^+[(3,4)^[2]]]	1		[2^+[(3^+,4)^[2]]]	(1)
		[(2,2)^+[(3,4)^[2]]]	1		[(2,2)^+[(3,4)^[2]]]^+	(1)
ЧАС8	${displaystyle {widehat {BH}}_{3}}$ [(5,3,4,3)]	[(5,3,4,3)]	6	| | | | |
		[2^+[(5,3,4,3)]]	3	| |	[2^+[(5,3,4,3)]]^+	(1)
ЧАС9	${displaystyle {widehat {HH}}_{3}}$ [(3,5)^[2]]	[(3,5)^[2]]	2	|
		[2^+[(3,5)^[2]]]	1
		[2^+[(3,5)^[2]]]	1
		[2^+[(3,5)^[2]]]	1
		[(2,2)^+[(3,5)^[2]]]	1		[(2,2)^+[(3,5)^[2]]]^+	(1)

Смотрите также

• Равномерные мозаики в гиперболической плоскости
• Список правильных многогранников # Тесселяции гиперболического трехмерного пространства

Примечания

1. Хамфрис, 1990, стр. 141, 6.9 Список гиперболических групп Кокстера, рисунок 2 [1]
2. Феликсон, 2002 г.
3. Феликсон, 2002 г.
4. Венди Ю. Кригер, Стены и мосты: вид из шести измерений, Симметрия: культура и наука Том 16, номер 2, страницы 171–192 (2005) [2]
5. "Pd {3,5,3}".

Рекомендации

• Джеймс Э. Хамфрис, Группы отражений и группы Кокстера, Кембриджские исследования по высшей математике, 29 (1990)
• Красота геометрии: двенадцать эссе (1999), Dover Publications, LCCN  99-35678, ISBN  0-486-40919-8 (Глава 10, Регулярные соты в гиперболическом пространстве )
• Coxeter, Правильные многогранники, 3-й. изд., Dover Publications, 1973. ISBN  0-486-61480-8. (Таблицы I и II: Правильные многогранники и соты, стр. 294–296)
• Джеффри Р. Уикс Форма космоса, 2-е издание ISBN  0-8247-0709-5 (Главы 16-17: Геометрии на трехмерных многообразиях I, II) [3]
• Кокстеровские разложения гиперболических тетраэдров., arXiv /PDF, А. Феликсон, декабрь 2002 г.
• К. В. Л. Гарнер, Правильные косые многогранники в трехмерном гиперболическом пространстве Может. J. Math. 19, 1179–1186, 1967. PDF [4]
• Норман Джонсон, Геометрии и преобразования (2018), Главы 11,12,13
• Н. В. Джонсон, Р. Келлерхальс, Дж. Г. Рэтклифф, С. Т. Чанц, Размер гиперболического симплекса Кокстера, Transformation Groups 1999, Volume 4, Issue 4, pp 329–353. [5]
• N.W. Джонсон, Р. Келлерхальс, J.G. Рэтклифф, С. Чанц, Классы соизмеримости гиперболических групп Кокстера ЧАС³: p130. [6]
• Клитцинг, Ричард. «Гиперболические соты Н3 компакт».