Правильный косой многогранник - Regular skew polyhedron
В геометрия, то правильные косые многогранники являются обобщениями на множество правильные многогранники которые включают возможность неплоских лица или же фигуры вершин. Кокстер рассмотрел фигуры со скошенными вершинами, которые создали новые четырехмерные правильные многогранники, и намного позже Бранко Грюнбаум посмотрел на обычные косые лица.[1]
Бесконечные правильные косые многогранники, покрывающие 3-мерное пространство или выше, называются правильные косые апейроэдры.
История
В соответствии с Coxeter, в 1926 г. Джон Флиндерс Петри обобщил понятие правильные косые многоугольники (неплоские многоугольники) на правильные косые многогранники.
Кокстер предложил модифицированный Символ Шлефли {l, m | n} для этих фигур, причем {l, m} подразумевает вершина фигуры, м l-угольники вокруг вершины и п-гональные отверстия. Их вершинные фигуры перекос многоугольников, зигзагообразный между двумя плоскостями.
Правильные косые многогранники, представленные как {l, m | n}, подчиняются этому уравнению:
- 2 * cos (π / l) * cos (π / m) = cos (π / n)
Первый набор {l, m | n}, повторяет пять выпуклых Платоновы тела, и одна невыпуклая Твердое тело Кеплера-Пуансо:
| {l, m | n} | Лица | Края | Вершины | п | Многогранник | Симметрия порядок |
|---|---|---|---|---|---|---|
| {3,3| 3} = {3,3} | 4 | 6 | 4 | 0 | Тетраэдр | 12 |
| {3,4| 4} = {3,4} | 8 | 12 | 6 | 0 | Октаэдр | 24 |
| {4,3| 4} = {4,3} | 6 | 12 | 8 | 0 | Куб | 24 |
| {3,5| 5} = {3,5} | 20 | 30 | 12 | 0 | Икосаэдр | 60 |
| {5,3| 5} = {5,3} | 12 | 30 | 20 | 0 | Додекаэдр | 60 |
| {5,5| 3} = {5,5/2} | 12 | 30 | 12 | 4 | Большой додекаэдр | 60 |
Конечные правильные косые многогранники четырехмерного пространства
| A4 Самолет Кокстера прогнозы | |
|---|---|
 |  |
| {4, 6 | 3} | {6, 4 | 3} |
| Ранцинированный 5-клеточный (20 вершин, 60 ребер) | Bitruncated 5-элементный (30 вершин, 60 ребер) |
| Проекции плоскости Кокстера F4 | |
 |  |
| {4, 8 | 3} | {8, 4 | 3} |
| Ранцинированный 24-элементный (144 вершины, 576 ребер) | Урезанный 24-элементный (288 вершин, 576 ребер) |
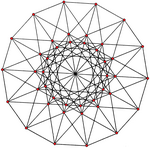 |  |
| {3,8|,4} = {3,8}8 | {4,6|,3} = {4,6}6 |
| 42 вершины, 168 ребер | 56 вершин, 168 ребер |
| Некоторые из 4-мерных правильных косых многогранников помещаются внутри однородной полихоры, как показано на верхних 4 проекциях. | |
Coxeter также перечислил большее количество конечных правильных многогранников в своей статье «Правильные косые многогранники в трех и четырех измерениях и их топологические аналоги».
Так же, как бесконечные косые многогранники представляют собой поверхности многообразия между ячейками выпуклые однородные соты, все конечные формы представляют собой поверхности многообразий внутри ячеек однородная полихора.
Многогранники вида {2p, 2q | r} связаны с Группа Кокстера симметрия [(p, r, q, r)], которая сводится к линейной [r, p, r], когда q равно 2. Кокстер дает эту симметрию как [[(п,р,q,р)]+] который, по его словам, изоморфен его абстрактная группа (2п,2q|2,р). Соответствующие соты имеют расширенную симметрию [[(п,р,q,р)]].[2]
{2p, 4 | r} представлен {2p} гранями усеченный битами {г, р, г} равномерный 4-многогранник, а {4,2p | r} представлен квадратными гранями разбитый {г, р, г}.
{4,4 | n} производит п-п дуопризма и, в частности, {4,4 | 4} помещается внутри {4} x {4} тессеракт.




| {l, m | n} | Лица | Края | Вершины | п | Структура | Симметрия | Заказ | Связанный однородная полихора |
|---|---|---|---|---|---|---|---|---|
| {4,4| 3} | 9 | 18 | 9 | 1 | D3xD3 | [[3,2,3]+] | 9 | 3-3 дуопризма |
| {4,4| 4} | 16 | 32 | 16 | 1 | D4xD4 | [[4,2,4]+] | 16 | 4-4 дуопризмы или тессеракт |
| {4,4| 5} | 25 | 50 | 25 | 1 | D5xD5 | [[5,2,5]+] | 25 | 5-5 дуопризма |
| {4,4| 6} | 36 | 72 | 36 | 1 | D6xD6 | [[6,2,6]+] | 36 | 6-6 дуопризма |
| {4,4 | n} | п2 | 2n2 | п2 | 1 | DпxDп | [[n, 2, n]+] | п2 | н-н дуопризма |
| {4,6| 3} | 30 | 60 | 20 | 6 | S5 | [[3,3,3]+] | 60 | Ранцинированный 5-клеточный |
| {6,4| 3} | 20 | 60 | 30 | 6 | S5 | [[3,3,3]+] | 60 | Bitruncated 5-элементный |
| {4,8| 3} | 288 | 576 | 144 | 73 | [[3,4,3]+] | 576 | Ранцинированный 24-элементный | |
| {8,4| 3} | 144 | 576 | 288 | 73 | [[3,4,3]+] | 576 | Урезанный 24-элементный |
| {l, m | n} | Лица | Края | Вершины | п | Структура | Симметрия | Заказ | Связанный однородная полихора |
|---|---|---|---|---|---|---|---|---|
| {4,5| 5} | 90 | 180 | 72 | 10 | A6 | [[5/2,5,5/2]+] | 360 | Runcinated большой звездчатый 120-элементный |
| {5,4| 5} | 72 | 180 | 90 | 10 | A6 | [[5/2,5,5/2]+] | 360 | Bitruncated большой звездчатый 120-элементный |
| {l, m | n} | Лица | Края | Вершины | п | Структура | Заказ |
|---|---|---|---|---|---|---|
| {4,5| 4} | 40 | 80 | 32 | 5 | ? | 160 |
| {5,4| 4} | 32 | 80 | 40 | 5 | ? | 160 |
| {4,7| 3} | 42 | 84 | 24 | 10 | НЧ (2,7) | 168 |
| {7,4| 3} | 24 | 84 | 42 | 10 | НЧ (2,7) | 168 |
| {5,5| 4} | 72 | 180 | 72 | 19 | A6 | 360 |
| {6,7| 3} | 182 | 546 | 156 | 105 | НЧ (2,13) | 1092 |
| {7,6| 3} | 156 | 546 | 182 | 105 | НЧ (2,13) | 1092 |
| {7,7| 3} | 156 | 546 | 156 | 118 | НЧ (2,13) | 1092 |
| {4,9| 3} | 612 | 1224 | 272 | 171 | НЧ (2,17) | 2448 |
| {9,4| 3} | 272 | 1224 | 612 | 171 | НЧ (2,17) | 2448 |
| {7,8| 3} | 1536 | 5376 | 1344 | 1249 | ? | 10752 |
| {8,7| 3} | 1344 | 5376 | 1536 | 1249 | ? | 10752 |
Окончательный набор основан на методе Кокстера. дальнейшая расширенная форма {q1, m | q2, q3 ...} или с неуказанным q2: {l, m |, q}. Их также можно представить в виде обычных конечная карта или же {л, м}2q, а группа Gл,м,q.[3]
| {л, м |, q} или же {л, м}2q | Лица | Края | Вершины | п | Структура | Заказ | Примечания |
|---|---|---|---|---|---|---|---|
| {3,6|,q} = {3,6}2q | 2q2 | 3q2 | q2 | 1 | грамм3,6,2q | 2q2 | |
| {3,2q|,3} = {3,2q}6 | 2кв.2 | 3кв.2 | 3кв. | (q-1)*(q-2)/2 | грамм3,6,2q | 2q2 | |
| {3,7|,4} = {3,7}8 | 56 | 84 | 24 | 3 | НЧ (2,7) | 168 | |
| {3,8|,4} = {3,8}8 | 112 | 168 | 42 | 8 | PGL (2,7) | 336 | Относится к сложный многогранник (1 1 114)4, |
| {4,6|,3} = {4,6}6 | 84 | 168 | 56 | 15 | PGL (2,7) | 336 | Относится к сложному многограннику (14 14 11)(3), |
| {3,7|,6} = {3,7}12 | 364 | 546 | 156 | 14 | НЧ (2,13) | 1092 | |
| {3,7|,7} = {3,7}14 | 364 | 546 | 156 | 14 | НЧ (2,13) | 1092 | |
| {3,8|,5} = {3,8}10 | 720 | 1080 | 270 | 46 | грамм3,8,10 | 2160 | Относится к сложному многограннику (1 1 114)5, |
| {3,10|,4} = {3,10}8 | 720 | 1080 | 216 | 73 | грамм3,8,10 | 2160 | Относится к сложному многограннику (1 1 115)4, |
| {4,6|,2} = {4,6}4 | 12 | 24 | 8 | 3 | S4 × S2 | 48 | |
| {5,6|,2} = {5,6}4 | 24 | 60 | 20 | 9 | A5 × S2 | 120 | |
| {3,11|,4} = {3,11}8 | 2024 | 3036 | 552 | 231 | НЧ (2,23) | 6072 | |
| {3,7|,8} = {3,7}16 | 3584 | 5376 | 1536 | 129 | грамм3,7,17 | 10752 | |
| {3,9|,5} = {3,9}10 | 12180 | 18270 | 4060 | 1016 | LF (2,29) × A3 | 36540 |
Высшие измерения
Правильные косые многогранники также могут быть построены в размерности больше 4 как вложения в правильные многогранники или соты. Например, правильный икосаэдр можно вложить в вершины 6-полукуб; это было названо правильный косой икосаэдр к Х. С. М. Коксетер. Аналогичным образом додекаэдр можно вложить в 10-полукуб.[4]
Смотрите также
Примечания
- ^ Абстрактные правильные многогранники, стр.7, стр.17
- ^ Кокстер, Правильные и полурегулярные многогранники II 2.34)
- ^ Кокстер и Мозер, Генераторы и отношения для дискретных групп, Раздел 8.6. Карты, имеющие заданные многоугольники Петри. п. 110
- ^ Деза, Майкл; Штогрин, Михаил (1998). «Вложение графов регулярных мозаик и звездных сот в графы гиперкубов и кубических решеток». Углубленное изучение чистой математики. Аранжировки - Токио 1998: 77. Дои:10.2969 / aspm / 02710073. ISBN 978-4-931469-77-8. Получено 4 апреля 2020.
Рекомендации
- Питер МакМаллен, Четырехмерные правильные многогранники, Дискретная и вычислительная геометрия, сентябрь 2007 г., том 38, выпуск 2, стр. 355–387
- Coxeter, Правильные многогранники, Третье издание, (1973), Дуврское издание, ISBN 0-486-61480-8
- Калейдоскопы: избранные произведения Х. С. М. Коксетер, под редакцией Ф. Артура Шерка, Питера Макмаллена, Энтони С. Томпсона, Асии Ивика Вайса, публикации Wiley-Interscience, 1995, ISBN 978-0-471-01003-6 [1]
- (Документ 2) H.S.M. Кокстер, "Правильные губки или косые многогранники", Scripta Mathematica 6 (1939) 240-244.
- (Документ 22) Х.С.М. Кокстер, Регулярные и полурегулярные многогранники I, [Math. Zeit. 46 (1940) 380–407, MR 2,10]
- (Документ 23) Х.С.М. Кокстер, Правильные и полурегулярные многогранники II, [Math. Zeit. 188 (1985) 559–591]
- Coxeter, Красота геометрии: двенадцать эссе, Dover Publications, 1999 г., ISBN 0-486-40919-8 (Глава 5: Правильные косые многогранники в трех и четырех измерениях и их топологические аналоги, Труды Лондонского математического общества, сер. 2, том 43, 1937.)
- Кокстер, Х. С. М. Правильные косые многогранники в трех и четырех измерениях. Proc. Лондонская математика. Soc. 43, 33-62, 1937.
- Гарнер, К. В. Л. Правильные косые многогранники в трехмерном гиперболическом пространстве. Может. J. Math. 19, 1179-1186, 1967.
- Э. Шульте, Дж. М. Уиллс О правильных косых многогранниках Кокстера // Дискретная математика, том 60, июнь – июль 1986 г., страницы 253–262.
