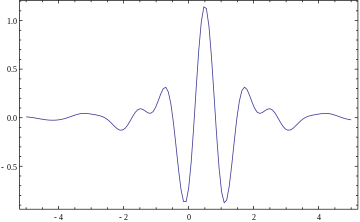
Вейвлет - Wavelet
А вейвлет это волна -подобно колебание с амплитуда который начинается с нуля, увеличивается, а затем снова уменьшается до нуля. Обычно это можно представить как «кратковременное колебание», подобное зарегистрированному сейсмограф или же монитор сердца. Как правило, вейвлеты специально создаются для того, чтобы иметь определенные свойства, которые делают их полезными для обработка сигналов. С помощью свертка, вейвлеты могут быть объединены с известными частями поврежденного сигнала для извлечения информации из неизвестных частей.
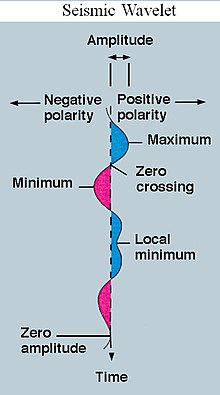
Например, можно создать вейвлет с частотой Средний C и короткая продолжительность примерно 32-я нота. Если бы этот вейвлет был свернут с сигналом, созданным из записи мелодии, то полученный сигнал был бы полезен для определения того, когда в песне игралась средняя нота C. Математически вейвлет будет коррелировать с сигналом, если неизвестный сигнал содержит информацию аналогичной частоты. Эта концепция корреляция лежит в основе многих практических приложений теории всплесков.
В качестве математического инструмента вейвлеты могут использоваться для извлечения информации из множества различных типов данных, включая, помимо прочего, звуковые сигналы и изображения. Наборы вейвлетов обычно необходимы для полного анализа данных. Набор «дополнительных» вейвлетов будет разлагать данные без пропусков или перекрытий, так что процесс разложения будет математически обратимым. Таким образом, наборы дополнительных вейвлетов полезны в сжатие на основе вейвлетов / декомпрессии, где желательно восстановить исходную информацию с минимальными потерями.
Формально это представление является серия вейвлетов представление квадратично интегрируемая функция в отношении либо полный, ортонормированный набор из базисные функции, или переполнен установить или рамка векторного пространства, для Гильбертово пространство квадратично интегрируемых функций. Это достигается через когерентные состояния.
Имя
Слово вейвлет десятилетиями использовался в цифровой обработке сигналов и разведочной геофизике.[1] Эквивалент Французский слово Онделетт значение "малая волна" использовалось Морле и Гроссманн в начале 1980-х гг.
Теория вейвлетов
Теория вейвлетов применима к нескольким предметам. Все вейвлет-преобразования можно рассматривать как формы частотно-временное представление за непрерывное время (аналоговые) сигналы и поэтому относятся к гармонический анализ. Дискретное вейвлет-преобразование (непрерывное во времени) дискретное время (дискретизированный) сигнал с помощью дискретное время банки фильтров диадической (октавной полосы) конфигурации является вейвлет-приближением этого сигнала. Коэффициенты такого банка фильтров называются коэффициентами вейвлета и масштабирования в номенклатуре вейвлетов. Эти наборы фильтров могут содержать либо конечная импульсная характеристика (FIR) или бесконечный импульсный отклик (БИХ) фильтры. Вейвлеты, образующие непрерывное вейвлет-преобразование (CWT) подлежат принцип неопределенности соответствующей теории выборки: учитывая сигнал с некоторым событием в нем, нельзя одновременно присвоить этому событию точное время и шкалу частотной характеристики. Произведение неопределенностей шкалы времени и частотной характеристики имеет нижнюю границу. Таким образом, в скейлограмма непрерывного вейвлет-преобразования этого сигнала, такое событие отмечает всю область на шкале времени, а не только одну точку. Кроме того, дискретные вейвлет-основы можно рассматривать в контексте других форм принципа неопределенности.[2][3][4][5]
Вейвлет-преобразования в целом делятся на три класса: непрерывные, дискретные и основанные на множественном разрешении.
Непрерывные вейвлет-преобразования (параметры непрерывного сдвига и масштабирования)
В непрерывные вейвлет-преобразования, данный сигнал конечной энергии проецируется на непрерывное семейство частотных диапазонов (или аналогичные подпространства Lп функциональное пространство L2(р)). Например, сигнал может быть представлен на каждой полосе частот в форме [ж, 2ж] для всех положительных частот ж > 0. Затем исходный сигнал можно восстановить путем подходящего интегрирования по всем результирующим частотным компонентам.
Полосы частот или подпространства (подполосы) являются масштабированными версиями подпространства в масштабе 1. Это подпространство, в свою очередь, в большинстве ситуаций генерируется сдвигами одной производящей функции ψ в L2(р), материнский вейвлет. Для примера масштабирования одной полосы частот [1, 2] эта функция
с (нормализованным) функция sinc. Это, Мейер и два других примера материнских вейвлетов:
Подпространство масштаба а или частотный диапазон [1 /а, 2/а] генерируется функциями (иногда называемыми дочерние вейвлеты)
куда а положительна и определяет масштаб и б - любое действительное число и определяет сдвиг. Пара (а, б) определяет точку в правой полуплоскости р+ × р.
Проекция функции Икс на подпространство масштаба а тогда имеет вид
с вейвлет-коэффициенты
Для анализа сигнала Икс, можно собрать вейвлет-коэффициенты в скейлограмма сигнала.
См. Список некоторых Непрерывные вейвлеты.
Дискретные вейвлет-преобразования (дискретные параметры сдвига и масштаба, непрерывные во времени)
С вычислительной точки зрения невозможно проанализировать сигнал с использованием всех вейвлет-коэффициентов, поэтому можно задаться вопросом, достаточно ли выбрать дискретное подмножество верхней полуплоскости, чтобы иметь возможность восстановить сигнал из соответствующих вейвлет-коэффициентов. Одна из таких систем - аффинный система для некоторых реальных параметров а > 1, б > 0. Соответствующее дискретное подмножество полуплоскости состоит из всех точек (ам, намб) с м, п в Z. Соответствующие дочерние вейвлеты теперь даны как
Достаточное условие для восстановления любого сигнала Икс конечной энергии по формуле
в том, что функции для мужчин ортонормированный базис из L2(р).
Дискретные вейвлет-преобразования на основе множественного разрешения (непрерывные во времени)

В любом дискретизированном вейвлет-преобразовании существует только конечное число вейвлет-коэффициентов для каждой ограниченной прямоугольной области в верхней полуплоскости. Тем не менее, каждый коэффициент требует вычисления интеграла. В особых ситуациях этой числовой сложности можно избежать, если масштабированные и сдвинутые вейвлеты образуют анализ с несколькими разрешениями. Это означает, что должна существовать вспомогательная функция, отец вейвлет φ в L2(р), и что а целое число. Типичный выбор: а = 2 и б = 1. Самая известная пара вейвлетов отца и матери - это Добеши Вейвлет с 4 нажатиями. Обратите внимание, что не каждый ортонормированный дискретный вейвлет-базис может быть связан с анализом с множественным разрешением; например, вейвлет Журна не допускает анализа с множественным разрешением.[6]
Из вейвлетов матери и отца строятся подпространства
Отцовский вейвлет сохраняет свойства временной области, в то время как материнские вейвлеты сохраняет свойства частотной области.
Из них требуется, чтобы последовательность
образует анализ с несколькими разрешениями из L2 и что подпространства являются ортогональными «разностями» указанной выше последовательности, то есть Wм ортогональное дополнение к Vм внутри подпространства Vм−1,
По аналогии с теорема выборки можно сделать вывод, что пространство Vм с расстоянием выборки 2м более-менее охватывает полосу частот от 0 до 2−м-1. В качестве ортогонального дополнения Wм примерно покрывает полосу [2−м−1, 2−м].
Из этих включений и соотношений ортогональности, особенно , следует за существованием последовательностей и которые удовлетворяют тождества
- так что и
- так что
Вторая идентичность первой пары - это уточняющее уравнение для отцовского вейвлета φ. Обе пары тождеств составляют основу алгоритма быстрое вейвлет-преобразование.
Из анализа кратного разрешения выводится ортогональное разложение пространства L2 в качестве
Для любого сигнала или функции это дает представление в базисных функциях соответствующих подпространств как
где коэффициенты
- и
- .
Материнский вейвлет
Для практических приложений и из соображений эффективности предпочтение отдается непрерывно дифференцируемым функциям с компактной опорой в качестве материнского (прототипа) вейвлета (функций). Однако, чтобы удовлетворить аналитические требования (в непрерывном WT) и в целом по теоретическим причинам, каждый выбирает вейвлет-функции из подпространства Космос Это пространство измеримые функции которые (по абсолютной величине) квадратные интегрируемый:
- и
Пребывание в этом пространстве гарантирует, что можно сформулировать условия нулевого среднего и квадратичной нормы один:
- - условие нулевого среднего, а
- является условием квадратичной нормы один.
Чтобы ψ было вейвлетом для непрерывное вейвлет-преобразование (см. там точное утверждение), материнский вейвлет должен удовлетворять критерию допустимости (грубо говоря, разновидности полудифференцируемости), чтобы получить стабильно обратимое преобразование.
Для дискретное вейвлет-преобразование, нужно хотя бы условие, что серия вейвлетов является представлением тождества в Космос L2(р). Большинство конструкций дискретных БТ используют анализ с несколькими разрешениями, который определяет вейвлет с помощью функции масштабирования. Эта функция масштабирования сама по себе является решением функционального уравнения.
В большинстве случаев полезно ограничить ψ непрерывной функцией с большим числом M исчезающих моментов, т.е.для всех целых м < M
Материнский вейвлет масштабируется (или расширяется) с коэффициентом а и переведены (или сдвинуты) с коэффициентом б дать (согласно первоначальной формулировке Морле):
Для непрерывного ВП пара (а,б) меняется на всей полуплоскости р+ × р; для дискретного WT эта пара изменяется на его дискретном подмножестве, которое также называется аффинная группа.
Эти функции часто неправильно называют базисными функциями (непрерывного) преобразования. Фактически, как и в случае непрерывного преобразования Фурье, в непрерывном вейвлет-преобразовании нет основы. Частотно-временная интерпретация использует несколько иную формулировку (по Дельпрату).
Ограничение :
(1) когда a1 = a и b1 = b,
(2) имеет конечный интервал времени
Сравнение с преобразованием Фурье (непрерывное время)
Вейвлет-преобразование часто сравнивают с преобразование Фурье, в котором сигналы представлены в виде суммы синусоид. Фактически, преобразование Фурье можно рассматривать как частный случай непрерывного вейвлет-преобразования с выбором материнского вейвлетаОсновное отличие в целом состоит в том, что вейвлеты локализованы как по времени, так и по частоте, тогда как стандартные преобразование Фурье локализован только в частота. В Кратковременное преобразование Фурье (STFT) аналогичен вейвлет-преобразованию в том, что он также локализован по времени и частоте, но есть проблемы с компромиссом между частотным / временным разрешением.
В частности, предполагая прямоугольную область окна, можно думать о STFT как о преобразовании с немного другим ядром
куда часто можно записать как , куда и u соответственно обозначают длину и временное смещение оконной функции. С помощью Теорема Парсеваля, можно определить энергию вейвлета как
Отсюда квадрат временной поддержки окна, смещенного по времени u, определяется как
и квадрат спектральной опоры окна, действующего на частоту
Умножение с прямоугольным окном во временной области соответствует свертке с функция в частотной области, что приводит к ложным звенящие артефакты для коротких / локализованных временных окон. С помощью преобразования Фурье с непрерывным временем и эта свертка выполняется с дельта-функцией в пространстве Фурье, что приводит к истинному преобразованию Фурье сигнала . Оконная функция может быть другой аподизирующий фильтр, например Гауссовский. Выбор оконной функции повлияет на ошибку аппроксимации относительно истинного преобразования Фурье.
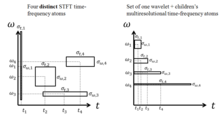
С помощью STFT нельзя превышать произведение времени и ширины ячейки с заданным разрешением. Все базовые элементы STFT поддерживают равномерную спектральную и временную поддержку для всех временных сдвигов или смещений, тем самым достигая одинакового разрешения во времени для низких и высоких частот. Разрешение определяется исключительно шириной выборки.
Напротив, вейвлет-преобразование многоуровневый properties обеспечивает большую временную поддержку для более низких частот при сохранении короткой временной ширины для более высоких частот за счет свойств масштабирования вейвлет-преобразования. Это свойство расширяет обычный частотно-временной анализ на анализ в масштабе времени.[7]
Дискретное вейвлет-преобразование требует меньше вычислений. сложный, принимая O (N) время по сравнению с O (N бревноN) для быстрое преобразование Фурье. Это вычислительное преимущество не присуще преобразованию, но отражает выбор логарифмического деления частоты, в отличие от равномерного частотного деления БПФ (быстрое преобразование Фурье), которое использует те же базисные функции, что и ДПФ (дискретное преобразование Фурье). .[8] Также важно отметить, что эта сложность применима только тогда, когда размер фильтра не имеет отношения к размеру сигнала. Вейвлет без компактная опора такой как Вейвлет Шеннона потребует O (N2). (Например, существует также логарифмическое преобразование Фурье с O (N) сложности, но исходный сигнал должен быть дискретизирован логарифмически по времени, что полезно только для определенных типов сигналов.[9])
Определение вейвлета
Существует несколько способов определения вейвлета (или семейства вейвлетов).
Масштабирующий фильтр
Ортогональный вейвлет полностью определяется масштабным фильтром - низкочастотным фильтром. конечная импульсная характеристика (FIR) фильтр длины 2N и сумма 1. В биортогональный определены вейвлеты, отдельные фильтры разложения и восстановления.
Для анализа с ортогональными вейвлетами фильтр высоких частот рассчитывается как квадратурный зеркальный фильтр фильтра нижних частот и фильтры восстановления являются обратными по времени фильтрами разложения.
Вейвлеты Добеши и Симлета могут быть определены с помощью масштабирующего фильтра.
Функция масштабирования
Вейвлеты определяются вейвлет-функцией ψ (т) (т. е. материнский вейвлет) и функцию масштабирования φ (т) (также называемый отцовским вейвлетом) во временной области.
Вейвлет-функция по сути является полосовым фильтром, масштабирование которого для каждого уровня уменьшает вдвое его полосу пропускания. Это создает проблему, заключающуюся в том, что для покрытия всего спектра потребуется бесконечное количество уровней. Функция масштабирования фильтрует самый низкий уровень преобразования и обеспечивает охват всего спектра. Видеть[10] для подробного объяснения.
Для вейвлета с компактной опорой φ (т) можно считать конечной по длине и эквивалентен масштабному фильтру грамм.
Вейвлеты Мейера могут быть определены с помощью функций масштабирования
Вейвлет-функция
Вейвлет имеет представление только во временной области как вейвлет-функция ψ (т).
Например, Мексиканские вейвлеты в шляпе можно определить с помощью вейвлет-функции. См. Список из нескольких Непрерывные вейвлеты.
История
Развитие вейвлеты можно связать с несколькими отдельными направлениями мысли, начиная с Хаар работы в начале 20 века. Позже работа Деннис Габор уступил Атомы Габора (1946), которые построены аналогично вейвлетам и применяются для аналогичных целей.
Вейвлет-сжатие, форма преобразование кодирования который использует вейвлет-преобразования в Сжатие данных, началось после разработки дискретное косинусное преобразование (DCT),[11] блочный Сжатие данных алгоритм, впервые предложенный Насир Ахмед в начале 1970-х гг.[12][13] Внедрение DCT привело к развитию вейвлет-кодирования, варианта DCT-кодирования, в котором вместо блочного алгоритма DCT используются вейвлеты.[11]
С тех пор значительный вклад в теорию вейвлетов можно отнести к Цвейг Открытие непрерывное вейвлет-преобразование (CWT) в 1975 году (первоначально называвшееся преобразованием улитки и обнаруженное при изучении реакции уха на звук),[14] Пьер Гупийо, Гроссманн и Морле формулировка того, что сейчас известно как CWT (1982), ранняя работа Ян-Олова Стрёмберга по дискретные вейвлеты (1983), вейвлет LeGall-Tabatabai (LGT) 5/3, разработанный Дидье Ле Галлом и Али Дж. Табатабаи (1988),[15][16][17] Ингрид Добешис 'ортогональные всплески с компактной опорой (1988 г.), Маллат концепция множественного разрешения (1989), Али Акансу с Биномиальный QMF (1990), частотно-временная интерпретация CWT Натали Дельпрат (1991), Newland's гармоническое вейвлет-преобразование (1993), и установить разделение в иерархических деревьях (SPIHT), разработанный Амиром Саидом совместно с Уильямом А. Перлманом в 1996 году.[18]
В JPEG 2000 стандарт был разработан с 1997 по 2000 год Объединенная группа экспертов в области фотографии (JPEG) комитет под председательством Тураджа Эбрахими (позже президент JPEG).[19] В отличие от алгоритма DCT, использованного в исходном JPEG формат, JPEG 2000 вместо этого использует дискретное вейвлет-преобразование (DWT) алгоритмы. Он использует CDF Вейвлет-преобразование 9/7 (разработанное Ингрид Добешис в 1992 г.) для сжатие с потерями алгоритм и вейвлет-преобразование ЛеГалла-Табатабаи (LGT) 5/3 (разработанное Дидье Ле Галлом и Али Дж. Табатабаи в 1988 г.) для его сжатие без потерь алгоритм.[20] JPEG 2000 технология, которая включает Motion JPEG 2000 расширение, было выбрано в качестве стандарт кодирования видео за цифровое кино в 2004 г.[21]
График
- Первый вейвлет (Вейвлет Хаара ) к Альфред Хаар (1909)
- С 1970-х гг .: Джордж Цвейг, Жан Морле, Алекс Гроссманн
- С 1980-х: Ив Мейер, Дидье Ле Галл, Али Дж. Табатабай, Стефан Малла, Ингрид Добешис, Рональд Койфман, Али Акансу, Виктор Викерхаузер
- С 1990-х: Натали Дельпрат, Ньюленд, Амир Саид, Уильям А. Перлман, Турадж Эбрахими, JPEG 2000
Вейвлет-преобразования
Вейвлет - это математическая функция, используемая для деления заданной функции или непрерывный сигнал на компоненты разного масштаба. Обычно каждому компоненту шкалы можно присвоить частотный диапазон. Затем можно изучить каждый компонент шкалы с разрешением, соответствующим его масштабу. Вейвлет-преобразование - это представление функции вейвлетами. Вейвлеты масштабированный и переведено копии (известные как «дочерние вейвлеты») конечной длины или быстро затухающие осциллирующие волны (известные как «материнские вейвлеты»). Вейвлет-преобразования имеют преимущества перед традиционными Преобразования Фурье для представления функций, которые имеют разрывы и острые пики, и для точной деконструкции и восстановления конечных, непериодический и / или нестационарный сигналы.
Вейвлет-преобразования подразделяются на дискретные вейвлет-преобразования (DWT) и непрерывные вейвлет-преобразования (CWTs). Обратите внимание, что как DWT, так и CWT являются непрерывными (аналоговыми) преобразованиями. Их можно использовать для представления (аналоговых) сигналов с непрерывным временем. CWT работают со всеми возможными масштабами и перемещениями, тогда как DWT используют определенное подмножество значений масштаба и перемещения или сетку представления.
Существует большое количество вейвлет-преобразований, каждое из которых подходит для разных приложений. Полный список см. список преобразований, связанных с вейвлетами но наиболее распространенные из них перечислены ниже:
- Непрерывное вейвлет-преобразование (CWT)
- Дискретное вейвлет-преобразование (DWT)
- Быстрое вейвлет-преобразование (FWT)
- Схема подъема & Обобщенная схема подъема
- Разложение вейвлет-пакета (WPD)
- Стационарное вейвлет-преобразование (SWT)
- Дробное преобразование Фурье (FRFT)
- Дробное вейвлет-преобразование (FRWT)
Обобщенные преобразования
Существует ряд обобщенных преобразований, частным случаем которых является вейвлет-преобразование. Например, Йосеф Джозеф Сегман ввел масштаб в Группа Гейзенберга, что приводит к непрерывному пространству преобразования, которое является функцией времени, масштаба и частоты. CWT - это двухмерный срез полученного трехмерного объема в масштабе времени и частоте.
Другой пример обобщенного преобразования - это преобразование chirplet в котором CWT также представляет собой двумерный срез через преобразование chirplet.
Важной областью применения обобщенных преобразований являются системы, в которых решающее значение имеет высокое разрешение по частоте. Например, темное поле электронно-оптические преобразования промежуточные между прямым и взаимное пространство широко использовались в гармонический анализ кластеризации атомов, т.е. при изучении кристаллы и кристаллические дефекты.[22] Теперь, когда просвечивающие электронные микроскопы способны предоставлять цифровые изображения с пикометровой информацией об атомной периодичности в наноструктура всех видов, диапазон распознавание образов[23] и напряжение[24]/метрология[25] приложения для промежуточных преобразований с высоким частотным разрешением (например, кисти[26] и риджлеты[27]) быстро растет.
Дробное вейвлет-преобразование (FRWT) - это обобщение классического вейвлет-преобразования в областях дробного преобразования Фурье. Это преобразование позволяет одновременно предоставлять информацию во временной и дробной областях и представлять сигналы в плоскости дробно-временной области.[28]
Приложения вейвлет-преобразования
Как правило, приближение к DWT используется для Сжатие данных если сигнал уже выбран, и CWT для анализ сигналов.[29] Таким образом, приближение DWT обычно используется в инженерии и информатике, а CWT - в научных исследованиях.
Как и некоторые другие преобразования, вейвлет-преобразования могут использоваться для преобразования данных, а затем для кодирования преобразованных данных, что приводит к эффективному сжатию. Например, JPEG 2000 стандарт сжатия изображений, использующий биортогональные вейвлеты. Это означает, что несмотря на то, что фрейм заполнен с избытком, это плотная рамка (см. типы рамки векторного пространства ), и одни и те же фрейм-функции (за исключением сопряжения в случае сложных вейвлетов) используются как для анализа, так и для синтеза, т.е. как в прямом, так и в обратном преобразовании. Подробнее см. вейвлет-сжатие.
Связанное использование предназначено для сглаживания / уменьшения шума данных на основе порогового значения вейвлет-коэффициента, также называемого сжатием вейвлет-сигнала. Посредством адаптивного определения порога вейвлет-коэффициентов, которые соответствуют нежелательным частотным компонентам, могут выполняться операции сглаживания и / или удаления шума.
Вейвлет-преобразования также начинают использоваться для коммуникационных приложений. Вейвлет OFDM это основная схема модуляции, используемая в HD-PLC (а линии электропередач технология, разработанная Panasonic ), и в одном из дополнительных режимов, включенных в IEEE 1901 стандарт. Вейвлет OFDM может обеспечить более глубокие выемки, чем традиционные БПФ OFDM и вейвлет OFDM не требуют защитного интервала (который обычно представляет собой значительные накладные расходы в системах FFT OFDM).[30]
Как представление сигнала
Часто сигналы могут быть представлены в виде суммы синусоид. Однако рассмотрите прерывистый сигнал с резким разрывом; этот сигнал все еще может быть представлен в виде суммы синусоид, но требует бесконечного числа, что является наблюдением, известным как Феномен Гиббса. Таким образом, для этого требуется бесконечное количество коэффициентов Фурье, что непрактично для многих приложений, таких как сжатие. Вейвлеты более полезны для описания этих сигналов с разрывами из-за их локализованного во времени поведения (и преобразования Фурье, и вейвлет-преобразования локализованы по частоте, но вейвлеты обладают дополнительным свойством локализации во времени). Из-за этого на практике многие типы сигналов могут быть не разреженными в области Фурье, но очень разреженными в области вейвлетов. Это особенно полезно при реконструкции сигналов, особенно в недавно популярной области сжатое зондирование. (Обратите внимание, что кратковременное преобразование Фурье (STFT) также локализован по времени и частоте, но часто возникают проблемы с соотношением частотно-временного разрешения. Вейвлеты лучше представляют сигнал из-за анализ с несколькими разрешениями.)
Это мотивирует то, почему вейвлет-преобразования теперь применяются для огромного количества приложений, часто заменяя обычные преобразование Фурье. Этот сдвиг парадигмы произошел во многих областях физики, включая молекулярная динамика, теория хаоса,[31] ab initio расчеты, астрофизика, гравитационная волна анализ переходных данных,[32][33] матрица плотности локализация, сейсмология, оптика, турбулентность и квантовая механика. Это изменение также произошло в обработка изображений, ЭЭГ, ЭМГ,[34] ЭКГ анализы, ритмы мозга, ДНК анализ, белок анализ, климатология, анализ сексуальной реакции человека,[35] Общее обработка сигналов, распознавание речи, акустика, вибросигналы,[36] компьютерная графика, мультифрактальный анализ, и разреженное кодирование. В компьютерное зрение и обработка изображений, понятие масштабное пространство операторы представления и производной Гаусса рассматриваются как каноническое многомасштабное представление.
Вейвлет-шумоподавление
Допустим, мы измеряем зашумленный сигнал . Предположим, что s имеет разреженное представление в определенных базисах вейвлетов, и
Так .
Большинство элементов в p равны 0 или близки к 0, и
Поскольку W ортогонален, задача оценки сводится к восстановлению сигнала в iid Гауссов шум. Поскольку p является разреженным, одним из методов является применение модели смеси Гаусса для p.
Предположим, что , - дисперсия "значимых" коэффициентов, а - дисперсия «незначительных» коэффициентов.
потом , называется коэффициентом усадки, который зависит от предварительных отклонений и . Эффект коэффициента усадки заключается в том, что малые коэффициенты заранее устанавливаются на 0, а большие коэффициенты не меняются.
Маленькие коэффициенты - это в основном шумы, а большие коэффициенты содержат фактический сигнал.
Наконец, примените обратное вейвлет-преобразование, чтобы получить
Список вейвлетов
Дискретные вейвлеты
- Бейлкин (18)
- Вейвлеты BNC
- Coiflet (6, 12, 18, 24, 30)
- Вейвлет Коэна-Добеши-Фово (Иногда их называют CDF N / P или биортогональные вейвлеты Добеши)
- Вейвлет Добеши (2, 4, 6, 8, 10, 12, 14, 16, 18, 20 и т. Д.)
- Биномиальный-QMF (Также называется вейвлетом Добеши)
- Вейвлет Хаара
- Вейвлет Матьё
- Вейвлет Лежандра
- Вейвлет Вилласенора
- Симлет[37]
Непрерывные вейвлеты
С реальной ценностью
- Бета-вейвлет
- Эрмитов вейвлет
- Вейвлет эрмитовой шляпы
- Вейвлет Мейера
- Мексиканская шляпа вейвлет
- Вейвлет Пуассона
- Вейвлет Шеннона
- Сплайн вейвлет
- Вейвлет Стрёмберга
Комплекснозначный
- Сложный мексиканский вейвлет шляпы
- fbsp вейвлет
- Вейвлет Морле
- Вейвлет Шеннона
- Модифицированный вейвлет Морле
Смотрите также
- Чирплет преобразование
- Curvelet
- Цифровое кино
- Банки фильтров
- Фрактальное сжатие
- Дробное преобразование Фурье
- JPEG 2000
- Анализ с несколькими разрешениями
- Noiselet
- Неразделимый вейвлет
- Масштабировать пространство
- Масштабированная корреляция
- Shearlet
- Кратковременное преобразование Фурье
- Сверхширокополосный радио - передает вейвлеты
- Волновой пакет
- Вейвлет Габора # Пространство вейвлетов[38]
- Уменьшение размеров
- Преобразования, связанные с Фурье
- Спектрограмма
- Принцип Гюйгенса – Френеля (физические вейвлеты)
Рекомендации
Цитаты
- ^ Рикер, Норман (1953). «Сокращение вейвлета, расширение вейвлета и контроль сейсмического разрешения». Геофизика. 18 (4): 769–792. Bibcode:1953Геоп ... 18..769R. Дои:10.1190/1.1437927.
- ^ Мейер, Ив (1992), Вейвлеты и операторы, Кембридж, Великобритания: Cambridge University Press, ISBN 0-521-42000-8
- ^ Чуи, Чарльз К. (1992), Введение в вейвлеты, Сан-Диего, Калифорния: Academic Press, ISBN 0-12-174584-8
- ^ Добеши, Ингрид. (1992), Десять лекций по вейвлетам, SIAM, ISBN 978-0-89871-274-2
- ^ Акансу, Али Н .; Хаддад, Ричард А. (1992), Разложение сигнала с несколькими разрешениями: преобразования, поддиапазоны и всплески, Бостон, Массачусетс: Academic Press, ISBN 978-0-12-047141-6
- ^ Ларсон, Дэвид Р. (2007). «Вейвлет-анализ и приложения (см .: Унитарные системы и наборы вейвлетов)». Appl. Нумер. Хармон. Анальный. Биркхойзер: 143–171. Цитировать журнал требует
| журнал =(помощь) - ^ Маллат, Стефан. "Вейвлет-тур по обработке сигналов. 1998." 250-252.
- ^ Руководство для ученых и инженеров по цифровой обработке сигналов Стивена В. Смита, доктора философии. Глава 8 уравнение 8-1: http://www.dspguide.com/ch8/4.htm
- ^ http://homepages.dias.ie/~ajones/publications/28.pdf
- ^ "Действительно удобный справочник по вейвлетам - PolyValens". www.polyvalens.com.
- ^ а б Хоффман, Рой (2012). Сжатие данных в цифровых системах. Springer Science & Business Media. п. 124. ISBN 9781461560319.
По сути, вейвлет-кодирование - это вариант кодирования с преобразованием на основе DCT, который уменьшает или устраняет некоторые из его ограничений. (...) Еще одно преимущество заключается в том, что вместо работы с блоками 8 × 8 пикселей, как это делают JPEG и другие блочные методы DCT, вейвлет-кодирование может одновременно сжимать все изображение.
- ^ Ахмед, Насир (Январь 1991 г.). «Как я пришел к дискретному косинусному преобразованию». Цифровая обработка сигналов. 1 (1): 4–5. Дои:10.1016 / 1051-2004 (91) 90086-Z.
- ^ Станкович, Радомир С .; Астола, Яакко Т. (2012). «Воспоминания о ранних работах в DCT: интервью с К.Р. Рао» (PDF). Отпечатки с первых дней информационных наук. 60. Получено 13 октября 2019.
- ^ http://scienceworld.wolfram.com/biography/Zweig.html Цвейг, Джордж Биография на Scienceworld.wolfram.com
- ^ Салливан, Гэри (8–12 декабря 2003 г.). «Общие характеристики и конструктивные соображения для кодирования видео временного поддиапазона». ITU-T. Группа экспертов по кодированию видео. Получено 13 сентября 2019.
- ^ Бовик, Алан С. (2009). Основное руководство по обработке видео. Академическая пресса. п. 355. ISBN 9780080922508.
- ^ Галл, Дидье Ле; Табатабай, Али Дж. (1988). «Подполосное кодирование цифровых изображений с использованием симметричных коротких ядерных фильтров и методов арифметического кодирования». ICASSP-88., Международная конференция по акустике, речи и обработке сигналов: 761–764 т.2. Дои:10.1109 / ICASSP.1988.196696. S2CID 109186495.
- ^ Сказал, Амир; Перлман, Уильям А. (июнь 1996 г.). «Новый быстрый и эффективный кодек изображений, основанный на разделении множеств в иерархических деревьях». IEEE Transactions по схемам и системам для видеотехнологий. 6 (3): 243–250. Дои:10.1109/76.499834. ISSN 1051-8215.
- ^ Таубман, Дэвид; Марселлин, Майкл (2012). JPEG2000: основы, стандарты и практика сжатия изображений: основы, стандарты и практика сжатия изображений. Springer Science & Business Media. ISBN 9781461507994.
- ^ Unser, M .; Блю Т. (2003). «Математические свойства вейвлет-фильтров JPEG2000» (PDF). IEEE Transactions по обработке изображений. 12 (9): 1080–1090. Дои:10.1109 / TIP.2003.812329. PMID 18237979. S2CID 2765169.
- ^ Шварц, Чарльз С. (2005). Понимание цифрового кино: профессиональное руководство. Тейлор и Фрэнсис. п. 147. ISBN 9780240806174.
- ^ П. Хирш, А. Хауи, Р. Николсон, Д. У. Пэшли и М. Дж. Уилан (1965/1977) Электронная микроскопия тонких кристаллов (Баттервортс, Лондон / Кригер, Малабар, Флорида) ISBN 0-88275-376-2
- ^ П. Фраундорф, Дж. Ван, Э. Манделл и М. Роуз (2006) Цифровые таблицы темного поля, Микроскопия и микроанализ 12: S2, 1010–1011 (ср. arXiv: cond-mat / 0403017 )
- ^ Htch, M. J .; Snoeck, E .; Килаас, Р. (1998). «Количественное измерение полей смещения и деформации по микрофотографиям ПЭМВР». Ультрамикроскопия. 74 (3): 131–146. Дои:10.1016 / s0304-3991 (98) 00035-7.
- ^ Мартин Роуз (2006) Измерение расстояния между полосами решетки на изображении HRTEM с использованием цифрового разложения темного поля (Магистерская диссертация по физике, США, Миссури, Сент-Луис)
- ^ Ф. Г. Мейер и Р. Р. Койфман (1997) Прикладной и вычислительный гармонический анализ 4:147.
- ^ А.Г. Флеся, Х. Хель-Ор, А. Авербух, Э. Дж. Кандес, Р. Р. Койфман и Д. Л. Донохо (2001) Цифровая реализация риджлет-пакетов (Академик Пресс, Нью-Йорк).
- ^ Shi, J .; Zhang, N.-T .; Лю, X.-P. (2011). «Новое дробное вейвлет-преобразование и его приложения». Sci. China Inf. Наука. 55 (6): 1270–1279. Дои:10.1007 / s11432-011-4320-х.
- ^ А.Н. Акансу, В.А.Сердейн и И.В. Селесник, Новые приложения вейвлетов: обзор, Физическая коммуникация, Elsevier, т. 3, выпуск 1, стр. 1-18, март 2010 г.
- ^ Стефано Галли; О. Логвинов (июль 2008 г.). «Последние разработки в области стандартизации линий электропередач в рамках IEEE». Журнал IEEE Communications. 46 (7): 64–71. Дои:10.1109 / MCOM.2008.4557044. S2CID 2650873. Обзор предложения P1901 PHY / MAC.
- ^ Wotherspoon, T .; и другие. (2009). «Адаптация к краю хаоса со случайной вейвлет-обратной связью». J. Phys. Chem. 113 (1): 19–22. Bibcode:2009JPCA..113 ... 19 Вт. Дои:10.1021 / jp804420g. PMID 19072712.
- ^ Abbott, Benjamin P .; и другие. (Научное сотрудничество LIGO и сотрудничество Девы) (2016). «Наблюдение гравитационно-волнового переходного процесса GW150914 с минимальными допущениями». Phys. Ред. D. 93 (12): 122004. arXiv:1602.03843. Bibcode:2016ПхРвД..93л2004А. Дои:10.1103 / PhysRevD.93.122004.
- ^ В. Некула, С. Клименко, Г. Мицельмахер (2012). «Анализ переходных процессов с помощью быстрого частотно-временного преобразования Вильсона-Добеши». Journal of Physics: Серия конференций. 363: 012032. Дои:10.1088/1742-6596/363/1/012032.
- ^ J. Rafiee et al. Извлечение признаков сигналов ЭМГ предплечья для протезирования, Экспертные системы с приложениями 38 (2011) 4058–67.
- ^ J. Rafiee et al. Female sexual responses using signal processing techniques, The Journal of Sexual Medicine 6 (2009) 3086–96. (pdf)
- ^ Rafiee, J .; Tse, Peter W. (2009). "Use of autocorrelation in wavelet coefficients for fault diagnosis". Механические системы и обработка сигналов. 23 (5): 1554–72. Дои:10.1016/j.ymssp.2009.02.008.
- ^ Набор инструментов Matlab – URL: http://matlab.izmiran.ru/help/toolbox/wavelet/ch06_a32.html
- ^ Erik Hjelmås (1999-01-21) Gabor Wavelets URL: http://www.ansatt.hig.no/erikh/papers/scia99/node6.html
Источники
- Haar A., Zur Theorie der orthogonalen Funktionensysteme, Mathematische Annalen, 69, pp 331–371, 1910.
- Ингрид Добешис, Десять лекций по вейвлетам, Общество промышленной и прикладной математики, 1992 г., ISBN 0-89871-274-2
- Ali Akansu and Richard Haddad, Multiresolution Signal Decomposition: Transforms, Subbands, Wavelets, Academic Press, 1992, ISBN 0-12-047140-X
- P. P. Vaidyanathan, Multirate Systems and Filter Banks, Прентис-Холл, 1993 г., ISBN 0-13-605718-7
- Gerald Kaiser, A Friendly Guide to Wavelets, Birkhauser, 1994, ISBN 0-8176-3711-7
- Mladen Victor Wickerhauser, Adapted Wavelet Analysis From Theory to Software, A K Peters Ltd, 1994, ISBN 1-56881-041-5
- Martin Vetterli and Jelena Kovačević, "Wavelets and Subband Coding", Prentice Hall, 1995, ISBN 0-13-097080-8
- Barbara Burke Hubbard, "The World According to Wavelets: The Story of a Mathematical Technique in the Making", AK Peters Ltd, 1998, ISBN 1-56881-072-5, ISBN 978-1-56881-072-0
- Stéphane Mallat, "A wavelet tour of signal processing" 2nd Edition, Academic Press, 1999, ISBN 0-12-466606-X
- Donald B. Percival and Andrew T. Walden, Wavelet Methods for Time Series Analysis, Cambridge University Press, 2000 г., ISBN 0-521-68508-7
- Ramazan Gençay, Faruk Selçuk and Brandon Whitcher, An Introduction to Wavelets and Other Filtering Methods in Finance and Economics, Academic Press, 2001, г. ISBN 0-12-279670-5
- Paul S. Addison, The Illustrated Wavelet Transform Handbook, Институт Физики, 2002, ISBN 0-7503-0692-0
- B. Boashash, editor, "Time-Frequency Signal Analysis and Processing – A Comprehensive Reference", Elsevier Science, Oxford, 2003, ISBN 0-08-044335-4.
- Тони Ф. Чан и "Jackie (Jianhong) Shen", Image Processing and Analysis – Variational, PDE, Wavelet, and Stochastic Methods, Society of Applied Mathematics, ISBN 0-89871-589-X (2005)
- Нажмите, WH; Теукольский С.А.; Феттерлинг, штат Вашингтон; Фланнери, BP (2007), "Section 13.10. Wavelet Transforms", Числовые рецепты: искусство научных вычислений (3rd ed.), New York: Cambridge University Press, ISBN 978-0-521-88068-8
внешняя ссылка
В этом разделе использование внешняя ссылка может не следовать политикам или рекомендациям Википедии. (Июль 2016) (Узнайте, как и когда удалить этот шаблон сообщения) |
- Wavelet Digest
- Wavelets: Software – a list of useful wavelet transform frameworks, libraries, and other software
- "Wavelet analysis", Энциклопедия математики, EMS Press, 2001 [1994]
- 1st NJIT Symposium on Wavelets (April 30, 1990) (First Wavelets Conference in USA)
- Binomial-QMF Daubechies Wavelets
- Wavelets by Gilbert Strang, American Scientist 82 (1994) 250–255. (A very short and excellent introduction)
- Course on Wavelets given at UC Santa Barbara, 2004
- Wavelets for Kids (PDF file) (Introductory (for very smart kids!))
- WITS: Where Is The Starlet? A dictionary of tens of wavelets and wavelet-related terms ending in -let, from activelets to x-lets through bandlets, contourlets, curvelets, noiselets, wedgelets.
- The Fractional Spline Wavelet Transform описывает fractional wavelet transform based on fractional b-Splines.
- A Panorama on Multiscale Geometric Representations, Intertwining Spatial, Directional and Frequency Selectivity provides a tutorial on two-dimensional oriented wavelets and related geometric multiscale transforms.
- Signal Denoising using Wavelets
- Concise Introduction to Wavelets by René Puschinger