Квантование (обработка сигналов) - Quantization (signal processing)

Самый простой способ квантовать сигнал - выбрать значение цифровой амплитуды, наиболее близкое к исходной аналоговой амплитуде. В этом примере показан исходный аналоговый сигнал (зеленый), квантованный сигнал (черные точки), сигнал реконструирован от квантованного сигнала (желтый) и разницы между исходным сигналом и восстановленным сигналом (красный). Разница между исходным сигналом и восстановленным сигналом является ошибкой квантования и, в этой простой схеме квантования, является детерминированной функцией входного сигнала.

Квантование, по математике и цифровая обработка сигналов, представляет собой процесс отображения входных значений из большого набора (часто непрерывного набора) в выходные значения в (счетном) меньшем наборе, часто с конечным количество элементов. Округление и усечение являются типичными примерами процессов квантования. Квантование в некоторой степени участвует почти во всей цифровой обработке сигналов, поскольку процесс представления сигнала в цифровой форме обычно включает округление. Квантование также составляет основу практически всех сжатие с потерями алгоритмы.

Разница между входным значением и его квантованным значением (например, ошибка округления ) упоминается как ошибка квантования. Устройство или алгоритмическая функция который выполняет квантование, называется квантователь. An аналого-цифровой преобразователь является примером квантователя.

Пример

В качестве примера, округление а настоящий номер ${\displaystyle x}$ до ближайшего целого числа образует очень простой тип квантователя - униформа один. Типичный (середина протектора) равномерный квантователь с квантованием размер шага равно некоторому значению ${\displaystyle \Delta }$ можно выразить как

${\displaystyle Q(x)=\Delta \cdot \left\lfloor {\frac {x}{\Delta }}+{\frac {1}{2}}\right\rfloor }$,

где обозначение ${\displaystyle \lfloor \ \rfloor }$ обозначает функция пола.

Существенным свойством квантователя является то, что он имеет счетный набор возможных выходных значений, который имеет меньше членов, чем набор возможных входных значений. Члены набора выходных значений могут иметь целые, рациональные или действительные значения. Для простого округления до ближайшего целого числа размер шага ${\displaystyle \Delta }$ равно 1. С ${\displaystyle \Delta =1}$ или с ${\displaystyle \Delta }$ Как и любое другое целочисленное значение, этот квантователь имеет действительные входные и целочисленные выходы.

Когда размер шага квантования (Δ) невелик по сравнению с изменением квантованного сигнала, относительно просто показать, что среднеквадратичная ошибка произведенное такой операцией округления будет приблизительно ${\displaystyle \Delta ^{2}/12}$.^{[1][2][3][4][5][6]} Среднеквадратичная ошибка также называется квантованием. мощность шума. Добавление одного бита к квантователю уменьшает вдвое значение Δ, что снижает мощность шума в раз. С точки зрения децибелы, изменение мощности шума равно ${\displaystyle \scriptstyle 10\cdot \log _{10}(1/4)\ \approx \ -6\ \mathrm {dB} .}$

Поскольку набор возможных выходных значений квантователя является счетным, любой квантователь можно разложить на два отдельных этапа, которые можно назвать классификация этап (или прямое квантование этап) и реконструкция этап (или обратное квантование stage), где на этапе классификации входное значение преобразуется в целое число индекс квантования ${\displaystyle k}$ а этап реконструкции отображает индекс ${\displaystyle k}$ к стоимость реконструкции ${\displaystyle y_{k}}$ это выходное приближение входного значения. Для примера равномерного квантователя, описанного выше, этап прямого квантования может быть выражен как

${\displaystyle k=\left\lfloor {\frac {x}{\Delta }}+{\frac {1}{2}}\right\rfloor }$,

и этап восстановления для этого примера квантователя просто

${\displaystyle y_{k}=k\cdot \Delta }$.

Это разложение полезно для разработки и анализа поведения квантования, и оно показывает, как квантованные данные могут быть переданы по каналу связи - кодировщик источника может выполнять этап прямого квантования и отправлять индексную информацию по каналу связи, а декодер может выполнять этап реконструкции для получения выходного приближения исходных входных данных. В общем, на этапе прямого квантования может использоваться любая функция, которая отображает входные данные в целочисленное пространство данных индекса квантования, а этап обратного квантования может концептуально (или буквально) быть операцией просмотра таблицы для отображения каждого индекса квантования на соответствующее значение реконструкции. Это двухэтапное разложение одинаково хорошо применимо к вектор а также скалярные квантователи.

Математические свойства

Поскольку квантование - это отображение "многие-к-немногим", оно по своей сути нелинейный и необратимый процесс (то есть, поскольку одно и то же выходное значение используется несколькими входными значениями, в общем случае невозможно восстановить точное входное значение, если задано только выходное значение).

Набор возможных входных значений может быть бесконечно большим и, возможно, непрерывным и, следовательно, бесчисленный (например, набор всех действительные числа, или все действительные числа в некотором ограниченном диапазоне). Набор возможных выходных значений может быть конечный или же счетно бесконечный.^[6] Наборы входов и выходов, участвующие в квантовании, можно определить довольно общим образом. Например, векторное квантование представляет собой приложение квантования к многомерным (векторным) входным данным.^[7]

Типы

2-битное разрешение с четырьмя уровнями квантования по сравнению с аналоговым.^[8]

3-битное разрешение с восемью уровнями.

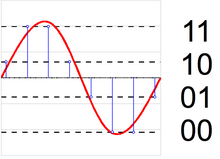
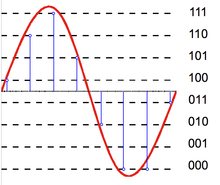
Аналого-цифровой преобразователь

An аналого-цифровой преобразователь (ADC) можно смоделировать как два процесса: отбор проб и квантование. Выборка преобразует изменяющийся во времени сигнал напряжения в сигнал с дискретным временем, последовательность действительные числа. Квантование заменяет каждое действительное число приближением из конечного набора дискретных значений. Чаще всего эти дискретные значения представлены в виде слов с фиксированной точкой. Хотя возможно любое количество уровней квантования, общая длина слова 8 бит (256 уровней), 16 бит (65 536 уровней) и 24 бит (16,8 млн уровней). Квантование последовательности чисел дает последовательность ошибок квантования, которая иногда моделируется как аддитивный случайный сигнал, называемый шум квантования из-за его стохастический поведение. Чем больше уровней использует квантователь, тем ниже его мощность шума квантования.

Оптимизация скорости и искажений

Оптимизированный коэффициент искажения квантование встречается в исходное кодирование для алгоритмов сжатия данных с потерями, целью которых является управление искажением в пределах скорости передачи данных, поддерживаемой каналом связи или носителем данных. Анализ квантования в этом контексте включает изучение количества данных (обычно измеряемых цифрами, битами или битами). ставка), который используется для представления выходных данных квантователя, и изучения потери точности, вызванной процессом квантования (который называется искажение).

Унифицированные квантователи со средней подступенкой и средней ступенью

Большинство однородных квантователей для входных данных со знаком можно разделить на два типа: средний человек и середина протектора. Терминология основана на том, что происходит в области вокруг значения 0, и использует аналогию с просмотром функции ввода-вывода квантователя как лестница. Квантователи среднего протектора имеют нулевой уровень реконструкции (соответствующий ступать лестницы), в то время как квантователи средней ступени имеют нулевой порог классификации (соответствующий стояк лестницы).^[9]

Квантование середины протектора предполагает округление. Формулы для равномерного квантования средней протектора приведены в предыдущем разделе.

Квантование среднего уровня включает усечение. Формула ввода-вывода для равномерного квантователя среднего уровня определяется следующим образом:

${\displaystyle Q(x)=\Delta \cdot \left(\left\lfloor {\frac {x}{\Delta }}\right\rfloor +{\frac {1}{2}}\right)}$,

где правило классификации дается

${\displaystyle k=\left\lfloor {\frac {x}{\Delta }}\right\rfloor }$

и правило реконструкции

${\displaystyle y_{k}=\Delta \cdot \left(k+{\tfrac {1}{2}}\right)}$.

Обратите внимание, что унифицированные квантователи среднего уровня не имеют нулевого выходного значения - их минимальная выходная величина составляет половину размера шага. В отличие от этого, квантователи со средним протектором имеют нулевой выходной уровень. Для некоторых приложений может потребоваться представление нулевого выходного сигнала.

В общем, квантователь со средним подступенком или средним протектором на самом деле не может быть униформа квантователь - то есть размер интервалов классификации квантователя может не быть одинаковым, или интервалы между его возможными выходными значениями могут не быть одинаковыми. Отличительной особенностью квантователя среднего уровня является то, что он имеет значение порога классификации, которое точно равно нулю, а отличительная характеристика квантователя среднего уровня состоит в том, что он имеет значение восстановления, которое точно равно нулю.^[9]

Квантователи мертвой зоны

А квантователь мертвой зоны - это тип квантователя среднего уровня с симметричным поведением около 0. Область вокруг нулевого выходного значения такого квантователя называется мертвая зона или же зона нечувствительности. Мертвая зона иногда может служить той же цели, что и шумовые ворота или же хлюпать функция. В частности, для компрессионных приложений ширина мертвой зоны может отличаться от ширины других ступеней. Для однородного квантователя ширина мертвой зоны может быть установлена ​​на любое значение. ${\displaystyle w}$ с помощью правила прямого квантования^[10][11][12]

${\displaystyle k=\operatorname {sgn}(x)\cdot \max \left(0,\left\lfloor {\frac {\left|x\right|-w/2}{\Delta }}+1\right\rfloor \right)}$,

где функция ${\displaystyle \operatorname {sgn} }$( ) это функция знака (также известный как сигнум функция). Общее правило реконструкции для такого квантователя мертвой зоны дается формулой

${\displaystyle y_{k}=\operatorname {sgn}(k)\cdot \left({\frac {w}{2}}+\Delta \cdot (|k|-1+r_{k})\right)}$,

куда ${\displaystyle r_{k}}$ - значение смещения реконструкции в диапазоне от 0 до 1 как часть размера шага. Обычно ${\displaystyle 0\leq r_{k}\leq {\tfrac {1}{2}}}$ при квантовании входных данных с типичным функция плотности вероятности (pdf), который симметричен относительно нуля и достигает максимального значения при нуле (например, Гауссовский, Лапласиан, или же обобщенный гауссовский pdf). Несмотря на то что ${\displaystyle r_{k}}$ может зависеть от ${\displaystyle k}$ в общем, и может быть выбран для выполнения условия оптимальности, описанного ниже, часто просто устанавливается на константу, например ${\displaystyle {\tfrac {1}{2}}}$. (Обратите внимание, что в этом определении ${\displaystyle y_{0}=0}$ из-за определения ${\displaystyle \operatorname {sgn} }$( ) функция, поэтому ${\displaystyle r_{0}}$ не имеет никакого эффекта.)

Очень часто используемый частный случай (например, схема, обычно используемая в финансовом учете и элементарной математике) - это установка ${\displaystyle w=\Delta }$ и ${\displaystyle r_{k}={\tfrac {1}{2}}}$ для всех ${\displaystyle k}$. В этом случае квантователь мертвой зоны также является равномерным квантователем, так как центральная мертвая зона этого квантователя имеет такую ​​же ширину, как и все его другие шаги, и все его значения восстановления также расположены на одинаковом расстоянии.

Характеристики шума и ошибок

Модель аддитивного шума

Распространенное допущение для анализа ошибка квантования в том, что он влияет на систему обработки сигналов аналогично аддитивному белый шум - имеющая пренебрежимо малую корреляцию с сигналом и приблизительно ровную спектральная плотность мощности.^{[2][6][13][14]} Модель аддитивного шума обычно используется для анализа эффектов ошибок квантования в системах цифровой фильтрации и может быть очень полезна в таком анализе. Было показано, что это действительная модель в случаях квантования с высоким разрешением (малые ${\displaystyle \Delta }$ относительно мощности сигнала) с гладкими функциями плотности вероятности.^[2][15]

Аддитивное шумовое поведение не всегда является верным предположением. Ошибка квантования (для квантователей, определенных как описано здесь) детерминированно связана с сигналом и не полностью от него независима. Таким образом, периодические сигналы могут создавать периодический шум квантования. А в некоторых случаях это может даже вызвать предельные циклы появиться в системах цифровой обработки сигналов. Один из способов гарантировать эффективную независимость ошибки квантования от исходного сигнала - выполнить смущенный квантование (иногда с формирование шума ), который включает добавление случайных (или псевдослучайный ) шум к сигналу до квантования.^[6][14]

Модели ошибок квантования

В типичном случае исходный сигнал намного больше одного младший бит (МЗБ). В этом случае ошибка квантования существенно не коррелирует с сигналом и имеет приблизительно равномерное распределение. Когда округление используется для квантования, ошибка квантования имеет иметь в виду нуля и среднеквадратичное значение (RMS) значение - это стандартное отклонение этого распределения, задаваемого ${\displaystyle \scriptstyle {\frac {1}{\sqrt {12}}}\mathrm {LSB} \ \approx \ 0.289\,\mathrm {LSB} }$. Когда используется усечение, ошибка имеет ненулевое среднее значение ${\displaystyle \scriptstyle {\frac {1}{2}}\mathrm {LSB} }$ а значение RMS равно ${\displaystyle \scriptstyle {\frac {1}{\sqrt {3}}}\mathrm {LSB} }$. В любом случае стандартное отклонение, как процент от полного диапазона сигнала, изменяется с коэффициентом 2 для каждого 1-битного изменения числа битов квантования. Следовательно, потенциальное отношение мощности сигнала к мощности шума квантования изменяется на 4 или ${\displaystyle \scriptstyle 10\cdot \log _{10}(4)}$, примерно 6 дБ на бит.

При более низких амплитудах ошибка квантования становится зависимой от входного сигнала, что приводит к искажению. Это искажение создается после сглаживания фильтра, и, если эти искажения превышают 1/2 частоты дискретизации, они возвращаются в интересующую полосу. Чтобы ошибка квантования не зависела от входного сигнала, сигнал смущенный путем добавления шума к сигналу. Это немного снижает отношение сигнал / шум, но может полностью устранить искажения.

Модель шума квантования

Шум квантования для 2-битного АЦП, работающего на бесконечности частота дискретизации. Разница между синим и красным сигналами на верхнем графике - это ошибка квантования, которая «добавляется» к квантованному сигналу и является источником шума.

Сравнение квантования синусоиды на 64 уровня (6 бит) и 256 уровней (8 бит). Аддитивный шум, создаваемый 6-битным квантованием, на 12 дБ больше, чем шум, создаваемый 8-битным квантованием. Когда спектральное распределение ровное, как в этом примере, разница в 12 дБ проявляется как измеримая разница в минимальном уровне шума.

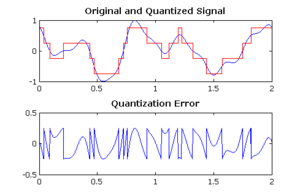
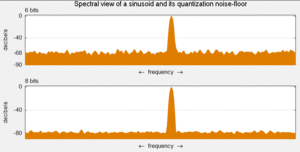
Шум квантования - это модель ошибки квантования, вызванной квантованием в аналого-цифровое преобразование (АЦП). Это ошибка округления между аналоговым входным напряжением АЦП и выходным цифровым значением. Шум нелинейный и зависит от сигнала. Его можно смоделировать несколькими способами.

В идеальном аналого-цифровом преобразователе, где ошибка квантования равномерно распределена между -1/2 LSB и +1/2 LSB, а сигнал имеет равномерное распределение, охватывающее все уровни квантования, Отношение сигнал / шум квантования (SQNR) можно рассчитать из

${\displaystyle \mathrm {SQNR} =20\log _{10}(2^{Q})\approx 6.02\cdot Q\ \mathrm {dB} \,\!}$

где Q - количество битов квантования.

Наиболее распространенные тестовые сигналы, которые соответствуют этому, - это полная амплитуда треугольные волны и пилообразные волны.

Например, 16 бит Максимальное отношение сигнал / шум квантования АЦП составляет 6,02 × 16 = 96,3 дБ.

Когда входной сигнал имеет полную амплитуду синусоидальная волна распределение сигнала больше не является равномерным, и вместо этого соответствующее уравнение

${\displaystyle \mathrm {SQNR} \approx 1.761+6.02\cdot Q\ \mathrm {dB} \,\!}$

Здесь шум квантования снова предполагается быть равномерно распределенным. Это так, когда входной сигнал имеет высокую амплитуду и широкий частотный спектр.^[16] В этом случае 16-битный АЦП имеет максимальное отношение сигнал / шум 98,09 дБ. Разница в соотношении сигнал-шум 1,761 возникает только из-за того, что сигнал представляет собой полномасштабную синусоидальную волну, а не треугольник или пилообразную форму.

Для сложных сигналов в АЦП с высоким разрешением это точная модель. Для АЦП с низким разрешением, сигналов низкого уровня в АЦП с высоким разрешением и для простых сигналов шум квантования распределяется неравномерно, что делает эту модель неточной.^[17] В этих случаях на распределение шума квантования сильно влияет точная амплитуда сигнала.

Вычисления относятся к исходной величине. Для сигналов меньшего размера относительное искажение квантования может быть очень большим. Чтобы обойти эту проблему, аналог компандирование можно использовать, но это может привести к искажению.

Дизайн

Гранулярное искажение и искажение при перегрузке

Часто конструкция квантователя включает поддержку только ограниченного диапазона возможных выходных значений и выполнение отсечения для ограничения выхода этим диапазоном всякий раз, когда входной сигнал превышает поддерживаемый диапазон. Ошибка, вызванная этим отсечением, называется перегрузка искажение. В крайних пределах поддерживаемого диапазона величина интервала между выбираемыми выходными значениями квантователя называется его детализация, и ошибка, вызванная этим интервалом, называется гранулированный искажение. При разработке квантователя обычно используется определение надлежащего баланса между зернистым искажением и искажением из-за перегрузки. Для заданного поддерживаемого числа возможных выходных значений уменьшение среднего гранулярного искажения может включать увеличение среднего искажения от перегрузки, и наоборот. Методика управления амплитудой сигнала (или, что то же самое, размером шага квантования ${\displaystyle \Delta }$) для достижения соответствующего баланса является использование автоматическая регулировка усиления (AGC). Однако в некоторых схемах квантователя концепции гранулярной ошибки и ошибки перегрузки могут не применяться (например, для квантователя с ограниченным диапазоном входных данных или со счетно бесконечным набором выбираемых выходных значений).^[6]

Конструкция квантователя скорости-искажения

Скалярный квантователь, который выполняет операцию квантования, обычно можно разделить на два этапа:

Классификация

Процесс, который классифицирует диапазон входного сигнала на ${\displaystyle M}$ неперекрывающийся интервалы ${\displaystyle \{I_{k}\}_{k=1}^{M}}$, определяя ${\displaystyle M-1}$ граница решения значения ${\displaystyle \{b_{k}\}_{k=1}^{M-1}}$, так что ${\displaystyle I_{k}=[b_{k-1}~,~b_{k})}$ за ${\displaystyle k=1,2,\ldots ,M}$, с крайними пределами, определяемыми ${\displaystyle b_{0}=-\infty }$ и ${\displaystyle b_{M}=\infty }$. Все входы ${\displaystyle x}$ попадают в заданный интервал ${\displaystyle I_{k}}$ связаны с одним и тем же индексом квантования ${\displaystyle k}$.

Реконструкция

Каждый интервал ${\displaystyle I_{k}}$ представлен стоимость реконструкции ${\displaystyle y_{k}}$ который реализует отображение ${\displaystyle x\in I_{k}\Rightarrow y=y_{k}}$.

Эти два этапа вместе составляют математическую операцию ${\displaystyle y=Q(x)}$.

Энтропийное кодирование методы могут применяться для передачи индексов квантования от исходного кодера, который выполняет этап классификации, в декодер, который выполняет этап восстановления. Один из способов сделать это - связать каждый индекс квантования ${\displaystyle k}$ с двоичным кодовым словом ${\displaystyle c_{k}}$. Важным фактором является количество битов, используемых для каждого кодового слова, обозначенное здесь как ${\displaystyle \mathrm {length} (c_{k})}$. В результате дизайн ${\displaystyle M}$квантователь уровня и связанный с ним набор кодовых слов для передачи значений индекса требует нахождения значений ${\displaystyle \{b_{k}\}_{k=1}^{M-1}}$, ${\displaystyle \{c_{k}\}_{k=1}^{M}}$ и ${\displaystyle \{y_{k}\}_{k=1}^{M}}$ которые оптимально удовлетворяют выбранному набору проектных ограничений, таких как битрейт ${\displaystyle R}$ и искажение ${\displaystyle D}$.

Предполагая, что источник информации ${\displaystyle S}$ производит случайные величины ${\displaystyle X}$ с ассоциированным функция плотности вероятности ${\displaystyle f(x)}$вероятность ${\displaystyle p_{k}}$ что случайная величина попадает в определенный интервал квантования ${\displaystyle I_{k}}$ дан кем-то:

${\displaystyle p_{k}=P[x\in I_{k}]=\int _{b_{k-1}}^{b_{k}}f(x)dx}$.

Результирующий битрейт ${\displaystyle R}$в единицах среднего числа битов на квантованное значение для этого квантователя можно получить следующим образом:

${\displaystyle R=\sum _{k=1}^{M}p_{k}\cdot \mathrm {length} (c_{k})=\sum _{k=1}^{M}\mathrm {length} (c_{k})\int _{b_{k-1}}^{b_{k}}f(x)dx}$.

Если предположить, что искажение измеряется среднеквадратичная ошибка,^[а] искажение D, дан кем-то:

${\displaystyle D=E[(x-Q(x))^{2}]=\int _{-\infty }^{\infty }(x-Q(x))^{2}f(x)dx=\sum _{k=1}^{M}\int _{b_{k-1}}^{b_{k}}(x-y_{k})^{2}f(x)dx}$.

Ключевое наблюдение заключается в том, что скорость ${\displaystyle R}$ зависит от границ решения ${\displaystyle \{b_{k}\}_{k=1}^{M-1}}$ и длины кодовых слов ${\displaystyle \{\mathrm {length} (c_{k})\}_{k=1}^{M}}$, а искажение ${\displaystyle D}$ зависит от границ решения ${\displaystyle \{b_{k}\}_{k=1}^{M-1}}$ и уровни реконструкции ${\displaystyle \{y_{k}\}_{k=1}^{M}}$.

После определения этих двух показателей производительности для квантователя, типичная формулировка «скорость – искажение» для задачи разработки квантователя может быть выражена одним из двух способов:

1. Учитывая ограничение максимального искажения ${\displaystyle D\leq D_{\max }}$, минимизировать битрейт ${\displaystyle R}$
2. Учитывая ограничение максимальной скорости передачи данных ${\displaystyle R\leq R_{\max }}$, минимизировать искажение ${\displaystyle D}$

Часто решение этих проблем может быть эквивалентно (или приблизительно) выражено и решено путем преобразования формулировки к неограниченной проблеме ${\displaystyle \min \left\{D+\lambda \cdot R\right\}}$ где Множитель Лагранжа ${\displaystyle \lambda }$ - неотрицательная константа, которая устанавливает соответствующий баланс между скоростью и искажениями. Решение неограниченной задачи эквивалентно нахождению точки на выпуклый корпус семейства решений эквивалентной постановки задачи с ограничениями. Однако поиск решения - особенно закрытая форма Решение - любая из этих трех формулировок проблемы может быть сложной. Решения, не требующие многомерных итерационных методов оптимизации, были опубликованы только для трех функций распределения вероятностей: униформа,^[18] экспоненциальный,^[12] и Лапласиан^[12] раздачи. Подходы итеративной оптимизации могут использоваться для поиска решений в других случаях.^[6][19][20]

Обратите внимание, что значения реконструкции ${\displaystyle \{y_{k}\}_{k=1}^{M}}$ влияют только на искажения - они не влияют на скорость передачи данных - и что каждый в отдельности ${\displaystyle y_{k}}$ делает отдельный вклад ${\displaystyle d_{k}}$ к общему искажению, как показано ниже:

${\displaystyle D=\sum _{k=1}^{M}d_{k}}$

куда

${\displaystyle d_{k}=\int _{b_{k-1}}^{b_{k}}(x-y_{k})^{2}f(x)dx}$

Это наблюдение можно использовать для облегчения анализа - учитывая набор ${\displaystyle \{b_{k}\}_{k=1}^{M-1}}$ ценности, ценность каждого ${\displaystyle y_{k}}$ можно оптимизировать отдельно, чтобы свести к минимуму его вклад в искажение ${\displaystyle D}$.

Для критерия искажения среднеквадратичной ошибки легко показать, что оптимальный набор значений восстановления ${\displaystyle \{y_{k}^{*}\}_{k=1}^{M}}$ задается установкой значения реконструкции ${\displaystyle y_{k}}$ в каждом интервале ${\displaystyle I_{k}}$ к условному ожидаемому значению (также называемому центроид ) в пределах интервала, как указано:

${\displaystyle y_{k}^{*}={\frac {1}{p_{k}}}\int _{b_{k-1}}^{b_{k}}xf(x)dx}$.

Использование достаточно хорошо продуманных методов энтропийного кодирования может привести к использованию скорости передачи данных, близкой к истинному информационному содержанию индексов. ${\displaystyle \{k\}_{k=1}^{M}}$, так что эффективно

${\displaystyle \mathrm {length} (c_{k})\approx -\log _{2}\left(p_{k}\right)}$

и поэтому

${\displaystyle R=\sum _{k=1}^{M}-p_{k}\cdot \log _{2}\left(p_{k}\right)}$.

Использование этого приближения может позволить отделить проблему проектирования энтропийного кодирования от конструкции самого квантователя. Современные методы энтропийного кодирования, такие как арифметическое кодирование может достигать скорости передачи данных, которая очень близка к истинной энтропии источника, учитывая набор известных (или адаптивно оцененных) вероятностей ${\displaystyle \{p_{k}\}_{k=1}^{M}}$.

В некоторых проектах вместо оптимизации для определенного количества областей классификации ${\displaystyle M}$, проблема проектирования квантователя может включать оптимизацию значения ${\displaystyle M}$ также. Для некоторых вероятностных моделей источников наилучшие характеристики могут быть достигнуты, когда ${\displaystyle M}$ приближается к бесконечности.

Пренебрежение ограничением энтропии: квантование Ллойда – Макса

В приведенной выше формулировке, если пренебречь ограничением скорости передачи данных путем установки ${\displaystyle \lambda }$ равным 0, или, что эквивалентно, если предполагается, что код фиксированной длины (FLC) будет использоваться для представления квантованных данных вместо код переменной длины (или какой-либо другой технологии энтропийного кодирования, такой как арифметическое кодирование, которое лучше, чем FLC в смысле скорость – искажение), проблема оптимизации сводится к минимизации искажений ${\displaystyle D}$ один.

Индексы, производимые ${\displaystyle M}$квантователь уровня может быть закодирован с использованием кода фиксированной длины, используя ${\displaystyle R=\lceil \log _{2}M\rceil }$ бит / символ. Например, когда ${\displaystyle M=}$256 уровней, битрейт FLC ${\displaystyle R}$ составляет 8 бит / символ. По этой причине такой квантователь иногда называют 8-битным квантователем. Однако использование FLC устраняет улучшение сжатия, которое может быть получено за счет использования лучшего энтропийного кодирования.

Предполагая, что FLC с ${\displaystyle M}$ уровней, проблема минимизации искажений может быть сведена только к минимизации искажений. Редуцированная задача может быть сформулирована следующим образом: с учетом источника ${\displaystyle X}$ с pdf ${\displaystyle f(x)}$ и ограничение, которое квантователь должен использовать только ${\displaystyle M}$ классификации регионов, найти границы решения ${\displaystyle \{b_{k}\}_{k=1}^{M-1}}$ и уровни реконструкции ${\displaystyle \{y_{k}\}_{k=1}^{M}}$ минимизировать результирующие искажения

${\displaystyle D=E[(x-Q(x))^{2}]=\int _{-\infty }^{\infty }(x-Q(x))^{2}f(x)dx=\sum _{k=1}^{M}\int _{b_{k-1}}^{b_{k}}(x-y_{k})^{2}f(x)dx=\sum _{k=1}^{M}d_{k}}$.

Нахождение оптимального решения вышеуказанной проблемы приводит к квантователю, который иногда называют решением MMSQE (минимальная среднеквадратическая ошибка квантования), а полученный в результате оптимизированный для pdf (неоднородный) квантователь называется Ллойд – Макс квантователь, названный в честь двух людей, которые независимо разработали итерационные методы^[6][21][22] для решения двух систем одновременных уравнений в результате ${\displaystyle {\partial D/\partial b_{k}}=0}$ и ${\displaystyle {\partial D/\partial y_{k}}=0}$, следующее:

${\displaystyle {\partial D \over \partial b_{k}}=0\Rightarrow b_{k}={y_{k}+y_{k+1} \over 2}}$,

который помещает каждый порог в середину между каждой парой значений реконструкции, и

${\displaystyle {\partial D \over \partial y_{k}}=0\Rightarrow y_{k}={\int _{b_{k-1}}^{b_{k}}xf(x)dx \over \int _{b_{k-1}}^{b_{k}}f(x)dx}={\frac {1}{p_{k}}}\int _{b_{k-1}}^{b_{k}}xf(x)dx}$

который помещает каждое значение реконструкции в центроид (условное ожидаемое значение) соответствующего интервала классификации.

Алгоритм метода Ллойда I, первоначально описанный в 1957 году, может быть просто обобщен для применения в вектор данные. Это обобщение приводит к Линде – Бузо – Грей (LBG) или же k-означает методы оптимизации классификатора. Кроме того, метод может быть дополнительно обобщен прямым способом, чтобы также включить ограничение энтропии для векторных данных.^[23]

Равномерное квантование и приближение 6 дБ / бит

Квантователь Ллойда – Макса на самом деле является равномерным квантователем, когда входной PDF-файл равномерно распределен по диапазону ${\displaystyle [y_{1}-\Delta /2,~y_{M}+\Delta /2)}$. Однако для источника, который не имеет равномерного распределения, квантователь с минимальным искажением не может быть равномерным квантователем. Анализ равномерного квантователя, примененного к равномерно распределенному источнику, можно резюмировать следующим образом:

Симметричный источник X можно смоделировать с помощью ${\displaystyle f(x)={\tfrac {1}{2X_{\max }}}}$, за ${\displaystyle x\in [-X_{\max },X_{\max }]}$ и 0 в другом месте. ${\displaystyle \Delta ={\tfrac {2X_{\max }}{M}}}$ и отношение сигнал / шум квантования (SQNR) квантователя равно

${\displaystyle {\rm {SQNR}}=10\log _{10}{\frac {\sigma _{x}^{2}}{\sigma _{q}^{2}}}=10\log _{10}{\frac {(M\Delta )^{2}/12}{\Delta ^{2}/12}}=10\log _{10}M^{2}=20\log _{10}M}$.

Для кода фиксированной длины с использованием ${\displaystyle N}$ биты ${\displaystyle M=2^{N}}$, в результате чего${\displaystyle {\rm {SQNR}}=20\log _{10}{2^{N}}=N\cdot (20\log _{10}2)=N\cdot 6.0206\,{\rm {dB}}}$,

или примерно 6 дБ на бит. Например, для ${\displaystyle N}$= 8 бит, ${\displaystyle M}$= 256 уровней и SQNR = 8 × 6 = 48 дБ; и для ${\displaystyle N}$= 16 бит, ${\displaystyle M}$= 65536 и SQNR = 16 × 6 = 96 дБ. Свойство улучшения SQNR на 6 дБ для каждого дополнительного бита, используемого при квантовании, является хорошо известным показателем качества. Однако его следует использовать с осторожностью: этот вывод предназначен только для равномерного квантователя, применяемого к однородному источнику. Для других исходных PDF-файлов и других конструкций квантователя SQNR может несколько отличаться от прогнозируемого на 6 дБ / бит, в зависимости от типа PDF-файла, типа источника, типа квантователя и рабочего диапазона битовой скорости.

Однако обычно предполагается, что для многих источников наклон функции SQNR квантователя может быть аппроксимирован как 6 дБ / бит при работе с достаточно высокой скоростью передачи данных. При асимптотически высоких скоростях передачи данных уменьшение размера шага вдвое увеличивает скорость передачи данных примерно на 1 бит на выборку (поскольку 1 бит необходим, чтобы указать, находится ли значение в левой или правой половине предыдущего интервала двойного размера) и уменьшает среднеквадратичная ошибка в 4 раза (т. е. 6 дБ) на основе ${\displaystyle \Delta ^{2}/12}$ приближение.

При асимптотически высоких скоростях передачи данных приближение 6 дБ / бит для многих исходных файлов PDF поддерживается строгим теоретическим анализом.^[2][3][5][6] Более того, структура оптимального скалярного квантователя (в смысле «скорость – искажение») приближается к структуре равномерного квантователя в этих условиях.^[5][6]

В других сферах

Смотрите также: Квантовый шум и Квантовый предел

Многие физические величины фактически квантуются физическими объектами. Примеры полей, в которых применяется это ограничение, включают электроника (из-за электроны ), оптика (из-за фотоны ), биология (из-за ДНК ), физика (из-за Пределы Планка ) и химия (из-за молекулы ).

Смотрите также

• Аналого-цифровой преобразователь
• Бета-кодировщик
• Цветовое квантование
• Биннинг данных
• Дискретность
• Ошибка дискретизации
• Квантование (обработка изображений)
• Постеризация
• Импульсно-кодовая модуляция
• Квантиль
• Разбавление регрессии - смещение в оценках параметров, вызванное такими ошибками, как квантование в объясняющей или независимой переменной

Примечания

1. Можно также рассмотреть другие меры искажения, хотя среднеквадратичная ошибка является популярной.

Рекомендации

1. Уильям Флитвуд Шеппард, «О вычислении наиболее вероятных значений частотных постоянных для данных, упорядоченных по равноудаленным делениям шкалы», Труды Лондонского математического общества, Vol. 29, стр. 353–80, 1898.Дои:10.1112 / плмс / с1-29.1.353
2. В. Р. Беннетт "Спектры квантованных сигналов ", Технический журнал Bell System, Vol. 27, стр. 446–472, июль 1948 г.
3. Б. М. Оливер, Дж. Р. Пирс и Клод Э. Шеннон, «Философия ПКМ», Труды IRE, Vol. 36, стр. 1324–1331, ноябрь 1948 г. Дои:10.1109 / JRPROC.1948.231941
4. Сеймур Штайн и Джей Джей Джонс, Принципы современной коммуникации, Макгроу – Хилл, ISBN  978-0-07-061003-3, 1967 (с. 196).
5. Герберт Гиш и Джон Н. Пирс, «Асимптотически эффективное квантование», IEEE Transactions по теории информации, Vol. ИТ-14, № 5, с. 676–683, сентябрь 1968 г. Дои:10.1109 / TIT.1968.1054193
6. Роберт М. Грей и Дэвид Л. Нойхофф, «Квантование», IEEE Transactions по теории информации, Vol. ИТ-44, № 6, стр. 2325–2383, октябрь 1998 г. Дои:10.1109/18.720541
7. Аллен Гершо; Роберт М. Грей (1991). Векторное квантование и сжатие сигналов. Springer. ISBN  978-0-7923-9181-4.
8. Ходжсон, Джей (2010). Понимание записей, стр.56. ISBN  978-1-4411-5607-5. По материалам Franz, David (2004). Запись и продюсирование в домашней студии, стр.38-9. Berklee Press.
9. Аллен Гершо, «Квантование», Журнал IEEE Communications Society, стр. 16–28, сентябрь 1977 г. Дои:10.1109 / MCOM.1977.1089500
10. Раббани, Маджид; Джоши, Раджан Л .; Джонс, Пол В. (2009). «Раздел 1.2.3: Квантование в главе 1: Базовая система кодирования JPEG 2000 (Часть 1)». В Шелкенах, Питер; Скодрас, Афанасий; Эбрахими, Турадж (ред.). Пакет JPEG 2000. Джон Уайли и сыновья. стр.22 –24. ISBN  978-0-470-72147-6.
11. Таубман, Дэвид С .; Марселлин, Майкл В. (2002). «Глава 3: Квантование». JPEG2000: основы, стандарты и практика сжатия изображений. Kluwer Academic Publishers. п.107. ISBN  0-7923-7519-X.
12. Гэри Дж. Салливан, "Эффективное скалярное квантование экспоненциальных и лапласовских случайных величин", IEEE Transactions по теории информации, Vol. ИТ-42, № 5, с. 1365–1374, сентябрь 1996 г. Дои:10.1109/18.532878
13. Бернард Видроу, "Исследование грубого квантования амплитуды с помощью теории дискретизации Найквиста", IRE Trans. Теория схем, Vol. СТ-3, стр. 266–276, 1956. Дои:10.1109 / TCT.1956.1086334
14. Бернард Видроу, "Статистический анализ систем амплитудно-квантованных выборочных данных ", Пер. AIEE Pt. II: Прил. Ind., Vol. 79, стр. 555–568, январь 1961.
15. Даниэль Марко и Дэвид Л. Нойхофф, "Достоверность модели аддитивного шума для однородных скалярных квантователей", IEEE Transactions по теории информации, Vol. ИТ-51, № 5, с. 1739–1755, май 2005 г. Дои:10.1109 / TIT.2005.846397
16. Полман, Кен С. (1989). Принципы цифрового аудио 2-е издание. САМС. п. 60. ISBN  9780071441568.
17. Уоткинсон, Джон (2001). Искусство цифрового аудио, третье издание. Focal Press. ISBN  0-240-51587-0.
18. Нариман Фарвардин и Джеймс В. Модестино, "Оптимальная производительность квантователя для класса негауссовских источников памяти", IEEE Transactions по теории информации, Vol. IT-30, № 3, стр. 485–497, май 1982 г. (Раздел VI.C и Приложение B). Дои:10.1109 / TIT.1984.1056920
19. Тоби Бергер, "Оптимальные квантователи и коды перестановок", IEEE Transactions по теории информации, Vol. ИТ-18, № 6, с. 759–765, ноябрь 1972 г. Дои:10.1109 / TIT.1972.1054906
20. Тоби Бергер, "Квантователи минимальной энтропии и коды перестановок", IEEE Transactions по теории информации, Vol. ИТ-28, № 2, с. 149–157, март 1982 г. Дои:10.1109 / TIT.1982.1056456
21. Стюарт П. Ллойд, «Квантование методом наименьших квадратов в PCM», IEEE Transactions по теории информации, Vol. ИТ-28, с. 129–137, № 2, март 1982 г. Дои:10.1109 / TIT.1982.1056489 (работа задокументирована в рукописи, распространенной для комментариев по адресу Bell Laboratories с датой журнала отдела от 31 июля 1957 г., а также представленной на собрании 1957 г. Институт математической статистики, хотя официально не публиковались до 1982 г.).
22. Джоэл Макс, «Квантование для минимального искажения», Сделки IRE по теории информации, Vol. ИТ-6, стр. 7–12, март 1960 г. Дои:10.1109 / TIT.1960.1057548
23. Филип А. Чоу, Том Лукабо и Роберт М. Грей, "Векторное квантование с ограничениями по энтропии", Транзакции IEEE по акустике, речи и обработке сигналов, Vol. АССП-37, № 1, январь 1989 г. Дои:10.1109/29.17498

• Сайуд, Халид (2005), Введение в сжатие данных, третье издание, Морган Кауфманн, ISBN  978-0-12-620862-7
• Джаянт, Никил С .; Нолл, Питер (1984), Цифровое кодирование сигналов: принципы и приложения к речи и видео, Прентис – Холл, ISBN  978-0-13-211913-9
• Грегг, В. Дэвид (1977), Аналоговая и цифровая связь, Джон Вили, ISBN  978-0-471-32661-8
• Штейн, Сеймур; Джонс, Дж. Джей (1967), Принципы современной коммуникации, Макгроу – Хилл, ISBN  978-0-07-061003-3

внешняя ссылка

• Шум квантования в цифровых вычислениях, обработке сигналов и управлении, Бернард Видроу и Иштван Коллар, 2007.
• Связь динамического диапазона с размером слова данных при обработке цифрового звука
• Дисперсия ошибки округления - вывод мощности шума ${\displaystyle \Delta ^{2}/12}$ для ошибки округления
• Динамическая оценка высокоскоростных цифро-аналоговых преобразователей высокого разрешения Обрисовывает в общих чертах измерения HD, IMD и NPR, также включает вывод шума квантования
• Сигнал к шуму квантования в квантованной синусоидальной