Передискретизация - Upsampling
В цифровая обработка сигналов, повышающая дискретизация, расширение, и интерполяция термины, связанные с процессом повторная выборка в многоскоростная цифровая обработка сигналов система. Передискретизация может быть синонимом расширение, или может описать весь процесс расширение и фильтрация (интерполяция).[1][2][3] Когда повышающая дискретизация выполняется на последовательности выборок сигнал или другой непрерывной функции, он производит приближение последовательности, которая была бы получена путем дискретизации сигнала с более высокой частотой (или плотность, как и в случае с фотографией). Например, если компакт-диск аудио со скоростью 44 100 выборок в секунду повышается с коэффициентом 5/4, результирующая частота дискретизации составляет 55 125.
Повышение дискретизации на целочисленный коэффициент
Увеличение ставки на целочисленный коэффициент L можно объяснить как двухэтапный процесс с эквивалентной более эффективной реализацией.:[4]
- Расширение: создайте последовательность, , включающий оригинальные образцы, разделены по L - 1 нули. Обозначения для этой операции:
- Интерполяция: сгладьте неоднородности с помощью фильтр нижних частот, который заменяет нули.
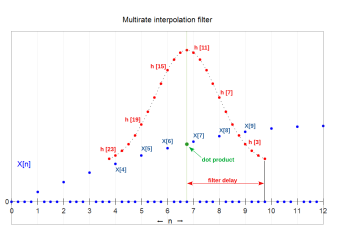
В этом приложении фильтр называется интерполяционный фильтр, а его конструкция обсуждается ниже. Когда фильтр интерполяции FIR типа, его эффективность может быть улучшена, потому что нули ничего не вносят в его скалярное произведение расчеты. Их легко исключить как из потока данных, так и из расчетов. Расчет, выполняемый многоскоростным интерполяционным КИХ-фильтром для каждой выходной выборки, представляет собой скалярное произведение:[а][A]
- и для любого
(Уравнение 1)
где час[•] последовательность - это импульсная характеристика, а K это наибольшее значение k для которого час[j + kL] не равно нулю. В этом случае L = 2, час[•] может быть разработан как полуполосный фильтр, где почти половина коэффициентов равна нулю и их не нужно включать в скалярные произведения. Коэффициенты импульсной характеристики, взятые с интервалом L образуют подпоследовательность, и есть L такие подпоследовательности (называемые фазы) мультиплексированы вместе. Каждый из L фаз импульсной характеристики фильтрует одинаковые последовательные значения Икс[•] поток данных и создание одного из L последовательные выходные значения. В некоторых многопроцессорных архитектурах эти скалярные произведения выполняются одновременно, и в этом случае это называется многофазный фильтр.
Для полноты картины упомянем, что возможная, но маловероятная реализация каждой фазы заключается в замене коэффициентов других фаз нулями в копии час[•] массив и обработать последовательность в L раз быстрее, чем исходная скорость ввода. потом L-1 каждого L выходы равны нулю. Желаемый у[•] последовательность - это сумма фаз, где L-1 члены каждой суммы тождественно равны нулю. Вычисление L-1 нули между полезными выходными сигналами фазы и добавлением их к сумме фактически являются прореживанием. Это тот же результат, что и их совсем не вычислять. Эта эквивалентность известна как вторая Благородная личность.[5] Иногда его используют при выводе многофазного метода.
Дизайн интерполяционного фильтра

Позволять Икс(ж) быть преобразование Фурье любой функции, Икс(т), выборки которой на некотором интервале Т, равно Икс[п] последовательность. Тогда преобразование Фурье с дискретным временем (DTFT) Икс[п] последовательность Ряд Фурье представление периодическое суммирование из Икс(ж):[b]
(Уравнение 2)
Когда Т имеет единицы секунд, имеет единицы герц (Гц). Отбор проб L раз быстрее (с интервалом Т/L) увеличивает периодичность в L:[c]
(Уравнение 3)
что также является желаемым результат интерполяции. Пример обоих этих распределений изображен на первом и третьем графиках фиг.2.
Когда в дополнительные выборки вставляются нули, они увеличивают скорость передачи данных, но они не влияют на распределение частот до тех пор, пока нули не будут заменены интерполяционным фильтром, изображенным на втором графике. Его применение делает первые два графика похожими на третий. Его пропускная способность - это Частота Найквиста исходной последовательности x [n].[B] В единицах Гц это значение но приложения для проектирования фильтров обычно требуют нормализованные единицы. (см. таблицу на рис. 2)
Повышение дискретизации по дробному коэффициенту
Позволять L/M обозначают коэффициент передискретизации, где L > M.
- Превышение выборки в раз L
- Даунсэмпл в разы M
Для повышения частоты дискретизации требуется фильтр нижних частот после увеличения скорости передачи данных, а для понижающей дискретизации требуется фильтр нижних частот перед децимацией. Следовательно, обе операции могут выполняться одним фильтром с более низкой из двух частот среза. Для L > M случае, отсечка интерполяционного фильтра, циклов на промежуточный образец, - нижняя частота.
Смотрите также
- Даунсэмплинг
- Многоскоростная цифровая обработка сигналов
- Полуполосный фильтр
- Передискретизация
- Выборка (теория информации)
- Сигнал (теория информации)
- Конверсия данных
- Интерполяция
- Формула суммирования Пуассона
Примечания
- ^ Выходная последовательность интерполяционного фильтра определяется сверткой:
- ^ Реализуемые фильтры нижних частот имеют "юбку", где отклик уменьшается от почти единицы до почти нуля. Таким образом, на практике частота среза располагается достаточно далеко ниже теоретической среза, чтобы юбка фильтра находилась ниже теоретической среза.
Цитирование страниц
- ^ Крошер и Рабинер «2.3». стр. 38. уравн. 2.80, где что также требует и
- ^ f.harris 2004. «2.2». стр. 23. рис. 2.12 (вверху).
- ^ f.harris 2004. «2.2». стр. 23. рис. 2.12 (внизу).
Рекомендации
- ^ Оппенгейм, Алан В.; Шафер, Рональд У .; Бак, Джон Р. (1999). «4.6.2». Обработка сигналов в дискретном времени (2-е изд.). Река Аппер Сэдл, Нью-Джерси: Prentice Hall. п. 172. ISBN 0-13-754920-2. Также доступно на https://d1.amobbs.com/bbs_upload782111/files_24/ourdev_523225.pdf
- ^ Crochiere, R.E .; Рабинер, Л. (1983). «2.3». Многоскоростная цифровая обработка сигналов. Энглвуд Клиффс, Нью-Джерси: Прентис-Холл. С. 35–36. ISBN 0136051626.
- ^ Пуларикас, Александр Д. (сентябрь 1998 г.). Справочник формул и таблиц для обработки сигналов (1-е изд.). CRC Press. С. 42–48. ISBN 0849385792.
- ^ Харрис, Фредерик Дж. (24 мая 2004 г.). «2.2». Многоскоростная обработка сигналов для систем связи. Река Аппер Сэдл, Нью-Джерси: Prentice Hall PTR. С. 20–21. ISBN 0131465112.
Процесс увеличения выборки можно представить в виде двухэтапной последовательности. Процесс начинается с увеличения частоты дискретизации входной серии x (n) за счет повторной записи [расширения]. Временные ряды с нулевой упаковкой обрабатываются фильтром h (n). В действительности процессы увеличения частоты дискретизации и уменьшения полосы пропускания объединены в один процесс, называемый многоскоростным фильтром.
- ^ Стрэнг, Гилберт; Нгуен, Чыонг (1996-10-01). Вейвлеты и банки фильтров (2-е изд.). Уэллсли, Массачусетс: Wellesley-Cambridge Press. п.101. ISBN 0961408871.
Благородные идентификаторы применяются к каждому многофазному компоненту ... они не применяются ко всему фильтру.
дальнейшее чтение
- Тан, Ли (21 апреля 2008 г.). "Повышение и понижающая дискретизация". eetimes.com. EE Times. Получено 2017-04-10.
- "Домашняя страница передискретизации цифрового аудио". (обсуждает метод интерполяции с ограничением полосы частот)
- "Пример использования многофазных фильтров в Matlab для интерполяции".

![{ displaystyle x_ {L} [n],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d01ee6986d998c5bbbf6c29bc835b7bdd6089d6b)
![{ Displaystyle х [п],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5e286f372d35a48fc88332f573f2902beb862047)
![{ displaystyle x_ {L} [n] = x [n] _ { uparrow L}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a6f8e959ad899e6c64d9ad95bbea1e9e86ae9144)
![{ Displaystyle у [J + NL] = сумма _ {К = 0} ^ {К} х [NK] CDOT H [J + KL], J = 0,1, ldots, L-1, }](https://wikimedia.org/api/rest_v1/media/math/render/svg/7da35f9a584e9e41e8405a5319ab151a2cf3b48f)

![{ Displaystyle scriptstyle x_ {L} [п]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/875f2f50d3e4dc805d8825e6426602c9d87ca1b2)
![{ displaystyle underbrace { sum _ {n = - infty} ^ { infty} overbrace {x (nT)} ^ {x [n]} e ^ {- i2 pi fnT}} _ { текст {DTFT}} = { frac {1} {T}} sum _ {k = - infty} ^ { infty} X { Bigl (} f - { frac {k} {T}} { Bigr)}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e28e17a863ea21733a4861fd9a4ff11435de3804)




![{ displaystyle y [m] = sum _ {r = - infty} ^ { infty} x_ {L} [m-r] cdot h [r]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e3089f9c46818125f2e95e4cedf8f6c1b7902876)
![{ displaystyle x_ {L} [м-р]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5007ccc3012142609f4346e85a32bb1906767d9c)




![{ displaystyle { begin {align} y [m] & = sum _ {k = - infty} ^ { infty} x_ {L} left [{ bigl lfloor} { tfrac {m} { L}} { bigr rfloor} L-kL right] cdot h { Bigl [} overbrace {m - { bigl lfloor} { tfrac {m} {L}} { bigr rfloor} L + kL} ^ {r} { Bigr]} & = sum _ {k = - infty} ^ { infty} x left [{ bigl lfloor} { tfrac {m} {L }} { bigr rfloor} -k right] cdot h left [m - { bigl lfloor} { tfrac {m} {L}} { bigr rfloor} L + kL right] четырехъядерный { stackrel {м треугольник j + nL} { longrightarrow}} четырехъядерный y [j + nL] = sum _ {k = 0} ^ {K} x [nk] cdot h [j + kL], j = 0,1, ldots, L-1 quad { mathsf {(Eq.1)}} end {align}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/851ca95b4b9ce75f0ecec440cd8499a4fee8cecc)


