Округление - Rounding

Графики результата, у, округления Икс разными методами. Для наглядности графики показаны смещенными от целого числа. у ценности. Вфайл SVG, наведите указатель мыши на метод, чтобы выделить его, а в SMIL -включенные браузеры, щелкните, чтобы выбрать или отменить выбор.

Округление означает замену количество с приблизительный ценность, имеющая короче, проще, или более явное представление. Например, замена 23,4476 доллара на 23,45 доллара, дробь 312/937 на 1/3 или выражение √2 с 1.414.

Округление часто выполняется для получения значения, которое легче отчет и общаться чем оригинал. Также важно избегать округления обманчиво точный отчет о вычисленном числе, измерение или оценить; например, количество, которое было вычислено как 123 456, но известно как точный только с точностью до нескольких сотен единиц обычно лучше указать как «около 123 500».

С другой стороны, округление точных чисел приведет к некоторым ошибка округления в сообщенном результате. Округление почти неизбежно при отчетах о большом количестве вычислений, особенно при делении двух чисел на целое число или арифметика с фиксированной точкой; при вычислении математических функций, таких как квадратные корни, логарифмы, и синусы; или при использовании плавающая точка представление с фиксированным количеством значащие цифры. В последовательности вычислений эти ошибки округления обычно накапливать, а в некоторых плохо воспитанный случаях они могут сделать результат бессмысленным.

Точное округление трансцендентные математические функции сложно, потому что количество дополнительных цифр, которые необходимо вычислить, чтобы решить, следует ли округлять в большую или меньшую сторону, невозможно заранее узнать. Эта проблема известна как "дилемма изготовителя стола ".

Округление во многом похоже на квантование это происходит, когда физические величины должны быть закодированы числами или цифровые сигналы.

А волнистый знак равенства (≈: примерно равно) иногда используется для обозначения округления точных чисел, например, 9.98 ≈ 10. Этот знак был введен Альфред Джордж Гринхилл в 1892 г.^[1]

Идеальные характеристики методов округления включают:

Округление должно выполняться функция. Таким образом, когда один и тот же ввод округляется в разных случаях, вывод не изменяется.
Расчеты, выполненные с округлением, должны быть близки к расчетам без округления.
- В результате (1) и (2) результат округления должен быть близок к его входу, часто как можно ближе к некоторым метрика.
Чтобы считать округлением, ассортимент будет подмножеством домен. Классический диапазон - это целые числа, Z.
Округление следует сохранить симметрии которые уже существуют между доменом и диапазоном. С конечной точностью (или дискретный домен), это означает удаление предвзятость.
Метод округления должен быть полезен в информатике или человеческой арифметике, где используется конечная точность и скорость является важным фактором.

Но поскольку метод обычно не может удовлетворить все идеальные характеристики, существует множество методов.

Как правило, округление идемпотент;^[2] т.е. после округления числа повторное округление не изменит его значения. Функции округления также монотонный; т.е. округление большего числа приводит к тому же или большему результату, чем округление меньшего числа.

Виды округления

Типичные проблемы округления включают:

Проблема округления	Пример ввода	Результат	Критерий округления
Приближение иррационального числа дробью	$π$	22 / 7	1-значный знаменатель
Приближая рациональное число на другую дробь с меньшими числителем и знаменателем	399 / 941	3 / 7	1-значный знаменатель
Приближение дроби, имеющей периодическое десятичное разложение, конечной десятичной дробью	5 / 3	1.6667	4 десятичные знаки
Приближая дробное десятичное число на единицу с меньшим количеством цифр	2.1784	2.18	2 знака после запятой
Приближение десятичной дроби целое число на целое число с большим количеством нулей в конце	23,217	23,200	3 значащих цифры
Аппроксимация большой десятичной дроби целое число с помощью научная нотация	300,999,999	3.01 × 10⁸	3 значащих цифры
Приближение значения к указанной сумме, кратной указанной	48.2	45	Кратно 15
Округление каждого из конечного набора действительных чисел (в основном дробей) до целого числа (иногда до второго ближайшего целого числа), чтобы сумма округленных чисел равнялась округленной сумме чисел (требуется, например, [1] для распределение мест, реализовано, например посредством метод наибольшего остатка, увидеть Математика раскладки, и [2] для распределения суммы НДС накладной к ее позициям)	{3/12, 4/12, 5/12}	{0, 0, 1}	Сумма округленных элементов равна округленной сумме элементов

Округление до целого числа

Самая простая форма округления - замена произвольного числа целым. Все следующие режимы округления являются конкретными реализациями абстрактной процедуры round () с одним аргументом. Это настоящие функции (за исключением тех, которые используют случайность).

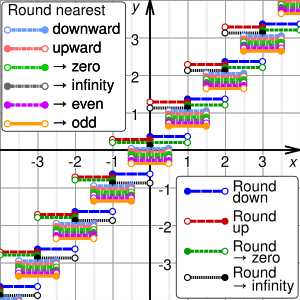
Направленное округление до целого числа

Эти четыре метода называются направленное округление, как смещения от исходного числа Икс к округленному значению у все направлены к одному и тому же предельному значению (0, +∞, или −∞). Направленное округление используется в интервальная арифметика и часто требуется в финансовых расчетах.

Если Икс является положительным, округление в меньшую сторону - это то же самое, что и округление до нуля, а округление в большую сторону - такое же, как округление от нуля. Если Икс является отрицательным, округление в меньшую сторону аналогично округлению от нуля, а округление вверх - как округление до нуля. В любом случае, если Икс целое число, у просто Икс.

Если многие вычисления выполняются последовательно, выбор метода округления может очень сильно повлиять на результат. Известный случай связан с новым показатель создан Фондовая биржа Ванкувера в 1982 году. Первоначально он был установлен на уровне 1 000 000 (с точностью до трех знаков после запятой), а через 22 месяца упал примерно до 520 - тогда как цены на акции в целом увеличилось за этот период. Проблема была вызвана тем, что индекс пересчитывался тысячи раз в день и всегда округлялся до трех знаков после запятой, так что ошибки округления накапливались. Пересчет с лучшим округлением дал значение индекса 1098,892 на конец того же периода.^[3]

В приведенных ниже примерах $sgn (Икс)$ относится к функция знака применяется к исходному номеру, $Икс$ .

Округление в меньшую сторону

округлить вниз (или возьмите этаж, или округлить до минус бесконечности): у - наибольшее целое число, не превышающее Икс.
${ displaystyle y = mathrm {floor} (x) = left lfloor x right rfloor = - left lceil -x right rceil}$

Например, 23,7 округляется до 23, а -23,2 округляется до -24.

Округления

округлять (или возьмите потолок, или округлить в сторону плюс бесконечности): у это наименьшее целое число, которое не меньше, чем Икс.
${ displaystyle y = operatorname {ceil} (x) = left lceil x right rceil = - left lfloor -x right rfloor}$

Например, 23,2 округляется до 24, а -23,7 округляется до -23.

Округление в сторону нуля

округлить до нуля (или обрезать, или округлить от бесконечности): у это целое число, наиболее близкое к Икс такой, что он находится между 0 и Икс (в комплекте); т.е. у это целая часть Икс, без цифр дробной части.
${ displaystyle y = operatorname {truncate} (x) = operatorname {sgn} (x) left lfloor left | x right | right rfloor = - operatorname {sgn} (x) left lceil - left | x right | right rceil}$

Например, 23,7 округляется до 23, а -23,7 округляется до -23.

Округление от нуля

округлить от нуля (или к бесконечности): у - целое число, которое ближе всего к 0 (или, что то же самое, к Икс) такие, что Икс находится между 0 и у (в комплекте).
${ displaystyle y = operatorname {sgn} (x) left lceil left | x right | right rceil = - operatorname {sgn} (x) left lfloor - left | x right | right rfloor}$

Например, 23,2 округляется до 24, а -23,2 округляется до -24.

Округление до ближайшего целого числа

Округление числа Икс к ближайшему целому числу требует некоторого правила разрыва связи для тех случаев, когда Икс находится ровно посередине между двумя целыми числами, то есть когда дробная часть Икс ровно 0,5.

Если бы не дробные части 0,5, ошибки округления, вносимые методом округления до ближайшего, были бы симметричными: для каждой дробной части, которая округляется в меньшую сторону (например, 0,268), существует дополнительная дробь (а именно 0,732), которая округляется на ту же сумму.

При округлении большого набора фиксированная точка числа с равномерно распределены дробные части, ошибки округления по всем значениям, за исключением тех, которые имеют 0,5 дробной части, будут статистически компенсировать друг друга. Это означает, что ожидаемое (среднее) значение округленных чисел равно ожидаемому значению исходных чисел, когда мы удаляем из набора числа с дробной частью 0,5.

На практике, плавающая точка обычно используются числа, которые имеют еще больше вычислительных нюансов, потому что они неравномерно расположены.

Округлить до половины

Следующее правило разрешения ничьей, называемое округлить до половины (или округлить половину в сторону положительной бесконечности), широко используется во многих дисциплинах.^{[нужна цитата ]} То есть половинные значения Икс всегда округляются.

Если доля Икс равно 0,5, то у = Икс + 0.5
${ displaystyle y = left lfloor x + 0,5 right rfloor = - left lceil -x-0,5 right rceil = left lceil { frac { lfloor 2x rfloor} {2}} право rceil}$

Например, 23,5 округляется до 24, а -23,5 округляется до -23.

Однако некоторые языки программирования (например, Java, Python) определяют свои половина вверх так как округлить до половины от нуля Вот.^[4]^[5]

Этот метод требует проверки только одной цифры, чтобы определить направление округления в два дополнения и подобные представления.

Округлить наполовину вниз

Также можно использовать округлить до половины (или округлить половину в сторону отрицательной бесконечности) в отличие от более распространенных округлить до половины.

Если доля Икс равно 0,5, то у = Икс − 0.5
${ displaystyle y = left lceil x-0,5 right rceil = - left lfloor -x + 0,5 right rfloor = left lfloor { frac { lceil 2x rceil} {2}} правый rfloor}$

Например, 23,5 округляется до 23, а -23,5 округляется до -24.

Округлить половину к нулю

Можно также округлить половину к нулю (или круглая половина от бесконечности) в отличие от обычного округлить до половины от нуля.

Если доля Икс равно 0,5, то у = Икс - 0,5, если Икс положительный, и у = Икс + 0,5, если Икс отрицательный.
${ displaystyle y = operatorname {sgn} (x) left lceil left | x right | -0,5 right rceil = - operatorname {sgn} (x) left lfloor - left | x right | +0,5 right rfloor}$

Например, 23,5 округляется до 23, а -23,5 округляется до -23.

Этот метод обрабатывает положительные и отрицательные значения симметрично и, следовательно, свободен от общего положительного / отрицательного смещения, если исходные числа являются положительными или отрицательными с равной вероятностью. Однако он все еще имеет тенденцию к нулю.

Округлить половину от нуля

Еще один метод, который обычно преподают и используют, - это округлить до половины от нуля (или округлить половину к бесконечности), а именно:

Если доля Икс равно 0,5, то у = Икс + 0,5, если Икс положительный, и у = Икс - 0,5, если Икс отрицательный.
${ displaystyle y = operatorname {sgn} (x) left lfloor left | x right | +0,5 right rfloor = - operatorname {sgn} (x) left lceil - left | x right | -0,5 right rceil}$

Например, 23,5 округляется до 24, а -23,5 округляется до -24.

Это может быть более эффективным на двоичных компьютерах, потому что нужно учитывать только первый пропущенный бит, чтобы определить, округляется ли он в большую (1) или в меньшую (0) сторону. Это один из методов округления до значимые фигуры благодаря своей простоте.

Этот метод, также известный как коммерческое округление, обрабатывает положительные и отрицательные значения симметрично и, следовательно, не имеет общего положительного / отрицательного смещения, если исходные числа являются положительными или отрицательными с равной вероятностью. Однако он все еще имеет смещение от нуля.^{[нужна цитата ]}.

Он часто используется для конвертации валют и округления цен (когда сумма сначала конвертируется в наименьшую значительную часть валюты, например центы евро), поскольку это легко объяснить, просто рассматривая первую дробную цифру, независимо от дополнительных точные цифры или знак суммы (для строгого равенства между плательщиком и получателем суммы).

Округлить половину до четного

Правило разрешения ничьей без положительной / отрицательной предвзятости и без смещения в сторону / от нуля округлить до половины. По этому соглашению, если дробная часть Икс равно 0,5, то у является ближайшим к Икс. Так, например, +23,5 становится +24, как и +24,5; в то время как -23,5 становится -24, как и -24,5. Эта функция сводит к минимуму ожидаемую ошибку при суммировании округленных цифр, даже если входные данные в основном положительные или в основном отрицательные.

Этот вариант метода округления до ближайшего еще называется сходящееся округление, округление статистики, Голландское округление, Гауссово округление, нечетно-четное округление,^[6] или банкиров округление.

Это режим округления по умолчанию, используемый в IEEE 754 операции для результатов в двоичных форматах с плавающей запятой (см. также ближайшая целочисленная функция ), и более сложный режим^{[требуется разъяснение ]} используется при округлении до значащих цифр.

За счет устранения систематической ошибки повторное округленное сложение или вычитание независимых чисел даст результат с ошибкой, которая имеет тенденцию расти пропорционально квадратному корню из числа операций, а не линейно. Увидеть случайная прогулка для большего.

Однако это правило искажает распределение, увеличивая вероятность равных по сравнению с шансами. Обычно это менее важно, чем смещения, которые устраняются этим методом.^{[нужна цитата ]}.

Округлить половину до нечетного

Похожее правило разрешения ничьей округлить половину до нечетного. В этом подходе, если доля Икс равно 0,5, то у нечетное целое число, ближайшее к Икс. Так, например, +23,5 становится +23, как и +22,5; в то время как -23,5 становится -23, как и -22,5.

Этот метод также свободен от положительного / отрицательного смещения и смещения в сторону / от нуля.

Этот вариант почти никогда не используется в вычислениях, за исключением ситуаций, когда нужно избежать увеличения масштаба чисел с плавающей запятой, которые имеют ограниченный диапазон экспоненты. С участием округлить до половины, небесконечное число будет округлено до бесконечности, а небольшое ненормальный значение будет округлено до нормального ненулевого значения. Фактически, этот режим предпочитает сохранять существующую шкалу связанных чисел, избегая результатов, выходящих за пределы диапазона, когда это возможно для систем счисления четных чисел. основание (например, двоичное и десятичное).^{[требуется разъяснение (увидеть говорить)]}

Рандомизированное округление до целого числа

Чередование тай-брейков

Один из способов, более непонятный, чем большинство других, - это изменение направления при округлении числа до 0,5 дробной части. Все остальные округляются до ближайшего целого числа.

Если дробная часть равна 0,5, попеременное округление в большую или меньшую сторону: при первом появлении дробной части 0,5 округление в большую сторону; для второго случая округлить в меньшую сторону; и так далее. (В качестве альтернативы округление первой дробной части 0,5 может быть определено случайное семя.)

Если вхождений 0,5 дробных частей происходит значительно чаще, чем перезапуск «подсчета» вхождений, то это эффективно без смещения. С гарантированным нулевым смещением это полезно, если числа должны быть суммированы или усреднены.

Случайный тай-брейк

Если дробная часть Икс равно 0,5, выберите у случайно среди Икс + 0.5 и Икс − 0.5, с равной вероятностью. Все остальные округляются до ближайшего целого числа.

Подобно округлению половин к четным и половинным к нечетным, это правило по существу свободно от общей систематической ошибки, но оно также справедливо для четных и нечетных у ценности. Преимущество перед альтернативным разделением связей состоит в том, что последнее направление округления дробной части 0,5 не нужно «запоминать».

Стохастическое округление

Округление до одного из ближайших целых чисел с вероятностью, зависящей от близости, называется стохастический округление и в среднем даст объективный результат.^[7]

{ displaystyle operatorname {Round} (x) = { begin {cases} lfloor x rfloor & { text {с вероятностью}} 1- (x- lfloor x rfloor) lfloor x rfloor +1 & { text {с вероятностью}} {x- lfloor x rfloor} end {cases}}}

Например, 1,6 будет округлено до 1 с вероятностью 0,4 и до 2 с вероятностью 0,6.

Стохастическое округление точно так же, как округление функция никогда не может быть. Например, предположим, что вы начали с 0 и добавили к нему 0,3 сто раз, округляя промежуточную сумму между каждым добавлением. Результатом будет 0 при обычном округлении, но при стохастическом округлении ожидаемый результат будет 30, что является таким же значением, полученным без округления. Это может быть полезно в машинное обучение где при обучении может использоваться итеративная арифметика с низкой точностью.^[7] Стохастическое округление - это способ достижения одномерного дизеринга.

Сравнение подходов к округлению до целого числа

Ценность	Функциональные методы										Рандомизированные методы
	Направленное округление				Округлить до ближайшего						Чередование тай-брейков		Случайный тай-брейк		Стохастик
	вниз (в сторону -∞)	Вверх (в сторону +∞)	К 0	Далеко от 0	Половина вниз (в сторону -∞)	Half Up (в сторону +∞)	Половина к 0	На полпути от 0	От половины до даже	От половины до нечетного	Средний	SD	Средний	SD	Средний	SD
+1.8	+1	+2	+1	+2	+2	+2	+2	+2	+2	+2	+2	0	+2	0	+1.8	0.04
+1.5					+1	+2	+1	+2	+2	+1	+1.505	0	+1.5	0.05	+1.5	0.05
+1.2						+1		+1	+1		+1	0	+1	0	+1.2	0.04
+0.8	0	+1	0	+1					+1		+1	0	+1	0	+0.8	0.04
+0.5					0		0		0		+0.505	0	+0.5	0.05	+0.5	0.05
+0.2						0		0		0	0	0	0	0	+0.2	0.04
−0.2	−1	0		−1				0		0	0	0	0	0	−0.2	0.04
−0.5					−1			−1		−1	−0.495	0	−0.5	0.05	−0.5	0.05
−0.8						−1	−1		−1		−1	0	−1	0	−0.8	0.04
−1.2	−2	−1	−1	−2					−1		−1	0	−1	0	−1.2	0.04
−1.5					−2			−2	−2		−1.495	0	−1.5	0.05	−1.5	0.05
−1.8					−2	−2	−2	−2	−2	−2	−2	0	−2	0	−1.8	0.04

Округление до других значений

Округление до указанного кратного

Наиболее распространенный тип округления - округление до целого числа; или, в более общем смысле, до целого числа, кратного некоторому приращению - например, округление до целых десятых долей секунды, сотых долей доллара, до целых кратных 1/2 или 1/8 дюйма, до целых десятков или тысяч и т. д.

В общем, округление числа Икс до кратного некоторого указанного положительного значения м влечет за собой следующие шаги:

{ Displaystyle mathrm {roundToMultiple} (x, m) = mathrm {round} (x / m) times m}

Например, округление Икс = 2,1784 доллара в центах (то есть до кратного 0,01) влечет за собой вычисление 2,1784 / 0,01 = 217,84, затем округление до 218 и, наконец, вычисление 218 × 0,01 = 2,18.

При округлении до заданного количества значащие цифры, приращение м зависит от величины округляемого числа (или от округляемого результата).

Приращение м обычно является конечной дробью в любом система счисления используется для представления чисел. Для показа людям это обычно означает десятичная система счисления (это, м целое число, умноженное на мощность из 10, например 1/1000 или 25/100). Для промежуточных значений, хранящихся в цифровых компьютерах, это часто означает двоичная система счисления (м является целым числом, умноженным на степень 2).

Абстрактная функция с одним аргументом round (), которая возвращает целое число из произвольного реального значения, имеет как минимум дюжину различных конкретных определений, представленных в округление до целого числа раздел. Абстрактная функция с двумя аргументами roundToMultiple () формально определена здесь, но во многих случаях она используется с неявным значением м = 1 для приращения, а затем сводится к эквивалентной абстрактной функции с одним аргументом, также с той же дюжиной различных конкретных определений.

Логарифмическое округление

Округление до указанной степени

Округление до указанного мощность сильно отличается от округления до указанного множественный; например, в вычислительной технике часто требуется округлять число до целой степени 2. Как правило, шаги для округления положительного числа Икс в степени некоторого указанного целого числа б больше 1, являются:

{ displaystyle mathrm {roundToPower} (x, b) = b ^ { mathrm {round} ( log _ {b} x)}}

Многие предостережения, применимые к округлению до кратного, применимы и к округлению до степени.

Масштабированное округление

Этот вид округления, который еще называют округление до логарифмической шкалы, это вариант округление до указанной степени. Округление по логарифмической шкале осуществляется путем принятия логарифма суммы и выполнения обычного округления до ближайшего значения в логарифмической шкале.

Например, резисторы поставляются с предпочтительные числа в логарифмической шкале. В частности, для резисторов с точностью до 10% они поставляются с номиналами 100, 120, 150, 180, 220 и т.д., округленными до кратных 10 (E12 серия ). Если расчет показывает, что требуется резистор на 165 Ом, то log (150) = 2,176, log (165) = 2,217 и log (180) = 2,255. Логарифм 165 ближе к логарифму 180, поэтому резистор на 180 Ом был бы первым выбором, если нет других соображений.

Будь то значение $Икс \in (а, б)$ раундов к а или б зависит от того, $Икс 2$ больше или меньше продукта $ab$ . Значение 165 округляется до 180 в примере резисторов, потому что $1652 = 27225$ больше, чем $150 \times 180 = 27000$ .

Округление с плавающей запятой

В арифметика с плавающей запятой, округление направлено на то, чтобы превратить заданное значение Икс в ценность у с указанным количеством существенный цифры. Другими словами, у должно быть кратным числу м это зависит от величины Икс. Число м это сила база (обычно 2 или 10) представления с плавающей запятой.

Помимо этой детали, все варианты округления, рассмотренные выше, применимы и к округлению чисел с плавающей запятой. Алгоритм такого округления представлен в Масштабированное округление раздел выше, но с постоянным коэффициентом масштабирования s = 1 и целое основание б > 1.

Если округленный результат будет переполнять результат для направленного округления, это либо соответствующая бесконечность со знаком при «округлении от нуля», либо наивысшее представимое положительное конечное число (или наименьшее представимое отрицательное конечное число, если Икс отрицательно) при «округлении в сторону нуля». Результат переполнения для обычного случая округлить до ближайшего всегда подходящая бесконечность.

Округление до простой дроби

В некоторых случаях желательно округлить данное число Икс в «чистую» дробь - то есть ближайшую дробь у = м/п чей числитель м и знаменатель п не превышайте заданный максимум. Эта проблема довольно сильно отличается от проблемы округления значения до фиксированного числа десятичных или двоичных цифр или до числа, кратного данной единице. м. Эта проблема связана с Последовательности Фари, то Стерн – Броко, и непрерывные дроби.

Округление до доступного значения

Законченный пиломатериалы, писчая бумага, конденсаторы и многие другие товары обычно продаются только в нескольких стандартных размерах.

Многие процедуры проектирования описывают, как вычислить приблизительное значение, а затем «округлить» до некоторого стандартного размера с помощью таких фраз, как «округлить до ближайшего стандартного значения», «округлить до ближайшего стандартного значения» или «округлить до ближайшего стандартного значения». .^[8]^[9]

Когда набор предпочтительные значения равномерно распределены по логарифмической шкале, выбирая ближайший предпочтительное значение к любому заданному значению можно рассматривать как форму масштабное округление. Такие округленные значения можно вычислить напрямую.^[10]

Округление в других контекстах

Дизеринг и распространение ошибок

При оцифровке непрерывные сигналы Например, звуковые волны, общий эффект от ряда измерений более важен, чем точность каждого отдельного измерения. В этих обстоятельствах дизеринг, и связанная техника, распространение ошибок, обычно используются. Связанный метод называется широтно-импульсная модуляция используется для получения выходного сигнала аналогового типа от инерциального устройства путем быстрой подачи импульсов мощности с переменной скважностью.

Распространение ошибок пытается гарантировать, что ошибка в среднем сведена к минимуму.При пологом наклоне от единицы до нуля выход будет равен нулю для первых нескольких членов, пока сумма ошибки и текущего значения не станет больше 0,5, и в этом случае выводится 1, а разница вычитается из ошибки. так далеко. Дизеринг Флойда – Стейнберга это популярная процедура распространения ошибок при оцифровке изображений.

В качестве одномерного примера предположим, что числа $0.9677$ , $0.9204$ , $0.7451$ , и $0.3091$ происходят по порядку, и каждое значение округляется до кратного $0.01$ . В этом случае совокупные суммы, $0.9677$ , $1.8881 = 0.9677 + 0.9204$ , $2.6332 = 0.9677 + 0.9204 + 0.7451$ , и $2.9423 = 0.9677 + 0.9204 + 0.7451 + 0.3091$ , округляются до кратного $0.01$ : $0.97$ , $1.89$ , $2.63$ , и $2.94$ . Первое из них и различия соседних значений дают желаемые округленные значения: $0.97$ , $0.92 = 1.89 - 0.97$ , $0.74 = 2.63 - 1.89$ , и $0.31 = 2.94 - 2.63$ .

Арифметика Монте-Карло

Арифметика Монте-Карло - это метод в Методы Монте-Карло где округление происходит случайным образом в большую или меньшую сторону. Стохастическое округление может использоваться для арифметики Монте-Карло, но в целом чаще используется просто округление в большую или меньшую сторону с равной вероятностью. Повторные прогоны дадут случайное распределение результатов, которое может указывать на стабильность вычислений.^[11]

Точное вычисление с округленной арифметикой

Можно использовать округленную арифметику для оценки точного значения функции с целочисленным доменом и диапазоном. Например, если мы знаем, что целое число п идеальный квадрат, мы можем вычислить его квадратный корень, преобразовав п к значению с плавающей запятой z, вычисляя приближенный квадратный корень Икс из z с плавающей точкой, а затем округление Икс к ближайшему целому числу у. Если п не слишком большой, ошибка округления с плавающей запятой в Икс будет меньше 0,5, поэтому округленное значение у будет точным квадратным корнем из п. По сути, поэтому правила слайдов может использоваться для точной арифметики.

Двойное округление

Округление числа дважды подряд до различных уровней точности, причем последняя точность является более грубой, не гарантирует того же результата, что и однократное округление до конечной точности, за исключением случая направленного округления.^{[nb 1]} Например, округление 9,46 до одного десятичного знака дает 9,5, а затем 10 при округлении до целого числа с использованием округления половины до четного, но даст 9 при непосредственном округлении до целого числа. Борман и Чатфилд^[12] обсудить последствия двойного округления при сравнении данных, округленных до одного десятичного знака, с пределами спецификации, выраженными с помощью целых чисел.

В Мартинес против Allstate и Сендехо против фермеровВ судебном процессе между 1995 и 1997 годами страховые компании утверждали, что двойное округление премий допустимо и фактически необходимо. Суды США вынесли решение против страховых компаний и предписали им принять правила, обеспечивающие однократное округление.^[13]

Некоторые компьютерные языки и IEEE 754-2008 Согласно стандарту, при простых вычислениях результат не следует округлять дважды. Это было особой проблемой для Java, поскольку она разработана для идентичной работы на разных машинах, и для этого пришлось использовать специальные приемы программирования. x87 плавающая точка.^[14]^[15]Язык Java был изменен, чтобы разрешить разные результаты, где разница не имеет значения и требует strictfp квалификатор, который будет использоваться, когда результаты должны точно соответствовать.

В некоторых алгоритмах промежуточный результат вычисляется с большей точностью, а затем должен быть округлен до конечной точности. Двойного округления можно избежать, выбрав соответствующее округление для промежуточных вычислений. Это состоит в том, чтобы избегать округления до средних точек для окончательного округления (кроме случаев, когда средняя точка точна). В двоичной арифметике идея состоит в том, чтобы округлить результат до нуля и установить младший бит в 1, если округленный результат неточен; это округление называется липкое округление.^[16] Эквивалентно, он состоит в возврате промежуточного результата, когда он точно представим, и ближайшего числа с плавающей запятой с нечетным значением в противном случае; вот почему он также известен как округление до нечетного.^[17]^[18]

Дилемма изготовителя стола

Уильям М. Кахан придумал термин «дилемма производителя стола» для неизвестной стоимости округления трансцендентные функции:

"Никто не знает, сколько будет стоить вычисление у^ш правильно округлено для каждый два аргумента с плавающей запятой, при которых он не переполняется / не уменьшается. Вместо этого авторитетные математические библиотеки вычисляют элементарно трансцендентные функции в основном в пределах чуть более половины трепыхаться и почти всегда в пределах одной миски. Почему не может у^ш округляться до половины мультика, как SQRT? Потому что никто не знает, сколько это будет стоить вычислений ... Не существует общего способа предсказать, сколько дополнительных цифр потребуется перенести, чтобы вычислить трансцендентное выражение и округлить его. правильно до некоторого заранее заданного количества цифр. Даже тот факт (если это правда), что в конечном итоге будет достаточно конечного числа дополнительных цифр, может быть глубокой теоремой ".^[19]

В IEEE 754 Стандарт с плавающей запятой гарантирует, что сложение, вычитание, умножение, деление, слитное умножение – сложение, квадратный корень и остаток с плавающей запятой дадут правильно округленный результат операции бесконечной точности. В стандарте 1985 года такой гарантии не было для более сложных функций, и они, как правило, в лучшем случае имеют точность только до последнего бита. Однако стандарт 2008 гарантирует, что соответствующие реализации дадут правильно округленные результаты с учетом активного режима округления; однако реализация функций не является обязательной.

С использованием Теорема Гельфонда – Шнайдера и Теорема Линдемана – Вейерштрасса можно доказать, что многие стандартные элементарные функции возвращают трансцендентный результаты, когда даны рациональные ненулевые аргументы; поэтому всегда можно правильно округлить такие функции. Однако определение предела для данной точности того, насколько точные результаты должны быть вычислены, прежде чем можно будет гарантировать правильно округленный результат, может потребовать много времени вычислений или может оказаться недосягаемым.^[20] На практике, когда этот предел неизвестен или слишком велик, в реализации должно быть принято какое-то решение (см. Ниже), но согласно вероятностной модели правильное округление может выполняться с очень высокой вероятностью.

Некоторые программные пакеты предлагают правильное округление. В GNU MPFR пакет дает правильно округленные результаты произвольной точности. Некоторые другие библиотеки реализуют элементарные функции с правильным округлением с двойной точностью:

IBM libultim, только с округлением до ближайшего.^[21] Эта библиотека использует до 768 бит рабочей точности.
Sun Microsystems libmcr в 4 режимах округления.^[22] Для сложных случаев эта библиотека также использует множественную точность, и количество слов увеличивается на 2 каждый раз, когда возникает дилемма создателя таблиц (с неопределенным поведением в очень маловероятном случае, когда достигается некоторый предел машины).
CRlibm, написанный в старой команде Arénaire (LIP, ENS Lyon ). Он поддерживает 4 режима округления и зарекомендовал себя.^[23]

Существуют вычислимые числа для которых невозможно определить округленное значение, независимо от того, сколько цифр вычислено. Конкретных примеров привести нельзя, но это следует из неразрешимости проблема остановки. Например, если Гипотеза Гольдбаха правда, но недоказуемо, то результат округления следующего значения до следующего целого не может быть определен: 1 + 10^−п где п - первое четное число больше 4, которое не является суммой двух простых чисел, или 1, если такого числа нет. Округленный результат равен 2, если такое число п существует и 1 в противном случае. Однако значение до округления может быть приближено с любой заданной точностью, даже если предположение недоказуемо.

Взаимодействие со строковым поиском

Округление может отрицательно сказаться на строковом поиске числа. Например, $π$ с округлением до четырех цифр - "3,1416", но простой поиск этой строки не обнаружит "3,14159" или любое другое значение $π$ округляется до более чем четырех цифр. Напротив, усечение не страдает этой проблемой; например, простой строковый поиск «3,1415», который $π$ усеченный до четырех цифр, обнаружит значения $π$ усечено до более чем четырех цифр.

История

Концепция округления очень старая, возможно, даже старше, чем концепция деления. Некоторые древние глиняные таблички нашел в Месопотамия содержат таблицы с округленными значениями взаимные и квадратные корни по основанию 60.^[24]Округленные приближения к $π$ , длина года и длина месяца также древние - см. база 60 примеров.

В округлый метод послужил ASTM (E-29) стандарт с 1940 года. Происхождение терминов беспристрастное округление и округление статистики довольно понятны. В четвертом издании 1906 г. Вероятность и теория ошибок^[25] Роберт Симпсон Вудворд назвал это "правилом компьютера", указывая на то, что в то время оно широко использовалось человеческие компьютеры кто рассчитывал математические таблицы. Черчилль Эйзенхарт указали, что к 1940-м годам эта практика уже была «прочно закрепилась» в анализе данных.^[26]

Происхождение термина банкиров округление остается более неясным. Если этот метод округления когда-либо был стандартом в банковской сфере, доказательства оказалось чрезвычайно трудно найти. Напротив, раздел 2 отчета Европейской комиссии Введение евро и округление валютных сумм^[27] предполагает, что ранее не существовало стандартного подхода к округлению в банковской сфере; и в нем указано, что «промежуточные» суммы должны округляться в большую сторону.

До 1980-х годов метод округления, используемый в компьютерной арифметике с плавающей запятой, обычно фиксировался аппаратным обеспечением, плохо документировался, несовместим и отличался для каждой марки и модели компьютера. Эта ситуация изменилась после того, как стандарт IEEE 754 с плавающей запятой был принят большинством производителей компьютеров. Стандарт позволяет пользователю выбирать один из нескольких режимов округления и в каждом случае точно определяет, как следует округлять результаты. Эти особенности сделали численные вычисления более предсказуемыми и машинно-независимыми, а также сделали возможной эффективную и последовательную реализацию интервальная арифметика.

В настоящее время многие исследования округляются до значений, кратных 5 или 2. Например, Йорг Батен используемый возрастная куча во многих исследованиях для оценки уровня навыков счета древнего населения. Он придумал Индекс ABCC, что позволяет сравнивать умение считать среди регионов возможно без каких-либо исторических источников, где население грамотность был измерен.^[28]

Функции округления в языках программирования

Наиболее языки программирования предоставлять функции или специальный синтаксис для округления дробных чисел различными способами. Самые ранние числовые языки, такие как FORTRAN и C, предоставит только один метод, обычно усечение (в сторону нуля). Этот метод по умолчанию может подразумеваться в определенных контекстах, например, при присвоении дробного числа элементу целое число переменная, или используя дробное число в качестве индекса массив. Остальные виды округления нужно было запрограммировать явно; например, округление положительного числа до ближайшего целого числа может быть реализовано путем добавления 0,5 и усечения.

Однако в последние десятилетия синтаксис и / или стандарт библиотеки Большинство языков обычно предоставляют по крайней мере четыре основные функции округления (вверх, вниз, до ближайшего и к нулю). Метод разрешения конфликтов может варьироваться в зависимости от языка и версии и / или может выбираться программистом. Несколько языков следуют примеру стандарта IEEE 754 с плавающей запятой и определяют эти функции как поплавок двойной точности аргумент и возвращает результат того же типа, который затем при необходимости может быть преобразован в целое число. Такой подход может избежать ложных переливается потому что типы с плавающей запятой имеют больший диапазон, чем целочисленные типы. Некоторые языки, например PHP, предоставить функции, округляющие значение до указанного числа десятичных цифр, например от 4321,5678 до 4321,57 или 4300. Кроме того, многие языки предоставляют printf или аналогичная функция форматирования строки, которая позволяет преобразовать дробное число в строку, округленную до указанного пользователем количества десятичных знаков ( точность). С другой стороны, усечение (округление до нуля) по-прежнему является методом округления по умолчанию, используемым во многих языках, особенно для деления двух целых значений.

Напротив, CSS и SVG не определяют какой-либо конкретной максимальной точности для чисел и измерений, которые рассматриваются и выставляются в их ДОМ и в их IDL интерфейс как строки, как если бы они бесконечная точность, и не делают различий между целыми числами и значениями с плавающей запятой; однако реализации этих языков обычно преобразуют эти числа в значения с плавающей запятой двойной точности IEEE 754, прежде чем отображать вычисленные цифры с ограниченной точностью (особенно в пределах стандартной JavaScript или ECMAScript^[29] привязки интерфейса).

Другие стандарты округления

Некоторые дисциплины или учреждения выпустили стандарты или директивы для округления.

Наблюдения за погодой в США

В руководстве, выпущенном в середине 1966 г.,^[30] то НАС. Управление Федерального координатора по метеорологии определило, что метеорологические данные следует округлять до ближайшего округленного числа с использованием правила разрыва связей «округлять половину вверх». Например, 1,5, округленное до целого числа, должно стать 2, а -1,5 должно стать -1. До этой даты правилом разделения ставок было «округление до половины от нуля».

Отрицательный ноль в метеорологии

Немного метеорологи может написать «-0», чтобы указать температуру от 0,0 до -0,5 градусов (исключая), которая была округлена до целого числа. Это обозначение используется, когда отрицательный знак считается важным, независимо от того, насколько мала величина; например, при округлении температур в Цельсия шкала, где минус 0 означает замерзание.^{[нужна цитата ]}

Смотрите также

Точные таблицы Гала
Интервальная арифметика
ISO 80000-1
Алгоритм суммирования Кахана
Ближайшая целочисленная функция
Усечение
Знаковое представление
Пропорциональное представительство по партийным спискам - это приложение для округления целых чисел, которое было тщательно исследовано
Округление наличных денег, имея дело с отсутствием очень дешевых монет

Примечания

^ Другой случай, когда двойное округление всегда приводит к тому же значению, что и прямое округление до конечной точности, - это когда система счисления является нечетной.

использованная литература

^ Исайя Лэнкхэм, Бруно Нахтергаэле, Энн Шиллинг: Линейная алгебра как введение в абстрактную математику. World Scientific, Сингапур, 2016 г., ISBN 978-981-4730-35-8, п. 186.
^ Кулиш, Ульрих В. (Июль 1977 г.). «Математические основы компьютерной арифметики». Транзакции IEEE на компьютерах. С-26 (7): 610–621. Дои:10.1109 / TC.1977.1674893.
^ Хайэм, Николас Джон (2002). Точность и стабильность численных алгоритмов. п.54. ISBN 978-0-89871-521-7.
^ "java.math.RoundingMode". Oracle.
^ "decimal - десятичная арифметика с фиксированной и плавающей запятой". Фонд программного обеспечения Python.
^ Руководство по разработке технических стандартов (НАСА), X-673-64-1F, стр90
^ ^а ^б Гупта, Суйог; Angrawl, Анкур; Гопалакришнан, Кайлас; Нараянан, Притиш (09.02.2016). «Глубокое обучение с ограниченной числовой точностью». п. 3. arXiv:1502.02551 [cs.LG ].
^ "Стабилитроны стабилизаторы напряжения"
^ "Создайте тестер зеркала"
^ Брюс Трамп, Кристин Шнайдер. «Формула Excel вычисляет стандартные значения сопротивления 1%».Электронный дизайн, 2002-01-21.[1]
^ Паркер, Д. Стотт; Eggert, Paul R .; Пирс, Брэд (28 марта 2000). «Арифметика Монте-Карло: основа для статистического анализа ошибок округления». Вычисления IEEE в науке и технике.
^ Борман, Фил; Чатфилд, Мэрион (10 ноября 2015 г.). «Избегайте опасности использования округленных данных». Журнал фармацевтического и биомедицинского анализа. 115: 506–507. Дои:10.1016 / j.jpba.2015.07.021. PMID 26299526.
^ Дебора Р. Хенслер (2000). Дилеммы коллективного иска: преследование общественных целей ради личной выгоды. РЭНД. стр.255–293. ISBN 0-8330-2601-1.
^ Сэмюэл А. Фигероа (июль 1995 г.). «Когда двойное округление безобидно?». Информационный бюллетень ACM SIGNUM. ACM. 30 (3): 21–25. Дои:10.1145/221332.221334.
^ Роджер Голливер (октябрь 1998 г.). «Эффективное создание ортогональных двойных результатов IEEE по умолчанию с использованием расширенного оборудования IEEE» (PDF). Intel.
^ Мур, Дж. Стротер; Линч, Том; Кауфманн, Мэтт (1996). «Механически проверенное доказательство правильности ядра алгоритма деления с плавающей запятой AMD5K86» (PDF). Транзакции IEEE на компьютерах. 47. CiteSeerX 10.1.1.43.3309. Дои:10.1109/12.713311. Получено 2016-08-02.
^ Болдо, Сильви; Мелькионд, Гийом (2008). «Эмуляция FMA и правильно округленных сумм: проверенные алгоритмы с округлением до нечетных» (PDF). Транзакции IEEE на компьютерах. 57 (4): 462–471. Дои:10.1109 / TC.2007.70819. Получено 2016-08-02.
^ "21718 - real.c округление не идеально". gcc.gnu.org.
^ Кахан, Уильям Мортон. "Слишком умный логарифм". Получено 2008-11-14.
^ Мюллер, Жан-Мишель; Брисебар, Николас; де Динешен, Флоран; Жаннерод, Клод-Пьер; Лефевр, Винсент; Мелькионд, Гийом; Revol, Натали; Stehlé, Damien; Торрес, Серж (2010). «Глава 12: Решение дилеммы производителя стола». Справочник по арифметике с плавающей точкой (1-е изд.). Биркхойзер. Дои:10.1007/978-0-8176-4705-6. ISBN 978-0-8176-4704-9. LCCN 2009939668.
^ "libultim - окончательная библиотека элементарных функций с правильными округлениями".
^ "libmcr - библиотека элементарных функций с правильными округлениями".
^ «CRlibm - математическая библиотека с правильным округлением». Архивировано из оригинал на 2016-10-27.
^ Дункан Дж. Мелвилл. «Глиняная таблетка YBC 7289». 2006 г.
^ «Вероятность и теория ошибок». Historical.library.cornell.edu.
^ Черчилль Эйзенхарт (1947). «Влияние округления или группировки данных». В Эйзенхарте; Хастай; Уоллис (ред.). Избранные методы статистического анализа для научных и промышленных исследований, а также производства и управления. Нью-Йорк: Макгроу-Хилл. стр. 187–223. Получено 2014-01-30.
^ http://ec.europa.eu/economy_finance/publications/publication1224_en.pdf
^ Батен, Йорг (2009). «Количественная оценка грамотности: возрастная куча и история человеческого капитала» (PDF). Журнал экономической истории. 69 (3): 783–808. Дои:10.1017 / S0022050709001120. HDL:10230/481.
^ «Спецификация языка ECMA-262 ECMAScript» (PDF). ecma-international.org.
^ OFCM, 2005 г .: Федеральный метеорологический справочник № 1 В архиве 1999-04-20 на Wayback Machine, Вашингтон, округ Колумбия, 104 с.

внешняя ссылка

Вайсштейн, Эрик В. «Округление». MathWorld.
Введение в различные алгоритмы округления это доступно для широкой аудитории, но особенно полезно для тех, кто изучает информатику и электронику.
Как реализовать пользовательские процедуры округления от Microsoft (сломано)

[NB_Double-12] Другой случай, когда двойное округление всегда приводит к тому же значению, что и прямое округление до конечной точности, - это когда система счисления является нечетной.

[1] Исайя Лэнкхэм, Бруно Нахтергаэле, Энн Шиллинг: Линейная алгебра как введение в абстрактную математику. World Scientific, Сингапур, 2016 г., ISBN 978-981-4730-35-8, п. 186.

[2] Кулиш, Ульрих В. (Июль 1977 г.). «Математические основы компьютерной арифметики». Транзакции IEEE на компьютерах. С-26 (7): 610–621. Дои:10.1109 / TC.1977.1674893.

[3] Хайэм, Николас Джон (2002). Точность и стабильность численных алгоритмов. п.54. ISBN 978-0-89871-521-7.

[4] "java.math.RoundingMode". Oracle.

[5] "decimal - десятичная арифметика с фиксированной и плавающей запятой". Фонд программного обеспечения Python.

[6] Руководство по разработке технических стандартов (НАСА), X-673-64-1F, стр90

[stochastic-7] а ^б Гупта, Суйог; Angrawl, Анкур; Гопалакришнан, Кайлас; Нараянан, Притиш (09.02.2016). «Глубокое обучение с ограниченной числовой точностью». п. 3. arXiv:1502.02551 [cs.LG ].

[8] "Стабилитроны стабилизаторы напряжения"

[9] "Создайте тестер зеркала"

[10] Брюс Трамп, Кристин Шнайдер. «Формула Excel вычисляет стандартные значения сопротивления 1%».Электронный дизайн, 2002-01-21.[1]

[11] Паркер, Д. Стотт; Eggert, Paul R .; Пирс, Брэд (28 марта 2000). «Арифметика Монте-Карло: основа для статистического анализа ошибок округления». Вычисления IEEE в науке и технике.

[13] Борман, Фил; Чатфилд, Мэрион (10 ноября 2015 г.). «Избегайте опасности использования округленных данных». Журнал фармацевтического и биомедицинского анализа. 115: 506–507. Дои:10.1016 / j.jpba.2015.07.021. PMID 26299526.

[14] Дебора Р. Хенслер (2000). Дилеммы коллективного иска: преследование общественных целей ради личной выгоды. РЭНД. стр.255–293. ISBN 0-8330-2601-1.

[15] Сэмюэл А. Фигероа (июль 1995 г.). «Когда двойное округление безобидно?». Информационный бюллетень ACM SIGNUM. ACM. 30 (3): 21–25. Дои:10.1145/221332.221334.

[16] Роджер Голливер (октябрь 1998 г.). «Эффективное создание ортогональных двойных результатов IEEE по умолчанию с использованием расширенного оборудования IEEE» (PDF). Intel.

[17] Мур, Дж. Стротер; Линч, Том; Кауфманн, Мэтт (1996). «Механически проверенное доказательство правильности ядра алгоритма деления с плавающей запятой AMD5K86» (PDF). Транзакции IEEE на компьютерах. 47. CiteSeerX 10.1.1.43.3309. Дои:10.1109/12.713311. Получено 2016-08-02.

[18] Болдо, Сильви; Мелькионд, Гийом (2008). «Эмуляция FMA и правильно округленных сумм: проверенные алгоритмы с округлением до нечетных» (PDF). Транзакции IEEE на компьютерах. 57 (4): 462–471. Дои:10.1109 / TC.2007.70819. Получено 2016-08-02.

[19] "21718 - real.c округление не идеально". gcc.gnu.org.

[20] Кахан, Уильям Мортон. "Слишком умный логарифм". Получено 2008-11-14.

[Muller_2010-21] Мюллер, Жан-Мишель; Брисебар, Николас; де Динешен, Флоран; Жаннерод, Клод-Пьер; Лефевр, Винсент; Мелькионд, Гийом; Revol, Натали; Stehlé, Damien; Торрес, Серж (2010). «Глава 12: Решение дилеммы производителя стола». Справочник по арифметике с плавающей точкой (1-е изд.). Биркхойзер. Дои:10.1007/978-0-8176-4705-6. ISBN 978-0-8176-4704-9. LCCN 2009939668.

[22] "libultim - окончательная библиотека элементарных функций с правильными округлениями".

[23] "libmcr - библиотека элементарных функций с правильными округлениями".

[24] «CRlibm - математическая библиотека с правильным округлением». Архивировано из оригинал на 2016-10-27.

[25] Дункан Дж. Мелвилл. «Глиняная таблетка YBC 7289». 2006 г.

[26] «Вероятность и теория ошибок». Historical.library.cornell.edu.

[27] Черчилль Эйзенхарт (1947). «Влияние округления или группировки данных». В Эйзенхарте; Хастай; Уоллис (ред.). Избранные методы статистического анализа для научных и промышленных исследований, а также производства и управления. Нью-Йорк: Макгроу-Хилл. стр. 187–223. Получено 2014-01-30.

[28] ttp://ec.europa.eu/economy_finance/publications/publication1224_en.pdf

[29] Батен, Йорг (2009). «Количественная оценка грамотности: возрастная куча и история человеческого капитала» (PDF). Журнал экономической истории. 69 (3): 783–808. Дои:10.1017 / S0022050709001120. HDL:10230/481.

[30] «Спецификация языка ECMA-262 ECMAScript» (PDF). ecma-international.org.

[31] OFCM, 2005 г .: Федеральный метеорологический справочник № 1 В архиве 1999-04-20 на Wayback Machine, Вашингтон, округ Колумбия, 104 с.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[nb 1]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[19]

[20]

[21]

[22]

[23]

[24]

[25]

[26]

[27]

[28]

[29]

[30]