IEEE 754 - IEEE 754
В Стандарт IEEE для арифметики с плавающей запятой (IEEE 754) это технический стандарт за арифметика с плавающей запятой учреждена в 1985 г. Институт инженеров по электротехнике и электронике (IEEE). Стандарт решил много проблем обнаружены в различных реализациях с плавающей запятой, что затрудняло их надежное использование и портативный. Много оборудования единицы с плавающей запятой используйте стандарт IEEE 754.
Стандарт определяет:
- арифметические форматы: наборы двоичный и десятичная дробь данные с плавающей запятой, которые состоят из конечных чисел (включая подписанные нули и субнормальные числа ), бесконечности, а также специальные "не числовые" значения (NaNs )
- форматы обмена: кодировки (битовые строки), которые могут использоваться для обмена данными с плавающей запятой в эффективной и компактной форме
- правила округления: свойства, которые должны выполняться при округлении чисел во время арифметических операций и преобразований
- операции: арифметические и другие операции (например, тригонометрические функции ) по арифметическим форматам
- Обработка исключений: признаки исключительных условий (например, деление на ноль, переполнение, и т.п.)
IEEE 754-2008, опубликованный в августе 2008 г., включает почти все оригинальные IEEE 754-1985 стандарт, плюс Стандарт IEEE 854-1987 на основную независимую арифметику с плавающей запятой. Текущая версия IEEE 754-2019 была опубликована в июле 2019 года.[1] Это небольшая доработка предыдущей версии, включающая в основном уточнения, исправления дефектов и новые рекомендуемые операции.
Стандартная разработка
Первый стандарт арифметики с плавающей запятой, IEEE 754-1985, был опубликован в 1985 году. Он охватывал только двоичную арифметику с плавающей запятой.
Новая версия, IEEE 754-2008, был опубликован в августе 2008 года после семилетнего пересмотра под председательством Дэна Зураса и редактором Майк Коулишоу. Он заменил IEEE 754-1985 (двоичная арифметика с плавающей запятой) и Стандарт IEEE 854-1987 на основную независимую арифметику с плавающей запятой. Двоичные форматы исходного стандарта включены в этот новый стандарт вместе с тремя новыми базовыми форматами, одним двоичным и двумя десятичными. Чтобы соответствовать текущему стандарту, реализация должна реализовывать по крайней мере один из основных форматов как арифметический формат и как формат обмена.
Международный стандарт ISO / IEC / IEEE 60559: 2011 (с содержанием, идентичным IEEE 754-2008) был одобрен для принятия через JTC1 / SC 25 в соответствии с соглашением ISO / IEEE PSDO[2] и опубликовано.[3]
Текущая версия IEEE 754-2019, опубликованная в июле 2019 года, является производной и заменяет IEEE 754-2008 после процесса пересмотра, начатого в сентябре 2015 года под председательством Дэвида Г. Хау и отредактированным Майком Коулишоу. Он включает в себя в основном пояснения (например, totalOrder) и исправления дефектов (например, minNum), но также включает некоторые новые рекомендуемые операции (например, дополненное дополнение).[4][5]
Международный стандарт ИСО / МЭК 60559: 2020 (с содержанием, идентичным IEEE 754-2019) был одобрен для принятия через JTC1 / SC 25 и опубликовано.[6]
Форматы
IEEE 754 формат представляет собой «набор представлений числовых значений и символов». Формат также может включать способ кодирования набора.[7]
Формат с плавающей запятой определяется следующим образом:
- база (также называемая основание) б, который равен 2 (двоичный) или 10 (десятичный) в IEEE 754;
- точность п;
- диапазон экспоненты от Эмин к emax, с участием Эмин = 1 − emax для всех форматов IEEE 754.
Формат включает:
- Конечные числа, которые можно описать тремя целыми числами: s = а знак (ноль или один), c = а значимое (или же коэффициент) имея не более п цифры при записи в базе б (т.е. целое число в диапазоне от 0 до бп - 1), и q = an показатель степени такой, что Эмин ≤ q + п − 1 ≤ emax. Числовое значение такого конечного числа равно (−1)s × c × бq.[а] Кроме того, есть два нулевых значения, которые называются подписанные нули: бит знака определяет, равен ли ноль +0 (положительный ноль) или -0 (отрицательный ноль).
- Две бесконечности: + ∞ и −∞.
- Два вида NaN (не-число): тихий NaN (qNaN) и сигнальный NaN (sNaN).
Например, если б = 10, п = 7 и emax = 96, тогда Эмин = −95, мантисса удовлетворяет 0 ≤ c ≤ 9999999, а показатель степени равен −101 ≤ q ≤ 90. Следовательно, наименьшее ненулевое положительное число, которое может быть представлено, равно 1 × 10−101, а наибольшее - 9999999 × 1090 (9.999999×1096), поэтому полный диапазон чисел равен −9,999999 × 1096 через 9.999999 × 1096. Цифры -б1−emax и б1−emax (здесь −1 × 10−95 и 1 × 10−95) являются самыми маленькими (по величине) нормальные числа; ненулевые числа между этими наименьшими числами называются субнормальные числа.
Представление и кодирование в памяти
Некоторые числа могут иметь несколько возможных представлений в экспоненциальном формате. Например, если б = 10 и п = 7, то −12,345 можно представить как −12345 × 10−3, −123450×10−4, и −1234500 × 10−5. Однако для большинства операций, таких как арифметические операции, результат (значение) не зависит от представления входных данных.
Для десятичных форматов допустимо любое представление, и набор этих представлений называется когорта. Если результат может иметь несколько представлений, стандарт определяет, какой член когорты выбран.
Для двоичных форматов представление становится уникальным путем выбора наименьшего представимого показателя степени, позволяющего точно представить значение. Кроме того, показатель степени не представлен напрямую, но добавляется смещение, так что наименьший представимый показатель степени представлен как 1, а 0 используется для субнормальных чисел. Для чисел с показателем степени в нормальном диапазоне (поле показателя не может содержать ни все единицы, ни все нули), ведущий бит мантиссы всегда будет равен 1. Следовательно, ведущая единица может подразумеваться, а не присутствовать явно в кодировании памяти, а по стандарту явно представленная часть мантиссы будет находиться между 0 и 1. Это правило называется соглашение о начальных битах, неявное соглашение о битах, или же соглашение о скрытых битах. Это правило позволяет двоичному формату иметь дополнительную точность. Соглашение о начальных битах не может использоваться для субнормальных чисел, так как они имеют показатель степени за пределами диапазона нормального показателя и масштабируются по наименьшей представленной экспоненте, как используется для наименьших нормальных чисел.
Из-за возможности нескольких кодировок (по крайней мере, в форматах, называемых форматы обмена), NaN может нести другую информацию: знаковый бит (который не имеет значения, но может использоваться некоторыми операциями) и полезная нагрузка, который предназначен для диагностической информации, указывающей на источник NaN (но полезная нагрузка может иметь другое использование, например NaN-бокс[8][9][10]).
Базовые и обменные форматы
Стандарт определяет пять основных форматов, названных по их числовой базе и количеству битов, используемых при их обменном кодировании. Существует три основных двоичных формата с плавающей запятой (с 32-, 64- или 128-битной кодировкой) и два основных десятичных формата с плавающей запятой (с 64- или 128-битной кодировкой). В двоичный32 и двоичный64 форматы не замужем и двойной форматы IEEE 754-1985 соответственно. Соответствующая реализация должна полностью реализовывать хотя бы один из основных форматов.
Стандарт также определяет форматы обмена, которые обобщают эти основные форматы.[11] Для двоичных форматов требуется соглашение о начальных битах. В следующей таблице приведены самые маленькие форматы обмена (включая основные).
| имя | Распространенное имя | База | Значимые биты[b] или цифры | Десятичные цифры | Биты экспоненты | Десятичный E макс. | Экспонентное смещение[12] | E мин | E макс | Примечания |
|---|---|---|---|---|---|---|---|---|---|---|
| двоичный16 | Половинная точность | 2 | 11 | 3.31 | 5 | 4.51 | 24−1 = 15 | −14 | +15 | не базовый |
| двоичный32 | Одинарная точность | 2 | 24 | 7.22 | 8 | 38.23 | 27−1 = 127 | −126 | +127 | |
| двоичный64 | Двойная точность | 2 | 53 | 15.95 | 11 | 307.95 | 210−1 = 1023 | −1022 | +1023 | |
| двоичный128 | Четверная точность | 2 | 113 | 34.02 | 15 | 4931.77 | 214−1 = 16383 | −16382 | +16383 | |
| двоичный256 | Восьмеричная точность | 2 | 237 | 71.34 | 19 | 78913.2 | 218−1 = 262143 | −262142 | +262143 | не базовый |
| десятичный32 | 10 | 7 | 7 | 7.58 | 96 | 101 | −95 | +96 | не базовый | |
| десятичный64 | 10 | 16 | 16 | 9.58 | 384 | 398 | −383 | +384 | ||
| десятичный128 | 10 | 34 | 34 | 13.58 | 6144 | 6176 | −6143 | +6144 |
Обратите внимание, что в приведенной выше таблице минимальные показатели указаны для нормальных чисел; специальный субнормальное число представление позволяет представлять даже меньшие числа (с некоторой потерей точности). Например, наименьшее положительное число, которое может быть представлено в двоичном формате 64, равно 2.−1074; вклады в число −1074 включают значение E min −1022 и все, кроме одного, из 53 битов значений (2−1022 − (53 − 1) = 2−1074).
Десятичные цифры цифры × журнал10 основание. Это дает приблизительную точность в количестве десятичных цифр.
Десятичное E макс. Emax × журнал10 основание. Это дает приблизительное значение максимального десятичного показателя степени.
Форматы binary32 (одиночный) и binary64 (двойной) - два наиболее распространенных формата, используемых сегодня. На рисунке ниже показана абсолютная точность для обоих форматов в диапазоне значений. Этот рисунок может использоваться для выбора подходящего формата с учетом ожидаемого значения числа и требуемой точности.
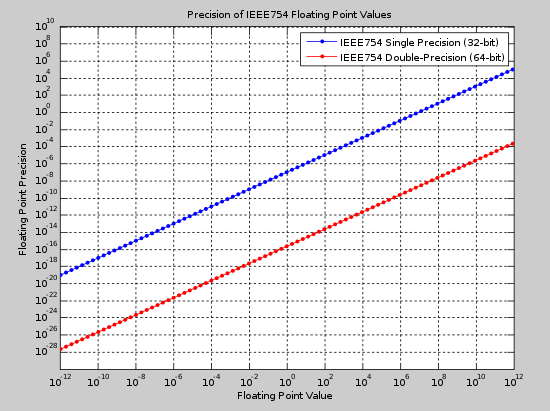
Пример макета для 32-битная плавающая точка является

Расширенные и расширяемые форматы точности
Стандарт определяет необязательные расширенный и форматы с расширяемой точностью, которые обеспечивают большую точность, чем базовые форматы.[13] Формат расширенной точности расширяет базовый формат за счет большей точности и большего диапазона экспонент. Расширяемый формат точности позволяет пользователю определять точность и диапазон экспоненты. Реализация может использовать любое внутреннее представление, выбранное для таких форматов; все, что необходимо определить, это его параметры (б, п, и emax). Эти параметры однозначно описывают набор конечных чисел (комбинации знака, значащей и экспоненты для данного основания системы счисления), которые он может представлять.
Стандарт рекомендует, чтобы языковые стандарты предусматривали метод определения п и emax для каждой поддерживаемой базы б.[14] Стандарт рекомендует, чтобы языковые стандарты и реализации поддерживали расширенный формат, который имеет большую точность, чем самый большой базовый формат, поддерживаемый для каждой системы счисления. б.[15] Для расширенного формата с точностью между двумя основными форматами диапазон экспоненты должен быть таким же большим, как и у следующего более широкого базового формата. Так, например, 64-битное двоичное число с расширенной точностью должно иметь emax не менее 16383. x87 80-битный расширенный формат соответствует этому требованию.
Форматы обмена
Форматы обмена предназначены для обмена данными с плавающей запятой с использованием битовой строки фиксированной длины для данного формата.
Двоичный
Для обмена двоичными числами с плавающей запятой, форматы обмена длиной 16 бит, 32 бита, 64 бита и любое кратное 32 бит ≥ 128[c] определены. 16-битный формат предназначен для обмена или хранения небольших чисел (например, для графики).
Схема кодирования для этих форматов двоичного обмена такая же, как и в IEEE 754-1985: бит знака, за которым следует ш биты экспоненты, которые описывают смещение экспоненты предвзятость, и п - 1 бит, описывающий значение. Ширина поля экспоненты для k-битовый формат вычисляется как ш = круглый (4 журнала2(k)) - 13. Существующие 64- и 128-битные форматы следуют этому правилу, но 16- и 32-битные форматы имеют больше битов экспоненты (5 и 8 соответственно), чем дает эта формула (3 и 7 соответственно).
Как и в стандарте IEEE 754-1985, поле смещенной экспоненты заполняется всеми 1 битами, чтобы указать либо бесконечность (конечное поле значимости = 0), либо NaN (конечное поле значимости ≠ 0). Для NaN, тихие NaN и сигнальные NaN различаются исключительно использованием самого старшего бита конечного поля значимости,[d] а полезная нагрузка переносится в оставшихся битах.
Десятичная дробь
Для обмена десятичными числами с плавающей запятой определены форматы обмена, кратные 32 битам. Как и в случае двоичного обмена, схема кодирования для форматов десятичного обмена кодирует знак, показатель степени и значение. Определены две разные кодировки битового уровня, и обмен затруднен тем фактом, что может потребоваться некоторый внешний индикатор используемой кодировки.
Эти две опции позволяют кодировать мантиссу как сжатую последовательность десятичных цифр, используя плотно упакованная десятичная дробь или, альтернативно, как двоичное целое число. Первый более удобен для прямой аппаратной реализации стандарта, а второй больше подходит для программной эмуляции на двоичном компьютере. В любом случае набор чисел (комбинации знака, значения и экспоненты), который может быть закодирован, идентичен, и особые ценности (± ноль с минимальным показателем степени, ± бесконечность, тихие NaN и сигнальные NaN) имеют идентичное кодирование.
Правила округления
Стандарт определяет пять правил округления. Первые два правила округляются до ближайшего значения; остальные называются направленные округления:
Округление до ближайшего
- Округлить до ближайшего, привязать к четному - округляет до ближайшего значения; если число выпадает на полпути, оно округляется до ближайшего значения с четной младшей цифрой; это значение по умолчанию для двоичных чисел с плавающей запятой и рекомендованное значение по умолчанию для десятичных.
- Округлить до ближайшего, от нуля до нуля - округляет до ближайшего значения; если число падает на полпути, оно округляется до ближайшего значения выше (для положительных чисел) или ниже (для отрицательных чисел); это предназначено как опция для десятичных чисел с плавающей запятой.
Направленные округления
- Округлить в сторону 0 - направленное округление к нулю (также известное как усечение).
- Округлить в сторону + ∞ - направленное округление в сторону положительной бесконечности (также известное как округления или потолок).
- Округлить в сторону −∞ - направленное округление в сторону отрицательной бесконечности (также известное как округление в меньшую сторону или этаж).
| Режим | Пример значения | |||
|---|---|---|---|---|
| +11.5 | +12.5 | −11.5 | −12.5 | |
| до ближайшего, привязки к четному | +12.0 | +12.0 | −12.0 | −12.0 |
| до ближайшего, привязки от нуля | +12.0 | +13.0 | −12.0 | −13.0 |
| к 0 | +11.0 | +12.0 | −11.0 | −12.0 |
| в сторону + ∞ | +12.0 | +13.0 | −11.0 | −12.0 |
| в сторону −∞ | +11.0 | +12.0 | −12.0 | −13.0 |
Если не указано иное, результат операции с плавающей запятой определяется путем применения функции округления к бесконечно точному (математическому) результату. Такая операция называется правильно округленный. Это требование называется правильное округление.[16]
Необходимые операции
Обязательные операции для поддерживаемого арифметического формата (включая основные форматы) включают:
- Арифметические операции (сложение, вычитание, умножение, деление, квадратный корень, слитное умножение – сложение, остаток)[17][18]
- Преобразования (между форматами, в и из строк, и т.п.)[19][20]
- Масштабирование и (для десятичных) квантование[21][22]
- Копирование и изменение знака (абс, отрицание, и т.п.)[23]
- Сравнения и общий заказ[24][25]
- Классификация и тестирование NaN, и т.п.[26]
- Тестирование и установка флагов[27]
- Разные операции.[указывать ]
Предикаты сравнения
Стандарт предоставляет предикаты сравнения для сравнения одного элемента данных с плавающей запятой с другим в поддерживаемом арифметическом формате.[28] Любое сравнение с NaN считается неупорядоченным. −0 и +0 сравниваются как равные.
Предикат общего порядка
Стандарт предоставляет предикат totalOrder, что определяет общий заказ на канонических членах поддерживаемого арифметического формата.[29] Предикат согласуется с предикатами сравнения, когда одно число с плавающей запятой меньше другого. В totalOrder предикат не устанавливает полного порядка для всех кодировок в формате. В частности, он не делает различий между разными кодировками одного и того же представления с плавающей запятой, как когда одна или обе кодировки являются неканоническими.[30] IEEE 754-2019 включает пояснения totalOrder.
Обработка исключений
Стандарт определяет пять исключений, каждое из которых возвращает значение по умолчанию и имеет соответствующий флаг состояния, который поднимается при возникновении исключения.[e] Никакой другой обработки исключений не требуется, но рекомендуются дополнительные альтернативы не по умолчанию (см. § Альтернативная обработка исключений ).
Пять возможных исключений:
- Неверная операция: математически не определено, например, квадратный корень из отрицательного числа. По умолчанию возвращает qNaN.
- Деление на ноль: операция с конечными операндами дает точный бесконечный результат, например, 1/0 или log (0). По умолчанию возвращает ± бесконечность.
- Переполнение: результат слишком велик для правильного представления (т.е., его показатель степени с неограниченным диапазоном показателей будет больше, чем emax). По умолчанию возвращает ± бесконечность для режимов округления до ближайшего (и следует правилам округления для режимов направленного округления).
- Недополнение: результат очень мал (вне нормального диапазона) и неточен. По умолчанию возвращает субнормальный или ноль (согласно правилам округления).
- Неточно: точное (т.е., неокругленный) результат не представляется точно. По умолчанию возвращает правильно округленный результат.
Это те же пять исключений, которые определены в IEEE 754-1985, но деление на ноль Исключение было распространено на операции, отличные от подразделения.
Для десятичных чисел с плавающей запятой есть дополнительные исключения:[31][32]
- Фиксировано: показатель степени результата слишком велик для формата назначения. По умолчанию к коэффициенту добавляются завершающие нули, чтобы уменьшить показатель степени до наибольшего полезного значения. Если это невозможно (потому что это приведет к тому, что количество цифр должно быть больше, чем формат назначения), возникает исключение переполнения.
- Округлено: для коэффициента результата требуется больше цифр, чем предоставляет формат назначения. Если отбрасываются любые ненулевые цифры, сигнализируется неточное исключение.
Кроме того, такие операции, как квантование, когда один из операндов бесконечен или когда результат не соответствует формату назначения, также будут сигнализировать об исключении недопустимой операции.[33]
Рекомендации
Альтернативная обработка исключений
Стандарт рекомендует необязательную обработку исключений в различных формах, включая предварительную подстановку значений по умолчанию, определенных пользователем, и ловушек (исключения, которые каким-либо образом изменяют поток управления) и другие модели обработки исключений, которые прерывают поток, например try / catch. Ловушки и другие механизмы исключения остаются необязательными, как в IEEE 754-1985.
Рекомендуемые операции
В разделе 9 стандарта рекомендуются дополнительные математические операции.[34] что языковые стандарты должны определять.[35] Ничего не требуется для соответствия стандарту.
Рекомендуемые арифметические операции, которые необходимо правильно округлить:[36]
- , ,
- , ,
- , ,
- , ,
- ,
- , ,
- , , ,
- , , (смотрите также: Кратные π )
- , , , (смотрите также: Кратные π )
- , ,
- , ,
В asinPi, acosPi и tanPi функции не были частью стандарта IEEE 754-2008, потому что считалось, что они менее необходимы.[37] Первые два хотя бы упоминались в абзаце, но это было расценено как ошибка.[4] пока они не были добавлены в редакцию 2019 года.
Операции также включают установку и доступ к направлению округления в динамическом режиме,[38] и операции уменьшения вектора, определенные реализацией, такие как сумма, масштабируемое произведение и скалярное произведение, точность которого не указана стандартом.[39]
По состоянию на 2019 год расширенные арифметические операции[40] для двоичных форматов также рекомендуется. Эти операции, указанные для сложения, вычитания и умножения, производят пару значений, состоящую из результата, правильно округленного до ближайшего в формате, и члена ошибки, который можно точно представить в формате. На момент публикации стандарта аппаратные реализации не были известны, но очень похожие операции уже были реализованы в программном обеспечении с использованием хорошо известных алгоритмов. История и мотивация их стандартизации объясняются в справочном документе.[41][42]
По состоянию на 2019 год ранее требовалось minNum, maxNum, minNumMag и maxNumMag в IEEE 754-2008 теперь удалены из-за их неассоциативности. Вместо этого два комплекта новых минимальные и максимальные операции[43] рекомендуются. Первый набор содержит минимальное, минимальное число, максимальное и максимальное число. Второй набор содержит minimumMagnitude, minimumMagnitudeNumber, maximumMagnitude и maximumMagnitudeNumber. История и мотивация этого изменения объясняются в справочном документе.[44]
Оценка выражения
Стандарт рекомендует, как стандарты языка должны определять семантику последовательностей операций, и указывает на тонкости буквальных значений и оптимизаций, которые изменяют значение результата. Напротив, предыдущий 1985 Версия стандарта оставила аспекты языкового интерфейса неопределенными, что привело к несогласованному поведению между компиляторами или различным уровням оптимизации в одном компиляторе.
Языки программирования должны позволять пользователю указывать минимальную точность для промежуточных вычислений выражений для каждого основания. В стандарте это называется «предпочтительной шириной», и должна быть возможность устанавливать ее для каждого блока. Промежуточные вычисления в выражениях должны быть рассчитаны, а любые временные значения должны быть сохранены с использованием максимальной ширины операндов и предпочтительной ширины, если она установлена. Так, например, компилятор, ориентированный на x87 аппаратные средства с плавающей запятой должны иметь средства указания, что промежуточные вычисления должны использовать дважды расширенный формат. Сохраненное значение переменной должно всегда использоваться при вычислении последующих выражений, а не любого предшественника до округления и присвоения переменной.
Воспроизводимость
IEEE 754-1985 допускает множество вариантов реализации (например, кодирование некоторых значений и обнаружение определенных исключений). IEEE 754-2008 усилил многие из них, но несколько вариантов все еще остаются (особенно для двоичных форматов). Пункт о воспроизводимости рекомендует, чтобы языковые стандарты предоставляли средства для написания воспроизводимых программ (т. Е. Программ, которые будут давать одинаковый результат во всех реализациях языка), и описывает, что необходимо сделать для достижения воспроизводимых результатов.
Представление персонажа
Стандарт требует операций для преобразования между основными форматами и внешняя последовательность символов форматы.[45] Преобразование в формат десятичных символов и обратно требуется для всех форматов. Преобразование во внешнюю последовательность символов должно быть таким, чтобы обратное преобразование с округлением до четного восстановило исходное число. Нет требования сохранять полезную нагрузку в виде тихого NaN или сигнального NaN, а преобразование из внешней последовательности символов может превратить сигнальный NaN в тихий NaN.
Исходное двоичное значение будет сохранено путем преобразования в десятичное и обратно с использованием:[46]
- 5 десятичных цифр для двоичного 16,
- 9 десятичных цифр для binary32,
- 17 десятичных цифр для binary64,
- 36 десятичных цифр для двоичного 128.
Для других двоичных форматов необходимое количество десятичных цифр равно
где п - количество значащих битов в двоичном формате, например 237 бит для двоичного кода 256.
(Примечание: в качестве ограничения реализации правильное округление гарантируется только для количества десятичных цифр выше плюс 3 для наибольшего поддерживаемого двоичного формата. Например, если binary32 является наибольшим поддерживаемым двоичным форматом, то преобразование из десятичной внешней последовательности с 12 десятичных цифр гарантированно будут правильно округлены при преобразовании в binary32; но преобразование последовательности из 13 десятичных цифр - нет; однако стандарт рекомендует, чтобы реализации не налагали такого ограничения.)
При использовании десятичного формата с плавающей запятой десятичное представление будет сохранено с использованием:
- 7 десятичных цифр для decimal32,
- 16 десятичных цифр для decimal64,
- 34 десятичных цифры для decimal 128.
Алгоритмы с кодом для правильно округленного преобразования из двоичного в десятичное и из десятичного в двоичное обсуждают Гей,[47] а для тестирования - Паксоном и Каханом.[48]
Смотрите также
- Binade
- Сопроцессор
- C99 для примеров кода, демонстрирующих доступ и использование функций IEEE 754.
- Арифметика с плавающей точкой, для истории, обоснования дизайна и примера использования функций IEEE 754.
- Арифметика с фиксированной точкой, для альтернативного подхода при вычислении с рациональными числами (особенно полезно, когда диапазон экспоненты известен, фиксирован или ограничен во время компиляции).
- IBM System z9, первый процессор, реализующий десятичную арифметику IEEE 754-2008 (с использованием аппаратного микрокода).
- IBM z10, IBM z196, IBM zEC12, и IBM z13, Процессоры, которые полностью реализуют десятичную арифметику IEEE 754-2008 аппаратно.
- ISO / IEC 10967, независимая от языка арифметика (LIA).
- Minifloat, двоичные форматы с плавающей запятой низкой точности, соответствующие принципам IEEE 754.
- МОЩНОСТЬ6, МОЩНОСТЬ7, и МОЩНОСТЬ8 Процессоры, которые полностью аппаратно реализуют десятичную арифметику IEEE 754-2008.
- strictfp, ключевое слово в Язык программирования Java который ограничивает арифметические операции одинарной и двойной точностью IEEE 754, чтобы гарантировать воспроизводимость на обычных аппаратных платформах.
- Дилемма изготовителя стола для получения дополнительной информации о правильном округлении функций.
- Стандартная среда Apple Numerics
- Коническая плавающая точка
Примечания
- ^ Например, если основание равно 10, знак равен 1 (обозначает отрицательное значение), мантисса равна 12345, а показатель степени равен −3, то значение числа равно (−1)1 × 12345 × 10−3 = −1 × 12345 × 0.001 = −12.345.
- ^ включая неявный бит (который всегда равен 1 для нормальных чисел и 0 для субнормальных чисел. Этот неявный бит не сохраняется в памяти), но не знаковый бит.
- ^ В отличие от десятичного, двоичного формата обмена длиной 96 бит не существует. Однако такой формат все еще разрешен как формат без обмена.
- ^ Стандарт рекомендует 0 для сигнализации NaN, 1 для тихих NaN, так что сигнализация NaN может быть заморожена путем изменения только этого бита на 1, в то время как обратное может привести к кодированию бесконечности.
- ^ В некоторых случаях недостаточного заполнения флаг не поднимается.
Рекомендации
- ^ IEEE 754 2019
- ^ «FW: ISO / IEC / IEEE 60559 (IEEE Std 754-2008)». grouper.ieee.org. Архивировано из оригинал на 2017-10-27. Получено 2018-04-04.
- ^ «ISO / IEC / IEEE 60559: 2011 - Информационные технологии - Микропроцессорные системы - Арифметика с плавающей запятой». www.iso.org. Получено 2018-04-04.
- ^ а б Коулишоу, Майк (13 ноября 2013). «Опечатки IEEE 754-2008». speleotrove.com. Получено 2020-01-24.
- ^ «Пересмотр ANSI / IEEE Std 754-2008». ucbtest.org. Получено 2018-04-04.
- ^ «ISO / IEC 60559: 2020 - Информационные технологии - Микропроцессорные системы - Арифметика с плавающей запятой». www.iso.org. Получено 2020-10-25.
- ^ IEEE 754 2008 г., §2.1.27.
- ^ "Внутренности SpiderMonkey". developer.mozilla.org. Получено 2018-03-11.
- ^ Клеменс, Бен (сентябрь 2014 г.). 21st Century C: C Советы от новой школы. O'Reilly Media, Incorporated. п. 160. ISBN 9781491904442. Получено 2018-03-11.
- ^ "zuiderkwast / nanbox: NaN-бокс в C". GitHub. Получено 2018-03-11.
- ^ IEEE 754 2008 г., §3.6.
- ^ Cowlishaw, Майк. «Десятичные арифметические кодировки» (PDF). IBM. Получено 2015-08-06.
- ^ IEEE 754 2008 г., §3.7.
- ^ IEEE 754 2008 г. В §3.7 говорится: «Языковые стандарты должны определять механизмы, поддерживающие расширяемую точность для каждого поддерживаемого основания».
- ^ IEEE 754 2008 г., §3.7 гласит: «Языковые стандарты или реализации должны поддерживать формат расширенной точности, который расширяет самый широкий базовый формат, поддерживаемый в этой системе счисления».
- ^ IEEE 754 2019, §2.1
- ^ IEEE 754 2008 г., §5.3.1
- ^ IEEE 754 2008 г., §5.4.1
- ^ IEEE 754 2008 г., §5.4.2
- ^ IEEE 754 2008 г., §5.4.3
- ^ IEEE 754 2008 г., §5.3.2
- ^ IEEE 754 2008 г., §5.3.3
- ^ IEEE 754 2008 г., §5.5.1
- ^ IEEE 754 2008 г., §5.10
- ^ IEEE 754 2008 г., §5.11
- ^ IEEE 754 2008 г., §5.7.2
- ^ IEEE 754 2008 г., §5.7.4
- ^ IEEE 754 2019, §5.11
- ^ IEEE 754 2019, §5.10
- ^ IEEE 754 2019, §5.10
- ^ «9.4. Decimal - Десятичная арифметика с фиксированной и плавающей запятой - документация Python 3.6.5». docs.python.org. Получено 2018-04-04.
- ^ «Десятичная арифметика - исключительные условия». speleotrove.com. Получено 2018-04-04.
- ^ IEEE 754 2008 г., §7.2 (h)
- ^ IEEE 754 2019, §9.2
- ^ IEEE 754 2008 г., Пункт 9
- ^ IEEE 754 2019, §9.2.
- ^ «Re: Отсутствуют функции tanPi, asinPi и acosPi». grouper.ieee.org. Архивировано из оригинал на 2017-07-06. Получено 2018-04-04.
- ^ IEEE 754 2008 г., §9.3.
- ^ IEEE 754 2008 г., §9.4.
- ^ IEEE 754 2019, §9.5.
- ^ Риди, Джейсон; Деммель, Джеймс. «Расширенные арифметические операции, предлагаемые для IEEE-754 2018» (PDF). 25-я конференция IEEE Symbosium по компьютерной арифметике (ARITH 2018). С. 49–56. В архиве (PDF) из оригинала на 23.07.2019. Получено 2019-07-23.
- ^ «754-я редакция запланирована на 2019 год». 754r.ucbtest.org. Получено 2019-07-23.
- ^ IEEE 754 2019, §9.6.
- ^ Чен, Дэвид. «Удаление операций MinNum и MaxNum из IEEE 754-2019» (PDF). grouper.ieee.org. Получено 2020-02-05.
- ^ IEEE 754 2008 г., §5.12.
- ^ IEEE 754 2008 г., §5.12.2.
- ^ Гей, Дэвид М. (1990-11-30). «Правильно округленные двоично-десятичные и десятично-двоичные преобразования». Рукопись численного анализа. Мерри Хилл, Нью-Джерси, США: AT&T Laboratories. 90-10. Цитировать журнал требует
| журнал =(Помогите) - ^ Паксон, Верн; Кахан, Уильям (1991-05-22). «Программа для тестирования десятичного-двоичного преобразования IEEE». Рукопись. CiteSeerX 10.1.1.144.5889. Цитировать журнал требует
| журнал =(Помогите)
Стандарты
- Компьютерное общество IEEE (29 августа 2008 г.). Стандарт IEEE для арифметики с плавающей запятой. IEEE STD 754-2008. IEEE. С. 1–70. Дои:10.1109 / IEEESTD.2008.4610935. ISBN 978-0-7381-5753-5. IEEE Std 754-2008.
- IEEE Computer Society (22.07.2019). Стандарт IEEE для арифметики с плавающей запятой. IEEE STD 754-2019. IEEE. С. 1–84. Дои:10.1109 / IEEESTD.2019.8766229. ISBN 978-1-5044-5924-2. IEEE Std 754-2019.
- ISO / IEC / IEEE 60559: 2011 - Информационные технологии. Микропроцессорные системы. Арифметика с плавающей запятой.. Iso.org. Июнь 2011. С. 1–58.
- ISO / IEC 60559: 2020 - Информационные технологии. Микропроцессорные системы. Арифметика с плавающей запятой.. Iso.org. Май 2020. С. 1–74.
Вторичные ссылки
- Десятичное число с плавающей точкой арифметика, часто задаваемые вопросы, библиография и ссылки
- Сравнение двоичных чисел с плавающей запятой
- Справочный материал IEEE 754
- IEEE 854-1987 - История и минуты
- Дополнительные чтения для IEEE 754. Включает исторические перспективы.
дальнейшее чтение
- Гольдберг, Дэвид (Март 1991 г.). «Что должен знать каждый компьютерный ученый об арифметике с плавающей точкой». Опросы ACM Computing. 23 (1): 5–48. Дои:10.1145/103162.103163. S2CID 222008826. Получено 2019-03-08.
- Хекер, Крис (Февраль 1996 г.). «Давайте перейдем к (плавающей) точке» (PDF). Журнал разработчиков игр: 19–24. ISSN 1073-922X.
- Северанс, Чарльз (март 1998 г.). "IEEE 754: Интервью с Уильямом Каханом" (PDF). IEEE Computer. 31 (3): 114–115. Дои:10.1109 / MC.1998.660194. S2CID 33291145. Получено 2019-03-08.
- Коулишоу, Майк (Июнь 2003 г.). «Десятичные числа с плавающей запятой: алгоритм для компьютеров». 16-й симпозиум IEEE по компьютерной арифметике, 2003 г. Протоколы (PDF). Труды 16-го симпозиума IEEE по компьютерной арифметике. Лос-Аламитос, Калифорния: Компьютерное общество IEEE. С. 104–111. Дои:10.1109 / ARITH.2003.1207666. ISBN 978-0-7695-1894-7. S2CID 18713046. Получено 2014-11-14.. (Заметка: Алгоризм это не неправильное написание названия; смотрите также алгоритм.)
- Моннио, Дэвид (май 2008 г.). «Подводные камни проверки вычислений с плавающей запятой». Транзакции ACM по языкам и системам программирования. 30 (3): 1–41. arXiv:cs / 0701192. Дои:10.1145/1353445.1353446. ISSN 0164-0925. S2CID 218578808.: Краткое изложение неинтуитивного поведения операций с плавающей запятой на популярных архитектурах с последствиями для проверки и тестирования программ.
- Мюллер, Жан-Мишель; Бруни, Николас; де Динешен, Флоран; Жаннерод, Клод-Пьер; Джолдес, Миоара; Лефевр, Винсент; Мелькионд, Гийом; Revol, Натали; Торрес, Серж (2018) [2010]. Справочник по арифметике с плавающей точкой (2-е изд.). Биркхойзер. Дои:10.1007/978-3-319-76526-6. ISBN 978-3-319-76525-9.
- Овертон, Майкл Л. (2001). Написано в Курантский институт математических наук, Нью-Йоркский университет, Нью-Йорк, США. Численные вычисления с использованием арифметики с плавающей запятой IEEE (1-е изд.). Филадельфия, США: СИАМ. Дои:10.1137/1.9780898718072. ISBN 978-0-89871-482-1. 978-0-89871-571-2, 0-89871-571-7.
- Клив Молер о числах с плавающей запятой
- Биби, Нельсон Х. Ф. (22 августа 2017 г.). Справочник по вычислению математических функций - Программирование с использованием переносимой программной библиотеки MathCW (1-е изд.). Солт-Лейк-Сити, Юта, США: Springer International Publishing AG. Дои:10.1007/978-3-319-64110-2. ISBN 978-3-319-64109-6. LCCN 2017947446. S2CID 30244721.
- Хаф, Дэвид Г. (декабрь 2019 г.). «Стандарт IEEE 754: один для книг по истории». Компьютер. IEEE. 52 (12): 109–112. Дои:10.1109 / MC.2019.2926614. S2CID 208281213.







































