Atan2 - atan2

atan2 (у, Икс) возвращает угол θ между луч к точке (Икс, у) и положительный Икс ось, ограниченная (−π, π].

График ${\displaystyle \operatorname {atan2} (y,x)}$ над ${\displaystyle y/x}$

В функция ${\displaystyle \operatorname {atan2} (y,x)}$ или же ${\displaystyle \operatorname {arctan2} (y,x)}$ (из "2-аргумент арктангенс ") определяется как угол в Евклидова плоскость, приведены в радианы, между положительными Икс ось и луч к точка (Икс, у) ≠ (0, 0).

Функция ${\displaystyle \operatorname {atan2} (y,x)}$ впервые появился на языке программирования Фортран (в реализации IBM FORTRAN-IV в 1961 году). Первоначально он был предназначен для возврата правильного и однозначного значения угла θ в преобразовании из декартовы координаты (Икс, у) к полярные координаты (р, θ).

Эквивалентно, ${\displaystyle \operatorname {atan2} (y,x)}$ это аргумент (также называемый фаза или же угол) из комплексное число ${\displaystyle x+iy.}$

${\displaystyle \operatorname {atan2} (y,x)}$ возвращает одно значение θ такой, что −π < θ ≤ π и для некоторых р > 0,

${\displaystyle {\begin{aligned}x&=r\cos \theta ,\\y&=r\sin \theta .\end{aligned}}}$

Хотя это правда, что ${\displaystyle r={\sqrt {x^{2}+y^{2}}}}$, не всегда выполняется следующая эквивалентность:

${\displaystyle \theta =\arctan \left({\frac {y}{x}}\right).}$

Это справедливо только тогда, когда Икс > 0. Когда Икс < 0, угол, очевидный из приведенного выше выражения, указывает в направлении, противоположном правильному углу, и значение π (или 180 °) должны быть либо добавлены, либо вычтены из θ поставить декартову точку (Икс, у) в правильный квадрант Евклидова плоскость.^[1] Это требует знания признаков Икс и у отдельно, что означает потерю информации при у делится на Икс.

Поскольку любое целое число, кратное 2π можно добавить к углу θ не меняя ни Икс или же у, подразумевая неоднозначное значение для возвращаемого значения, основная стоимость угла, в интервале (−π, π] возвращается. θ является подписанный, при этом углы против часовой стрелки являются положительными, а по часовой - отрицательными. Конкретно, ${\displaystyle \operatorname {atan2} (y,x)}$ находится в интервал [0, π] когда у ≥ 0, И в (−π, 0) когда у < 0.

История и мотивация

График касательной функции от -π к +π с соответствующими знаками у/Икс. Зеленые стрелки указывают на результаты atan2 (−1, −1) и atan2 (1, 1).

В atan2 функция была впервые представлена ​​в компьютере языки программирования, но теперь это распространено и в других областях науки и техники. Он восходит, по крайней мере, к FORTRAN язык программирования^[2]и в настоящее время встречается во многих современных языки программирования. Среди этих языков: C с math.h стандартная библиотека, то Ява Математическая библиотека, .NET System.Math (можно использовать из C #, VB.NET и др.), Python математический модуль, Рубин Математический модуль, Идти математический пакет^[3] и в другом месте. Кроме того, многие языки сценариев, такие как Perl, включить C-стиль atan2 (у, х) функция.

Единственный аргумент арктангенс функция не может различать диаметрально противоположные направления. Например, угол против часовой стрелки от Икс ось к вектору (1, 1), рассчитывается обычным образом как арктан (1/1), является π / 4 (радианы) или 45°. Однако угол между Икс ось и вектор (−1, −1) тем же способом оказывается арктангенс (-1 / -1), опять таки π / 4, хотя можно было ожидать ответов −3π / 4 (−135 °) или 5π / 4 (225 °). Кроме того, попытка найти угол между Икс ось и векторы (0, у), у ≠ 0 требует оценки арктан (у/0), который не выполняется при делении на ноль.

В atan2 функция вычисляет один уникальный арктангенс значение из двух переменных у и Икс, где приметы обоих аргументов используются для определения квадрант результата, тем самым выбрав нужную ветку арктангенс из у/Икс, например, atan2 (1, 1) = π / 4 и atan2 (−1, −1) = −3π / 4. Аналогично, например, atan2 (1, 0) = π / 2.

Когда вычисления выполняются вручную, необходимые квадрантные корректировки и обработка исключений могут быть выполнены путем проверки, но более полезно иметь единственную функцию, которая всегда дает однозначно правильный результат. atan2 функция полезна во многих приложениях, включающих векторов в Евклидово пространство, например, поиск направления от одной точки к другой. Основное использование - вращение компьютерной графики для преобразования матрица вращения представления в Углы Эйлера.

Определение и расчет

Функция atan2 вычисляет основная стоимость из аргумент функция применяется к комплексное число Икс + уя. То есть, atan2 (у, Икс) = Pr arg (Икс + уi) = Arg (Икс + уя). Аргумент может быть изменен произвольным кратным 2π (соответствует полному повороту вокруг начала координат) без какого-либо различия угла, но для определения atan2 однозначно используется главное значение в классифицировать ${\displaystyle (-\pi ,\pi ]}$, то есть, −π у, Икс) ≤ π.

С точки зрения стандарта арктан функция, диапазон которой (−π / 2, π / 2), это можно выразить следующим образом:

${\displaystyle \operatorname {atan2} (y,x)={\begin{cases}\arctan({\frac {y}{x}})&{\text{if }}x>0,\\\arctan({\frac {y}{x}})+\pi &{\text{if }}x<0{\text{ and }}y\geq 0,\\\arctan({\frac {y}{x}})-\pi &{\text{if }}x<0{\text{ and }}y<0,\\+{\frac {\pi }{2}}&{\text{if }}x=0{\text{ and }}y>0,\\-{\frac {\pi }{2}}&{\text{if }}x=0{\text{ and }}y<0,\\{\text{undefined}}&{\text{if }}x=0{\text{ and }}y=0.\end{cases}}}$

Компактное выражение с четырьмя перекрывающимися полуплоскостями:

${\displaystyle \operatorname {atan2} (y,x)={\begin{cases}\arctan \left({\frac {y}{x}}\right)&{\text{if }}x>0,\\{\frac {\pi }{2}}-\arctan \left({\frac {x}{y}}\right)&{\text{if }}y>0,\\-{\frac {\pi }{2}}-\arctan \left({\frac {x}{y}}\right)&{\text{if }}y<0,\\\arctan \left({\frac {y}{x}}\right)\pm \pi &{\text{if }}x<0,\\{\text{undefined}}&{\text{if }}x=0{\text{ and }}y=0.\end{cases}}}$

В Кронштейн Айверсона нотация позволяет получить еще более компактное выражение:

${\displaystyle \operatorname {atan2} (y,x)}$	${\displaystyle =\arctan \left({\frac {y}{x}}\right)[x\neq 0]+\operatorname {sgn}(y)\left(\pi [x<0]+{\frac {\pi }{2}}[x=0]\right)}$
	${\displaystyle +\;{\text{undefined}}\;\![x=0\wedge y=0]}$ [примечание 1]

Формула без видимого условная конструкция:

${\displaystyle \operatorname {atan2} (y,x)=\operatorname {sgn}(x)^{2}\arctan \left({\frac {y}{x}}\right)+{\frac {1-\operatorname {sgn}(x)}{2}}\left(1+\operatorname {sgn}(y)-\operatorname {sgn}(y)^{2}\right)\pi }$

Следующее выражение получено из формула касательного полуугла также может использоваться для определения atan2:

${\displaystyle \operatorname {atan2} (y,x)={\begin{cases}2\arctan \left({\frac {y}{{\sqrt {x^{2}+y^{2}}}+x}}\right)&{\text{if }}x>0{\text{ or }}y\neq 0,\\\pi &{\text{if }}x<0{\text{ and }}y=0,\\{\text{undefined}}&{\text{if }}x=0{\text{ and }}y=0.\end{cases}}}$

Это выражение может больше подходить для символического использования, чем определение выше. Однако он не подходит для общего плавающая точка вычислительное использование, поскольку эффект ошибок округления в ${\displaystyle {\sqrt {x^{2}+y^{2}}}}$ расширяться рядом с регионом Икс < 0, у = 0 (это может даже привести к разделению у нулем).

Вариант последней формулы, позволяющий избежать этих завышенных ошибок округления:

${\displaystyle \operatorname {atan2} (y,x)={\begin{cases}2\arctan \left({\frac {y}{{\sqrt {x^{2}+y^{2}}}+x}}\right)&{\text{if }}x>0,\\2\arctan \left({\frac {{\sqrt {x^{2}+y^{2}}}-x}{y}}\right)&{\text{if }}x\leq 0{\text{ and }}y\neq 0,\\\pi &{\text{if }}x<0{\text{ and }}y=0,\\{\text{undefined}}&{\text{if }}x=0{\text{ and }}y=0.\end{cases}}}$

Вывод главного значения аргумента относится к этой цифре.

Примечания:

• Это дает результаты в диапазоне (−π, π].^{[заметка 2]}
• Как было сказано выше, главное значение аргумента atan2 (у, Икс) может быть связано с арктан (у/Икс) по тригонометрии. Вывод происходит следующим образом:

Если (Икс, у) = (р потому чтоθ, р грехθ), тогда загар (θ/2) = у / (р + Икс). Следует, что

${\displaystyle {\text{atan2}}(y,x)=\theta =2\,\theta /2=2\arctan {\frac {y}{{\sqrt {x^{2}+y^{2}}}+x}}.}$

Обратите внимание, что √Икс² + у² + Икс ≠ 0 в рассматриваемом домене.

Производная

Дальнейшая информация: Номер обмотки

Поскольку функция atan2 является функцией двух переменных, имеет две частные производные. В точках, где существуют эти производные, atan2 равно, за исключением константы, арктан (у/Икс). Следовательно, для Икс > 0 или же у ≠ 0,

${\displaystyle {\begin{aligned}&{\frac {\partial }{\partial x}}\operatorname {atan2} (y,\,x)={\frac {\partial }{\partial x}}\arctan \left({\frac {y}{x}}\right)=-{\frac {y}{x^{2}+y^{2}}},\\[5pt]&{\frac {\partial }{\partial y}}\operatorname {atan2} (y,\,x)={\frac {\partial }{\partial y}}\arctan \left({\frac {y}{x}}\right)={\frac {x}{x^{2}+y^{2}}}.\end{aligned}}}$

Таким образом градиент atan2 задается

${\displaystyle \nabla {\text{atan2}}(y,x)=\left({-y \over x^{2}+y^{2}},\ {x \over x^{2}+y^{2}}\right).}$

Неформально представляющая функцию atan2 как угловая функция θ(Икс, у) = atan2 (у, Икс) (который определяется только с точностью до константы) дает следующую формулу для полный дифференциал:

${\displaystyle {\begin{aligned}\mathrm {d} \theta &={\frac {\partial }{\partial x}}\operatorname {atan2} (y,\,x)\,\mathrm {d} x+{\frac {\partial }{\partial y}}\operatorname {atan2} (y,\,x)\,\mathrm {d} y\\[5pt]&=-{\frac {y}{x^{2}+y^{2}}}\,\mathrm {d} x+{\frac {x}{x^{2}+y^{2}}}\,\mathrm {d} y.\end{aligned}}}$

Пока функция atan2 прерывистый по отрицательному Икс-ось, отражающая тот факт, что угол не может быть определен непрерывно, эта производная определяется непрерывно, за исключением начала координат, что отражает тот факт, что бесконечно малые (и действительно локальные) изменения in angle может быть определен везде, кроме начала координат. Интегрирование этой производной по траектории дает полное изменение угла по траектории, а интегрирование по замкнутому контуру дает номер намотки.

На языке дифференциальная геометрия, эта производная есть однотипный, и это закрыто (его производная равна нулю), но не точный (это не производная 0-формы, т.е. функция), и фактически она порождает первую когомологии де Рама из проколотый самолет. Это самый простой пример такой формы, и он является фундаментальным в дифференциальной геометрии.

Частные производные от atan2 не содержат тригонометрических функций, что делает его особенно полезным во многих приложениях (например, встроенных системах), где оценка тригонометрических функций может быть дорогостоящей.

Иллюстрации

atan2 для выбранных лучей

На этом рисунке показаны значения atan2 вдоль выбранных лучей от начала координат, отмеченные на единичной окружности. Значения в радианах показаны внутри круга. На диаграмме используется стандартное математическое соглашение, согласно которому углы увеличиваются. против часовой стрелки от нуля по лучу вправо. Обратите внимание, что порядок аргументов обратный; функция atan2 (у, Икс) вычисляет угол, соответствующий точке (Икс, у).

Сравнение арктан и функции atan2

На этом рисунке показаны значения ${\displaystyle \arctan(\tan(\theta ))}$ вместе с ${\displaystyle \operatorname {atan2} (\sin(\theta ),\cos(\theta ))}$ за ${\displaystyle 0\leq \theta \leq 2\pi }$. Обе функции нечетные и периодические с периодами ${\displaystyle \pi }$ и ${\displaystyle 2\pi }$соответственно, и, таким образом, легко дополняется до любой области реальных значений ${\displaystyle \theta }$. Отчетливо видно срезы веток из ${\displaystyle \operatorname {atan2} }$-функция на ${\displaystyle \theta =\pi }$, и из ${\displaystyle \arctan }$-функция на ${\displaystyle \theta \in \{{\tfrac {\pi }{2}},\;{\tfrac {3\pi }{2}}\}}$.^[4]

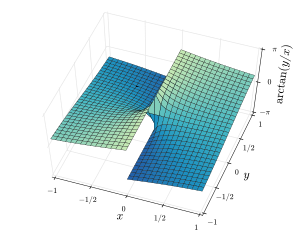
На двух рисунках ниже показаны трехмерные изображения соответственно atan2 (у, Икс) и арктан (у/Икс) над районом плоскости. Обратите внимание, что для atan2 (у, Икс), лучи в Икс/Y-плоскости, исходящие из начала координат, имеют постоянные значения, но для арктан (у/Икс) линии в Икс/Y-плоскости, проходящие через начало координат, имеют постоянные значения. За Икс > 0, две диаграммы дают одинаковые значения.

Сумма углов и идентичность разностей

Основная статья: Список тригонометрических тождеств § Сумма углов и разностные тождества

Суммы ${\displaystyle \operatorname {atan2} }$ может быть свернуто в одну операцию в соответствии со следующим идентификатором

${\displaystyle \operatorname {atan2} (y_{1},x_{1})\pm \operatorname {atan2} (y_{2},x_{2})=\operatorname {atan2} (y_{1}x_{2}\pm y_{2}x_{1},x_{1}x_{2}\mp y_{1}y_{2})}$

...при условии, что ${\displaystyle \operatorname {atan2} (y_{1},x_{1})\pm \operatorname {atan2} (y_{2},x_{2})\in (-\pi ,\pi ]}$.

Доказательство включает рассмотрение двух случаев, в одном из которых ${\displaystyle y_{2}\neq 0}$ или же ${\displaystyle x_{2}>0}$ и тот, где ${\displaystyle y_{2}=0}$ и ${\displaystyle x_{2}<0}$.

Мы рассматриваем только случай, когда ${\displaystyle y_{2}\neq 0}$ или же ${\displaystyle x_{2}>0}$. Для начала сделаем следующие наблюдения:

1. ${\displaystyle -\operatorname {atan2} (y,x)=\operatorname {atan2} (-y,x)}$ при условии, что ${\displaystyle y\neq 0}$ или же ${\displaystyle x>0}$.
2. ${\displaystyle \operatorname {Arg} (x+iy)=\operatorname {atan2} (y,x)}$, куда ${\displaystyle \operatorname {Arg} }$ это функция со сложным аргументом.
3. ${\displaystyle \theta =\operatorname {Arg} e^{i\theta }}$ в любое время ${\displaystyle \theta \in (-\pi ,\pi ]}$, следствие Формула Эйлера.
4. ${\displaystyle \operatorname {Arg} (e^{i\operatorname {Arg} \zeta _{1}}e^{i\operatorname {Arg} \zeta _{2}})=\operatorname {Arg} (\zeta _{1}\zeta _{2})}$.

Чтобы увидеть (4), имеем личность ${\displaystyle e^{i\operatorname {Arg} \zeta }={\bar {\zeta }}}$ куда ${\displaystyle {\bar {\zeta }}=\zeta /\left|\zeta \right|}$, следовательно ${\displaystyle \operatorname {Arg} (e^{i\operatorname {Arg} \zeta _{1}}e^{i\operatorname {Arg} \zeta _{2}})=\operatorname {Arg} ({\bar {\zeta _{1}}}{\bar {\zeta _{2}}})}$. Кроме того, поскольку ${\displaystyle \operatorname {Arg} \zeta =\operatorname {Arg} a\zeta }$ для любого положительного реального значения ${\displaystyle a}$, то если положить ${\displaystyle \zeta =\zeta _{1}\zeta _{2}}$ и ${\displaystyle a={\frac {1}{\left|\zeta _{1}\right|\left|\zeta _{2}\right|}}}$ тогда у нас есть ${\displaystyle \operatorname {Arg} ({\bar {\zeta _{1}}}{\bar {\zeta _{2}}})=\operatorname {Arg} (\zeta _{1}\zeta _{2})}$.

Из этих наблюдений есть следующие эквиваленты:

${\displaystyle {\begin{aligned}\operatorname {atan2} (y_{1},x_{1})\pm \operatorname {atan2} (y_{2},x_{2})&{}=\operatorname {atan2} (y_{1},x_{1})+\operatorname {atan2} (\pm y_{2},x_{2})&{\text{by (1)}}\\&{}=\operatorname {Arg} (x_{1}+iy_{1})+\operatorname {Arg} (x_{2}\pm iy_{2})&{\text{by (2)}}\\&{}=\operatorname {Arg} e^{i(\operatorname {Arg} (x_{1}+iy_{1})+\operatorname {Arg} (x_{2}\pm iy_{2}))}&{\text{by (3)}}\\&{}=\operatorname {Arg} (e^{i\operatorname {Arg} (x_{1}+iy_{1})}e^{i\operatorname {Arg} (x_{2}\pm iy_{2})})\\&{}=\operatorname {Arg} ((x_{1}+iy_{1})(x_{2}\pm iy_{2}))&{\text{by (4)}}\\&{}=\operatorname {Arg} (x_{1}x_{2}\mp y_{1}y_{2}+i(y_{1}x_{2}\pm y_{2}x_{1}))\\&{}=\operatorname {atan2} (y_{1}x_{2}\pm y_{2}x_{1},x_{1}x_{2}\mp y_{1}y_{2})&{\text{by (2)}}\end{aligned}}}$

Следствие: если ${\displaystyle (y_{1},x_{1})}$ и ${\displaystyle (y_{2},x_{2})}$ являются 2-мерными векторами, формула разности часто используется на практике для вычисления угла между этими векторами с помощью ${\displaystyle \operatorname {atan2} }$, так как результирующее вычисление ведет себя нормально в диапазоне ${\displaystyle (-\pi ,\pi ]}$ и поэтому может использоваться без проверки диапазона во многих практических ситуациях.

Реализация функции на общих компьютерных языках

Реализация функции отличается от одного компьютерного языка к другому:

• Функция C atan2, и большинство других компьютерных реализаций, предназначены для уменьшения усилий по преобразованию декартовых координат в полярные и поэтому всегда определяют atan2 (0, 0). На реализациях без подписанный ноль, или, когда задано положительное нулевое значение аргументов, обычно определяется как 0. Он всегда возвращает значение в диапазоне [−π, π] вместо того, чтобы вызывать ошибку или возвращать NaN (Не число).

• В Common Lisp, если существуют необязательные аргументы, загар функция позволяет опционально поставить Икс координата: (загару Икс).^[5]
• В Mathematica, форма ArcTan [Икс, у] используется там, где форма с одним параметром обеспечивает нормальный арктангенс (обратите внимание, что порядок аргументов обратный по сравнению с соглашением, используемым в обсуждении выше). Mathematica классифицирует ArcTan [0, 0] как неопределенное выражение.
• В Майкрософт Эксель,^[6] OpenOffice.org Calc, LibreOffice Calc,^[7] Таблицы Google,^[8] Номера iWork,^[9] и ANSI SQL: стандарт 2008,^[10] то atan2 функция имеет два обратных аргумента.
• в Intel Архитектура код ассемблера, atan2 известен как FPATAN (частичный арктангенс с плавающей запятой) инструкция.^[11] Он может иметь дело с бесконечностями, и результаты лежат в закрытом интервале [−π, π], например atan2 (∞, Икс) = +π/ 2 для конечных Икс. Особенно, FPATAN определяется, когда оба аргумента равны нулю:

  atan2 (+0, +0) = +0;

  atan2 (+0, -0) = +π;

  atan2 (-0, +0) = −0;

  atan2 (-0, -0) = −π.

Это определение связано с концепцией подписанный ноль.

• На большинстве графических калькуляторов TI (за исключением ТИ-85 и ТИ-86 ) эквивалентная функция называется R►Pθ и имеет обратные аргументы.
• На ТИ-85 аргумент функция называется угол (x, y) и хотя кажется, что он принимает два аргумента, на самом деле он имеет только один сложный аргумент, который обозначается парой чисел: Икс + уя = (Икс, у).
• В математических сочинениях, отличных от исходного кода, например в книгах и статьях, обозначения Арктан^[12] и Загар^−1[13] были использованы; это варианты заглавной буквы обычный арктан и загар⁻¹. Это использование согласуется с обозначение сложных аргументов, так что Загар(у, Икс) = Arg (Икс + уя).
• На HP калькуляторов, рассматривайте координаты как комплексное число, а затем возьмите ARG. Или же << C-> R ARG >> 'АТАН2' СТО.
• На научных калькуляторах функцию часто можно рассчитать как угол, заданный при (Икс, у) конвертируется из прямоугольные координаты к полярные координаты.
• Системы, поддерживающие символьную математику, обычно возвращают неопределенное значение для atan2 (0, 0) или иным образом сигнализировать о возникновении ненормального состояния.
• Для систем, реализующих подписанный ноль, бесконечности, или же Не число (Например, IEEE с плавающей точкой ), обычно реализуются разумные расширения, которые могут расширять диапазон производимых значений, включая:π и -0. Они также могут возвращать NaN или вызывать исключение при задании аргумента NaN.
• Для систем, реализующих подписанный ноль (Например, IEEE с плавающей точкой ), atan2 (−0, Икс), Икс <0 представляет риск возврата значения -π, в случае, если реализация atan2 (у, х) не может правильно обработать -0 входов.
• Бесплатная математическая библиотека FDLIBM (свободно распространяемая LIBM) доступна по адресу netlib имеет исходный код, показывающий, как он реализует atan2 включая обработку различных исключительных значений IEEE.
• Для систем без аппаратного умножителя функция atan2 может быть реализован численно надежным способом с помощью КОРДИК метод. Таким образом, реализации загар(у) вероятно, выберет вычислить atan2 (у, 1).

Смотрите также

• гипотеза

Рекомендации

1. http://scipp.ucsc.edu/~haber/ph116A/arg_11.pdf
2. Органик, Эллиотт I. (1966). Праймер FORTRAN IV. Эддисон-Уэсли. п. 42. Некоторые процессоры также предлагают библиотечную функцию ATAN2, функцию двух аргументов (противоположного и смежного).
3. "src / math / atan2.go". Язык программирования Go. Получено 20 апреля 2018.
4. «Вольф Юнг: Мандель, программное обеспечение для сложной динамики». www.mndynamics.com. Получено 20 апреля 2018.
5. «CLHS: функция ASIN, ACOS, ATAN». LispWorks.
6. «Метод Microsoft Excel Atan2». Microsoft.
7. "LibreOffice Calc ATAN2". Libreoffice.org.
8. "Список функций Google Таблиц".
9. «Список тригонометрических функций чисел». Яблоко.
10. «ANSI SQL: стандарт 2008». Терадата. Архивировано из оригинал на 20.08.2015.
11. IA-32 Руководство разработчика программного обеспечения для архитектуры Intel. Том 2A: Справочник по набору команд, A-M, 2004.
12. Бургер, Вильгельм; Бердж, Марк Дж. (7 июля 2010 г.). Принципы обработки цифровых изображений: основные методы. Springer Science & Business Media. ISBN  9781848001916. Получено 20 апреля 2018 - через Google Книги.
13. Глиссон, Тилдон Х. (18 февраля 2011 г.). Введение в анализ и проектирование схем. Springer Science & Business Media. ISBN  9789048194438. Получено 20 апреля 2018 - через Google Книги.

внешняя ссылка

• Онлайн калькулятор ATAN2
• Java 1.6 SE JavaDoc
• atan2 во всем2
• Решение PicBasic Pro atan2 для PIC18F

Другие реализации / код для atan2

• Пеленг между двумя точками
• Арктан и полярные координаты
• Что такое «Арккос»?

Примечания

1. Тем самым

   ${\displaystyle {\text{undefined}}\cdot 0=0,}$

   ${\displaystyle {\text{undefined}}\cdot 1={\text{undefined}}}$ и

   ${\displaystyle z+{\text{undefined}}={\text{undefined}}}$ для каждого ${\displaystyle z.}$

2. Можно применить периодичность результата для сопоставления с другим желаемым диапазоном, например отображение на [0, 2π) добавляя 2π к отрицательным результатам.