История тригонометрии - History of trigonometry
| Тригонометрия |
|---|
 |
| Ссылка |
| Законы и теоремы |
| Исчисление |
Раннее изучение треугольников можно проследить до 2 тысячелетие до нашей эры, в Египетская математика (Математический папирус Райнда ) и Вавилонская математика. Тригонометрия также была распространена в Кушите математика.[1]Систематическое изучение тригонометрический функции начались в Эллинистическая математика, достигнув Индии в рамках Эллинистическая астрономия.[2] В Индийская астрономия, изучение тригонометрических функций процветало в Период Гупта, особенно из-за Арьябхата (шестой век н.э.), который открыл функция синуса. В средние века изучение тригонометрии продолжалось в Исламская математика математиками, такими как Аль-Хорезми и Абу аль-Вафа. Это стало самостоятельной дисциплиной в Исламский мир, где все шесть тригонометрические функции были известны. Переводы арабских и греческих текстов привело к тому, что тригонометрия стала предметом изучения на латинском Западе, начиная с эпоха Возрождения с Региомонтан. Развитие современной тригонометрии сместилось в период западного Эпоха Просвещения, начиная с математики 17 века (Исаак Ньютон и Джеймс Стирлинг ) и достигнув своей современной формы с Леонард Эйлер (1748).
Этимология
Термин «тригонометрия» произошел от Греческий τρίγωνον тригон, "треугольник" и μέτρον метрон, "мера".[3]
Современное слово «синус» происходит от латинский слово синус, что означает «залив», «грудь» или «складка», косвенно, через индийскую, персидскую и арабскую передачи, происходит от греческого термина хорд "тетива, аккорд". Индусский термин для синуса в санскрит является джья "тетива", первоначально введенная индусами, обычно использовала три тригонометрические функции джйа, коти-джйа и уткрама-джйа. Индусы определили их как функции дуги круга, а не угла, отсюда их связь с тетивой лука, и, следовательно, «хорда дуги» для дуги называется «луком» (дхану, чапа). Его синонимы - джива, синджини, маурви, гуна и т. Д. Функция синуса позже была адаптирована в варианте джива.[4]санскрит джива был переведен (принят) на арабский язык как джиба, написано jb جب.[5][6] Затем это было истолковано как подлинное арабское слово Джейб, что означает "грудь, складка, залив",[6] либо арабами, либо ошибкой европейских переводчиков, таких как Роберт Честерский, кто перевел Джейб на латынь как синус.[5] Особенно Фибоначчи с синус прямой мышцы дуги оказал влияние на установление термина синус.[7] Слова «минута» и «секунда» произошли от латинских словосочетаний. partes minutae primae и partes minutae secundae.[8] Это примерно означает «первые маленькие части» и «вторые маленькие части».
Разработка
Древний Ближний Восток
Древний Египтяне и Вавилоняне знал теоремы об отношении сторон подобных треугольников на протяжении многих веков. Однако, поскольку в доэллинских обществах отсутствовала концепция угловой меры, вместо этого они ограничивались изучением сторон треугольников.[9]
В Вавилонские астрономы вел подробные записи о подъеме и закате звезды, движение планеты, а солнечная и лунная затмения, все это требует знания угловатый расстояния, измеренные на небесная сфера.[6] Основываясь на одной интерпретации Плимптон 322 клинопись табличка (ок. 1900 г. до н.э.), некоторые даже утверждали, что у древних вавилонян была таблица секантов.[10] Однако есть много споров относительно того, является ли это таблица Пифагорейские тройки, решение квадратных уравнений, или тригонометрическая таблица.
С другой стороны, египтяне использовали примитивную форму тригонометрии для построения пирамиды во 2 тысячелетии до н. э.[6] В Математический папирус Райнда, написано египетским писцом Ахмес (ок. 1680–1620 гг. до н.э.), содержит следующую задачу, относящуюся к тригонометрии:[6]
"Если высота пирамиды 250 локтей, а длина стороны основания 360 локтей, то какова ее высота?" секед ?"
Решение проблемы, предложенное Ахмесом, - это отношение половины стороны основания пирамиды к ее высоте, или отношение подъема к высоте ее грани. Другими словами, количество, которое он нашел для секед - котангенс угла к основанию пирамиды и ее грани.[6]
Классическая древность
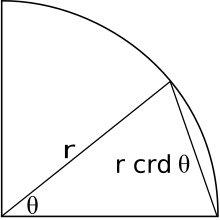
Древний Греческие и эллинистические математики использовал аккорд. Учитывая окружность и дугу на окружности, хорда - это линия, которая образует дугу. Серединный перпендикуляр хорды проходит через центр окружности и делит угол пополам. Одна половина разрезанной пополам хорды - это синус половины разделенного пополам угла, то есть
и, следовательно, синусоидальная функция также известна как полуаккорд. Благодаря этой связи ряд тригонометрических тождеств и теорем, которые известны сегодня, также были известны Эллинистический математики, но в их эквивалентной аккордовой форме.[11]
Хотя тригонометрии в произведениях Евклид и Архимед, в строгом смысле этого слова, есть теоремы, представленные в геометрическом (а не тригонометрическом) виде, которые эквивалентны определенным тригонометрическим законам или формулам.[9] Например, предложения двенадцать и тринадцать второй книги Элементы являются законы косинусов для тупых и острых углов соответственно. Теоремы о длинах хорд являются приложениями закон синуса. А теорема Архимеда о сломанных хордах эквивалентна формулам для синусов сумм и разностей углов.[9] Чтобы компенсировать отсутствие таблица аккордов, математики Аристарх время иногда использовало утверждение, что в современных обозначениях грехα/ грехβ < α/β <загарα/ загарβ всякий раз, когда 0 ° <β <α <90 °, теперь известно как Неравенство Аристарха.[12]
Первую тригонометрическую таблицу, по-видимому, составил Гиппарх из Никее (180 - 125 г. до н. Э.), Который теперь известен как «отец тригонометрии».[13] Гиппарх был первым, кто ввел в таблицу соответствующие значения дуги и хорды для ряда углов.[7][13]
Хотя неизвестно, когда систематическое использование круга 360 ° вошло в математику, известно, что систематическое введение круга 360 ° произошло немного позже. Аристарх Самосский составлен О размерах и расстояниях Солнца и Луны (ок. 260 г. до н.э.), поскольку он измерял угол в долях квадранта.[12] Кажется, что систематическое использование круга 360 ° во многом обязано Гиппарху и его таблица аккордов. Гиппарх, возможно, заимствовал идею этого разделения из Гипсикл кто ранее разделил день на 360 частей, такое деление дня, возможно, было предложено вавилонской астрономией.[14] В древней астрономии зодиак делился на двенадцать «знаков» или тридцать шесть «деканов». Сезонный цикл, составляющий примерно 360 дней, мог бы соответствовать знакам и деканам зодиака, если бы каждый знак был разделен на тридцать частей, а каждый декан - на десять частей.[8] Это связано с вавилонским шестидесятеричный система счисления что каждый градус делится на шестьдесят минут, а каждая минута делится на шестьдесят секунд.[8]
Менелай Александрийский (около 100 г. н.э.) написал в трех книгах Sphaerica. В Книге I он установил основу для сферических треугольников, аналогичную евклидовой основе для плоских треугольников.[11] Он устанавливает теорему, которая не имеет евклидова аналога, что два сферических треугольника конгруэнтны, если соответствующие углы равны, но он не различал конгруэнтные и симметричные сферические треугольники.[11] Другая теорема, которую он устанавливает, заключается в том, что сумма углов сферического треугольника больше 180 °.[11] Книга II Sphaerica применяет сферическую геометрию к астрономии. А в третьей книге содержится «теорема Менелая».[11] Далее он привел свое знаменитое «правило шести величин».[15]
Потом, Клавдий Птолемей (ок. 90 - ок. 168 г. н.э.) расширились на Гиппарха. Аккорды по кругу в его Альмагест, или Математический синтаксис. Альмагест - это в первую очередь работа по астрономии, а астрономия опирается на тригонометрию. Таблица аккордов Птолемея дает длины хорд окружности диаметром 120 в зависимости от числа градусовп в соответствующей дуге окружности, при п от 1/2 до 180 с шагом 1/2.[16] Тринадцать книг Альмагест являются наиболее влиятельными и значительными тригонометрическими работами всей древности.[17] Теорема, которая была центральной в вычислении хорд Птолемеем, была тем, что до сих пор известно как Теорема Птолемея, что сумма произведений противоположных сторон циклический четырехугольник равна произведению диагоналей. Частный случай теоремы Птолемея появился как предложение 93 в Евклиде. Данные. Теорема Птолемея приводит к эквиваленту четырех формул суммы и разности для синуса и косинуса, которые сегодня известны как формулы Птолемея, хотя сам Птолемей использовал аккорды вместо синуса и косинуса.[17] Далее Птолемей вывел эквивалент формулы полуугла
Птолемей использовал эти результаты для создания своих тригонометрических таблиц, но невозможно определить, были ли эти таблицы получены из работы Гиппарха.[17]
Ни таблицы Гиппарха, ни таблицы Птолемея не сохранились до наших дней, хотя описания других древних авторов не оставляют сомнений в том, что они когда-то существовали.[18]
Пифагор открыл многие свойства того, что впоследствии стало тригонометрическими функциями. В Теорема Пифагора, п2 + b2 = h2 является представлением основного тригонометрического тождества sin2(x) + cos2(x) = 1. Длина 1 - это гипотенуза любого прямоугольного треугольника и имеет длину катетов sin (x) и cos (x), где x является одним из двух непрямых углов. С учетом этого тождество, на котором основана тригонометрия, оказывается теоремой Пифагора.
Индийская математика
Некоторые из первых и очень важных достижений тригонометрии были в Индия. Влиятельные произведения 4–5 веков, известные как Сиддханты (их было пять, самый важный из которых Сурья Сиддханта[19]) сначала определил синус как современное соотношение между половиной угла и половиной хорды, а также определил косинус, Версина, и обратный синус.[20] Вскоре после этого другой Индийский математик и астроном, Арьябхата (476–550 гг. Н.э.), собранный и расширенный по развитию Сиддхант в важной работе, названной Арьябхатия.[21] В Сиддханты и Арьябхатия содержат самые ранние из сохранившихся таблиц значений синуса и Версина (1 - косинус) значения с интервалом 3,75 ° от 0 ° до 90 ° с точностью до 4 знаков после запятой.[22] Они использовали слова Джя для синуса, Коджа для косинуса, уткрама-джйа для версина, и Otkram jya для обратного синуса. Слова Джя и Коджа в конце концов стал синус и косинус соответственно после неправильного перевода, описанного выше.
В 7 веке Бхаскара I произвел формула для вычисления синуса острого угла без использования таблицы. Он также дал следующую приближенную формулу для греха (Икс) с относительной погрешностью менее 1,9%:
Позже, в 7 веке, Брахмагупта переработал формулу
(также получено ранее, как упоминалось выше) и Формула интерполяции Брахмагупты для вычисления значений синуса.[10]
Другой более поздний индийский автор тригонометрии был Бхаскара II в 12 веке. Бхаскара II развитый сферическая тригонометрия, и обнаружил множество тригонометрических результатов.
Бхаскара II был одним из первых, кто открыл и тригонометрические результаты, такие как:
Мадхава (ок. 1400 г.) сделал первые шаги в анализ тригонометрических функций и их бесконечная серия расширения. Он разработал концепции степенной ряд и Серия Тейлор, и произвел степенной ряд разложения синуса, косинуса, тангенса и арктангенса.[23][24] Используя приближения синуса и косинуса ряда Тейлора, он составил таблицу синусов с точностью до 12 знаков после запятой и таблицу косинусов с точностью до 9 знаков после запятой. Он также дал степенной ряд π и угол, радиус, диаметр, и длина окружности круга в терминах тригонометрических функций. Его работы были расширены его последователями в Керала школа до 16 века.[23][24]
| Нет. | Серии | Имя | Западные первооткрыватели сериала и приблизительные даты открытия[25] |
|---|---|---|---|
| 1 | грех Икс = Икс − Икс3 / 3! + Икс5 / 5! − Икс7 / 7! + ... | Синус серии Мадхавы | Исаак Ньютон (1670) и Вильгельм Лейбниц (1676) |
| 2 | потому что Икс = 1 − Икс2 / 2! + Икс4 / 4! − Икс6 / 6! + ... | Косинусный ряд Мадхавы | Исаак Ньютон (1670) и Вильгельм Лейбниц (1676) |
| 3 | загар−1Икс = Икс − Икс3 / 3 + Икс5 / 5 − Икс7 / 7 + ... | Арктангенсный ряд Мадхавы | Джеймс Грегори (1671) и Вильгельм Лейбниц (1676) |
Индийский текст Юктибхана содержит доказательство расширения синус и косинус функции, а также вывод и доказательство степенной ряд за обратная тангенс, обнаруженный Мадхавой. Юктибхана также содержит правила нахождения синусов и косинусов суммы и разности двух углов.
Китайская математика

В Китай, Арьябхата таблица синусов были переведены в Китайский математический книга Кайюань Чжаньцзин, составленный в 718 г. династия Тан.[26] Хотя китайцы преуспели в других областях математики, например в твердой геометрии, биномиальная теорема, и сложные алгебраические формулы, ранние формы тригонометрии не получили такого широкого признания, как в более раннем греческом, эллинистическом, индийском и исламском мирах.[27] Вместо этого ранние китайцы использовали эмпирический заменитель, известный как Чонг Ча, в то время как практическое использование плоской тригонометрии при использовании синуса, тангенса и секанса было известно.[26] Однако это зародышевое состояние тригонометрии в Китае начало медленно меняться и развиваться в течение Династия Сун (960–1279), где китайские математики начали уделять больше внимания необходимости сферической тригонометрии в календарной науке и астрономических расчетах.[26] В эрудит Китайский ученый, математик и чиновник Шен Куо (1031–1095) использовали тригонометрические функции для решения математических задач хорд и дуг.[26] Виктор Дж. Кац пишет, что в формуле Шена «техника пересечения окружностей» он создал приближение дуги.s круга с учетом диаметраd, сагитта v, и длинаc хорды, соединяющей дугу, длина которой он аппроксимировал как[28]
Сал Рестиво пишет, что работа Шена о длинах дуг окружностей послужила основой для сферическая тригонометрия разработан в 13 веке математиком и астрономом Го Шоуцзин (1231–1316).[29] Как утверждают историки Л. Гоше и Джозеф Нидхэм, Го Шоуцзин использовал сферическая тригонометрия в своих расчетах по улучшению календарная система и Китайская астрономия.[26][30] Наряду с более поздней иллюстрацией математических доказательств Го на китайском языке 17-го века Нидхэм утверждает, что:
Го использовал четырехугольную сферическую пирамиду, базальный четырехугольник которой состоял из одной экваториальной и одной эклиптической дуги вместе с двумя. дуги меридианов, один из которых прошел через летнее солнцестояние точка ... С помощью таких методов он смог получить du lü (степени экватора, соответствующие степеням эклиптики), ji cha (значения хорд для данных дуг эклиптики) и cha lü (разность между хордами дуг, различающихся на 1 степень).[31]
Несмотря на достижения Шэнь и Го в тригонометрии, еще одна существенная работа по китайской тригонометрии не будет опубликована снова до 1607 года, с двойной публикацией Элементы Евклида китайским чиновником и астрономом Сюй Гуанци (1562–1633) и итальянский иезуит Маттео Риччи (1552–1610).[32]
Средневековый исламский мир

Предыдущие работы были позже переведены и дополнены в средневековый исламский мир к Мусульманские математики в основном Персидский и Арабское происхождение, который сформулировал большое количество теорем, которые освободили предмет тригонометрии от зависимости от полной четырехугольник, как это было в эллинистической математике из-за применения Теорема Менелая. По словам Э. С. Кеннеди, именно после этого развития в исламской математике «появилась первая настоящая тригонометрия в том смысле, что только тогда объектом исследования стала сферический или самолет треугольник, его стороны и углы."[33]
Были также известны методы работы со сферическими треугольниками, в частности метод Менелай Александрийский, который разработал «теорему Менелая» для решения сферических задач.[11][34] Однако Кеннеди указывает, что, хотя в доисламской математике было возможно вычислить величины сферической фигуры, в принципе, с помощью таблицы хорд и теоремы Менелая, применение этой теоремы к сферическим задачам было очень сложно на практике.[35] Для соблюдения святых дней на Исламский календарь в котором тайминги были определены фазы Луны, астрономы первоначально использовали метод Менелая для расчета места Луна и звезды, хотя этот способ оказался неуклюжим и сложным. Это включало создание двух пересекающихся прямоугольные треугольники; Применяя теорему Менелая, можно было решить одну из шести сторон, но только если были известны другие пять сторон. Чтобы отличить время от солнце с высота, например, требовалось многократное применение теоремы Менелая. Для средневековья Исламские астрономы, была очевидная проблема - найти более простой тригонометрический метод.[36]
В начале 9 века нашей эры Мухаммад ибн Муса аль-Хваризми составили точные таблицы синусов и косинусов, а также первую таблицу касательных. Он также был пионером в сферическая тригонометрия. В 830 году нашей эры Хабаш аль-Хасиб аль-Марвази составили первую таблицу котангенсов.[37][38] Мухаммад ибн Джабир аль-Харрани аль-Баттани (Альбатениус) (853–929 гг. Н.э.) открыл взаимные функции секанса и косеканса и составил первую таблицу косекансов для каждой степени от 1 ° до 90 °.[38]
К 10 веку нашей эры в работах Абу аль-Вафа аль-Бузджани, Мусульманские математики использовали все шесть тригонометрические функции.[39] Абу аль-Вафа имел таблицы синусов с шагом 0,25 °, с точностью до 8 десятичных знаков и точные таблицы значений тангенса.[39] Он также разработал следующую тригонометрическую формулу:[40]
- (частный случай формулы Птолемея для сложения углов; см. выше)
В своем первоначальном тексте Абу аль-Вафа 'утверждает: «Если мы хотим этого, мы умножаем данный синус на косинус. минут, и результат - половина синуса двойного ".[40] Абу аль-Вафа также установил тождества сложения углов и разности, представленные с полными доказательствами:[40]
Для второго в тексте говорится: «Мы умножаем синус каждой из двух дуг на косинус другой. минут. Если нам нужен синус суммы, мы складываем произведения, если нам нужен синус разницы, мы берем их разницу ".[40]
Он также обнаружил закон синуса для сферической тригонометрии:[37]
Также в конце 10 - начале 11 веков нашей эры египетский астроном Ибн Юнус выполнил множество тщательных тригонометрических вычислений и продемонстрировал следующее тригонометрическая идентичность:[41]
Аль-Джайяни (989–1079) из аль-Андалус написал Книга неизвестных дуг сферы, который считается "первым трактатом о сферическая тригонометрия ".[42] Он "содержит формулы для правые треугольники, общий закон синусов и решение сферический треугольник с помощью полярного треугольника ». Этот трактат позже оказал« сильное влияние на европейскую математику », и его« определение соотношения как числа "и" метод решения сферического треугольника, когда все стороны неизвестны ", вероятно, повлияли Региомонтан.[42]
Методика триангуляция был впервые разработан мусульманскими математиками, которые применили его на практике, например геодезия[43] и Исламская география, как описано Абу Райхан Бируни в начале 11 века. Сам Бируни познакомил с техникой триангуляции измерить размер Земли и расстояния между разными местами.[44] В конце 11 века Омар Хайям (1048–1131) решено кубические уравнения с использованием приближенных численных решений, найденных путем интерполяции в тригонометрических таблицах. В 13 веке Насир ад-Дин ат-Туси был первым, кто стал рассматривать тригонометрию как математическую дисциплину, независимую от астрономии, и развил сферическую тригонометрию в ее нынешней форме.[38] Он перечислил шесть различных случаев прямоугольного треугольника в сферической тригонометрии, а в своей На секторном рисунке, он сформулировал закон синусов для плоских и сферических треугольников, открыл закон касательных для сферических треугольников и предоставил доказательства обоих этих законов.[45] Насир ад-Дин ат-Туси был описан как создатель тригонометрии как самостоятельной математической дисциплины.[46][47][48]
В 15 веке Джамшид аль-Каши предоставил первое явное утверждение закон косинусов в форме, подходящей для триангуляция.[нужна цитата ] В Франция, закон косинусов по-прежнему называется Теорема Аль-Каши. Он также дал тригонометрические таблицы значений синусоидальной функции четырем шестидесятеричный цифры (эквивалентные 8 десятичным разрядам) для каждого 1 ° аргумента с добавлением разностей для каждой 1/60 от 1 °.[нужна цитата ] Улугбека также дает точные таблицы синусов и тангенсов с точностью до 8 десятичных знаков примерно в одно и то же время.[нужна цитата ]
Европейский ренессанс и впоследствии
В 1342 году Леви бен Гершон, известный как Герсонид, написал О синусах, аккордах и дугах, в частности доказывая синус закон для плоских треугольников и придания пятизначности таблицы синусов.[49]
Упрощенная тригонометрическая таблица "Toleta de Marteloio ", использовался моряками в Средиземное море в XIV-XV вв. для расчета навигация курсы. Это описывается Рамон Лулль из Майорка в 1295 г. и изложен в атласе 1436 г. Венецианский капитан Андреа Бьянко.
Региомонтан был, возможно, первым математиком в Европе, который рассматривал тригонометрию как отдельную математическую дисциплину,[50] в его De triangulis omnimodis написан в 1464 году, а также его более поздние Tabulae directionum которая включала безымянную функцию касательной. Opus palatinum de triangulis из Георг Иоахим Ретикус, студент Коперник, вероятно, был первым в Европе, кто определил тригонометрические функции непосредственно в терминах прямоугольных треугольников, а не окружностей, с таблицами для всех шести тригонометрических функций; эта работа была закончена учеником Ретикуса Валентин Ото в 1596 г.
В 17 веке Исаак Ньютон и Джеймс Стирлинг разработал общую интерполяционную формулу Ньютона – Стирлинга для тригонометрических функций.
В 18 веке Леонард Эйлер с Введение в анализин бесконечный (1748) был в основном ответственен за установление аналитического подхода к тригонометрическим функциям в Европе, вывод их бесконечных рядов и представление "Формула Эйлера " еix = cosИкс + я грехИкс. Эйлер использовал почти современные сокращения грех., cos., запах, детская кроватка., сек., и cosec. Перед этим, Роджер Котс вычислил производную синуса в своем Harmonia Mensurarum (1722).[51]Также в 18 веке Брук Тейлор определил общий ряд Тейлора и дал разложения ряда и приближения для всех шести тригонометрических функций. Работы Джеймс Грегори в 17 веке и Колин Маклорен в 18 веке также оказали большое влияние на развитие тригонометрических рядов.
Смотрите также
- Греческая математика
- История математики
- Тригонометрические функции
- Тригонометрия
- Таблица аккордов Птолемея
- Таблица синусов Арьябхаты
- Рациональная тригонометрия
Цитаты и сноски
- ^ Отто Нойгебауэр (1975). История древней математической астрономии. 1. Springer-Verlag. п. 744. ISBN 978-3-540-06995-9.
- ^ Кац 1998, п. 212.
- ^ «тригонометрия». Интернет-словарь этимологии.
- ^ Джамбхекар, Ашок (январь 1983 г.). «Индийские книги квартала». India Quarterly: журнал международных отношений. 39 (1): 106–108. Дои:10.1177/097492848303900122. ISSN 0974-9284.
- ^ а б Бойер 1991, п. 252: Это был перевод Роберта Честерского с арабского, в результате которого появилось слово «синус». В тригонометрии индусы дали полуаккорду имя джива, а арабы приняли это название как джиба. В арабском языке есть также слово jaib, означающее «залив» или «залив». Когда Роберт Честерский пришел переводить техническое слово jiba, он, кажется, перепутал его со словом jaib (возможно, потому, что гласные были опущены); поэтому он использовал слово «синус», латинское слово, означающее «залив» или «вход».
- ^ а б c d е ж Маор, Эли (1998). Тригонометрические наслаждения. Princeton University Press. п.20. ISBN 978-0-691-09541-7.
- ^ а б О'Коннор, Дж. Дж .; Робертсон, Э. Ф. (1996). «Тригонометрические функции». Архив истории математики MacTutor.
- ^ а б c Бойер, Карл Бенджамин (1991). «Греческая тригонометрия и измерение». История математики. Джон Вили и сыновья. стр.166 –167.
Следует напомнить, что со времен Гиппарха и до наших дней не существовало таких вещей, как тригонометрия. соотношения. Греки, а после них индусы и арабы использовали тригонометрические линии. Сначала они принимали форму, как мы видели, аккордов в круге, и Птолемей стал обязан связывать числовые значения (или приближения) с аккордами. [...] Не исключено, что мера в 260 градусов была перенесена из астрономии, где зодиак был разделен на двенадцать «знаков» или 36 «деканов». Цикл времен года, составляющий примерно 360 дней, легко можно было бы привести в соответствие системе зодиакальных знаков и деканов, разделив каждый знак на тридцать частей и каждый декан на десять частей. Наша общая система измерения углов может вытекать из этого соответствия. Более того, поскольку вавилонская позиционная система для дробей настолько явно превосходила египетскую единичную дробь и греческую обыкновенную дробь, для Птолемея было естественным разделить свои градусы на шестьдесят partes minutae primae, каждый из них на шестьдесят partes minutae secundae, и так далее. Наши слова «минута» и «секунда» произошли от латинских фраз, которые переводчики использовали в этой связи. Несомненно, именно шестидесятеричная система привела к тому, что Птолемей разделил диаметр своего тригонометрического круга на 120 частей; каждую из них он далее разделил на шестьдесят минут и каждую минуту продолжительностью шестьдесят секунд.
- ^ а б c Бойер, Карл Бенджамин (1991). «Греческая тригонометрия и измерение». История математики. Джон Вили и сыновья. стр.158 –159.
Тригонометрия, как и другие разделы математики, не была делом одного человека или нации. Теоремы об отношении сторон подобных треугольников были известны и использовались древними египтянами и вавилонянами. Ввиду отсутствия в доэллинской эпохе концепции угловой меры такое исследование лучше было бы назвать «трилатерометрией» или мерой трехсторонних многоугольников (трехугольников), чем «тригонометрией», мерой частей треугольника. У греков мы сначала находим систематическое изучение отношений между углами (или дугами) в окружности и длинами хорд, соединяющих их. Свойства хорд, как меры центрального и вписанного в окружности углов, были знакомы грекам времен Гиппократа, и вполне вероятно, что Евдокс использовал соотношения и угловые меры для определения размера Земли и относительных расстояний до Солнца. и луна. В работах Евклида нет тригонометрии в строгом смысле этого слова, но есть теоремы, эквивалентные конкретным тригонометрическим законам или формулам. Предложения II.12 и 13 Элементы, например, законы косинусов для тупых и острых углов соответственно, сформулированные на геометрическом, а не тригонометрическом языке и доказанные методом, аналогичным тому, который использовал Евклид в связи с теоремой Пифагора. Теоремы о длинах хорд по сути являются приложениями современного закона синусов. Мы видели, что теорему Архимеда о разорванной хорде легко перевести на тригонометрический язык, аналогично формулам для синусов сумм и разностей углов.
- ^ а б Джозеф 2000 С. 383–384.
- ^ а б c d е ж Бойер, Карл Бенджамин (1991). «Греческая тригонометрия и измерение». История математики. Джон Вили и сыновья. п.163.
В Книге I этого трактата Менелай устанавливает основу для сферических треугольников, аналогичную той, что у Евклида I для плоских треугольников. Включена теорема без евклидова аналога - что два сферических треугольника равны, если соответствующие углы равны (Менелай не различал конгруэнтные и симметричные сферические треугольники); и теорема А + B + C > 180 ° устанавливается. Вторая книга Sphaerica описывает применение сферической геометрии к астрономическим явлениям и представляет небольшой математический интерес. Книга III, последняя, содержит хорошо известную «теорему Менелая» как часть того, что по сути является сферической тригонометрией в типичной греческой форме - геометрии или тригонометрии хорд в окружности. В кружке на рис. 10.4 мы должны написать, что хорда AB в два раза больше синуса половины центрального угла AOB (умноженного на радиус окружности). Менелай и его греческие последователи вместо этого называли AB просто хордой, соответствующей дуге AB. Если BOB '- это диаметр окружности, то хорда A' равна удвоенному косинусу половины угла AOB (умноженному на радиус окружности).
- ^ а б Бойер, Карл Бенджамин (1991). «Греческая тригонометрия и измерение». История математики. Джон Вили и сыновья. п.159.
Вместо этого у нас есть трактат, возможно, составленный ранее (около 260 г. до н.э.), О размерах и расстояниях Солнца и Луны, что предполагает геоцентрическую вселенную. В этой работе Аристарх заметил, что, когда Луна только наполовину полная, угол между линиями взгляда на Солнце и Луну меньше прямого угла на одну тридцатую квадранта. (Систематическое введение круга в 360 ° произошло немного позже. На современном тригонометрическом языке это означало бы, что отношение расстояния от Луны к расстоянию до Солнца (отношение ME к SE на рис. 10.1) есть грех ( 3 °). Тригонометрические таблицы еще не были разработаны, Аристарх прибег к известной геометрической теореме того времени, которая теперь будет выражена в неравенство sin α / sin β <α / β
- ^ а б Бойер, Карл Бенджамин (1991). «Греческая тригонометрия и измерение». История математики. Джон Вили и сыновья. п.162.
В течение примерно двух с половиной веков, от Гиппократа до Эратосфена, греческие математики изучали взаимосвязи между линиями и кругами и применяли их в различных астрономических задачах, но систематической тригонометрии не последовало. Затем, предположительно во второй половине II века до нашей эры, первая тригонометрическая таблица была составлена астрономом Гиппархом из Никеи (ок. 180 - ок. 125 г. до н.э.), который, таким образом, получил право называться «отцом тригонометрия ». Аристарх знал, что в данном круге отношение дуги к хорде уменьшается по мере уменьшения дуги от 180 ° до 0 °, стремясь к пределу 1. Однако, похоже, что только после того, как Гиппарх предпринял эту задачу, кто-либо табулировал соответствующие значения дуга и хорда для целого ряда углов.
- ^ Бойер, Карл Бенджамин (1991). «Греческая тригонометрия и измерение». История математики. Джон Вили и сыновья. п.162.
Неизвестно, когда именно систематическое использование круга 360 ° вошло в математику, но, по-видимому, это во многом связано с Гиппархом в связи с его таблицей аккордов. Возможно, что он заменил Гипсикла, который ранее разделил день на части, что, возможно, было предложено вавилонской астрономией.
- ^ Нидхэм 1986, п. 108.
- ^ Тумер, Джеральд Дж. (1998). Альмагест Птолемея. Издательство Принстонского университета. ISBN 978-0-691-00260-6.
- ^ а б c d Бойер, Карл Бенджамин (1991). «Греческая тригонометрия и измерение». История математики. Джон Вили и сыновья. стр.164 –166.
Теорема Менелая сыграла фундаментальную роль в сферической тригонометрии и астрономии, но, безусловно, самая влиятельная и значимая тригонометрическая работа всей древности была написана Птолемеем Александрийским примерно через полвека после Менелая. [...] О жизни автора мы так же мало осведомлены, как и о жизни автора Элементов. Мы не знаем, когда и где родились Евклид и Птолемей. Мы знаем, что Птолемей проводил наблюдения в Александрии от нашей эры. 127–151 и, следовательно, предполагаем, что он родился в конце I века. Суид, писатель X века, сообщил, что Птолемей был жив при Марке Аврелии (император с 161 по 180 год нашей эры).
Птолемея Альмагест предполагается, что своими методами он в значительной степени обязан Аккорды по кругу Гиппарха, но размер задолженности не может быть достоверно оценен. Ясно, что в астрономии Птолемей использовал каталог положений звезд, завещанный Гиппархом, но невозможно определить, были ли тригонометрические таблицы Птолемея в значительной степени заимствованы из его выдающегося предшественника. [...] Центральным в вычислении хорд Птолемея было геометрическое утверждение, все еще известное как «теорема Птолемея»: [...] то есть сумма произведений противоположных сторон вписанного четырехугольника равна произведению диагоналей. [...] Частный случай теоремы Птолемея появился у Евклида. Данные (Предложение 93): [...] Теорема Птолемея, следовательно, приводит к результату sin (α − β) = грехα потому чтоβ - cosα грехΒ. Подобные рассуждения приводят к формуле [...] Эти четыре формулы суммы и разности, следовательно, часто известны сегодня как формулы Птолемея.
Это была формула для синуса разности, или, точнее, хорды разности, которую Птолемей нашел особенно полезной при построении своих таблиц. Другая формула, которая ему очень пригодилась, была эквивалентом нашей формулы полуугла. - ^ Бойер 1991 С. 158–168.
- ^ Бойер 1991, п. 208.
- ^ Бойер 1991, п. 209.
- ^ Бойер 1991, п. 210.
- ^ Бойер 1991, п. 215.
- ^ а б О'Коннор, Дж. Дж .; Робертсон, Э. Ф. (2000). «Мадхава Сангамаграммы». Архив истории математики MacTutor.
- ^ а б Пирс, Ян Г. (2002). «Мадхава Сангамаграммы». Архив истории математики MacTutor.
- ^ Чарльз Генри Эдвардс (1994). Историческое развитие математического анализа. Springer Study Edition Series (3-е изд.). Springer. п. 205. ISBN 978-0-387-94313-8.
- ^ а б c d е Нидхэм 1986, п. 109.
- ^ Нидхэм 1986 С. 108–109.
- ^ Кац 2007, п. 308.
- ^ Restivo 1992, п. 32.
- ^ Гоше 1917, п. 151.
- ^ Нидхэм 1986 С. 109–110.
- ^ Нидхэм 1986, п. 110.
- ^ Кеннеди, Э. С. (1969). «История тригонометрии». 31-й ежегодник. Вашингтон, округ Колумбия: Национальный совет учителей математики. (ср. Хак, Сайед Номанул (1996). «Индийский и персидский фон». В Сейед Хоссейн Наср; Оливер Лиман (ред.). История исламской философии. Рутледж. С. 52–70 [60–63]. ISBN 978-0-415-13159-9.)
- ^ О'Коннор, Джон Дж.; Робертсон, Эдмунд Ф., «Менелай Александрийский», Архив истории математики MacTutor, Сент-Эндрюсский университет. «Книга 3 посвящена сферической тригонометрии и включает теорему Менелая».
- ^ Кеннеди, Э. С. (1969). «История тригонометрии». 31-й ежегодник. Вашингтон, округ Колумбия: Национальный совет учителей математики: 337. (ср. Хак, Сайед Номанул (1996). «Индийский и персидский фон». В Сейед Хоссейн Наср; Оливер Лиман (ред.). История исламской философии. Рутледж. С. 52–70 [68]. ISBN 978-0-415-13159-9.)
- ^ Джинджерич, Оуэн (апрель 1986). «Исламская астрономия». Scientific American. 254 (10): 74. Bibcode:1986SciAm.254d..74G. Дои:10.1038 / scientificamerican0486-74. Архивировано из оригинал на 2011-01-01. Получено 2008-05-18.
- ^ а б Жак Сезиано, "Исламская математика", стр. 157, дюйм Селин, Хелайн; Д'Амброзио, Убиратан, ред. (2000). Математика в разных культурах: история незападной математики. Springer Science + Business Media. ISBN 978-1-4020-0260-1.
- ^ а б c «тригонометрия». Британская энциклопедия. Получено 2008-07-21.
- ^ а б Бойер 1991, п. 238.
- ^ а б c d Мусса, Али (2011). «Математические методы в Альмагесте Абу аль-Вафаха и определения Киблы». Арабские науки и философия. Издательство Кембриджского университета. 21 (1): 1–56. Дои:10.1017 / S095742391000007X.
- ^ Уильям Чарльз Брайс,Исторический атлас ислама ', стр.413
- ^ а б О'Коннор, Джон Дж.; Робертсон, Эдмунд Ф., «Абу Абдаллах Мухаммад ибн Муад Аль-Джайяни», Архив истории математики MacTutor, Сент-Эндрюсский университет.
- ^ Дональд Рутледж Хилл (1996), «Инжиниринг», в Рошди Рашед, Энциклопедия истории арабской науки, Vol. 3, стр. 751–795 [769].
- ^ О'Коннор, Джон Дж.; Робертсон, Эдмунд Ф., «Абу Аррайхан Мухаммад ибн Ахмад аль-Бируни», Архив истории математики MacTutor, Сент-Эндрюсский университет.
- ^ Берггрен, Дж. Леннарт (2007). «Математика в средневековом исламе». Математика Египта, Месопотамии, Китая, Индии и ислама: Справочник. Издательство Принстонского университета. п. 518. ISBN 978-0-691-11485-9.
- ^ "Биография Ат-Туси_насир". www-history.mcs.st-andrews.ac.uk. Получено 2018-08-05.
Одним из наиболее важных вкладов ат-Туси в математику было создание тригонометрии как самостоятельной математической дисциплины, а не просто инструмента для астрономических приложений. В «Трактате о четырехугольнике» ат-Туси впервые изложил всю систему плоской и сферической тригонометрии. Эта работа действительно первая в истории по тригонометрии как независимому разделу чистой математики и первая, в которой изложены все шесть случаев для прямоугольного сферического треугольника.
- ^ Берггрен, Дж. Л. (октябрь 2013 г.). «Исламская математика». Кембриджская история науки. Издательство Кембриджского университета. С. 62–83. Дои:10.1017 / CHO9780511974007.004. ISBN 978-0-511-97400-7.
- ^ electricpulp.com. "USI, NAṢIR-AL-DIN i. Биография - Encyclopaedia Iranica". www.iranicaonline.org. Получено 2018-08-05.
Его главный вклад в математику (Nasr, 1996, стр. 208-214), как говорят, был в тригонометрии, которая впервые была составлена им как самостоятельная дисциплина. Сферическая тригонометрия также обязана своим развитием его усилиям, и это включает в себя концепцию шести фундаментальных формул для решения сферических прямоугольных треугольников.
- ^ Чарльз Г. Симонсон (зима 2000 г.). "Математика Леви бен Гершона, Ральбага" (PDF). Бекхол Дерахеха Даеху. Издательство Университета Бар-Илан. 10: 5–21.
- ^ Бойер 1991, п. 274.
- ^ Кац, Виктор Дж. (Ноябрь 1987 г.). «Исчисление тригонометрических функций». Historia Mathematica. 14 (4): 311–324. Дои:10.1016/0315-0860(87)90064-4.. Доказательство Котеса упоминается на стр. 315.
Рекомендации
- Бойер, Карл Бенджамин (1991). История математики (2-е изд.). John Wiley & Sons, Inc. ISBN 978-0-471-54397-8.
- Гоше, Л. (1917). Note Sur La Trigonométrie Sphérique de Kouo Cheou-King.
- Джозеф, Джордж Г. (2000). Гребень павлина: неевропейские корни математики (2-е изд.). Лондон: Книги о пингвинах. ISBN 978-0-691-00659-8.
- Кац, Виктор Дж. (1998). История математики / Введение (2-е изд.). Эддисон Уэсли. ISBN 978-0-321-01618-8.
- Кац, Виктор Дж. (2007). Математика Египта, Месопотамии, Китая, Индии и ислама: Справочник. Принстон: Издательство Принстонского университета. ISBN 978-0-691-11485-9.
- Нидхэм, Джозеф (1986). Наука и цивилизация в Китае: Том 3, Математика и науки о небе и Земле. Тайбэй: Caves Books, Ltd.
- Рестиво, Сал (1992). Математика в обществе и истории: социологические исследования. Дордрехт: Kluwer Academic Publishers. ISBN 1-4020-0039-1.