Шестиугольная черепичная сотовая конструкция - Hexagonal tiling honeycomb

Шестиугольная черепичная сотовая конструкция
Перспективная проекция Посмотреть в пределах Модель диска Пуанкаре
Тип	Гиперболические обычные соты Паракомпактные однородные соты
Символы Шлефли	{6,3,3} т {3,6,3} 2т {6,3,6} 2т {6,3^[3]} т {3^[3,3]}
Диаграммы Кокстера	↔ ↔ ↔ ↔
Клетки	{6,3}
Лица	шестиугольник {6}
Край фигура	треугольник {3}
Фигура вершины	тетраэдр {3,3}
Двойной	Сотовый четырехгранник Order-6
Группы Кокстера	${\displaystyle {\overline {V}}_{3}}$, [3,3,6] ${\displaystyle {\overline {Y}}_{3}}$, [3,6,3] ${\displaystyle {\overline {Z}}_{3}}$, [6,3,6] ${\displaystyle {\overline {VP}}_{3}}$, [6,3^[3]] ${\displaystyle {\overline {PP}}_{3}}$, [3^[3,3]]
Свойства	Обычный

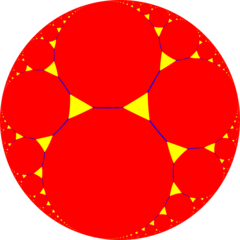
В области гиперболическая геометрия, то шестиугольная черепичная сотовая конструкция один из 11 обычные паракомпактные соты в 3-х мерном гиперболическое пространство. это паракомпакт поскольку она имеет клетки состоит из бесконечного числа лиц. Каждая ячейка - это шестиугольная черепица вершины которого лежат на горосфера, поверхность в гиперболическом пространстве, которая приближается к идеальная точка на бесконечности.

В Символ Шлефли шестиугольной черепичной сотовой конструкции составляет {6,3,3}. Так как шестиугольная черепица равно {6,3}, у этой соты есть три таких шестиугольных мозаики, пересекающихся на каждом краю. Поскольку символ Шлефли тетраэдр равно {3,3}, вершина фигуры этой соты - тетраэдр. Таким образом, четыре шестиугольных мозаики пересекаются в каждой вершине этой соты, шесть шестиугольников пересекаются в каждой вершине и четыре ребра пересекаются в каждой вершине.^[1]

Картинки

В перспективе за пределами Модель диска Пуанкаре, на изображении выше показан один шестиугольная черепица ячейка внутри соты и ее средний радиус горосфера (горосфера, инцидентная с серединами краев). В этой проекции шестиугольники бесконечно малы по направлению к бесконечной границе, асимптотический к единой идеальной точке. Его можно рассматривать как похожий на апейрогональная мозаика порядка 3, {∞, 3} из H², с участием орициклы описывающие вершины апейрогональный лица.

{6,3,3}	{∞,3}
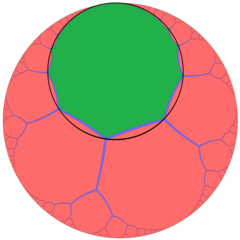Одна шестиугольная мозаичная ячейка шестиугольной мозаичной сотовой структуры	An апейрогональная мозаика порядка 3 с зеленым апейрогоном и его орициклом

Построения симметрии

Отношения подгруппы

Он имеет в общей сложности пять отражающих конструкций из пяти связанных групп Кокстера, все с четырьмя зеркалами, и только первое из них является обычным: [6,3,3], [3,6,3], [6,3,6], [6,3^[3]] и [3^[3,3]] , имея 1, 4, 6, 12 и 24 раза более крупные фундаментальные области соответственно. В Обозначение Кокстера разметки подгрупп, они связаны как: [6, (3,3)^*] (удалить 3 зеркала, подгруппа индекса 24); [3,6,3^*] или [3^*, 6,3] (удалить 2 зеркала, подгруппа индекса 6); [1⁺,6,3,6,1⁺] (удалить два ортогональных зеркала, подгруппа индекса 4); все они изоморфны [3^[3,3]]. Окруженные диаграммы Кокстера: , , , и , представляющих различные типы (цвета) шестиугольных мозаик в Строительство Wythoff.

Связанные многогранники и соты

Соты шестиугольной черепицы - это обычные гиперболические соты в 3-м пространстве и один из 11 паракомпактных.

11 паракомпактных обычных сот
{6,3,3}	{6,3,4}	{6,3,5}	{6,3,6}	{4,4,3}	{4,4,4}
{3,3,6}	{4,3,6}	{5,3,6}	{3,6,3}	{3,4,4}

это одна из 15 однородных паракомпактных сот в группе Кокстера [6,3,3] вместе с двойственной ей группой четырехгранные соты порядка 6.

[6,3,3] семейные соты
{6,3,3}	г {6,3,3}	т {6,3,3}	рр {6,3,3}	т0,3{6,3,3}	tr {6,3,3}	т0,1,3{6,3,3}	т0,1,2,3{6,3,3}
{3,3,6}	г {3,3,6}	т {3,3,6}	рр {3,3,6}	2т {3,3,6}	tr {3,3,6}	т0,1,3{3,3,6}	т0,1,2,3{3,3,6}

Это часть последовательности регулярная полихора, которые включают 5-элементный {3,3,3}, тессеракт {4,3,3} и 120 ячеек {5,3,3} евклидова 4-мерного пространства вместе с другими гиперболическими сотами, содержащими четырехгранный фигуры вершин.

{п, 3,3} соты
Космос		S^3			ЧАС^3
Форма		Конечный			Паракомпакт	Некомпактный
имя		{3,3,3}	{4,3,3}	{5,3,3}	{6,3,3}	{7,3,3}	{8,3,3}	... {∞,3,3}
Образ
Диаграммы Кокстера	1
	4
	6
	12
	24
Клетки {p, 3}		{3,3}	{4,3}	{5,3}	{6,3}	{7,3}	{8,3}	{∞,3}

Он также является частью последовательности регулярных сот формы {6,3, p}, каждая из которых состоит из шестиугольная черепица клетки:

{6,3, п} соты [ v т е ]
Космос	ЧАС^3
Форма	Паракомпакт				Некомпактный
имя	{6,3,3}	{6,3,4}	{6,3,5}	{6,3,6}	{6,3,7}	{6,3,8}	... {6,3,∞}
Coxeter
Образ
Вершина фигура {3, п}	{3,3}	{3,4}	{3,5}	{3,6}	{3,7}	{3,8}	{3,∞}

Ректифицированная шестиугольная черепица сота

Ректифицированная шестиугольная черепица сота
Тип	Паракомпактные однородные соты
Символы Шлефли	r {6,3,3} или t1{6,3,3}
Диаграммы Кокстера	↔
Клетки	{3,3} г {6,3} или
Лица	треугольник {3} шестиугольник {6}
Фигура вершины	треугольная призма
Группы Кокстера	${\displaystyle {\overline {V}}_{3}}$, [3,3,6] ${\displaystyle {\overline {P}}_{3}}$, [3,3^[3]]
Свойства	Вершинно-транзитивный, реберный транзитивный

В выпрямленная шестиугольная черепичная сотовая структура, т₁{6,3,3}, имеет четырехгранный и трехгексагональная черепица грани, с треугольная призма вершина фигуры. В Конструкция полусимметрии чередует два типа тетраэдров.

Шестиугольная черепичная сотовая конструкция	Ректифицированная шестиугольная черепица сота или
Связанный H^2 мозаики
Апейрогональная мозаика порядка 3	Триапейрогональная черепица или

Усеченные шестиугольные черепичные соты

Усеченные шестиугольные черепичные соты
Тип	Паракомпактные однородные соты
Символ Шлефли	т {6,3,3} или т0,1{6,3,3}
Диаграмма Кокстера
Клетки	{3,3} т {6,3}
Лица	треугольник {3} двенадцатигранник {12}
Фигура вершины	треугольная пирамида
Группы Кокстера	${\displaystyle {\overline {V}}_{3}}$, [3,3,6]
Свойства	Вершинно-транзитивный

В усеченные шестиугольные черепичные соты, т_0,1{6,3,3}, имеет четырехгранный и усеченная шестиугольная мозаика грани, с треугольная пирамида вершина фигуры.

Он похож на двумерный гиперболический усеченная апейрогональная мозаика порядка 3, t {∞, 3} с апейрогональными и треугольными гранями:

Шестиугольные черепичные соты с усеченной бородкой

Шестиугольные черепичные соты с усеченной бородкой Тетраэдрические соты с усеченной структурой порядка 6
Тип	Паракомпактные однородные соты
Символ Шлефли	2т {6,3,3} или т1,2{6,3,3}
Диаграмма Кокстера	↔
Клетки	т {3,3} т {3,6}
Лица	треугольник {3} шестиугольник {6}
Фигура вершины	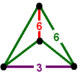дигональный дисфеноид
Группы Кокстера	${\displaystyle {\overline {V}}_{3}}$, [3,3,6] ${\displaystyle {\overline {P}}_{3}}$, [3,3^[3]]
Свойства	Вершинно-транзитивный

В усеченные шестиугольные черепичные соты или усеченная по битам тетраэдрическая сотовая структура порядка 6, т_1,2{6,3,3}, имеет усеченный тетраэдр и шестиугольная черепица ячейки, с дигональный дисфеноид вершина фигуры.

Гексагональные гексагональные черепичные соты

Гексагональные гексагональные черепичные соты
Тип	Паракомпактные однородные соты
Символ Шлефли	rr {6,3,3} или t0,2{6,3,3}
Диаграмма Кокстера
Клетки	г {3,3} рр {6,3} {}×{3}
Лица	треугольник {3} квадрат {4} шестиугольник {6}
Фигура вершины	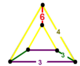клин
Группы Кокстера	${\displaystyle {\overline {V}}_{3}}$, [3,3,6]
Свойства	Вершинно-транзитивный

В скошенные шестиугольные черепичные соты, т_0,2{6,3,3}, имеет октаэдр, ромбитогексагональная черепица, и треугольная призма ячейки, с клин вершина фигуры.

Гексагональная черепица с усеченными сотовыми ячейками

Гексагональная черепица с усеченными сотовыми ячейками
Тип	Паракомпактные однородные соты
Символ Шлефли	tr {6,3,3} или t0,1,2{6,3,3}
Диаграмма Кокстера
Клетки	т {3,3} tr {6,3} {}×{3}
Лица	треугольник {3} квадрат {4} шестиугольник {6} двенадцатигранник {12}
Фигура вершины	зеркальная клиновидная кость
Группы Кокстера	${\displaystyle {\overline {V}}_{3}}$, [3,3,6]
Свойства	Вершинно-транзитивный

В усеченные шестиугольные черепичные соты, т_0,1,2{6,3,3}, имеет усеченный тетраэдр, усеченная трехгексагональная мозаика, и треугольная призма ячейки, с зеркальная клиновидная кость вершина фигуры.

Гексагональная гексагональная черепичная сотовая структура

Гексагональная гексагональная черепичная сотовая структура
Тип	Паракомпактные однородные соты
Символ Шлефли	т0,3{6,3,3}
Диаграмма Кокстера
Клетки	{3,3} {6,3} {}×{6} {}×{3}
Лица	треугольник {3} квадрат {4} шестиугольник {6}
Фигура вершины	нерегулярный треугольная антипризма
Группы Кокстера	${\displaystyle {\overline {V}}_{3}}$, [3,3,6]
Свойства	Вершинно-транзитивный

В многослойная шестиугольная черепица с сотовой структурой, т_0,3{6,3,3}, имеет тетраэдр, шестиугольная черепица, шестиугольная призма, и треугольная призма ячейки, с нерегулярным треугольная антипризма вершина фигуры.

Гексагональная черепичная усеченная сотовая структура

Гексагональная черепичная усеченная сотовая структура
Тип	Паракомпактные однородные соты
Символ Шлефли	т0,1,3{6,3,3}
Диаграмма Кокстера
Клетки	рр {3,3} {} x {3} {} x {12} т {6,3}
Лица	треугольник {3} квадрат {4} шестиугольник {6} двенадцатигранник {12}
Фигура вершины	равнобедренно-трапециевидный пирамида
Группы Кокстера	${\displaystyle {\overline {V}}_{3}}$, [3,3,6]
Свойства	Вершинно-транзитивный

В усеченные шестиугольные черепичные соты, т_0,1,3{6,3,3}, имеет кубооктаэдр, треугольная призма, двенадцатигранная призма, и усеченная шестиугольная мозаика ячейки, с равнобедренно-трапециевидный пирамида вершина фигуры.

Гексагональные гексагональные соты с круглыми краями

Гексагональные гексагональные соты с круглыми краями усеченные четырехгранные соты порядка 6
Тип	Паракомпактные однородные соты
Символ Шлефли	т0,2,3{6,3,3}
Диаграмма Кокстера
Клетки	т {3,3} {} x {6} рр {6,3}
Лица	треугольник {3} квадрат {4} шестиугольник {6}
Фигура вершины	равнобедренно-трапециевидный пирамида
Группы Кокстера	${\displaystyle {\overline {V}}_{3}}$, [3,3,6]
Свойства	Вершинно-транзитивный

В многослойные шестиугольные черепичные соты или усеченные четырехгранные соты порядка 6, т_0,2,3{6,3,3}, имеет усеченный тетраэдр, шестиугольная призма, и ромбитогексагональная черепица ячейки, с равнобедренно-трапециевидный пирамида вершина фигуры.

Многослойные шестиугольные черепичные соты

Многослойные шестиугольные черепичные соты Омнитусеченные четырехгранные соты порядка 6
Тип	Паракомпактные однородные соты
Символ Шлефли	т0,1,2,3{6,3,3}
Диаграмма Кокстера
Клетки	tr {3,3} {} x {6} {} x {12} tr {6,3}
Лица	квадрат {4} шестиугольник {6} двенадцатигранник {12}
Фигура вершины	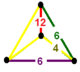нерегулярный тетраэдр
Группы Кокстера	${\displaystyle {\overline {V}}_{3}}$, [3,3,6]
Свойства	Вершинно-транзитивный

В многослойные шестиугольные черепичные соты или многослойные тетраэдрические соты порядка 6, т_0,1,2,3{6,3,3}, имеет усеченный октаэдр, шестиугольная призма, двенадцатигранная призма, и усеченная трехгексагональная мозаика ячейки, с нерегулярным тетраэдр вершина фигуры.

Смотрите также

• Выпуклые однородные соты в гиперболическом пространстве
• Регулярные мозаики гиперболического 3-мерного пространства
• Паракомпактные однородные соты
• Чередующиеся шестиугольные черепичные соты

использованная литература

1. Coxeter Красота геометрии, 1999, Глава 10, Таблица III

• Coxeter, Правильные многогранники, 3-й. изд., Dover Publications, 1973. ISBN  0-486-61480-8. (Таблицы I и II: Правильные многогранники и соты, стр. 294–296)
• Красота геометрии: двенадцать эссе (1999), Dover Publications, LCCN  99-35678, ISBN  0-486-40919-8 (Глава 10, Регулярные соты в гиперболическом пространстве ) Таблица III
• Джеффри Р. Уикс Форма космоса, 2-е издание ISBN  0-8247-0709-5 (Главы 16-17: Геометрии на трехмерных многообразиях I, II)
• Н. В. Джонсон, Р. Келлерхальс, Дж. Г. Рэтклифф, С. Т. Чанц, Размер гиперболического симплекса Кокстера, Transformation Groups (1999), Volume 4, Issue 4, pp 329–353. [1] [2]
• Н. В. Джонсон, Р. Келлерхальс, Дж. Г. Рэтклифф, С. Т. Чанц, Классы соизмеримости гиперболических групп Кокстера, (2002) H³: p130. [3]

внешние ссылки

• Джон Баэз, Визуальное понимание: {6,3,3} Соты (2014/03/15)
• Джон Баэз, Визуальное понимание: {6,3,3} Соты в верхнем полупространстве (2013/09/15)
• Джон Баэз, Визуальное понимание: Усеченные {6,3,3} соты (2016/12/01)