Заполненный набор Юля - Filled Julia set

В заполненный набор Юля ${\displaystyle \ K(f)}$ полинома ${\displaystyle \ f}$ является :

• а Юля набор и это интерьер,
• неэкранированный набор

Формальное определение

Заполненный Юля набор ${\displaystyle \ K(f)}$ полинома ${\displaystyle \ f}$ определяется как множество всех точек ${\displaystyle z\,}$ динамической плоскости, которые имеют ограниченный орбита относительно ${\displaystyle \ f}$

${\displaystyle \ K(f)\ {\overset {\underset {\mathrm {def} }{}}{=}}\ \{z\in \mathbb {C} :f^{(k)}(z)\not \to \infty \ as\ k\to \infty \}}$
куда :

${\displaystyle \mathbb {C} }$ это набор комплексных чисел

${\displaystyle \ f^{(k)}(z)}$ это ${\displaystyle \ k}$ -складывать сочинение из ${\displaystyle f\,}$ с собой = итерация функции ${\displaystyle f\,}$

Отношение к множеству Фату

Заполненный набор Джулии - это (абсолютное) дополнение из привлекательный бассейн из бесконечность.
${\displaystyle K(f)=\mathbb {C} \setminus A_{f}(\infty )}$

В привлекательный бассейн из бесконечность один из компоненты набора Fatou.
${\displaystyle A_{f}(\infty )=F_{\infty }}$

Другими словами, заполненное множество Джулии - это дополнять безграничного Компонент Fatou:
${\displaystyle K(f)=F_{\infty }^{C}.}$

Связь Джулии, наполненного гарнитура Джулии и привлекательного бассейна бесконечности

В Юля набор это общий граница заполненного множества Джулия и привлекательный бассейн из бесконечность

${\displaystyle J(f)\,=\partial K(f)=\partial A_{f}(\infty )}$

куда :
${\displaystyle A_{f}(\infty )}$ обозначает привлекательный бассейн из бесконечность = внешний вид заполненного множества Джулии = множество точек выхода для ${\displaystyle f}$

${\displaystyle A_{f}(\infty )\ {\overset {\underset {\mathrm {def} }{}}{=}}\ \{z\in \mathbb {C} :f^{(k)}(z)\to \infty \ as\ k\to \infty \}.}$

Если в заполненном множестве Юля нет интерьер затем Юля набор совпадает с заполненным множеством Джулии. Это происходит, когда все критические точки ${\displaystyle f}$ являются предпериодическими. Такие критические точки часто называют Очки Мисюревича.

Позвоночник

• 

  Кролик Юля с корешком

• 

  Базилика Юлия с корешком

Вероятно, наиболее изученными полиномами являются те из формы ${\displaystyle f(z)=z^{2}+c}$, которые часто обозначают ${\displaystyle f_{c}}$, куда ${\displaystyle c}$ - любое комплексное число. В этом случае позвоночник ${\displaystyle S_{c}\,}$ заполненного набора Юля ${\displaystyle \ K\,}$ определяется как дуга между ${\displaystyle \beta \,}$-фиксированная точка и ${\displaystyle -\beta \,}$,

${\displaystyle S_{c}=\left[-\beta ,\beta \right]\,}$

с такими свойствами:

• позвоночник лежит внутри ${\displaystyle \ K\,}$.^[1] Это имеет смысл, когда ${\displaystyle K\,}$ подключен и полон^[2]
• позвоночник инвариантен при повороте на 180 градусов,
• spine - конечное топологическое дерево,
• Критическая точка ${\displaystyle z_{cr}=0\,}$ всегда принадлежит позвоночнику.^[3]
• ${\displaystyle \beta \,}$-фиксированная точка это точка приземления внешний луч нулевого угла ${\displaystyle {\mathcal {R}}_{0}^{K}}$,
• ${\displaystyle -\beta \,}$ это точка приземления внешний луч ${\displaystyle {\mathcal {R}}_{1/2}^{K}}$.

Алгоритмы построения позвоночника:

• подробная версия описан А. Дуади^[4]
• Упрощенная версия алгоритма:
  • соединять ${\displaystyle -\beta \,}$ и ${\displaystyle \beta \,}$ в ${\displaystyle K\,}$ по дуге,
  • когда ${\displaystyle K\,}$ имеет пустую внутреннюю часть, то дуга уникальна,
  • в противном случае выберите кратчайший путь, содержащий ${\displaystyle 0}$.^[5]

Изгиб ${\displaystyle R\,}$ :

${\displaystyle R\ {\overset {\underset {\mathrm {def} }{}}{=}}\ R_{1/2}\ \cup \ S_{c}\ \cup \ R_{0}\,}$

делит динамическую плоскость на две составляющие.

Изображений

• 

  Заполненный набор Юля для ж_c, c = φ − 2 = -0,38 ..., где φ означает Золотое сечение

• 

  Залил Юля без салона = Юля комплект. Это для c = i.

• 

  Заполненный набор Julia для c = -1 + 0,1 * i. Здесь множество Julia - это граница заполненного множества Julia.

• 

  Кролик дуади

• 

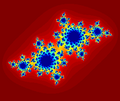
  Заполненный набор Джулии для c = −0,4 + 0,6i.

• 

  Заполненный набор Джулии для c = −0,8 + 0,156i.

• 

  Заполненный набор Julia для c = 0,285 + 0,01i.

• 

  Заполненный набор Julia для c = -1,476.

Имена

• самолет^[6]
• Кролик дуади
• Дракон
• базилика или Фрактал Сан-Марко
• цветная капуста
• дендрит
• Диск Зигеля

Примечания

1. Дуглас К. Равенел: Внешние углы в множестве Мандельброта: работа Дуади и Хаббарда. Университет Рочестера В архиве 2012-02-08 в Wayback Machine
2. Джон Милнор: Склеивание сетов Джулии: отработанный пример спаривания. Экспериментальная математика, том 13 (2004)
3. Сааед Закери: Биодоступность в квадратичных множествах Жюлиа I. Локально-связный случай
4. А. Дуади, «Алгоритмы вычисления углов в множестве Мандельброта», в «Хаотическая динамика и фракталы», М. Барнсли и С. Г. Демко, ред., Т. 2 заметок и отчетов по математике в науке и технике, стр. 155–168, Academic Press, Атланта, Джорджия, США, 1986.
5. К. М. Брукс, Х. Брюин: Темы из серии «Одномерная динамика»: Тексты студентов Лондонского математического общества (№ 62), стр. 257
6. Множество Мандельброта и связанные с ним множества Жюлиа, Герман Керхер

Рекомендации

1. Peitgen Heinz-Otto, Richter, P.H. : Красота фракталов: образы сложных динамических систем. Springer-Verlag 1986. ISBN  978-0-387-15851-8.
2. Бодил Браннер : Голоморфные динамические системы в комплексной плоскости. Департамент математики Технического университета Дании, MAT-Отчет № 1996-42.