Льюис Фрай Ричардсон - Lewis Fry Richardson

«Льюис Ричардсон» перенаправляется сюда. Для персонажа Hollyoaks см. Льюис Ричардсон (Hollyoaks).

Льюис Фрай Ричардсон
Льюис Фрай Ричардсон.png
Льюис Фрай Ричардсон, доктор наук, ФРС
Родившийся(1881-10-11)11 октября 1881 г.
Ньюкасл-апон-Тайн
Умер30 сентября 1953 г.(1953-09-30) (71 год)
Кильмун, Аргайл и Бьют
Гражданствообъединенное Королевство
Альма-матерBootham School
Даремский колледж науки
Королевский колледж, Кембридж
ИзвестенФракталы
Конфликт моделирование
Экстраполяция Ричардсона
НаградыЧлен Королевского общества[1]
Научная карьера
Поляматематик
физик
метеоролог
психолог
УчрежденияНациональная физическая лаборатория
Национальная торфяная промышленность
Университетский колледж Аберистуита
Метеорологическое бюро
Технический колледж Пейсли
ВлиянияКарл Пирсон
Г. Ф. С. Сирл
Дж. Дж. Томсон
Под влияниемБенуа Мандельброт

Льюис Фрай Ричардсон, ФРС[1] (11 октября 1881 г. - 30 сентября 1953 г.) был английским математиком, физик, метеоролог, психолог и пацифист кто был пионером современных математических методов прогнозирования погоды и применения аналогичных методов для изучения причин войн и способов их предотвращения. Он также известен своей новаторской работой в области фракталы и метод решения система линейных уравнений известный как модифицированная итерация Ричардсона.[2]

Ранние годы

Льюис Фрай Ричардсон был младшим из семи детей, рожденных Кэтрин Фрай (1838–1919) и Дэвидом Ричардсоном (1835–1913). Они были зажиточными Квакер В семье Дэвида Ричардсона успешно работает дубильный и кожевенный бизнес.[3]

В 12 лет его отправили в Квакер школа-интернат, Bootham School[4][5] в Йорк, где получил научное образование, что стимулировало активный интерес к естественная история. В 1898 году он продолжил Даремский колледж науки (колледж Даремский университет ) где он проходил курсы математическая физика, химия, ботаника, и зоология. В 1900 году он приступил к Королевский колледж, Кембридж, где он изучал физику в естественных науках (среди прочих) Дж. Дж. Томсон и получил диплом с отличием в 1903 году.[6] В 47 лет он получил степень доктора математической психологии Лондонский университет.[7]

Карьера

Трудовая жизнь Ричардсона представляла его эклектические интересы:[8]

В 1926 году он был избран в Товарищество Королевское общество[1][9]

Пацифизм

Квакерские убеждения Ричардсона повлекли за собой пацифизм что освободило его от военной службы во время Первая Мировая Война как отказник по убеждениям, хотя впоследствии это лишило его права занимать какую-либо академическую должность. Ричардсон работал с 1916 по 1919 год в Скорая помощь друзей прикреплен к 16-й французской пехотной дивизии. После войны он вернулся в Метеорологическое управление, но был вынужден уйти в отставку по соображениям совести, когда оно было объединено в Метеорологическое управление. Министерство авиации в 1920 году. Впоследствии он сделал карьеру на окраине академического мира, прежде чем уйти в отставку в 1940 году, чтобы исследовать свои собственные идеи. Его пацифизм имел прямые последствия для его исследовательских интересов. В соответствии с Томас Кёрнер,[10] Открытие, что его метеорологическая работа представляет ценность для разработчиков химического оружия, заставило его отказаться от всех своих усилий в этой области и уничтожить результаты, которые он еще не опубликовал.

Прогноз погоды

Интерес Ричардсона к метеорология побудил его предложить схему для прогноз погоды решением дифференциальные уравнения, метод, используемый в настоящее время, хотя, когда он опубликовал Прогноз погоды с помощью числового процесса в 1922 году подходящие быстрые вычисления были недоступны. Он так описал свои идеи (его «компьютеры» - это люди):

«После стольких напряженных рассуждений можно ли играть с фантазией? Представьте себе большой зал, похожий на театр, за исключением того, что круги и галереи проходят прямо через пространство, обычно занимаемое сценой. Стены этой комнаты окрашены, чтобы образовать карта земного шара: на потолке изображены северные полярные регионы, Англия - в галерее, тропики - в верхнем круге, Австралия - на бельевом круге и Антарктика - в яме.

Множество компьютеров работают с погодой в той части карты, где каждый находится, но каждый компьютер занимается только одним уравнением или частью уравнения. Работу каждого региона координирует чиновник более высокого ранга. Множество маленьких «ночных знаков» отображают мгновенные значения, так что соседние компьютеры могут их прочитать. Таким образом, каждое число отображается в трех смежных зонах, чтобы поддерживать связь с севером и югом на карте.

Из пола ямы высокий столб поднимается на половину высоты зала. На его вершине находится большая кафедра. Здесь сидит человек, отвечающий за весь театр; его окружают несколько помощников и посыльных. Одна из его обязанностей - поддерживать одинаковую скорость прогресса во всех частях земного шара. В этом отношении он подобен дирижеру оркестра, инструментами которого являются логарифмические линейки и счетные машины. Но вместо того, чтобы размахивать дубинкой, он направляет луч розового света на любую область, которая идет впереди остальных, и луч голубого света на тех, кто находится позади.

Четыре старших клерка на центральной кафедре собирают прогноз погоды в будущем так же быстро, как и вычисляют, и отправляют ее пневматическим транспортером в тихую комнату. Там его закодируют и позвонят на радиопередающую станцию. Мессенджеры несут груды использованных компьютерных форм на склад в подвале.

В соседнем здании есть исследовательский отдел, где придумывают улучшения. Но прежде чем вносить какие-либо изменения в сложную рутину компьютерного театра, необходимо провести множество экспериментов в небольшом масштабе. В подвале энтузиаст наблюдает водовороты в жидкой подкладке огромной вращающейся чаши, но пока что арифметика показывает лучший способ. В другом здании все обычные финансовые, корреспондентские и административные офисы. Снаружи есть игровые поля, дома, горы и озера, поскольку считалось, что те, кто рассчитывает погоду, должны свободно дышать ею »(Richardson 1922).

(Слово «компьютеры» используется здесь в своем первоначальном значении - люди, которые выполняли вычисления, а не машины. «Калькулятор» также относился к людям в то время.)

Когда новости о первом прогнозе погоды от первого современного компьютера, ENIAC, был получен Ричардсоном в 1950 году, он ответил, что результаты были «огромным научным достижением». Первые расчеты 24-часового прогноза заняли у ENIAC почти 24 часа.[11]

Он также интересовался атмосферный турбулентность и провел много земных экспериментов. В Число Ричардсона, а безразмерный параметр теории турбулентности назван в его честь. Он классно резюмировал турбулентность в стихах в стихах. Прогноз погоды с помощью числового процесса (стр 66):[12]

У больших вихрей есть маленькие вихри, которые питаются своей скоростью,

и маленькие завихрения имеют меньшие завихрения и так далее до вязкости.

[Игра на Сифонаптера, Огастес Де Морган переформулировка Джонатан Свифт «У больших блох есть маленькие блохи на спине, чтобы их кусать, А у маленьких блох есть блохи поменьше, и так до бесконечности». (Бюджет парадоксов, 1915)].

Попытка Ричардсона численного прогноза

Одним из самых знаменитых достижений Ричардсона является его попытка задним числом спрогнозировать погоду на один день - 20 мая 1910 года - с помощью прямых вычислений. В то время метеорологи составляли прогнозы в основном путем поиска похожих погодных условий на основе прошлых записей, а затем экстраполировали их на будущее. Ричардсон попытался использовать математическую модель основных характеристик атмосферы и использовать данные, полученные в определенное время (7 часов утра), для расчета погоды через шесть часов. ab initio. Как метеоролог Питер Линч проясняет,[13] Прогноз Ричардсона резко провалился: он предсказал огромное повышение давления на 145 гектопаскалей (4,3 дюйма ртутного столба) за шесть часов, когда давление фактически было более или менее статичным. Однако подробный анализ, проведенный Линчем, показал, что причиной была неспособность применить к данным методы сглаживания, которые исключают нефизические скачки давления. Когда они применяются, прогноз Ричардсона оказывается по существу точным - замечательное достижение, учитывая, что расчеты проводились вручную, а Ричардсон служил в квакерском отделении скорой помощи на севере Франции.

Математический анализ войны

Ричардсон также применил свои математические навыки на службе своих пацифистских принципов, в частности, для понимания основ международного конфликта. По этой причине он теперь считается инициатором или соинициатором (с Куинси Райт и Питирим Сорокин а также другие, такие как Кеннет Боулдинг, Анатолий Рапапорт и Адам Кёрл ), научного анализа конфликта - междисциплинарной темы количественной и математической социальной науки, посвященной систематическому исследованию причин войны и условий мира. Как и в случае с погодой, он анализировал войну, используя в основном дифференциальные уравнения и теорию вероятностей. Рассматривая вооружение двух наций, Ричардсон постулировал идеализированную систему уравнений, согласно которой скорость наращивания вооружений нации прямо пропорциональна количеству вооружений, имеющихся у ее соперника, а также недовольству, которое испытывает к сопернику, и отрицательно пропорциональна количеству вооружений. количество оружия у него уже есть. Решение этой системы уравнений позволяет сделать проницательные выводы относительно природы, а также устойчивости или нестабильности различных гипотетических условий, которые могут возникнуть между странами.

Он также создал теорию о том, что склонность к войне между двумя странами была функцией длины их общей границы. И в Оружие и небезопасность (1949), и Статистика смертельных ссор (1960) он стремился проанализировать причины войны статистически. Он оценил следующие факторы: экономика, язык и религия. В предисловии к последнему он писал: «В мире существует множество блестящих, остроумных политических дискуссий, которые не приводят к твердым убеждениям. Моя цель была иная: а именно исследовать несколько понятий с помощью количественных методов в надежде получения надежного ответа ".

В Статистика смертельных ссор Ричардсон представил данные практически по каждой войне с 1815 по 1945 год. В результате он выдвинул гипотезу база 10 логарифмическая шкала для конфликтов. Другими словами, маленьких боев, в которых погибает всего несколько человек, намного больше, чем больших, убивающих многих. Хотя размер конфликта невозможно предсказать заранее - действительно, невозможно дать верхний предел для ряда - в целом они формируют распределение Пуассона. В меньшем масштабе он продемонстрировал ту же картину для групповых убийств в Чикаго и Шанхае. Другие отметили, что аналогичные статистические закономерности возникают часто, будь то запланированные (лотереи с гораздо большим количеством мелких выплат, чем крупных выигрышей) или естественная организация (в небольших городах есть продуктовые магазины, а в больших городах с супермаркетами).

Исследование протяженности береговой линии и границ

Основная статья: Парадокс береговой линии

Ричардсон решил найти связь между вероятность двух стран, идущих на войну, и протяженность их общей границы. Однако при сборе данных он обнаружил, что существуют значительные различия в опубликованных длинах международных границ. Например, расстояние между Испанией и Португалией было по-разному обозначено как 987 или 1214 км, а между Нидерландами и Бельгией - как 380 или 449 км.[14]

Причина этих несоответствий - "парадокс береговой линии ". Предположим, что побережье Британии измеряется с помощью линейки длиной 200 км, при этом указывается, что оба конца линейки должны касаться берега. Теперь разрежьте линейку пополам и повторите измерение, затем повторите:

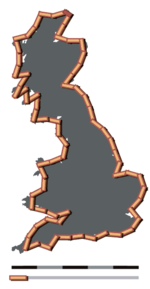
Британия-фрактал-береговая линия-200км.pngБритания-фрактал-береговая линия-100км.pngБритания-фрактал-береговая линия-50 км.png

Обратите внимание: чем меньше линейка, тем длиннее береговая линия. Можно было предположить, что эти значения сходятся к конечный число, представляющее истинную длину береговой линии. Однако Ричардсон продемонстрировал, что это не так: измеренная длина береговой линии и других природных объектов неограниченно увеличивается по мере уменьшения единицы измерения.[15] В настоящее время это известно как Эффект Ричардсона.[16]

В то время научное сообщество проигнорировало исследования Ричардсона. Сегодня это считается элементом начала современного изучения фракталы. Исследование Ричардсона цитировал математик Бенуа Мандельброт в его статье 1967 г. Какова длина побережья Британии? Ричардсон определил значение (от 1 до 2), которое описывает изменения (с увеличением детализации измерений) в наблюдаемой сложности для конкретной береговой линии; это значение послужило образцом для концепции фрактальная размерность.[17]

Патенты на обнаружение айсбергов

В апреле 1912 г., вскоре после гибели корабля Титаник, Richardson зарегистрировал патент на обнаружение айсбергов с помощью акустических эхолокация в воздухе. Через месяц он зарегистрировал аналогичный патент на акустическую эхолокацию в воде, предвосхищая изобретение сонар к Поль Ланжевен и Роберт Бойл 6 лет спустя.[18]

В популярной культуре

Вымышленная версия Ричардсона по имени Уоллес Райман играет ключевую роль в Джайлз Фоден роман Турбулентность.[19]

Ричардсон упоминается в Джон Бруннер работа, Стой на Занзибаре куда Статистика смертельных ссор используется как аргумент, что войны неизбежны.

Работа Ричардсона также упоминается в Пол Андерсон спекулятивная фантастическая повесть, Короли, которые умирают.

Знаменитая цитата Ричардсона «У больших водоворотов есть маленькие завихрения, которые подпитываются их скоростью; маленькие водовороты имеют меньшие завихрения и так далее до вязкости» упоминается в получившей признание критиков песне «Dots & Lines», написанной и исполненной лауреатом Грэмми лириком / рэпером Лупе. Фиаско.

Личная жизнь

В 1909 году он женился на Дороти Гарнетт (1885–1956), дочери математика и физика. Уильям Гарнетт.[20] У них не было детей из-за несовместимости групп крови, но они усыновили двух сыновей и дочь в период с 1920 по 1927 год.[21]

Племянник Ричардсона Ральф Ричардсон стал известным актером. Его внучатый племянник (через старшего брата его жены Дороти, (Джеймс Клерк) Максвелл Гарнетт, C.B.E.), Джулиан Хант С 1992 по 1997 год он стал метеорологом, генеральным директором и главным исполнительным директором Британского метеорологического бюро.[22] Внучатая племянница того же происхождения - бывший политик. Вирджиния Боттомли, теперь баронесса Боттомли.[23][24]

Наследие

С 1997 г. Медаль Льюиса Фрая Ричардсона был награжден Европейский союз геонаук за «исключительный вклад в нелинейную геофизику в целом» (EGS до 2003 г.[25] и EGU с 2004 г.).[26]

Победителями стали:

С 1959 г. в г. Ланкастерский университет назвал Институт Ричардсона, который проводит междисциплинарные исследования мира и конфликтов в духе Льюиса Фрая Ричардсона.[28]

Смотрите также

Примечания

  1. ^ а б c Голд, Э. (1954). «Льюис Фрай Ричардсон. 1881–1953». Уведомления о некрологе членов Королевского общества. 9 (1): 216–235. Дои:10.1098 / рсбм.1954.0015. JSTOR  769208. S2CID  191485345.
  2. ^ О'Коннор, Джон Дж.; Робертсон, Эдмунд Ф., "Льюис Фрай Ричардсон", Архив истории математики MacTutor, Сент-Эндрюсский университет.
  3. ^ Хант, стр. xiv
  4. ^ Регистр школы Bootham. Йорк, Англия: BOSA. 2011 г.CS1 maint: ref = harv (связь)
  5. ^ Оксфордский национальный биографический словарь[постоянная мертвая ссылка ]
  6. ^ Хант, стр. xv
  7. ^ "Льюис Фрай Ричардсон" (PDF). Архивировано из оригинал (PDF) 5 мая 2016 г.. Получено 30 января 2019.
  8. ^ Эшфорд 1985, главы 3–7
  9. ^ "Цитата выборов Королевского общества EC / 1926/21". Королевское общество. 1926. Архивировано из оригинал 13 января 2013 г.. Получено 21 января 2008.
  10. ^ Кёрнер, Т. (1996). «Квакерский математик» и «Ричардсон о войне», главы 8 и 9 в Удовольствие от счета (Кембридж, США)
  11. ^ Питер Линч (2008). «Истоки компьютерного прогнозирования погоды и моделирования климата» (PDF). Журнал вычислительной физики. Университет Майами. 227 (7): 3436. Bibcode:2008JCoPh.227.3431L. Дои:10.1016 / j.jcp.2007.02.034. Архивировано из оригинал (PDF) 8 июля 2010 г.. Получено 23 ноября 2010.
  12. ^ Ричардсон, Льюис Фрай (1922). Прогноз погоды с помощью численных процессов. Бостон: Издательство Кембриджского университета. п.66. ISBN  9780511618291. Получено 23 февраля 2019.
  13. ^ Линч, П. (2006). Появление численных прогнозов погоды (Кембридж, США).
  14. ^ Льюис Ф. Ричардсон (1961). «Проблема смежности: приложение к статистике смертельных ссор». Общие системы: Ежегодник Общества развития общей теории систем. Анн-Арбор, Мичиган: Общество [1956–: Общество общих системных исследований. 6 (139): 139–187. ISSN  0072-0798. OCLC  1429672. В предыдущем разделе интегралы были взяты вокруг простых геометрических фигур в качестве предварительного анализа границ, показанных на политических картах. Возникло смущающее сомнение относительно того, были ли фактические границы настолько сложными, чтобы опровергнуть эту многообещающую теорию. Для решения этого вопроса было проведено специальное расследование. Обнаружились некоторые странные особенности; тем не менее, общая коррекция оказалась возможной. Теперь о результатах будет сообщено. ... В качестве объяснения того, как случай может возникнуть в мире, который он считал строго детерминированным, Хери Пуанкаре * (без даты) обратил внимание на незначительные причины, которые производили очень заметные следствия. Морские побережья служат хорошей иллюстрацией.CS1 maint: location (связь)
  15. ^ Фракталы и фрактальное измерение (веб-сайт Университета Вандербильта, по состоянию на 30 января 2008 г.) В архиве 13 мая 2008 г. Wayback Machine
  16. ^ "Эффект Ричардсона". www.futilitycloset.com. 2 декабря 2013 г.
  17. ^ П. Г. Дразин, «Фракталы»; Сборник статей Льюиса Фрая Ричардсона, том 1; Cambridge University Press, 1993; п. 45.
  18. ^ Майкл А. Эйнсли Принципы моделирования характеристик сонара, Springer, 2010 г. ISBN  3-540-87661-8, стр. 10
  19. ^ Foden
  20. ^ Уильям Гарнетт (1850–1932) - Краткая биография на веб-сайте Британского общества истории математики (по состоянию на 21 января 2008 г.)
  21. ^ Эшфорд (2004)
  22. ^ https://www.independent.co.uk/news/world/lewis-fry-richardsons-weather-forecasts-changed-the-world-but-could-his-predictions-of-war-do-the-9679295. html
  23. ^ https://www.independent.co.uk/news/obituaries/obituary-john-garnett-1239782.html
  24. ^ «Архивная копия». Архивировано из оригинал 30 апреля 2018 г.. Получено 29 апреля 2018.CS1 maint: заархивированная копия как заголовок (связь)
  25. ^ http://www.egu.eu/egs/award6s.htm
  26. ^ http://www.egu.eu/awards-medals/lewis-fry-richardson
  27. ^ Текст лекции лауреата 2007 года «От завитушек к глобальной атмосфере»
  28. ^ [1]

Рекомендации

внешняя ссылка