Лента Мебиуса - Möbius strip



В математика, а Лента Мебиуса, группа, или же петля (нас: /ˈмoʊбяəs,ˈмeɪ-/ Минздрав-пчелы-əs, МАЙ-, Великобритания: /ˈмɜːбяəs/;[1] Немецкий: [ˈMøːbi̯ʊs]), также пишется Мебиус или же Мебиус, это поверхность только с одной стороны (при встраивании в трехмерную Евклидово пространство ) и только один граничная кривая. Лента Мебиуса - простейшая неориентируемый поверхность. Это может быть реализовано как линейчатая поверхность. Его открытие независимо приписывается немецким математикам. Иоганн Бенедикт Листинг и Август Фердинанд Мёбиус в 1858 г.,[2][3][4][5] хотя похожие структуры можно увидеть в римских мозаиках c. 200–250 гг. Нашей эры.[6][7] Мёбиус опубликовал свои результаты в статьях «Theorie der elementaren Verwandtschaft» (1863) и «Ueber die Bestimmung des Inhaltes eines Polyëders» (1865).[8]
Пример ленты Мебиуса может быть создан, если взять полоску бумаги и повернуть один конец до половины, а затем соединить концы, чтобы образовать петлю; его граница представляет собой простую замкнутую кривую, которую можно проследить одним несвязанный нить. Любой топологическое пространство гомеоморфный этому примеру также называется лентой Мёбиуса, что позволяет использовать самые разнообразные геометрические реализации в виде поверхностей с определенный размер и форма. Например, любой прямоугольник можно приклеить по левому краю к правому краю с изменением ориентации. Некоторые, но не все, из них можно гладко смоделировать как поверхности в Евклидово пространство. Тесно родственная, но не гомеоморфная поверхность - это полная открытая лента Мёбиуса, поверхность без границ, на которой ширина полосы бесконечно расширяется, чтобы стать евклидовой линией.
Половина по часовой стрелке дает вложение ленты Мёбиуса, которую нельзя сдвинуть или растянуть, чтобы получить полувыворот против часовой стрелки; таким образом, лента Мебиуса, вложенная в евклидово пространство, является хиральный объект с правшей или левшей. Ленту Мёбиуса также можно врезать, скручивая полоску любое нечетное количество раз или завязывая и скручивая полоску перед соединением ее концов.
обнаружение алгебраические уравнения вырезать ленту Мёбиуса несложно, но эти уравнения не описывают ту же геометрическую форму, что и модель из скрученной бумаги выше. Такие бумажные модели бывают складывающиеся поверхности имея ноль Гауссова кривизна, и может быть описан дифференциально-алгебраические уравнения.[9]
В Эйлерова характеристика ленты Мёбиуса нуль.

Характеристики
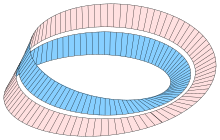
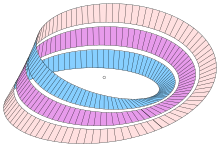
Лента Мёбиуса обладает несколькими любопытными свойствами. Линия, проведенная вдоль края, проходит полный круг до точки, противоположной начальной точке. Если продолжить, линия вернется в исходную точку и будет вдвое длиннее исходной полосы: эта единственная непрерывная кривая пересекает всю границу.
Если разрезать ленту Мебиуса по центральной линии ножницами, получается одна длинная полоса с двумя полными поворотами, а не две отдельные полосы; в результате получается не лента Мёбиуса, а гомеоморфная цилиндру. Это происходит потому, что исходная полоса имеет только один край, вдвое длиннее исходной полосы. Обрезка создает второй независимый край такой же длины, по половине с каждой стороны ножниц. Если разрезать эту новую более длинную полоску посередине, получатся две полоски, намотанные друг на друга, каждая с двумя полными витками.
Если полоса разрезается примерно на треть от края, получается две полосы: центральная треть - более тонкая полоса Мебиуса той же длины, что и исходная полоса. Другой - тонкая полоска с двумя полными витками, район края исходной полосы, вдвое превышающей длину исходной полосы.[2]
Другие аналогичные полосы могут быть получены аналогичным соединением полос с двумя или более полувинками вместо одного. Например, полоса с тремя полусвитами при продольном разделении становится скрученной полосой, завязанной в трилистник. (Если этот узел распутан, полоска имеет восемь полувручок.) Полоса с N полувручения, когда делятся пополам, становится полосой с N + 1 полный поворот.[2] Дополнительные скрутки и повторное соединение концов дают фигуры, называемые парадромные кольца.
Геометрия и топология

Один из способов представить ленту Мёбиуса, вложенную в трехмерное евклидово пространство, - это параметризация:
за и . Это создает полосу Мебиуса шириной 1, центральная окружность которой имеет радиус 1, лежит в -плоскость с центром в . Параметр ты бегает по полосе, пока v переходит от одного края к другому.
В цилиндрические полярные координаты , неограниченный вариант ленты Мёбиуса можно представить уравнением:
Широчайшее изометрическое вложение в 3-х пространстве
Если гладкая полоса Мебиуса в трех пространствах является прямоугольной, то есть создана путем отождествления двух противоположных сторон геометрического прямоугольника с изгибом, но без растяжения поверхности, то такое вложение, как известно, возможно, если соотношение сторон геометрического прямоугольника прямоугольник больше чем , с обозначением более коротких сторон. (При меньшем соотношении сторон неизвестно, возможно ли плавное встраивание.) Поскольку соотношение сторон уменьшается в сторону , любое такое вложение, кажется, приближается к форме, которую можно представить как полосу из трех равносторонних треугольников, сложенных друг над другом и образующих равносторонний треугольник.
Если лента Мёбиуса в трехмерном пространстве непрерывно дифференцируема только один раз (класс C1), однако теорема Нэша-Койпера показывает, что нижней оценки не существует.
Метод изготовления ленты Мебиуса из прямоугольной полосы, слишком широкой, чтобы ее можно было просто скрутить и соединить (например, прямоугольник длиной всего одну единицу и ширину одну единицу), заключается в том, чтобы сначала согнуть широкое направление вперед и назад, используя четное количество сгибов - «складка гармошкой» - так, чтобы сложенная полоса стала достаточно узкой, чтобы ее можно было скручивать и соединять, как можно соединить одну достаточно длинную полоску.[10] С двумя складками, например, 1 × 1 полоса станет 1 × ⅓ сложенная полоса, чья поперечное сечение имеет форму буквы «N» и останется буквой «N» после полуворота. Эта сложенная полоса, в три раза длиннее ее ширины, будет достаточно длинной, чтобы затем соединиться на концах. Этот метод в принципе работает, но становится непрактичным после достаточно большого количества складок, если используется бумага. Используя обычную бумагу, эту конструкцию можно сложенная квартира, со всеми слоями бумаги в одной плоскости, но математически, возможно ли это без растяжения поверхности прямоугольника, не ясно.[11]
Топология

Топологически полосу Мёбиуса можно определить как квадрат с его верхней и нижней сторон идентифицированный отношением за , как на схеме.
Менее используемое представление ленты Мёбиуса - это топологический фактор тора.[12] Тор можно построить как квадрат с краями, обозначенными как (приклеить слева направо) и (приклеиваем снизу вверх). Если один, то также идентифицировал (Икс, у) ~ (у, Икс), то получаем ленту Мёбиуса. Диагональ квадрата (точки (Икс, Икс) где обе координаты совпадают) становится границей ленты Мёбиуса и несет структуру орбифолда, которая геометрически соответствует "отражению" - геодезические (прямые линии) в ленте Мебиуса отражаются от края обратно в полосу. Условно это записывается как T2/ S2 - 2-тор, факторный групповое действие из симметричная группа на двух буквах (координаты переключения), и его можно рассматривать как конфигурационное пространство двух неупорядоченных точек на окружности, возможно, одинаковых (ребро соответствует одинаковым точкам), а тор соответствует двум упорядоченным точкам на окружности.
Лента Мебиуса - это двумерная компактный коллектор (т.е. поверхность ) с краем. Это стандартный пример поверхности, которая не ориентируемый. Фактически, полоса Мёбиуса является воплощением топологического феномена неориентируемость. Это связано с тем, что двумерные формы (поверхности) являются формами наименьшей размерности, для которых возможна неориентируемость, а полоса Мёбиуса является Только поверхность, которая топологически является подпространством каждый неориентируемая поверхность. В результате любая поверхность неориентируема тогда и только тогда, когда она содержит ленту Мёбиуса в качестве подпространства.
Полоса Мёбиуса также является стандартным примером, используемым для иллюстрации математической концепции пучок волокон. В частности, это нетривиальное расслоение над окружностью S1 с волокном, равным единичный интервал, я = [0, 1]. Глядя только на край ленты Мёбиуса, можно получить нетривиальные две точки (или Z2) связать S1.
Компьютерная графика
Простая конструкция ленты Мёбиуса, которую можно использовать для ее изображения в компьютерной графике или пакетах моделирования:
- Возьмите прямоугольную полоску. Поверните его вокруг фиксированной точки не в его плоскости. На каждом шаге также вращайте полосу вдоль линии в ее плоскости (линии, разделяющей полосу пополам) и перпендикулярно основному радиусу орбиты. Поверхность, образующаяся за один полный оборот, является лентой Мёбиуса.
- Возьмите ленту Мёбиуса и разрежьте ее по середине. Это формирует новую полосу, которая представляет собой прямоугольник, соединенный путем поворота одного конца на целый оборот. Если снова разрезать его посередине, получится две взаимосвязанные полноповоротные полоски.
Геометрия открытой ленты Мёбиуса
В открытая лента Мёбиуса формируется путем удаления граница стандартной ленты Мебиуса. Он построен из множества S = { (Икс, у) ∈ р2 : 0 ≤ Икс ≤ 1 и 0 < у < 1 } путем выявления (склейки) точек (0, у) и (1, 1 − у) для всех 0 < у < 1.
Он может быть построен как поверхность постоянного положительного, отрицательного или нулевого (гауссова) кривизна. В случаях отрицательной и нулевой кривизны лента Мёбиуса может быть построена как (геодезически) полная поверхность, что означает, что все геодезические («прямые» на поверхности) могут быть неограниченно продолжены в любом направлении.
Постоянная отрицательная кривизна:Подобно плоскости и открытому цилиндру, открытая лента Мёбиуса допускает не только полную метрику постоянной кривизны 0, но и полную метрику постоянной отрицательной кривизны, скажем −1. Один из способов увидеть это - начать с модель верхней полуплоскости (Пуанкаре) из гиперболическая плоскость ℍ, а именно ℍ = {(Икс, у) ∈ ℝ2 | у > 0} с Риманова метрика данный (dx2 + dy2) / у2. Изометриями этой метрики, сохраняющими ориентацию, являются все отображения ж : ℍ → ℍ формы ж(z) := (az + б) / (cz + d), куда а, б, c, d настоящие числа удовлетворяют объявление − до н.э = 1. Здесь z это комплексное число с Я(z) > 0, и мы определили ℍ с {z ∈ ℂ | Я(z) > 0} снабженный упомянутой римановой метрикой. Тогда одна изометрия с обращением ориентации грамм из ℍ дан кем-то грамм(z) := −z, куда z обозначает комплексное сопряжение z. Из этих фактов следует, что отображение час : ℍ → ℍ данный час(z) := −2⋅z является обращающей ориентацию изометрией ℍ который порождает бесконечную циклическую группу грамм изометрий. (Его можно выразить как час(z) = (√2я z + 0) / (0z − я/√2), а его квадрат - изометрия час(час(z)) := 4⋅z, который можно выразить как (2z + 0) / (0z + 1⁄2).) Частное ℍ / грамм действия этой группы, как легко видеть, топологически является лентой Мёбиуса. Но также легко проверить, что он полный и некомпактный, с постоянной отрицательной кривизной, равной −1.
Группа изометрий этой ленты Мёбиуса одномерна и изоморфна специальной ортогональной группе SO (2).
(Постоянная) нулевая кривизна:Это также может быть построено как целая поверхность, начиная с части плоскости. р2 определяется 0 ≤ у ≤ 1 и определение (Икс, 0) с (−Икс, 1) для всех Икс в р (реалы). Результирующая метрика превращает открытую ленту Мёбиуса в (геодезически) полную плоскую поверхность (т.е. имеющую гауссову кривизну, равную 0 всюду). Это единственная метрика на ленте Мебиуса, с точностью до равномерного масштабирования, которая является одновременно плоской и полной.
Группа изометрий этой ленты Мёбиуса одномерна и изоморфна ортогональной группе SO (2).
Постоянная положительная кривизна:Лента Мёбиуса постоянной положительной кривизны не может быть полной, поскольку известно, что единственными полными поверхностями постоянной положительной кривизны являются сфера и проективная плоскость. Проективная плоскость п2 постоянной кривизны +1 может быть построена как частное единичной сферы S2 в р3 по антиподальной карте А: S2 → S2, определяется А(Икс, у, z) = (−Икс, −у, −z). Открытая лента Мёбиуса гомеоморфна проективной плоскости с проколом, т. Е. п2 с удалением одной точки. Это можно рассматривать как наиболее близкое к тому, что полоса Мебиуса постоянной положительной кривизны может стать полной поверхностью: всего в одной точке.
Группа изометрий этой ленты Мёбиуса также одномерна и изоморфна ортогональной группе O (2).
Пространство неориентированных линий на плоскости равно диффеоморфный открытой ленте Мебиуса.[13] Чтобы понять почему, позвольте L(θ) обозначим прямую, проходящую через начало координат под углом θ к положительной оси абсцисс. Для каждого L(θ) есть семья п(θ) всех прямых на плоскости, перпендикулярных L(θ). Топологически семья п(θ) - это просто строка (потому что каждая строка в п(θ) пересекает линию L(θ) всего в одной точке). Таким образом, как θ увеличивается в диапазоне 0° ≤ θ < 180°, линия L(θ) представляет собой количество отдельных линий на плоскости. Но когда θ достигает 180 °, L(180 °) идентично L(0), поэтому семейства п(0 °) и п(180 °) перпендикулярных линий также являются идентичными семействами. Линия L(0 °), однако, вернулась к себе как L(180°) указал в противоположном направлении. Каждая линия на плоскости соответствует ровно одной линии в некотором семействе п(θ) ровно для одного θ, за 0° ≤ θ < 180°, и п(180 °) идентично п(0 °), но возвращается в противоположном направлении. Это гарантирует, что пространство всех линий на плоскости - объединение всех L(θ) за 0° ≤ θ ≤ 180° - открытая лента Мебиуса.
Группа биективных линейных преобразований GL (2, р) самолета себе (реальный 2 × 2 матриц с ненулевым определителем) естественным образом индуцирует биекции пространство линий на плоскости самому себе, которые образуют группу самогомеоморфизмов пространства прямых. Следовательно, эта же группа образует группу самогомеоморфизмов ленты Мёбиуса, описанную в предыдущем абзаце. Но на пространстве прямых на плоскости нет метрики, инвариантной относительно действия этой группы гомеоморфизмов. В этом смысле пространство прямых на плоскости не имеет естественной метрики.
Это означает, что лента Мёбиуса обладает естественным 4-мерным Группа Ли самогомеоморфизмов, задаваемых GL (2, р), но эта высокая степень симметрии не может быть представлена как группа изометрий какой-либо метрики.
Лента Мебиуса с круглой границей
Край, или граница, ленты Мёбиуса есть гомеоморфный (топологически эквивалентно) круг. При обычных вложениях полосы в евклидово пространство, как указано выше, граница не является истинной окружностью. Однако возможно вставлять лента Мебиуса в трех измерениях, так что граница представляет собой идеальный круг, лежащий в некоторой плоскости. Например, см. Рисунки 307, 308 и 309 раздела «Геометрия и воображение».[14]
Гораздо более геометрическое вложение начинается с минимального Бутылка Клейна погруженный в 3-сферу, как обнаружил Блейн Лоусон. Затем мы берем половину этой бутылки Клейна, чтобы получить ленту Мёбиуса, вложенную в 3-сферу (единичную сферу в 4-пространстве). Результат иногда называют «суданской лентой Мёбиуса».[15] где «суданец» относится не к стране Судан но с именами двух топологов, Сью Гудман и Дэниела Азимова. Применение стереографической проекции к суданской группе помещает ее в трехмерное пространство, как показано ниже - можно найти версию Джорджа Фрэнсиса. здесь.
Из минимальной бутылки Клейна Лоусона мы выводим вложение ленты в 3-сфера S3, рассматриваемый как подмножество C2, который геометрически совпадает с р4. Наносим углы на карту η, φ к комплексным числам z1, z2 через
Здесь параметр η работает от 0 до π и φ работает от 0 до 2π. С |z1|2 + |z2|2 = 1, вложенная поверхность целиком лежит в S3. Граница полосы определяется выражением |z2| = 1 (соответствует η = 0, π), который, очевидно, представляет собой круг на 3-сфере.
Чтобы получить вложение ленты Мёбиуса в р3 одна карта S3 к р3 через стереографическая проекция. Точкой проецирования может быть любая точка на S3 который не лежит на вложенной ленте Мёбиуса (это исключает все обычные точки проекции). Один из возможных вариантов: . Стереографические проекции преобразуют круги в круги и сохраняют круговую границу полосы. В результате получается гладкое вложение ленты Мёбиуса в р3 с круглым краем и без самопересечений.
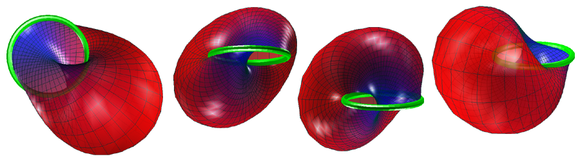
Суданская лента Мебиуса в трех сферах S3 геометрически является расслоением над большим кругом, слои которого представляют собой большие полукруги. Наиболее симметричное изображение стереографической проекции этой полосы в р3 получается путем использования точки проекции, которая лежит на большом круге, проходящем через середину каждого из полукругов. Каждый выбор такой точки проекции приводит к изображению, совпадающему с любым другим. Но поскольку такая точка проекции находится на самой полосе Мебиуса, два аспекта изображения значительно отличаются от случая (проиллюстрированного выше), когда точка находится не на полосе: 1) изображение в р3 не полная лента Мебиуса, а скорее лента с одной удаленной точкой (от ее средней линии); и 2) образ неограничен - и по мере того, как он удаляется от источника р3, он все больше приближается к плоскости. Тем не менее, эта версия стереографического изображения имеет группу из 4 симметрий в р3 (он изоморфен Кляйн 4-группа ) по сравнению с проиллюстрированной выше ограниченной версией, имеющей группу симметрий единственной группы порядка 2. (Если все симметрии, а не только сохраняющие ориентацию изометрии р3 допустимы, количество симметрий в каждом случае удваивается.)
Но наиболее геометрически симметричной версией из всех является оригинальная суданская лента Мебиуса в трех сферах. S3, где его полная группа симметрий изоморфна группе Ли O (2). Имея бесконечную мощность (мощность континуум ), это намного больше, чем группа симметрии любого возможного вложения ленты Мёбиуса в р3.
Проективная геометрия
С помощью проективная геометрия, открытую ленту Мёбиуса можно описать как множество решений полиномиального уравнения. Добавление полиномиального неравенства приводит к замкнутой ленте Мёбиуса. Они связывают ленты Мебиуса с геометрией линейные пакеты и работа взрыв в алгебраическая геометрия.
Реальная проективная линия это набор по модулю масштабирования. То есть точка в является классом эквивалентности вида
Каждый класс эквивалентности с имеет уникального представителя, вторая координата которого равна 1, а именно . Эти точки образуют копию евклидовой линии . Однако класс эквивалентности такого представителя нет. Эта дополнительная точка ведет себя как бесконечность без знака, что делает топологически такой же, как круг . Преимущество над кругом состоит в том, что некоторые геометрические объекты имеют более простые уравнения в терминах А и B. Так обстоит дело с лентой Мёбиуса.
Реализация открытой ленты Мёбиуса дается множеством
Если мы удалим строку из M (или фактически любую строку), то получившееся подмножество можно вложить в евклидово пространство . Удаление этой строки дает набор
куда м соответствует .
Существует реализация замкнутой ленты Мёбиуса в виде аналогичного множества, но с дополнительным неравенством для создания границы:
Граница N это множество всех точек с . Геометрия N очень похож на M, поэтому мы сосредоточимся на M в дальнейшем.
Геометрия M можно описать линиями, проходящими через начало координат. Каждая линия, проходящая через начало координат в - множество решений уравнения . Набор решений не меняется при изменяется масштаб, поэтому линия зависит только от класса эквивалентности . То есть линии, проходящие через начало координат, параметризованы . Кроме того, каждая точка в , кроме , лежит на единственной линии, проходящей через начало координат, в частности, на линии, определяемой . Смысл однако лежит на каждой линии, проходящей через начало координат. Для этой точки уравнение перерождается в . Это всегда правда, поэтому каждый это решение. Следовательно, множество M можно описать как несвязный союз набора линий через начало координат. Это то же самое, что и объединение линий через начало координат, за исключением того, что оно содержит по одной копии исходной точки для каждой линии. Эти дополнительные копии оригинала являются копией и составляют центральный круг ленты Мебиуса. Сами строки описывают господство ленты Мебиуса. Эта точка зрения на M показывает это как общее пространство пучок тавтологических линий на так же хорошо как Взрывать происхождения в .
Чтобы увидеть половину поворота M, начнем с точки в . Это соответствует уникальной точке M, а именно . Нарисуйте полукруг против часовой стрелки, чтобы образовался путь на M данный . Путь останавливается в , где он дает точку . Кроме п и Q, каждая точка пути лежит на отдельной прямой, проходящей через начало координат. Следовательно проходит один раз вокруг центрального круга M. Однако пока п и Q лежат в одной линии постановки, они находятся по разные стороны от начала координат. Это изменение знака - алгебраическое проявление полувручения.
Связанные объекты
Тесно связанный «странный» геометрический объект - это Бутылка Клейна. Теоретически бутылка Клейна может быть изготовлена путем склеивания двух лент Мебиуса по краям; однако это невозможно сделать в обычных трехмерных Евклидово пространство без создания самопересечений.[16]
Еще одно тесно связанное многообразие - это реальная проективная плоскость. Если круговой диск вырезать из реальной проективной плоскости, то останется лента Мёбиуса.[17] Если пойти в другом направлении, если приклеить диск к ленте Мёбиуса, указав их границы, в результате получится проективная плоскость. Чтобы визуализировать это, полезно деформировать ленту Мёбиуса так, чтобы ее граница была обычной окружностью (см. Выше). Реальная проективная плоскость, как и бутылка Клейна, не может быть встроена в трехмерное пространство без самопересечений.
В теория графов, то Лестница Мебиуса это кубический граф тесно связан с лентой Мёбиуса.
В 1968 году Гонсало Велес Ян (UCV, Каракас, Венесуэла) обнаружил трехмерные тела с мёбскими характеристиками;[18] позже они были описаны Мартин Гарднер как призматические кольца, ставшие тороидальными многогранниками в его августе 1978 г. Колонка "Математические игры" в журнале Scientific American.[19]
Приложения

Лента Мёбиуса нашла несколько технических применений. Гигантские полоски Мебиуса использовались в качестве конвейерные ленты которые служат дольше, потому что вся поверхность ленты изнашивается так же, как и ленты с непрерывной записью (чтобы удвоить время воспроизведения). Ленты Мебиуса широко используются при производстве компьютерных принтеров для ткани и ленты для пишущей машинки, поскольку они позволяют ленте быть вдвое шире печатающей головки при равномерном использовании обеих половин.[20]
А Резистор Мёбиуса представляет собой элемент электронной схемы, который нейтрализует собственное индуктивное сопротивление. Никола Тесла запатентовал аналогичную технологию в 1894 году:[21] «Катушка для электромагнитов» предназначалась для использования с его системой глобальной передачи электричества без проводов.
Лента Мебиуса - это конфигурационное пространство двух неупорядоченных точек на окружности. Следовательно, в теория музыки, пространство всех аккордов из двух нот, известное как диады, принимает форму ленты Мёбиуса; это и обобщения на большее количество пунктов является важным применение орбифолдов к теории музыки.[22][23]
В физика / электротехника как:
- Компактный резонатор с резонансной частотой, вдвое меньшей, чем у линейных катушек идентичной конструкции.[24]
- Безиндукционный резистор[25]
- Сверхпроводники с высокой температурой перехода[26]
- Резонатор Мебиуса[27]
В химия / нанотехнологии как:
- Молекулярные узлы со специальными характеристиками (узелок [2], хиральность)
- Молекулярные двигатели[28]
- Объем графена (нанографит) с новыми электронными характеристиками, такими как винтовой магнетизм[29]
- Особый вид ароматности: Ароматичность Мёбиуса
- Заряженные частицы, попавшие в магнитное поле Земли, которые могут двигаться по ленте Мебиуса.
- В циклотид (циклический белок) калата B1, действующее вещество растения Oldenlandia affinis, содержит топологию Мёбиуса для пептидного остова.
Искусство и развлечения

Принцип ленты Мёбиуса был использован как метод создания иллюзия магии. Уловка, известная как афганские банды, была очень популярна в первой половине двадцатого века. Существует множество версий этого трюка, которые применялись известными иллюзионистами, такими как Гарри Блэкстоун-старший и Томас Нельсон Даунс.[30][31]
В творческих работах
В универсальный символ утилизации (♲) три стрелки образуют петлю Мебиуса. По словам его дизайнера Гэри Андерсон, «фигура была спроектирована как лента Мебиуса, чтобы символизировать непрерывность внутри конечного объекта».[32]
Смотрите также
Рекомендации
- ^ Уэллс, Джон С. (2008). Словарь произношения Longman (3-е изд.). Лонгман. ISBN 978-1-4058-8118-0.
- ^ а б c Август Фердинанд Мёбиус, Архив истории математики MacTutor. History.mcs.st-andrews.ac.uk. Проверено 26 апреля 2017.
- ^ Клиффорд А. Пиковер (Март 2005 г.). Лента Мёбиуса: Чудесная группа доктора Августа Мёбиуса по математике, играм, литературе, искусству, технологиям и космологии. Громовой пресс. ISBN 978-1-56025-826-1.
- ^ Райнер Хергес (2004). Мёбиус, Эшер, Бах - Необычный оркестр в Kunst und Wissenschaft . В: Naturwissenschaftliche Rundschau, 58.06.2005.. С. 301–310. ISSN 0028-1050.
- ^ Крис Родли (редактор) (1997). Линч на Линче. Лондон, Бостон. п. 231.CS1 maint: дополнительный текст: список авторов (связь)
- ^ Ларисон, Лоррейн Л. (1973). «Полоса Мебиуса в римских мозаиках». Американский ученый. 61 (5): 544–547. Bibcode:1973AmSci..61..544L.
- ^ Картрайт, Джулиан Х. Э .; Гонсалес, Диего Л. (2016). «Ленты Мёбиуса перед Мёбиусом: топологические намеки на древние представления». Математический интеллект. 38 (2): 69–76. arXiv:1609.07779. Bibcode:2016arXiv160907779C. Дои:10.1007 / s00283-016-9631-8. МИСТЕР 3507121.
- ^ Андрей Николаевич Колмогоров, Юшкевич Адольф Петрович (ред.), Математика XIX века: геометрия, теория аналитических функций, Birkhäuser, 2012, стр. 101.
- ^ Старостин Е.Л .; van der Heijden G.H.M. (2007). «Форма ленты Мёбиуса». Материалы Природы. 6 (8): 563–7. Дои:10.1038 / nmat1929. PMID 17632519.
- ^ Барр, Стивен (1964). Эксперименты в топологии. Нью-Йорк: Компания Томаса И. Кроуэлла. стр.48, 200–201.
- ^ Дмитрий Фукс и Серж Табачников, Математический омнибус: тридцать лекций по классической математике, 2007, стр. 199, на http://www.math.psu.edu/tabachni/Books/taba.pdf В архиве 2016-04-24 в Wayback Machine
- ^ Тони Филлипс, Взгляд Тони Филлипса на математику в СМИ, Американское математическое общество, Октябрь 2006 г.
- ^ Паркер, Филлип (1993). «Пространства геодезии». Aportaciones Matemáticas. Notas de Investigación: 67–79.
- ^ Гильберт, Дэвид; Кон-Фоссен, Стефан (1952). Геометрия и воображение (2-е изд.). Челси. ISBN 978-0-8284-1087-8.
- ^ Дэн Азимов; Дуг Лернер (1984). «Выпуск 17 Электронный театр SIGGRAPH '84».
- ^ Спивак, Майкл (1979). Комплексное введение в дифференциальную геометрию, том I (2-е изд.). Уилмингтон, Делавэр: опубликовать или погибнуть. п. 591.
- ^ Гильберт, Дэвид; Кон-Фоссен, С. (1999). Геометрия и воображение (2-е изд.). Провиденс, Род-Айленд: Американское математическое общество. п. 316. ISBN 978-0-8218-1998-2.
- ^ Демонстрационный проект Вольфрама: Тороидальный многогранник Мебиуса Велес-Яна
- ^ Это был третий раз, когда Гарднер представил ленту Мёбиуса в своей колонке.
- ^ Хогарт, Ян В. и Кевнинг, Фридхельм. (1991) "Пишущая машинка или лента для принтера и способ ее изготовления" Патент США 5,062,725
- ^ Тесла, Никола (1894) "Катушка для электромагнитов" Патент США 512,340
- ^ Клара Московиц, Музыка, сведенная к красивой математике, LiveScience
- ^ Дмитрий Тимочко (7 июля 2006 г.). «Геометрия музыкальных аккордов». Наука. 313 (5783): 72–4. Bibcode:2006Научный ... 313 ... 72Т. CiteSeerX 10.1.1.215.7449. Дои:10.1126 / science.1126287. PMID 16825563.
- ^ Понд, Дж. М. (2000). «Двухмодовые резонаторы Мебиуса и полосовые фильтры». Протоколы IEEE по теории и методам микроволнового излучения. 48 (12): 2465–2471. Bibcode:2000ITMTT..48.2465P. Дои:10.1109/22.898999.
- ^ Дэвис, Ричард Л. (1966) "Неиндуктивный электрический резистор" Патент США 3267406
- ^ Энрикес, Рауль Перес (2002). «Структурный параметр для высокотемпературной сверхпроводимости из октаэдрической ленты Мебиуса в перовските типа RBaCuO: 123». Rev Mex Fis. 48 (приложение 1): 262. arXiv:cond-mat / 0308019. Bibcode:2003 второй мат..8019P.
- ^ «Печатные резонаторы: теория ленты Мебиуса и приложения» (PDF). Микроволновый журнал. 56 (11). Ноябрь 2013.
- ^ Лукин, О; Фогтле, Ф (2005). «Узлы и нитки молекул: химия и хиральность молекулярных узлов и их сборок». Angewandte Chemie International Edition. 44 (10): 1456–77. Дои:10.1002 / anie.200460312. PMID 15704147.
- ^ Ямасиро, Ацуши; Шимои, Юкихиро; Харигая, Кикуо; Вакабаяси, Кацунори (2004). «Новые электронные состояния в графеновых лентах - Конкурирующие порядки вращения и заряда». Physica E. 22 (1–3): 688–691. arXiv:cond-mat / 0309636. Bibcode:2004PhyE ... 22..688Y. Дои:10.1016 / j.physe.2003.12.100.
- ^ Превос, Питер (2018). Лента Мебиуса в магии: трактат об афганских бандах. Кенгуру-квартира: третье полушарие.
- ^ Гарднер, Мартин (1956). Математика, магия и тайна. Нью-Йорк: Dover Books. С. 70–73.
- ^ Джонс, Пенни; Джерри Пауэлл (май 1999 г.). «Гэри Андерсон найден!» (PDF). Переработка ресурсов: журнал по переработке и компостированию Северной Америки: стр.1–2. Получено 2011-05-26.











![{ Displaystyle [0,1] раз [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/92f35a051af39d8299688d7c4a63e39ee5f95c8b)









![{ displaystyle [A: B] = {( lambda A, lambda B): lambda in mathbf {R} setminus {0 } }.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1703ee596b1a95aff033e95cb094f748509b4960)
![{ displaystyle [A: B]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/33dede24122dab634ef6f1bd8655cfed1922ce0a)



![{ displaystyle [1: 0]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2c9d83f60abcf946cc50d3cb984fecd2df57977b)

![{ displaystyle M = {((x, y), [A: B]) in mathbf {R} ^ {2} times mathbf {RP} ^ {1}: Ax = By }.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0b404d0e84ae1eda5eab105bc8e3922a87937efc)


![{ Displaystyle { begin {align} M '& = {((x, y), [A: B]) in mathbf {R} ^ {2} times mathbf {RP} ^ {1} : Ax = By, B neq 0 } & = {(x, y, m) in mathbf {R} ^ {3}: mx = y }, end {align}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bcf3b7938d9e36db364fc7a559a516d0e9a9cb9c)

![{ Displaystyle N = {((x, y), [A: B]) in mathbf {R} ^ {2} times mathbf {RP} ^ {1}: Ax = By, x ^ {2} + y ^ {2} leq 1 }.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c6b2f6cc02685f04099ed246d0abef0d90983481)






![{ displaystyle [-y: x]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/86fd60d8c2287388ac6c39f3768881a5b1791661)





![{ Displaystyle P = ((1,0), [0: 1])}](https://wikimedia.org/api/rest_v1/media/math/render/svg/82494e67b7475f512a85350bff1a409dbfff6e3e)
![{ Displaystyle гамма (T) = (( соз (2 пи т), грех (2 пи т)), [- грех (2 пи т), соз (2 пи т)] )}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8e4fca428e81158af73db9be51c049bcaae2550c)

![{ Displaystyle Q = ((- 1,0), [0: 1])}](https://wikimedia.org/api/rest_v1/media/math/render/svg/70844f757d63a3ab25862cb0d874d64120901951)
