Четвертая проблема Гильберта - Hilberts fourth problem

В математика, Четвертая проблема Гильберта в 1900 году Проблемы Гильберта это фундаментальный вопрос в геометрия. В одном утверждении, заимствованном из оригинала, было найдено - с точностью до изоморфизма - все геометрии которые имеют аксиоматический система классической геометрии (Евклидово, гиперболический и эллиптический ), с этими аксиомами соответствие которые связаны с понятием опущенного угла, и `неравенство треугольника - добавлено, как аксиома.

Если дополнительно принять аксиому непрерывности, то в случае евклидовой плоскости мы приходим к проблеме, поставленной Дарбу: «Определить все вариационные задачи на плоскости, решениями которых являются все плоские прямые».^[1]

Есть несколько интерпретаций первоначального утверждения Гильберта. Тем не менее решение было найдено у немецкого математика. Георг Хамель быть первым, кто внес свой вклад в решение четвертой проблемы Гильберта.^[2]

Признанное решение дал украинский математик. Алексей Погорелов в 1973 г.^[3][4] В 1976 году армянский математик Рубен В. Амбарцумян предложил другое доказательство четвертой проблемы Гильберта.^[5]

Оригинальное заявление

Гильберт обсуждает существование неевклидова геометрия и неархимедова геометрия

... геометрия, в которой выполняются все аксиомы обычной евклидовой геометрии, и, в частности, все аксиомы сравнения, кроме аксиомы сравнения треугольников (или всех, кроме теоремы о равенстве углов основания в равнобедренном треугольнике), и в котором, кроме того, утверждение о том, что в каждом треугольнике сумма двух сторон больше третьей, принимается как особая аксиома.^[6]

Из-за идеи, что «прямая линия» определяется как кратчайший путь между двумя точками, он упоминает, как согласованность треугольников необходима для доказательства Евклида, что прямая линия на плоскости - это кратчайшее расстояние между двумя точками. Он резюмирует следующее:

Теорема о прямой как о кратчайшем расстоянии между двумя точками и эквивалентная теорема Евклида о сторонах треугольника играют важную роль не только в теории чисел, но также в теории поверхностей и в вариационном исчислении. По этой причине и потому, что я считаю, что тщательное исследование условий справедливости этой теоремы прольет новый свет на идею расстояния, а также на другие элементарные идеи, например. g., исходя из идеи плоскости и возможности ее определения с помощью идеи прямой линии, мне кажется желательным построение и систематическая обработка геометрических форм здесь возможных.^[6]

Плоские метрики

Теорема дезарга

Теорема дезарга:

Если два треугольника лежат на плоскости так, что прямые, соединяющие соответствующие вершины треугольников, пересекаются в одной точке, то три точки, в которых пересекаются продолжения трех пар соответствующих сторон треугольников, лежат на одной прямой.

Необходимым условием для решения четвертой проблемы Гильберта является требование, чтобы метрическое пространство, удовлетворяющее аксиомам этой проблемы, было дезарговским, т. Е.:

• если пространство имеет размерность 2, то теорема Дезарга и обратная к ней должны выполняться;
• если пространство имеет размерность больше 2, то любые три точки должны лежать на одной плоскости.

Для дезарговских пространств Георг Хамель доказал, что каждое решение четвертой проблемы Гильберта может быть представлено в виде проективное пространство ${\displaystyle RP^{n}}$ или в выпуклой области ${\displaystyle RP^{n}}$ если определить конгруэнтность отрезков равенством их длин в специальной метрике, для которой линии проективного пространства являются геодезическими.

Метрики этого типа называются плоский или же проективный.

Таким образом, решение четвертой проблемы Гильберта свелось к решению проблемы конструктивного определения всех полных плоских метрик.

Гамель решил эту проблему в предположении высокой регулярности метрики.^[2] Однако, как показывают простые примеры, класс обычных плоских метрик меньше, чем класс всех плоских метрик. Рассматриваемые аксиомы геометрий подразумевают только непрерывность метрики. Следовательно, для полного решения четвертой проблемы Гильберта необходимо конструктивно определить все непрерывные плоские метрики.

Предыстория четвертой проблемы Гильберта

Модель Кэли – Клейна геометрии Лобачевского

До 1900 г. Модель Кэли-Клейна геометрии Лобачевского в единичном круге, согласно которой геодезические линии являются хордами диска, а расстояние между точками определяется как логарифм перекрестное соотношение четверки. Для двумерных римановых метрик Эухенио Бельтрами (1835–1900) доказал, что плоские метрики - это метрики постоянной кривизны.^[7]

Для многомерных римановых метрик это утверждение было доказано Э. Картан в 1930 г.

В 1890 г. для решения задач теории чисел Герман Минковски ввел понятие пространства, которое сегодня называется конечномерным Банахово пространство.^[8]

Пространство Минковского

Основная статья: Пространство Минковского

Пространство Минковского

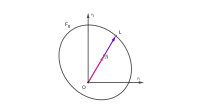
Позволять ${\displaystyle F_{0}\subset \mathbb {E} ^{n}}$- компактная выпуклая гиперповерхность в евклидовом пространстве, определяемая формулой

${\displaystyle F_{0}=\{y\in E^{n}:F(y)=1\},}$

где функция ${\displaystyle F=F(y)}$ удовлетворяет следующим условиям:

1. ${\displaystyle F(y)\geqslant 0,\qquad F(y)=0\Leftrightarrow y=0;}$
2. ${\displaystyle F(\lambda y)=\lambda F(y),\qquad \lambda \geqslant 0;}$
3. ${\displaystyle F(y)\in C^{k}(E^{n}\setminus \{0\}),\qquad k\geqslant 3;}$
4. и форма ${\displaystyle {\frac {\partial ^{2}F^{2}}{\partial y^{i}\,\partial y^{j}}}\xi ^{i}\xi ^{j}>0}$ положительно определен.

Длина вектора OA определяется:

${\displaystyle \|OA\|_{M}={\frac {\|OA\|_{\mathbb {E} }}{\|OL\|_{\mathbb {E} }}}.}$

Пространство с этой метрикой называется Пространство Минковского.

Гиперповерхность ${\displaystyle F_{0}}$ выпуклая и может быть неправильной. Определенная метрика плоская.

Финслеровы пространства

Основная статья: Метрика Финслера

Позволять M и ${\displaystyle TM=\{(x,y)|x\in M,y\in T_{x}M\}}$ - гладкое конечномерное многообразие и его касательное расслоение соответственно. Функция ${\displaystyle F(x,y)\colon TM\rightarrow [0,+\infty )}$ называется Метрика Финслера если

1. ${\displaystyle F(x,y)\in C^{k}(TM\setminus \{0\}),\qquad k\geqslant 3}$;
2. Для любой точки ${\displaystyle x\in M}$ ограничение ${\displaystyle F(x,y)}$ на ${\displaystyle T_{x}M}$ - норма Минковского.

${\displaystyle (M,F)}$ является Финслеровское пространство.

Геометрия Гильберта

Метрика Гильберта

Позволять ${\displaystyle U\subset (\mathbb {E} ^{n+1},\|.\|_{\mathbb {E} })}$ - ограниченное открытое выпуклое множество с границей класса C² и положительные нормальные искривления. Аналогично пространству Лобачевского гиперповерхность ${\displaystyle \partial U}$ называется абсолютом геометрии Гильберта.^[9]

Расстояние Гильберта (см. Рис.) Определяется как

${\displaystyle d_{U}(p,q)={\frac {1}{2}}\ln {\frac {\|q-q_{1}\|_{E}}{\|q-p_{1}\|_{E}}}\times {\frac {\|p-p_{1}\|_{E}}{\|p-q_{1}\|_{E}}}.}$

Метрика Гильберта – Финслера

Расстояние ${\displaystyle d_{U}}$ побуждает Метрика Гильберта – Финслера ${\displaystyle F_{U}}$ на U. Для любого ${\displaystyle x\in U}$ и ${\displaystyle y\in T_{x}U}$ (см. рис.), имеем

${\displaystyle F_{U}(x,y)={\frac {1}{2}}\|y\|_{\mathbb {E} }\left({\frac {1}{\|x-x_{+}\|_{\mathbb {E} }}}+{\frac {1}{\|x-x_{-}\|_{\mathbb {E} }}}\right).}$

Метрика симметричная и плоская. В 1895 году Гильберт ввел эту метрику как обобщение геометрии Лобачевского. Если гиперповерхность ${\displaystyle \partial U}$ эллипсоид, то имеем геометрию Лобачевского.

Метрика фанка

В 1930 году Функ ввел несимметричную метрику. Он определен в области, ограниченной выпуклой замкнутой гиперповерхностью, и также является плоской.

σ-метрики

Достаточное условие для плоских метрик

Георг Хамель был первым, кто внес свой вклад в решение четвертой проблемы Гильберта.^[2] Он доказал следующее утверждение.

Теорема. Обычная финслерова метрика ${\displaystyle F(x,y)=F(x_{1},\ldots ,x_{n},y_{1},\ldots ,y_{n})}$ плоский тогда и только тогда, когда он удовлетворяет условиям:

${\displaystyle {\frac {\partial ^{2}F^{2}}{\partial x^{i}\,\partial y^{j}}}={\frac {\partial ^{2}F^{2}}{\partial x^{j}\,\partial y^{i}}},\,i,j=1,\ldots ,n.}$

Формула Крофтона

Основная статья: Формула Крофтона

Рассмотрим набор всех ориентированных прямых на плоскости. Каждая строка определяется параметрами ${\displaystyle \rho }$ и ${\displaystyle \varphi ,}$ куда${\displaystyle \rho }$ расстояние от начала координат до линии, а ${\displaystyle \varphi }$ угол между линией и Икс-ось. Тогда множество всех ориентированных прямых гомеоморфно круговому цилиндру радиуса 1 с элементом площади ${\displaystyle dS=d\rho \,d\varphi }$. Позволять ${\displaystyle \gamma }$ - спрямляемая кривая на плоскости. Тогда длина ${\displaystyle \gamma }$ является

${\displaystyle L={\frac {1}{4}}\iint \limits _{\Omega }n(\rho ,\varphi )\,dp\,d\varphi }$

куда ${\displaystyle \Omega }$ набор линий, пересекающих кривую ${\displaystyle \gamma }$, и ${\displaystyle n(p,\varphi )}$ - количество пересечений прямой с $ gamma $. Крофтон доказал это утверждение в 1870 году.^[10]

Аналогичное утверждение верно для проективного пространства.

Мера Бляшке – Буземана

В 1966 году в своем выступлении на Международный математический конгресс в Москве, Герберт Буземанн представил новый класс плоских показателей. На множестве прямых на проективной плоскости ${\displaystyle RP^{2}}$ он ввел полностью аддитивную неотрицательную меру ${\displaystyle \sigma }$, который удовлетворяет следующим условиям:

1. ${\displaystyle \sigma (\tau P)=0}$, куда ${\displaystyle \tau P}$ представляет собой набор прямых, проходящих через точку п;
2. ${\displaystyle \sigma (\tau X)>0}$, куда ${\displaystyle \tau X}$ это набор прямых, проходящих через некоторое множество Икс содержащий отрезок прямой;
3. ${\displaystyle \sigma (RP^{n})}$ конечно.

Если мы рассмотрим ${\displaystyle \sigma }$-метрика в произвольной выпуклой области ${\displaystyle \Omega }$ проективного пространства ${\displaystyle RP^{2}}$, то условие 3) следует заменить на следующее: для любого множества ЧАС такой, что ЧАС содержится в ${\displaystyle \Omega }$ и закрытие ЧАС не пересекает границу ${\displaystyle \Omega }$, неравенство

${\displaystyle \sigma (\pi H)<\infty }$ держит.^[11]

Используя эту меру, ${\displaystyle \sigma }$-метрика на ${\displaystyle RP^{2}}$ определяется

${\displaystyle |x,y|=\sigma \left(\tau [x,y]\right),}$

куда ${\displaystyle \tau [x,y]}$ набор прямых, пересекающих отрезок ${\displaystyle [x,y]}$.

Неравенство треугольника для этой метрики следует из Теорема Паша.

Теорема. ${\displaystyle \sigma }$-метрика на ${\displaystyle RP^{2}}$ является плоским, т.е. геодезические - это прямые проективного пространства.

Но Буземан был далек от мысли, что ${\displaystyle \sigma }$-метрики исчерпывают все плоские метрики. Он написал, «Свобода выбора метрики с заданными геодезическими для неримановых метрик настолько велика, что можно усомниться в том, действительно ли существует убедительная характеризация всех дезарговых пространств».^[11]

Двумерный корпус

Теорема Погорелова

Следующая замечательная теорема была доказана Погореловым в 1973 г.^[3][4]

Теорема. Любая двумерная непрерывная полная плоская метрика является ${\displaystyle \sigma }$-метрический.

Таким образом, четвертая проблема Гильберта для двумерного случая была полностью решена.

Доказательства Амбарцумяна

В 1976 г. Амбарцумян предложил еще одно доказательство четвертой проблемы Гильберта.^[5]

Его доказательство использует тот факт, что в двумерном случае вся мера может быть восстановлена ​​по ее значениям на двуугольниках и, таким образом, может быть определена на треугольниках так же, как площадь треугольника определяется на сфере. Поскольку выполнено неравенство треугольника, эта мера положительна на невырожденных треугольниках и определена на всех Наборы Бореля. Однако эта структура не может быть обобщена на более высокие измерения из-за третьей проблемы Гильберта, решенной с помощью Макс Ден.

В двумерном случае многоугольники с одинаковым объемом равны ножницам. Как показал Ден, это неверно для более высокого измерения.

Трехмерный корпус

Для трехмерного случая Погорелов доказал следующую теорему.

Теорема. Любая трехмерная регулярная полная плоская метрика является ${\displaystyle \sigma }$-метрический.

Однако в трехмерном случае ${\displaystyle \sigma }$-меры могут принимать как положительные, так и отрицательные значения. Необходимые и достаточные условия регулярной метрики, определяемой функцией множества ${\displaystyle \sigma }$ Чтобы быть плоским, выполняются следующие три условия:

1. Значение ${\displaystyle \sigma }$ на любой плоскости равно нулю,
2. Значение ${\displaystyle \sigma }$ в любом конусе неотрицательна,
3. Значение ${\displaystyle \sigma }$ положительна, если конус содержит внутренние точки.

Более того, Погорелов показал, что всякая полная непрерывная плоская метрика в трехмерном случае является пределом регулярных ${\displaystyle \sigma }$-метрики с равномерной сходимостью на любой компактной подобласти области определения метрики. Он назвал их обобщенными ${\displaystyle \sigma }$-метрики.

Таким образом, Погорелов смог доказать следующее утверждение.

Теорема. В трехмерном случае любая полная непрерывная плоская метрика является ${\displaystyle \sigma }$-метрический в обобщенном смысле.

Буземан в своей рецензии на книгу Погорелова «Четвертая проблема Гильберта» писал: «В духе времени Гильберт ограничился п = 2, 3 То же самое и с Погореловым. Однако это, несомненно, имеет педагогические причины, поскольку он адресован широкому кругу читателей. Настоящая разница между п = 2 и п> 2. Метод Погорелова работает для п> 3, но требует более подробного описания ".^[12]

Многомерный случай

Многомерный случай Четвертой проблемы Гильберта изучал Сабо.^[13] В 1986 году он доказал, как он писал, обобщенную теорему Погорелова.

Теорема. Каждый п-мерное дезаргово пространство класса ${\displaystyle C^{n+2},n>2}$, порождается конструкцией Бляшке – Буземана.

А ${\displaystyle \sigma }$-мера, которая генерирует плоскую меру, имеет следующие свойства:

1. то ${\displaystyle \sigma }$- размер гиперплоскостей, проходящих через неподвижную точку, равен нулю;
2. то ${\displaystyle \sigma }$-меры множества гиперплоскостей, пересекающих два отрезка [Икс, у], [у, z], куда Икс, у та z не коллинеарны, положительна.

Приведен пример плоской метрики, не порождаемой конструкцией Бляшке – Буземана. Сабо описал все непрерывные плоские метрики в терминах обобщенных функций.

Четвертая проблема Гильберта и выпуклые тела

Четвертая проблема Гильберта также тесно связана со свойствами выпуклые тела. Выпуклый многогранник называется зонотоп если это Сумма Минковского сегментов. Выпуклое тело, являющееся пределом зонотопов в метрике Бляшке - Хаусдорфа, называется зоноид. Для зоноидов функция поддержки представлен

${\displaystyle h(x)=\int \limits _{S^{n-1}}|\langle x,u\rangle |\,\partial \sigma (u),\qquad (1)}$

куда ${\displaystyle \sigma (u)}$ даже положительный Мера Бореля на сфере ${\displaystyle S^{n-1}}$.

Пространство Минковского порождается конструкцией Бляшке – Буземана тогда и только тогда, когда опорная функция индикатрисы имеет вид (1), где ${\displaystyle \sigma (u)}$ четная и не обязательно положительной борелевской меры.^[14] Тела, ограниченные такими гиперповерхностями, называются генерализованные зоноиды.

Октаэдр ${\displaystyle |x_{1}|+|x_{2}|+|x_{3}|\leqslant 1}$ в евклидовом пространстве ${\displaystyle E^{3}}$ не является обобщенным зоноидом. Из приведенного выше утверждения следует, что плоская метрика пространства Минковского с нормой ${\displaystyle \|x\|=\max\{|x_{1}|,|x_{2}|,|x_{3}|\}}$ не порождается конструкцией Бляшке – Буземана.

Обобщения четвертой проблемы Гильберта.

Обнаружено соответствие между планарными п-мерные финслеровы метрики и специальные симплектические формы на грассмановом многообразии ${\displaystyle G(n+1,2)}$ в ${\displaystyle E^{n+1}}$.^[15]

Были рассмотрены периодические решения четвертой проблемы Гильберта:

1) Пусть (M, грамм) - компактное локально евклидово риманово многообразие. Предположим, что ${\displaystyle C^{2}}$ Метрика Финслера на M с теми же геодезическими, что и в метрике грамм дано. Тогда финслерова метрика является суммой локально метрики Минковского и замкнутой 1-формы.^[16]

2) Пусть (М, г) - компактное симметрическое риманово пространство ранга больше единицы. Если F симметричный ${\displaystyle C^{2}}$ Финслерова метрика, геодезические которой совпадают с геодезическими римановой метрики грамм, тогда (М, г) является симметричным финслеровым пространством.^[16] Аналог этой теоремы для симметрических пространств ранга один пока не доказан.

Еще одно изложение четвертой проблемы Хильбетта можно найти в работе Пайвы.^[17]

Нерешенные проблемы

1. Четвертая проблема Хильбетта для несимметричной финслеровой метрики до сих пор не решена.
2. Описание метрики на ${\displaystyle RP^{n}}$ для которого k-самолеты минимизируют k- площадь не указана (Буземанн).^[18]

Рекомендации

1. Г. Дарбу, Lecons sur la theorie generale des поверхностей, V.III, Париж, 1894 г.
2. Г. Хамель, Uber die Geometrien in denen die Geraden die Kurzesten sind, Математика. Анна. 57 (1903), 221–264.
3. А. В. Погорелов, Полное решение IV проблемы Гильберта, ДАН СССР № 208, т.1 (1973), 46–49. Английский перевод: A.V. Погорелов, Полное решение четвертой проблемы Гильберта, Докл. Акад. Наук ССР, Т. 208, № 1 (1973), 48–52.
4. А. В. Погорелов, Четвертая Проблема Гильберта. Наука, 1974. Английский перевод: А.В. Погорелов, Четвертая проблема Гильберта, Scripta Series in Mathematics, Winston and Sons, 1979.
5. Р. В. Амбарцумян, Заметка о псевдометриках на плоскости, Zeitschrift für Wahrscheinlichkeitstheorie und Verwandte Gebiete, 1976, Том 37, Выпуск 2, стр 145–155
6. Гильберт, Дэвид, "Mathematische Probleme" Göttinger Nachrichten, (1900), pp. 253–297, и в Archiv der Mathematik und Physik, (3) 1 (1901), 44–63 и 213–237. Опубликовано в английском переводе доктора Маби Винтон Ньюсон, Бюллетень Американского математического общества 8 (1902), 437–479 [1] [2] Дои:10.1090 / S0002-9904-1902-00923-3. [Более полное название журнала Göttinger Nachrichten - Nachrichten von der Königl. Gesellschaft der Wiss. zu Göttingen.]
7. Э. Бельтрами, Рисунок проблемы: Riportare i punti di una superficie sobra un piano in modo che le linee geodetiche Vengano rappresentate da linee rette, Annali di Matematica Pura ed Applicata, № 7 (1865), 185–204.
8. Х. Минковский, Geometrie der Zahlen, Лпз.-Б., 1953.
9. Д. Гильберт, Uber die gerade Linie как kurzeste Verbindung zweier Punkte, Математика. Ann., 46 (1895), 91-96.
10. Сантало Л. А. Интегральная геометрия. В: Исследования в области глобальной геометрии и анализа (С.С. Черн, ред.), Вашингтон, округ Колумбия: Математика. Asoc. Амер, 147–195.
11. Х. Буземан, Геометрия геодезии, Нью-Йорк, Academic Press, 1955.
12. Х. Буземанн, Рецензия на: Погорелов А.В., Четвертая проблема Гильберта., Бык. Амер. Математика. Soc. (Н.С.) Т. 4, № 1 (1981), 87-90.
13. З. И. Сабо, Четвертая проблема Гильберта I, Adv. Математика. 59 (1986), 185–301.
14. Р. Александр, Теория зоноидов и четвертая проблема Гильберта, Геом. Дедиката 28, № 2 (1988), 199–211.
15. Дж. К. Альварес Пайва, Симплетическая геометрия и четвертая проблема Гильберта, J. Differ. Геом. 69, № 2 (2005), 353–378.
16. Х. К. Альварес Павиа и Х. Барбоса Гомеш, Периодические решения четвертой проблемы Гильберта., 20 с. ArXiv: 1809.02783v1 [math.MG], 2018.
17. Пайва, Х.С. Альварес. «Четвертая проблема Гильберта в двух измерениях». MASS selecta (2003): 165–183.
18. А. Пападопулос, О четвертой проблеме Гильберта, 1–43. Справочник по геометрии Гильберта (ред. А. Пападопулос и М. Троянов), Европейское математическое общество, Лекции ИРМА по математике и теоретической физике, № 22 (2014), с. 460.

дальнейшее чтение

• Буземанн, Герберт (1976). «Проблема IV. Дезарговы пространства». В Браудер, Феликс Э. (ред.). Математические разработки, возникающие из проблем Гильберта. Труды симпозиумов по чистой математике. XXVIII. Американское математическое общество. С. 131–141. ISBN  0-8218-1428-1. Zbl  0352.50010.
• Пападопулос, Афанас (2014). «Четвертая проблема Гильберта». Справочник по геометрии Гильберта (под ред. А. Пападопулоса и М. Троянова).. Лекции ИРМА по математике и теоретической физике. 22. Европейское математическое общество. С. 391–432. ISBN  978-3-03719-147-7.