Круг пятых - Circle of fifths

Пятый круг, показывающий мажор и минор

Николай Дилецкий пятый круг в Идея грамматики музыкальной (Москва, 1679 г.)

В теория музыки, то цикл или же круг пятых (или же круг четвертых) - это отношение между 12 тонами (или поля ) из хроматическая шкала, соответствующие им ключевые подписи, и связанные основные и второстепенные ключи. В частности, это геометрический представление отношений между 12 классы поля хроматической гаммы в пространство питч-класса.

Определение

Период, термин "пятый "определяет интервал или математическое соотношение, которое является ближайшим и наиболее согласный звук неоктавный интервал. Круг квинт - это последовательность высот или ключевых тональностей, представленная в виде круга, в котором следующий шаг (поворот по часовой стрелке) находится на семи полутоны выше, чем последний. Музыкантов и композиторы используйте круг квинт, чтобы понять и описать музыкальные отношения между некоторыми выбранными этими тонами. Дизайн круга полезен в составление и гармонизирующий мелодии, строительство аккорды, и модулируя на разные ключи в составе.^[1]

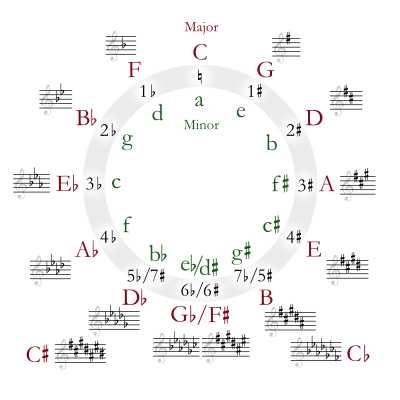
В верхней части круга значок ключ до мажор не имеет острые предметы или же квартиры. Начиная с вершины и продолжая по часовой стрелке по восходящей пятые, тональность G имеет один диез, тональность D - 2 диеза и так далее. Точно так же, двигаясь против часовой стрелки от вершины по нисходящей пятой части, тональность F имеет одну плоскость, тональность B♭ есть 2 квартиры и тд. Внизу круга острые и плоские клавиши перекрываются, показывая пары клавиш. энгармонически эквивалентный ключевые подписи.

Начиная с любого подача, восходящий по интервал из равноправный пятый, каждый передает все двенадцать тонов по часовой стрелке, чтобы вернуться к начальному классу высоты звука. Чтобы пройти двенадцать тонов против часовой стрелки, необходимо подняться на идеальные четверти, а не пятые. (На слух последовательность четвертей производит впечатление стабилизации или разрешения; см. каденция.)

• 

  Играть по кругу квинт по часовой стрелке в пределах одной октавы 

• 

  Играть круг квинт против часовой стрелки в пределах одной октавы 

Структура и использование

Высота тона в хроматической шкале связана не только количеством полутонов между ними в хроматической шкале, но также гармонично связана в пределах круга квинт. При движении против часовой стрелки направление пятого круга дает круг четвертых. Обычно «круг квинтов» используется при анализе классической музыки, тогда как «круг квинтов» используется при анализе джазовой музыки, но это различие не является исключительным. «Пятый круг» - требование стиля парикмахерской, поскольку Барбершоп Harmony Society В «Справочнике конкурса и судейства» говорится, что стиль парикмахерской состоит из «септаккордов, которые часто разрешаются по кругу квинт, а также используются другие разрешения», среди прочих требований.

Диатонические ключевые подписи

Круг обычно используется для обозначения отношений между диатонические гаммы. Здесь буквы в круге обозначают основную гамму с этой нотой как тонической. Цифры внутри круга показывают, сколько острых или плоских подпись ключа для этого масштаба есть. Таким образом, мажорная гамма, построенная на ля, имеет ключевую сигнатуру 3 диеза. Большая шкала, построенная на F, имеет 1 квартиру.

За минорные гаммы, поверните буквы против часовой стрелки на 3, чтобы, например, в ля минор было 0 диезов или бемолей, а в ми минор - 1 диез. (Видеть относительный ключ для подробностей.) Это явление можно описать следующим образом: для любого основного ключа [например, Соль мажор, с одним диезом (F♯) в его диатонической шкале], шкалу можно построить, начиная с шестой (VI) степени (относительный минорный тон, в данном случае, E), содержащую те же ноты, но с E – E, а не с G – G. Или, гамма G-мажор (G – A – B – C – D – E – F♯–G) энгармоничен (гармонически эквивалентен) гамме ми минор (E – F♯–G – A – B – C – D – E).

При записи ключевых подписей порядок диезов, которые находятся в начале линии нотоносца, следует по кругу квинт от F до B. Порядок - F, C, G, D, A, E, B. только один диез, например, в тональности соль мажор, затем один диез становится фа-диез. Если есть две диезы, это две F и C, и они появляются в этом порядке в ключевой подписи. Порядок диезов идет по часовой стрелке по кругу квинт. (В мажорных тональностях последний диез находится на седьмой ступени шкалы. Тоника (ключевая нота) на полшага выше последнего диеза.)

Для обозначения квартир порядок обратный: B, E, A, D, G, C, F. Этот порядок проходит против часовой стрелки по кругу квинт; другими словами, они прогрессируют на четверть. Следуя за мажорными клавишами от тональности F до тональности C-бемоль (B) против часовой стрелки по кругу пятых, поскольку каждая подпись ключа добавляет бемоль, бемоль всегда располагаются в этом порядке. (Для мажорных клавиш предпоследний (предпоследний) бемоль в ключевой сигнатуре находится на тонике. При наличии только одного бемоля тоника F не следует этому шаблону.)

Модуляция и последовательность аккордов

Тональная музыка довольно часто модулирует перемещаясь между соседними шкалами по кругу квинт. Это связано с тем, что диатонические гаммы содержат семь классов высоты звука, которые примыкают к окружности квинт. Отсюда следует, что диатонические гаммы, разделенные идеальной пятой частью, разделяют шесть из семи своих нот. Кроме того, ноты, не содержащиеся вместе, отличаются только на полтона. Таким образом, модуляция совершенной пятой части может выполняться исключительно плавно. Например, чтобы перейти от мажорной гаммы C F – C – G – D – A – E – B к мажорной гамме G C – G – D – A – E – B – F♯, нужно только переместить "F" в "F"♯".

Круг можно легко использовать для определения общей последовательности аккордов для основных клавиш. Пятый круг показывает каждую мажорную тональность с соответствующей ей минорной тональностью (эолийского режима). Его можно использовать как аккорд vi в прогрессии. Аккорды V и IV можно найти, двигаясь по часовой стрелке и против часовой стрелки от основной хорды соответственно. Соответствующие минорные клавиши V и IV - это iii и ii соответственно.

Мажорные и минорные аккорды в каждой мажорной тональности:

Аккорд Ключ	я	ii	iii	IV	V	vi
До мажор	C	Дм	Эм	F	грамм	Являюсь
Соль мажор	грамм	Являюсь	Bm	C	D	Эм
Ре мажор	D	Эм	F♯м	грамм	А	Bm
Главный	А	Bm	C♯м	D	E	F♯м
Ми мажор	E	F♯м	грамм♯м	А	B	C♯м
Си мажор	B	C♯м	D♯м	E	F♯	грамм♯м
F♯ основной	F♯	грамм♯м	А♯м	B	C♯	D♯м
C♯ основной	C♯	D♯м	E♯м	F♯	грамм♯	А♯м
C♭ основной	C♭	D♭м	E♭м	F♭	грамм♭	А♭м
грамм♭ основной	грамм♭	А♭м	B♭м	C♭	D♭	E♭м
D♭ основной	D♭	E♭м	FM	грамм♭	А♭	B♭м
А♭ основной	А♭	B♭м	См	D♭	E♭	FM
E♭ основной	E♭	FM	Gm	А♭	B♭	См
B♭ основной	B♭	См	Дм	E♭	F	Gm
Фа мажор	F	Gm	Являюсь	B♭	C	Дм

В западной тональной музыке также можно найти аккорды между аккордами, корни которых связаны идеальной пятой. Например, распространены корневые прогрессии, такие как D – G – C. По этой причине круг квинт часто используется для обозначения «гармонического расстояния» между аккордами.

IV – V – I, в C Играть в 

По мнению теоретиков, в том числе Goldman, гармоническая функция (использование, роль и отношение аккорды в гармония ), включая «функциональную преемственность», можно «объяснить кругом пятых» (в котором, следовательно, шкала степени II ближе к доминирующий чем шкала IV степени) ».^[2] С этой точки зрения тоник считается концом линии, по которой аккордная прогрессия полученный из круга квинтов прогрессирует.

ii – V – I прогрессия, в C Играйте субдоминанты, супертонические септаккорды и супертонические аккорды.  иллюстрируя сходство между ними.

По данным Goldman Гармония в западной музыке"IV аккорд фактически находится в простейших механизмах диатонических отношений на наибольшем расстоянии от I. В терминах [нисходящего] круга квинт он ведет от I, а не к нему".^[3] Таким образом, прогрессия I – ii – V – I (an подлинная каденция ) будет казаться более окончательным или решено чем I – IV – I (a чумовая каденция ). Goldman^[4] соглашается с Наттизом, который утверждает, что «аккорд четвертой степени появляется задолго до аккорда II и последующего финала I в прогрессии I – IV – vii.^о–Iii – vi – ii – V – I », и там тоже дальше от тоники.^[5] (В этой и связанных статьях римские цифры в верхнем регистре обозначают основные трезвучия, а римские цифры в нижнем регистре - второстепенные трезвучия.)

IV против II⁷ с корнем в скобках, в C Играть в .

Гольдман утверждает, что «исторически использование аккорда IV в гармоническом дизайне, и особенно в каденции, демонстрирует некоторые любопытные особенности. В целом, можно сказать, что использование IV в заключительных каденциях становится более распространенным в девятнадцатом веке, чем в восемнадцатом, но что его также можно понимать как замену аккорда II, когда он предшествует V. также вполне логично истолковывать как неполный аккорд ii7 (без основного тона) ".^[3] Задержка принятия IV – I в финальных каденциях эстетически объясняется отсутствием замкнутости, вызванным его положением в круге квинт. Более раннее использование IV – V – I объясняется предложением связи между IV и ii, позволяя IV заменять или служить в качестве ii. Однако Наттис называет этот последний аргумент «узким бегством: только теория аккорда ii без корень позволяет Goldman утверждать, что круг пятых полностью действителен с Бах к Вагнер ", или весь период общей практики.^[5]

Замыкание круга в неравных системах настройки

Когда инструмент настроен с помощью равный темперамент система, ширина пятых такова, что круг «замыкается». Это означает, что, поднявшись на двенадцать пятых от любой высоты звука, человек возвращается к тону точно того же класса высоты звука, что и исходный тон, и ровно семь октавы над ним. Чтобы получить такое идеальное замыкание круга, пятая часть слегка приплюснута относительно ее просто интонация (3:2 соотношение интервалов ).

Таким образом, восхождение с помощью правильно настроенных квинт не может замкнуть круг с превышением примерно на 23,46. центы, примерно четверть полутон, интервал, известный как Пифагорейская запятая. В настройке Пифагора эта проблема решается за счет значительного сокращения ширина одной из двенадцати пятых, что серьезно диссонирующий. Эта аномальная пятая часть называется волк пятый как юмористическая метафора неприятного звука ноты (как волк, пытающийся выть нестандартной нотой). В четверть запятой означает один Система настройки использует одиннадцать пятых немного уже, чем такая же темперированная квинта, и требует гораздо более широкую и даже более диссонирующую волчью пятую часть, чтобы замкнуть круг. Более сложные системы настройки на основе просто интонация, Такие как 5-предельная настройка используйте не более восьми правильно настроенных квинт и по крайней мере три не только квинтэ (некоторые немного уже, а некоторые немного шире, чем только квинта), чтобы замкнуть круг. Другие системы настройки используют до 53 тона (исходные 12 тонов и еще 42 между ними), чтобы замкнуть круг квинт.

Говоря простым языком

Играя круг пятых
1 октава, четверти, по убыванию 1 октава, квинта, по возрастанию 2 октавы, квинта, по возрастанию 2 октавы, четверти, по убыванию 2 октавы, четверти, по возрастанию 2 октавы, квинта, по убыванию мультиоктава, квинта, по возрастанию мультиоктавная, четвертая, по убыванию мультиоктавный, четвертый, восходящий

Простой способ увидеть музыкальный интервал известный как пятый глядя на фортепианная клавиатура, и, начиная с любой клавиши, считая семь клавиш вправо (как черные, так и белые, не считая первой), чтобы перейти к следующей заметке в кружке, показанном выше. Семь полшага, расстояние от 1-й до 8-й тональности на фортепиано - это «идеальная квинта», называемая «идеальной», потому что она не является ни мажорной, ни минорной, но применяется как к мажорной, так и к минорной гамме и аккордам, и к «квинте», потому что хотя на клавиатуре это расстояние в семь полутонов, оно охватывает пять смежных нот в мажорной или минорной гамме.

Самый простой способ услышать взаимосвязь между этими нотами - сыграть их на клавиатуре фортепиано. При перемещении по кругу квинт назад ноты будут ощущаться так, как будто они падают друг в друга.^{[требуется разъяснение ]}. Эти слуховые отношения и описываются математикой.^{[нужна цитата ]}

Идеальные квинты могут быть справедливо настроенный или же закаленный. Две ноты, частоты которых различаются в соотношении 3: 2, делают интервал известным как точно настроенная идеальная квинта. Каскадирование двенадцати таких пятых не возвращает к исходному состоянию. класс поля после обхода круга, поэтому соотношение 3: 2 может быть слегка расстроено или смягчено. Темперамент позволяет циклически повторять идеальные квинты и транспонированный, или играл в любом ключ на пианино или другом инструменте с фиксированной высотой звука, не нарушая их гармонии. Основная система настройки, используемая для вестерн (особенно клавиатура и раздраженный ) инструменты сегодня, двенадцать тонов равный темперамент, использует иррациональный множитель, 2^1/12, чтобы вычислить разность частот полутона. Квинта с равномерным темпом при соотношении частот 2^7/12: 1 (или примерно 1,498307077: 1) примерно на два цента уже, чем правильно настроенная квинта при соотношении 3: 2.

История

Heinichen музыкальный кружок (немецкий: Musicalischer Circul)(1711)

Есть источники, которые предполагают, что Пифагор, древнегреческий философ шестого века до нашей эры. изобрели круг пятых, но они не предоставляют доказательств этого утверждения.^[6][7][8] Пифагор в первую очередь занимался теоретической наукой о гармониках, и считается, что он разработал систему настройки, основанную на интервале в одну квинту, но не настроил более восьми нот и не оставил никаких письменных записей о своей работе.^[9]

В конце 1670-х гг. научный труд называется Грамматика был написан украинским композитором и теоретиком Николай Дилецкий. Дилецкого Грамматика - трактат о композиции, «первый в своем роде, направленный на обучение русской аудитории тому, как писать полифонические композиции в западном стиле». Он научил писать Концерты, полифонический а капелла работает нормально на основе литургический тексты и созданы путем объединения музыкальных разделов, которые имеют контрастирующие ритм, метры, мелодичный материал и вокал группировки. Дилецкий задумал свой трактат как руководство по композиции, но относящийся к правилам теория музыки.

В трактате «Грамматика» появился первый круг квинты, который использовался студентами как инструмент композитора.^[10]

Использовать

В музыкальных произведениях из Барочная музыка эпоха и Классическая эпоха музыки и в западных популярная музыка, традиционная музыка и Народная музыка, когда пьесы или песни модулируются в новой тональности, эти модуляции часто ассоциируются с кругом квинт.

На практике в композициях редко используется весь пятый круг. Чаще композиторы используют «композиционную идею« цикла »5-х, когда музыка последовательно проходит через меньший или больший сегмент тональных структурных ресурсов, которые абстрактно представляет круг».^[11] Обычная практика состоит в том, чтобы получить круг прогрессии квинт из семи тонов диатонической гаммы, а не из всего диапазона двенадцати тонов, присутствующих в хроматической гамме. В этой диатонической версии круга одна квинта не является истинной пятой: это тритон (или уменьшенная квинта), например между F и B в «естественной» диатонической гамме (то есть без диез или бемоль). Вот как возникает круг пятых через перестановка из диатонической мажорной гаммы:

Диатоническая гамма и производный от нее круг квинт - мажор

Диатоническая гамма и производный от нее круг квинт - мажор

И из (натуральной) минорной гаммы:

Диатоническая гамма и производный от нее круг квинт - минор

Диатоническая гамма и производный от нее круг квинт - минор

Ниже приводится базовая последовательность аккордов, которую можно построить поверх основной басовой линии:

Аккордовая прогрессия по кругу квинт - мажор

Аккордовая прогрессия по кругу квинт - мажор

И над второстепенным:

Аккордовая прогрессия по кругу квинт - минор

Аккордовая прогрессия по кругу квинт - минор

Добавление септаккорд к аккордам создает большее ощущение движения вперед к гармонии:

Аккордовая прогрессия по кругу квинт - минор с добавлением септатов

Аккордовая прогрессия по кругу квинт - минор с добавлением септатов

Эпоха барокко

В соответствии с Ричард Тарускин, Арканджело Корелли был самым влиятельным композитором, установившим паттерн как стандартную гармонику. "троп": «Именно во времена Корелли, в конце семнадцатого века, круг квинт« теоретизировался »как главный двигатель гармонического движения, и именно Корелли больше, чем любой другой композитор, воплотил эту новую идею в практику изложения. "^[12]

Цикл прогрессии квинт часто встречается в музыке И. С. Бах. Далее из Jauchzet Gott in Allen Landen, BWV 51, даже когда сольная басовая линия подразумевает, а не указывает задействованные аккорды:

Бах из басовой партии кантаты 51

Бах из Кантаты 51

Гендель использует круг пятой прогрессии как основу для Пассакалия часть из его сюиты № 6 для клавесина соль минор.

Гендель Пассакайль из Сюиты соль минор такты 1–4

Гендель Пассакайль из Сюиты соль минор такты 1–4

Барокко композиторы научились увеличивать «движущую силу» гармонии, порожденной кругом квинт, «добавляя септакты к большинству составляющих аккордов». «Эти седьмые, будучи диссонансами, создают потребность в разрешении, таким образом превращая каждое движение круга в одновременное облегчение и повторный стимулятор гармонического напряжения ... Следовательно, они используются для выразительных целей».^[13] Яркие отрывки, иллюстрирующие использование седьмых, встречаются в арии «Pena tiranna» в Гендель Опера 1715 года Амадиги ди Гаула  :

Гендель, ария "Pena tiranna" из оперы "Амадиги". Оркестровое вступление.

Гендель, ария "Pena tiranna" из оперы "Амадиги". Оркестровое вступление

- и у Баха расположение клавиатуры из Алессандро Марчелло с Концерт для гобоя и струнных.

Бах адажио BWV 974 (по Марчелло)

Бах адажио BWV 974 (по Марчелло)

Девятнадцатый век

В течение девятнадцатого века композиторы использовали круг квинты, чтобы усилить выразительный характер своей музыки. Франц Шуберт Пронзительный экспромт ми-бемоль мажор, D899, содержит такой отрывок:

Экспромт Шуберта в М-квартире

Экспромт Шуберта в М-квартире

- как и Интермеццо движение от Мендельсон с Струнный квартет No2:

Струнный квартет Мендельсона 2, часть 3 (Интермеццо)

Струнный квартет Мендельсона 2, часть 3 (Интермеццо)

Запоминающийся «Ребенок, засыпающий» Роберта Шумана Kinderszenen преподносит сюрприз в конце прогрессии: пьеса заканчивается на аккорде ля минор вместо ожидаемого тоник Ми минор.

Шуман, Kind im Einschlummern (Ребенок, засыпающий)

Шуман, Kind im Einschlummern

В Вагнер опера, Götterdämmerung, в музыке происходит цикл квинт-прогрессии, который переходит от конца пролога к первой сцене первого акта, действие которой происходит во внушительном зале богатых Gibichungs. «Статус и репутация написаны повсюду в мотивах, присвоенных Гюнтеру»,^[14] глава клана Гибичунг:

Вагнер, Gotterdamerung, переход между концом Пролога и сценой 1 Акта 1

Вагнер, Gotterdamerung, переход между концом Пролога и сценой 1 Акта 1

Равель с "Павана для мертвой инфанты", использует цикл квинт, чтобы вызвать гармонию барокко, чтобы передать сожаление и ностальгию по прошлой эпохе. Композитор охарактеризовал произведение как «воспоминание о паване что маленькая принцесса (инфанта ) мог бы в прежние времена танцевать при испанском дворе. ":^[15]

Ravel, Pavane pour une Infante Défunte

Ravel Pavane pour une Infante Défunte

Джаз и популярная музыка

Непреходящая популярность круга квинт как средства формирования формы и выразительного музыкального образа проявляется в числе "стандарт «популярные песни, сочиненные в двадцатом веке. Джазовые музыканты также предпочитают эту музыку как средство импровизации.

• Барт Ховард, "Лети меня на Луну "

Песня открывается набором нисходящих фраз - по сути, крючком песни - представленным с успокаивающей предсказуемостью, почти как если бы будущее направление мелодии было продиктовано начальными пятью нотами. В свою очередь, гармоническая прогрессия редко выходит за пределы круга квинт.^[16]

• Джером Керн, "Все, что вы есть "^[17]
• Рэй Ноубл, "Чероки. "Многим джазовым музыкантам это особенно сложно, поскольку средняя восьмерка прогрессирует так быстро по кругу ", создавая серию II – V – I прогрессии которые временно проходят через несколько тональности."^[18]
• Космо, Преверт и Мерсер "Осенние листья "^[19]
• Битлз, "Ты никогда не отдашь мне свои деньги "^[20]
• Майк Олдфилд, "Заклинания "^{[нужна цитата ]}
• Карлос Сантана, "Европа (Крик Земли, Улыбка Небес) "^{[нужна цитата ]}
• Глория Гейнор, "Я выживу "^[21]
• Зоомагазин мальчики, "Это грех "^[22]
• Донна Саммер, "Люблю любить тебя, детка "^[23]

Связанные понятия

Диатонический круг пятых

Основная статья: Прогресс по кругу

Диатонический круг квинт - это круг квинт, охватывающий только члены диатонической шкалы. Таким образом, он содержит уменьшенную пятую часть до мажор между B и F. См. структура предполагает множественность. круговая прогрессия обычно представляет собой круг квинт через диатонические аккорды, включая один уменьшенный аккорд. По кругу до мажор с аккордами I – IV – vii^о–Iii – vi – ii – V – I показано ниже.

Хроматический круг

Основная статья: Хроматический круг

Круг пятых тесно связан с хроматический круг, в котором также расположены двенадцать классов равномерного тембра в круговом порядке. Ключевое различие между двумя кругами заключается в том, что хроматический круг можно понимать как непрерывное пространство, где каждая точка на окружности соответствует мыслимому класс поля, и каждый мыслимый класс высоты тона соответствует точке на окружности. Напротив, круг пятых по сути своей дискретный структуры, и нет очевидного способа присвоить классы высоты тона каждой из ее точек. В этом смысле два круга математически совершенно разные.

Однако двенадцать равномерных классы поля может быть представлен циклическая группа порядка двенадцати, или, что эквивалентно, классы остатков по модулю двенадцать, ${\displaystyle \mathbb {Z} /12\mathbb {Z} }$. Группа ${\displaystyle \mathbb {Z} _{12}}$ имеет четыре генератора, которые можно отождествить с восходящими и нисходящими полутонами, а также с восходящими и нисходящими идеальными квинтами. Полутональный генератор дает хроматический круг в то время как идеальная квинта порождает круг квинтов.

Связь с хроматической шкалой

Основная статья: Хроматическая шкала

Круг квинт, нарисованный внутри хроматического круга как звезда додекаграмма.^[24]

Круг пятых или четвертых может быть нанесен на карту от хроматическая шкала к умножение, наоборот. Чтобы отобразить между пятым кругом и хроматической шкалой (в целочисленная запись ) умножить на 7 (M7 ), а для круга четвертей умножьте на 5 (P5).

Вот демонстрация этой процедуры. Начните с упорядоченный Кортеж из 12 (ряд тонов ) целых чисел

(0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11)

представляющие ноты хроматической гаммы: 0 = C, 2 = D, 4 = E, 5 = F, 7 = G, 9 = A, 11 = B, 1 = C♯, 3 = D♯, 6 = F♯, 8 = G♯, 10 = А♯. Теперь умножьте все 12 кортежей на 7:

(0, 7, 14, 21, 28, 35, 42, 49, 56, 63, 70, 77)

а затем применить по модулю Уменьшение на 12 до каждого числа (вычтите 12 из каждого числа столько раз, сколько необходимо, пока число не станет меньше 12):

(0, 7, 2, 9, 4, 11, 6, 1, 8, 3, 10, 5)

что эквивалентно

(C, G, D, A, E, B, F♯, С♯, ГРАММ♯, D♯, А♯, F)

который является пятым кругом. Обратите внимание, что это энгармонично эквивалент:

(C, G, D, A, E, B, G♭, D♭, А♭, E♭, B♭, F).

Энгармонические эквиваленты и теоретические ключи

Основная статья: Теоретический ключ

Ключевые подписи в нижней части круга пятой диаграммы, такие как D♭ major, часто пишутся в квартирах одним способом, а острым - другим. Эти ключи легко меняются местами с использованием энгармонических эквивалентов. Энгармонический означает, что ноты звучат одинаково, но пишутся по-разному. Например, подпись ключа D♭ мажор, с пятью квартирами, содержит те же энгармонические ноты, что и C♯ мажор (семь диезов).

После C♯ приходит ключ G♯ (по образцу того, что он на пятую часть выше и, по совпадению, энгармонически эквивалентен тональности A♭). «Восьмой диез» ставится на F♯, чтобы сделать F. Ключ D♯, с девятью диезом, на C♯, что делает его C. То же самое и с ключевыми подписями с квартирами; Тональность E (четыре диеза) эквивалентна тональности F♭ (снова на одну пятую ниже тональности C♭, по образцу плоских ключевых подписей). Последняя квартира находится на B♭, что делает его B. Такие ключи с двойной случайностью в подписях ключей называются теоретические ключи: их ключевые подписи появляются крайне редко, но иногда они тонизируются в процессе работы (особенно, если домашний ключ уже был сильно заострен или сплющен).

Не существует стандарта, как записывать теоретические ключевые подписи:

• Поведение по умолчанию Лилипруд (на фото выше) записывает все диезы (бемоль) в круге пятых, прежде чем перейти к двойным диерам. Это формат, используемый в Джон Фулдс ' Мировой реквием, Соч. 60, который заканчивается ключевой подписью G♯ основной (точно так, как показано выше, стр. 153ff. ) Дулы в ключевой сигнатуре G♯ майор здесь продолжить C♯, ГРАММ♯, D♯, А♯, E♯, B♯, F.
• Одиночные острые предметы или плоские метки в начале иногда повторяются в знак любезности, например Макс Регер с Дополнение к теории модуляции., который содержит D♭ второстепенные ключевые подписи на стр. 42–45. У них есть B♭ в начале, а также B в конце (с двойным плоским символом) идет B♭, E♭, А♭, D♭, ГРАММ♭, С♭, F♭, B. Соглашение LilyPond и Foulds подавило бы начальную букву B♭.
• Иногда в начале ключевой подписи пишутся двойные знаки, за которыми следуют одиночные знаки. Например, F♭ подпись ключа обозначается буквой B, E♭, А♭, D♭, ГРАММ♭, С♭, F♭. Это соглашение использует Виктор Эвальд в программе Finale (программное обеспечение),^[25] и некоторыми теоретическими работами.

Смотрите также

• Подходящий аккорд
• Форма сонаты
• Хороший темперамент
• Текстовая таблица круг пятых
• Созвездие питча
• Мультипликативная группа целых чисел по модулю n

Примечания

1. Майкл Пилхофер и Холли Дэй (23 февраля 2009 г.). "Пятый круг: краткая история", www.dummies.com.
2. Наттис 1990, п. 225.
3. Гольдман 1965, п. 68.
4. Гольдман 1965, Глава 3.
5. Наттис 1990, п. 226.
6. Анон. "Пятый круг: краткая история". Dummies.com.^{[неудачная проверка ]}
7. https://www.classicfm.com/discover-music/music-theory/what-is-the-circle-of-fifths/. Отсутствует или пусто | название = (помощь)^{[неудачная проверка ]}
8. Анон. (2016). «Пятый круг».^{[неудачная проверка ]}
9. Фрейзер, Питер А. (2001). «Развитие музыкальных систем настройки» (PDF): 9, 13. Получено 24 мая 2020. (архив от 1 июля 2013 г.).
10. Дженсен 1992 С. 306–307.
11. Whittall, A. (2002, стр. 259) "Circle of Fifths", статья в Latham, E. (ed.) Oxford Companion to Music. Издательство Оксфордского университета.
12. Тарускин Р. (2010, с. 184) Оксфордская история западной музыки: музыка семнадцатого и восемнадцатого веков. Издательство Оксфордского университета.
13. Тарускин Р. (2010, с. 188) Оксфордская история западной музыки: музыка семнадцатого и восемнадцатого веков. Издательство Оксфордского университета.
14. Скратон, Р. (2016, стр. 121) Кольцо истины: Мудрость Вагнеровского кольца нибелунга. Лондон, Аллен Лейн.
15. Андрес, Роберт, "Введение в сольную фортепианную музыку Дебюсси и Равеля", BBC Radio 3, доступ 17 ноября 2011 г.
16. Джоа, Т. (2012, стр.115) Джазовые стандарты; Путеводитель по репертуару. Издательство Оксфордского университета.
17. Джоа, Т. (2012, стр. 16) Джазовые стандарты; Путеводитель по репертуару. Издательство Оксфордского университета.
18. Скотт, Ричард Дж. (2003, стр. 123) Аккорды для авторов песен. Блумингтон, Индиана, Пресса Клуба писателей.
19. Костка, Стефан; Пейн, Дороти; Альмен, Байрон (2013). Тональная гармония с введением в музыку ХХ века (7-е изд.). Нью-Йорк: Макгроу-Хилл. С. 46, 238. ISBN  978-0-07-131828-0.
20. «Ты никогда не отдашь мне свои деньги» (1989, стр. 1099-1100, такты 1-16) Полные партитуры The Beatles. Хэл Леонард.
21. Фекарис Д. и Перрен Ф.Дж. (1978) Я выживу. Polygram International Publishing.
22. Теннант Н. и Лоу К. (1987, такты 1–8) «Это грех». Sony / ATV Music Publishing (UK) Ltd.
23. Мородер, Г., Беллот, П. и Саммер, Д. (1975, такты 11–14) "Love to Love you, Baby", авторское право 1976, Bulle Music Inc.
24. Маккартин 1998, п. 364.
25. https://www.hickeys.com/music/brass/brass_ensembles/brass_quintets/products/sku035994-ewald-victor-quintet-no-4-in-ab-op-8.php

Рекомендации

• Гольдман, Ричард Франко (1965). Гармония в западной музыке. Нью-Йорк: У. В. Нортон.
• Дженсен, Клаудия Р. (1992). «Теоретическое произведение конца XVII века в Московии:« Грамматика »Николая Дилецкого и древнейший круг пятых». Журнал Американского музыковедческого общества. 45 (2 (Лето)): 305–331. JSTOR  831450.
• Маккартин, Брайан Дж. (1998). «Прелюдия к музыкальной геометрии». Математический журнал колледжа. 29 (5 (ноябрь)): 354–370. JSTOR  2687250. Архивировано из оригинал на 2008-05-17. Получено 2008-07-29.
• Наттиз, Жан-Жак (1990). Музыка и дискурс: к семиологии музыки, переведенный Кэролайн Аббат. Принстон, Нью-Джерси: Издательство Принстонского университета. ISBN  0-691-02714-5. (Первоначально опубликовано на французском языке, как Musicologie générale et sémiologie. Париж: К. Бургуа, 1987. ISBN  2-267-00500-Х).

дальнейшее чтение

• Д'Инди, Винсент (1903). Cours de Composition Musicale. Париж: A. Durand et fils.
• Лестер, Джоэл. Между модами и ключами: немецкая теория, 1592–1802 гг.. 1990.
• Миллер, Майкл. Полное руководство идиота по теории музыки, 2-е изд.. [Индианаполис, Индиана]: Альфа, 2005. ISBN  1-59257-437-8.
• Пурвинс, Хендрик (2005) ".Профили классов высоты звука: круговорот относительной высоты звука и тональности - эксперименты, модели, компьютерный анализ музыки и перспективы ". Докторская диссертация. Берлин: Technische Universität Berlin.
• Пурвинс, Хендрик, Бенджамин Бланкерц и Клаус Обермайер (2007). "Тороидальные модели в тональной теории и анализе питч-класса ". в: Вычислительная техника в музыковедении 15 («Тональная теория для цифровой эпохи»): 73–98.

внешняя ссылка

• Расшифровка круга Vths
• Интерактивный круг пятых с гитарным грифом
• Интерактивный кружок квинт с открытым исходным кодом для гитаристов
• Четвертый круг: оркестровая увертюра с использованием круга в качестве аккорда и мелодического элемента