Услышав форму барабана - Hearing the shape of a drum

Математически идеальные барабаны с мембранами этих двух разных форм (но в остальном идентичны) будут звучать одинаково, потому что собственные частоты все равны, поэтому тембровые спектры будет содержать те же обертоны. Этот пример был построен Гордоном, Уэббом и Вольпертом. Обратите внимание, что оба полигона имеют одинаковую площадь и периметр.

К услышать форму барабана заключается в том, чтобы вывести информацию о форме барабан от звука, который он издает, т. е. из списка обертоны, с использованием математический теория.

"Можно ли услышать форму барабана?" это название статьи 1966 года автора Марк Кац в Американский математический ежемесячный журнал что сделало вопрос известным, хотя эта конкретная формулировка происходит от Липман Берс. Подобные вопросы можно проследить вплоть до Герман Вейль. За свою статью Кацу дали Премия Лестера Р. Форда в 1967 г. и Приз Шовене в 1968 г.^[1]

Частоты, на которых может колебаться пластина барабана, зависят от ее формы. В Уравнение Гельмгольца вычисляет частоты, если форма известна. Эти частоты являются собственные значения из Лапласиан в пространстве. Центральный вопрос заключается в том, можно ли предсказать форму, если известны частоты; например, можно ли таким образом распознать кругообразный треугольник.^[2] Кац признал, что не знает, возможно ли, чтобы две разные формы давали одинаковый набор частот. На вопрос, определяют ли частоты форму, окончательно ответили отрицательно в начале 1990-х Гордон, Уэбб и Вольперт.

Официальное заявление

Более формально барабан задуман как эластичная мембрана, граница которой зажата. Он представлен как домен D в самолет. Обозначим через λ_п то Собственные значения Дирихле за D: это собственные значения из Задача Дирихле для Лапласиан:

{ displaystyle { begin {cases} Delta u + lambda u = 0 u | _ { partial D} = 0 end {cases}}}

Говорят, что два домена изоспектральный (или омофонические), если они имеют одинаковые собственные значения. Термин «омофонический» оправдан, потому что собственные значения Дирихле - это как раз основные тоны, которые способен воспроизводить барабан: они естественным образом выглядят как Коэффициенты Фурье в растворе волновое уравнение с зажатой границей.

Поэтому вопрос можно переформулировать так: что можно сделать вывод о D если известны только значения λ_п? Или, более конкретно: существуют ли два различных домена, которые являются изоспектральными?

Связанные с этим задачи могут быть сформулированы для задачи Дирихле для лапласиана на областях более высоких размерностей или на Римановы многообразия, а также для других эллиптические дифференциальные операторы такой как Оператор Коши – Римана или же Оператор Дирака. Другие граничные условия, помимо условия Дирихле, такие как Граничное условие Неймана, могут быть наложены. Видеть спектральная геометрия и изоспектральный как статьи по теме.

Ответ

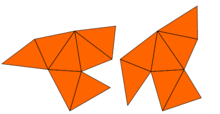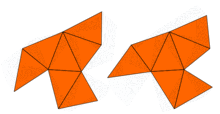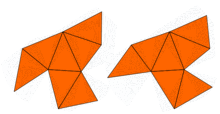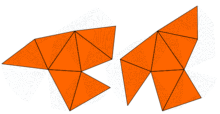
Однопараметрическое семейство изоспектральных барабанов

Почти сразу же, Джон Милнор заметил, что теорема из Эрнст Витт подразумевает существование пары 16-мерных торов, имеющих одинаковые собственные значения, но разную форму. Однако проблема в двух измерениях оставалась открытой до 1992 г., когда Кэролайн Гордон, Дэвид Уэбб, а Скотт Вольперт построил на основе Метод Сунада, пара областей на плоскости, имеющих разные формы, но одинаковые собственные значения. Регионы вогнутые многоугольники. Доказательство того, что обе области имеют одинаковые собственные значения, использует симметрии лапласиана. Эта идея была обобщена Бузером и др., Построившими множество подобных примеров. Итак, ответ на вопрос Каца: для многих форм нельзя услышать форму барабана. полностью. Однако некоторую информацию можно вывести.

С другой стороны, Стив Зельдич доказал, что ответ на вопрос Каца положительный, если наложить ограничения на некоторые выпуклый плоские области с аналитический граница. Неизвестно, могут ли две невыпуклые аналитические области иметь одинаковые собственные значения. Известно, что множество областей, изоспектральных данной, компактно в C^∞ топология. Более того, сфера (например) спектрально жесткая, по Теорема сравнения собственных значений Ченга. Из результатов Осгуда, Филлипса и Сарнака также известно, что пространство модулей римановых поверхностей данного рода не допускает непрерывного изоспектрального потока через любую точку и компактно в топологии Фреше – Шварца.

Формула Вейля

Формула Вейля утверждает, что можно вывести площадь А барабана, подсчитав, насколько быстро λ_п расти. Мы определяем N(р) быть числом собственных значений меньше, чем р и мы получаем

{ displaystyle A = omega _ {d} ^ {- 1} (2 pi) ^ {d} lim _ {R to infty} { frac {N (R)} {R ^ {d / 2}}} ,}

куда d это размер и ${ displaystyle omega _ {d}}$ объем d-мерный шар. Вейль также предположил, что следующий член в приближении ниже даст периметр D. Другими словами, если L обозначает длину периметра (или площадь поверхности в более высоком измерении), тогда нужно иметь

{ Displaystyle , N (R) = (2 pi) ^ {- d} omega _ {d} AR ^ {d / 2} + { frac {1} {4}} (2 pi) ^ {-d + 1} omega _ {d-1} LR ^ {(d-1) / 2} + o (R ^ {(d-1) / 2}). ,}

Для гладкой границы это доказано Виктор Иврий в 1980 году. Множеству также не разрешается иметь двухпараметрическое семейство периодических геодезических, таких как сфера.

Гипотеза Вейля – Берри

Для негладких границ Майкл Берри предположил в 1979 году, что исправление должно быть порядка

{ Displaystyle R ^ {D / 2} ,}

куда D это Хаусдорфово измерение границы. Это было опровергнуто Дж. Броссардом и Р. А. Кармона, которые затем предложили заменить хаусдорфово измерение на размерность размер верхней коробки. На плоскости это было доказано, если граница имеет размерность 1 (1993 г.), но в основном опровергнута для более высоких измерений (1996 г.); оба результата получены Lapidus и Померанс.

Смотрите также

Колебания круговой мембраны
Гассманн трехместный
Изоспектральный
Спектральная геометрия
расширение система повторяющихся функций фракталы^[3]

Примечания

^ "Можно ли услышать форму барабана? | Математическая ассоциация Америки".
^ Кац, Марк (Апрель 1966 г.). "Можно ли услышать форму барабана?" (PDF). Американский математический ежемесячный журнал. 73 (4, часть 2): 16.
^ Arrighetti, W .; Героса, Г. (2005). Вы слышите фрактальное измерение барабана?. Прикладная и промышленная математика в Италии. Серия достижений математики для прикладных наук. 69. World Scientific. С. 65–75. arXiv:math.SP / 0503748. Дои:10.1142/9789812701817_0007. ISBN 978-981-256-368-2.

внешняя ссылка

Изоспектральные барабаны Тоби Дрисколл из Университета Делавэра
Некоторые плоские изоспектральные области Питер Бузер, Джон Хортон Конвей, Питер Дойл и Клаус-Дитер Земмлер
Барабаны, которые звучат одинаково Иварс Петерсон с веб-сайта математической ассоциации Америки
Вайсштейн, Эрик В. «Изоспектральные многообразия». MathWorld.
Бенгурия, Рафаэль Д. (2001) [1994], «Собственное значение Дирихле», Энциклопедия математики, EMS Press

[1] "Можно ли услышать форму барабана? | Математическая ассоциация Америки".

[2] Кац, Марк (Апрель 1966 г.). "Можно ли услышать форму барабана?" (PDF). Американский математический ежемесячный журнал. 73 (4, часть 2): 16.

[3] Arrighetti, W .; Героса, Г. (2005). Вы слышите фрактальное измерение барабана?. Прикладная и промышленная математика в Италии. Серия достижений математики для прикладных наук. 69. World Scientific. С. 65–75. arXiv:math.SP / 0503748. Дои:10.1142/9789812701817_0007. ISBN 978-981-256-368-2.

[1]

[2]

[3]