Пять точек определяют конус - Five points determine a conic

В евклидовом и проективном геометрия, так же, как две (различные) точки определяют линия (плоская кривая степени 1), пять баллов определяют конический (плоская кривая степени 2). Для коник есть дополнительные тонкости, которых нет для прямых, и поэтому утверждение и его доказательство для коник более технические, чем для прямых.

Формально, учитывая любые пять точек на плоскости в общее линейное положение, то есть нет три коллинеарен, через них проходит единственная коника, которая будет невырожденной; это верно как для Евклидова плоскость и любой паппова проективная плоскость. Действительно, для любых пяти точек через них проходит коника, но если три точки лежат на одной прямой, то коника будет выродиться (сводится, потому что содержит строку) и не может быть уникальным; видеть дальнейшее обсуждение.

Доказательства

Этот результат можно доказать множеством разных способов; аргумент подсчета размерностей является наиболее прямым и обобщает до более высокой степени, в то время как другие доказательства являются специальными для коник.

Подсчет размеров

Интуитивно, прохождение пяти точек в общем линейном положении определяет пять независимых линейных ограничений на (проективное) линейное пространство коник и, следовательно, определяет уникальную конику, хотя это краткое утверждение игнорирует тонкости.

Точнее, это выглядит так:

коники соответствуют точкам в пятимерном проективном пространстве ${ Displaystyle mathbf {P} ^ {5};}$
требование прохождения коники через точку накладывает линейное условие на координаты: для фиксированного ${ Displaystyle (х, у),}$ уравнение ${ displaystyle Ax ^ {2} + Bxy + Cy ^ {2} + Dx + Ey + F = 0}$ это линейный уравнение в ${ displaystyle (A, B, C, D, E, F);}$
к подсчет размеров, пять ограничений (кривая проходит через пять точек) необходимы для задания конуса, поскольку каждое ограничение сокращает размерность возможностей на 1, а одно начинается с 5 измерений;
в 5 измерениях пересечение 5 (независимых) гиперплоскостей представляет собой единую точку (формально Теорема Безу );
общее линейное положение точек означает, что ограничения независимый, и таким образом укажите уникальную конику;
полученная коника невырожденная, потому что это кривая (поскольку она имеет более 1 точки) и не содержит линии (иначе она будет разделена на две линии, по крайней мере одна из которых должна содержать 3 из 5 точек, посредством принцип голубятни ), поэтому она неприводима.

Две тонкости в приведенном выше анализе заключаются в том, что результирующая точка представляет собой квадратное уравнение (а не линейное уравнение) и что ограничения независимы. Первый простой: если А, B, и C все обращаются в нуль, тогда уравнение ${ displaystyle Dx + Ey + F = 0}$ определяет линию, и любые 3 точки на ней (на самом деле любое количество точек) лежат на прямой - таким образом, общее линейное положение обеспечивает конику. Второе, что ограничения независимы, значительно тоньше: оно соответствует тому факту, что для пяти точек в общем линейном положении на плоскости их изображения в ${ displaystyle mathbf {P} ^ {5}}$ под Карта Веронезе находятся в общем линейном положении, что верно, потому что карта Веронезе двурегулярный: то есть, если изображение пяти точек удовлетворяет отношению, то отношение может быть восстановлено, и исходные точки также должны удовлетворять отношению. На карте Веронезе указаны координаты ${ displaystyle [x ^ {2}: xy: y ^ {2}: xz: yz: z ^ {2}],}$ и цель ${ displaystyle mathbf {P} ^ {5}}$ является двойной к ${ displaystyle [A: B: C: D: E: F]}$ ${ displaystyle mathbf {P} ^ {5}}$ коников. Карта Веронезе соответствует «вычислению коники в точке», а утверждение о независимости ограничений является в точности геометрическим утверждением об этой карте.

Синтетическое доказательство

То, что пять пунктов определяют конус, может быть доказано синтетическая геометрия - т.е. в терминах прямых и точек на плоскости - в дополнение к аналитическому (алгебраическому) доказательству, приведенному выше. Такое доказательство можно дать с помощью теоремы Якоб Штайнер,^[1] в котором говорится:

Учитывая проективное преобразование е, между пучком линий, проходящих через точку Икс и пучок прямых, проходящих через точку Y, набор C точек пересечения линии Икс и его образ

{ displaystyle f (x)}

образует конус.

Обратите внимание, что Икс и Y находятся на этой конусе, учитывая прообраз и образ линии XY (что, соответственно, является линией через Икс и линия через Y).

Это можно показать, взяв точки Икс и Y к стандартным точкам ${ displaystyle [1: 0: 0]}$ и ${ displaystyle [0: 1: 0]}$ проективным преобразованием, и в этом случае пучки прямых соответствуют горизонтальным и вертикальным линиям на плоскости, а пересечения соответствующих прямых - графику функции, которая (должна быть показана) является гиперболой, следовательно, коникой, следовательно, исходная кривая C коническая.

Теперь дано пять баллов X, Y, A, B, C, три линии ${ displaystyle XA, XB, XC}$ можно отнести к трем строкам ${ displaystyle YA, YB, YC}$ единственным проективным преобразованием, поскольку проективные преобразования просто 3-транзитивны по прямым (они просто 3-транзитивны по точкам, следовательно, по проективная двойственность они 3-транзитивны по линиям). Под этой картой Икс сопоставляется с Y, так как это единственные точки пересечения этих прямых и, таким образом, удовлетворяют условию теоремы Штейнера. Таким образом, получившаяся коника содержит все пять точек и является единственной такой коникой, как и требовалось.

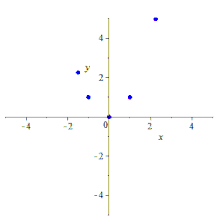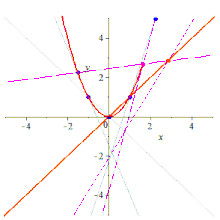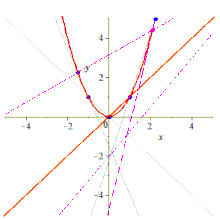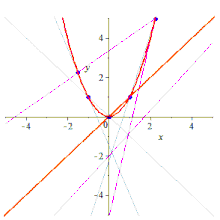
Построение параболы с учетом пяти баллов

Строительство

По пяти точкам можно по-разному построить конику, содержащую их.

Аналитически с учетом координат ${ displaystyle (x_ {i}, y_ {i}) _ {i = 1,2,3,4,5}}$ из пяти точек уравнение для коники можно найти следующим образом: линейная алгебра, записывая и решая пять уравнений в коэффициентах, заменяя переменные значениями координат: пять уравнений, шесть неизвестных, но однородные, поэтому масштабирование удаляет одно измерение; в частности, установка одного из коэффициентов на 1 позволяет добиться этого.

Это может быть достигнуто совершенно напрямую с помощью следующего детерминантного уравнения:

{ displaystyle det { begin {bmatrix} x ^ {2} & xy & y ^ {2} & x & y & 1 x_ {1} ^ {2} & x_ {1} y_ {1} & y_ {1} ^ {2} & x_ { 1} & y_ {1} & 1 x_ {2} ^ {2} & x_ {2} y_ {2} & y_ {2} ^ {2} & x_ {2} & y_ {2} & 1 x_ {3} ^ { 2} & x_ {3} y_ {3} & y_ {3} ^ {2} & x_ {3} & y_ {3} & 1 x_ {4} ^ {2} & x_ {4} y_ {4} & y_ {4} ^ {2} & x_ {4} & y_ {4} & 1 x_ {5} ^ {2} & x_ {5} y_ {5} & y_ {5} ^ {2} & x_ {5} & y_ {5} & 1 end { bmatrix}} = 0}

Эта матрица имеет переменные в своей первой строке и числа во всех остальных строках, поэтому определитель явно представляет собой линейную комбинацию шести одночленов степени не выше 2. Кроме того, результирующий многочлен явно обращается в нуль в пяти входных точках (когда ${ Displaystyle (х, у) = (х_ {я}, у_ {я})}$ ), так как тогда матрица имеет повторяющуюся строку.

Синтетически конику можно построить с помощью Конструкция Брейкенриджа – Маклорена,^[2]^[3]^[4]^[5] применяя Теорема Брейкенриджа – Маклорена, что является обратным Теорема Паскаля. Теорема Паскаля утверждает, что данный 6 точки на конике (шестиугольнике), прямые, определяемые противоположными сторонами, пересекаются в трех коллинеарных точках. Это можно изменить, чтобы построить возможные местоположения для 6-й точки, учитывая 5 существующих.

Обобщения

Естественное обобщение - спросить, какое значение k конфигурация k баллов (в общем положении) в п-пространство определяет множество степеней d и размер м, что является фундаментальным вопросом в перечислительная геометрия.

Простой случай - для гиперповерхность (а коразмерность 1 подмногообразие, нули одного многочлена, случай ${ Displaystyle м = п-1}$ ), примером которых являются плоские кривые.

В случае гиперповерхности ответ дается в терминах коэффициент мультимножества, более привычно биномиальный коэффициент, или более элегантно возрастающий факториал, в качестве:

{ displaystyle k = left (! ! {n + 1 select d} ! ! right) -1 = {n + d select d} -1 = { frac {1} {n! }} (d + 1) ^ {(n)} - 1.}

Это через аналогичный анализ Карта Веронезе: k баллы в общем положении накладывают k независимых линейных условий на многообразии (поскольку отображение Веронезе бирегулярно), а количество одночленов степени d в ${ displaystyle n + 1}$ переменные (п-мерное проективное пространство имеет ${ displaystyle n + 1}$ однородные координаты) ${ displaystyle textstyle { left (! ! {n + 1 выберите d} ! ! right)},}$ из которого вычитается 1 из-за проективизации: умножение многочлена на константу не меняет его нулей.

В приведенной выше формуле количество баллов k является многочленом от d степени п, с ведущим коэффициентом ${ Displaystyle 1 / п!}$

В случае плоских кривых, где ${ Displaystyle п = 2,}$ формула становится:

{ displaystyle textstyle { frac {1} {2}} (d + 1) (d + 2) -1 = textstyle { frac {1} {2}} (d ^ {2} + 3d)}

чьи значения для ${ displaystyle d = 0,1,2,3,4}$ находятся ${ displaystyle 0,2,5,9,14}$ - нет кривых степени 0 (одна точка является точкой и, таким образом, определяется точкой, которая имеет коразмерность 2), 2 точки определяют линию, 5 точек определяют конику, 9 точек определяют кубику, 14 точек определяют квартика и так далее.

Связанные результаты

Хотя пять точек определяют конику, наборы из шести или более точек на конике не находятся в общем положении, то есть они ограничены, как показано на Теорема Паскаля.

Точно так же, хотя девять точек определяют кубику, если девять точек лежат более чем на одной кубике, т.е. они являются пересечением двух кубиков, то они не находятся в общем положении и действительно удовлетворяют дополнительному ограничению, как указано в Теорема Кэли – Бахараха.

Четыре точки определяют не конус, а скорее карандаш, одномерная линейная система коник которые все проходят через четыре точки (формально имеют четыре точки как базовый локус ). Точно так же три точки определяют 2-мерную линейную систему (сеть), две точки определяют 3-мерную линейную систему (ткань), одна точка определяет 4-мерную линейную систему, а нулевые точки не накладывают ограничений на 5-мерную линейную систему. система всех коников.

В Аполлонические круги два однопараметрических семейства, определяемые двумя точками.

Как хорошо известно, три неколлинеарных точки определяют окружность в евклидовой геометрии, а две различные точки определяют круг. карандаш кругов такой как Аполлонические круги. Эти результаты, кажется, противоречат общему результату, поскольку окружности являются частным случаем коник. Однако в паппионе проективная плоскость коника - это круг, только если она проходит через две определенные точки на линия на бесконечности, поэтому окружность определяется пятью неколлинеарными точками, тремя на аффинной плоскости и этими двумя особыми точками. Подобные соображения объясняют меньшее, чем ожидалось, количество точек, необходимое для определения пучков окружностей.

Касательность

Вместо того, чтобы проходить через точки, другое условие на кривой касается касательной к данной линии. Касательная к пяти данным прямым также определяет конику посредством проективная двойственность, но с алгебраической точки зрения касание прямой - это квадратичный ограничение, поэтому наивный подсчет измерений дает 2⁵ = 32 коники, касательные к пяти заданным прямым, из которых 31 должна быть отнесена к вырожденным коникам, как описано в ложные факторы в перечислительной геометрии; Формализация этой интуиции требует значительного дальнейшего развития для обоснования.

Еще одна классическая проблема перечислительной геометрии, похожая на коническую, - это Проблема Аполлония: окружность, которая касается трех окружностей, в общем случае определяет восемь окружностей, поскольку каждая из них является квадратичным условием и 2³ = 8. Что касается реальной геометрии, полный анализ включает в себя множество частных случаев, и фактическое количество кругов может быть любым числом от 0 до 8, за исключением 7.

Смотрите также

Теорема Крамера (алгебраические кривые), для обобщения на пплоские кривые -й степени

внешняя ссылка

Пять точек определяют коническое сечение, Интерактивная демонстрация Wolfram

[1] Интерактивный курс по проективной геометрии, Глава пятая: Проективная геометрия коник: Раздел четвертый: Коники на реальной проективной плоскости, Х.С. Альварес Пайва; Доказательство следует из упражнения 4.6.

[2] (Коксетер 1961, стр. 252–254).

[3] Анимированный Паскаль, Сандра Лах Арлингхаус

[4] Вайсштейн, Эрик В. «Строительство Брейкенриджа-Маклорена». Материал из MathWorld - веб-ресурса Wolfram. http://mathworld.wolfram.com/Braikenridge-MaclaurinConstruction.html

[5] Страница конических разделов GNU 3DLDF: Теорема Паскаля и конструкция Брейкенриджа-Маклорена, Лоуренс Д. Финстон

[1]

[2]

[3]

[4]

[5]