Парадокс крамерса - Cramers paradox
В математика, Парадокс Крамера или Парадокс Крамера – Эйлера[1] - утверждение, что количество точек пересечения двух кривых высшего порядка в самолет может быть больше, чем количество произвольных точек, которые обычно требуются для определения одной такой кривой. Он назван в честь Женева математик Габриэль Крамер.
Этот парадокс является результатом наивного понимания или неправильного применения двух теорем:
- Теорема Безу (количество точек пересечения двух алгебраические кривые равна произведению их степеней при соблюдении определенных необходимых условий).
- Теорема Крамера (кривая степени п определяется п(п + 3) / 2 балла, опять же при выполнении определенных условий).
Обратите внимание на это для всех п ≥ 3, п2 ≥ п(п + 3) / 2, поэтому наивно могло бы показаться, что для степени три или выше может быть достаточно точек, общих для каждой из двух кривых, чтобы эти точки однозначно определяли любую из кривых.
Разрешение парадокса состоит в том, что в некоторых вырожденных случаях п(п + 3) / 2 балла недостаточно для однозначного определения кривой.
История
Парадокс был впервые опубликован Колин Маклорен.[2][3] Крамер и Леонард Эйлер писал о парадоксе в письмах 1744 и 1745 годов, и Эйлер объяснил проблему Крамеру.[4] Он стал известен как Парадокс Крамера после показа в его книге 1750 года Introduction à l'analyse des lignes courbes algébriques, хотя Крамер процитировал Маклорена как источник заявления.[5] Примерно в то же время Эйлер опубликовал примеры, показывающие кубическую кривую, которая не была однозначно определена 9 точками.[4][6] и обсуждал проблему в своей книге Введение в анализин бесконечный. Результат был опубликован Джеймс Стирлинг и объяснил Юлиус Плюкер.[1]
Никакого парадокса для прямых и невырожденных коник
Для кривых первого порядка (т.е. линии ) парадокса не возникает, потому что п = 1 поэтому п2 = 1 < п(п + 3) / 2 = 2. В общем, две различные линии L1 и L2 пересекаться в одной точке п кроме случаев, когда линии имеют одинаковый уклон (наклон), и в этом случае они вообще не пересекаются. Одной точки недостаточно для определения линии (нужны две); через точку п проходят не только две заданные строки, но и бесконечное количество других строк.
Аналогичным образом две невырожденные коники пересекаются не более чем в 4 конечных точках на вещественной плоскости, что меньше, чем 32 = 9, заданное как максимум по теореме Безу, и 5 точек необходимы для определения невырожденной коники.
Пример Крамера для кубических кривых
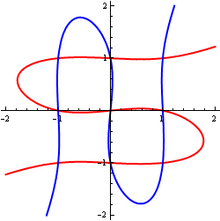
В письме Эйлеру Крамер указал, что кубические кривые Икс3 − Икс = 0 и у3 − у = 0 пересекаются ровно в 9 точках (каждое уравнение представляет собой набор из трех параллельных прямых Икс = −1, Икс = 0, Икс = +1; и у = −1, у = 0, у = +1 соответственно). Следовательно, 9 точек недостаточно для однозначного определения кубической кривой в таких вырожденных случаях, как этот.
Разрешение
Двумерное уравнение степени п имеет 1+ п(п + 3) / 2 коэффициентов, но набор точек, описываемых уравнением, сохраняется, если уравнение делится на один из коэффициентов, оставляя один коэффициент равным 1 и только п(п + 3) / 2 коэффициентов для характеристики кривой. Данный п(п + 3) / 2 балла (Икся, уя) каждая из этих точек может быть использована для создания отдельного уравнения, подставив его в общее полиномиальное уравнение степени п, давая п(п + 3) / 2 уравнения, линейных относительно п(п + 3) / 2 неизвестных коэффициента. Если эта система невырождена в смысле наличия ненулевого детерминант, неизвестные коэффициенты определяются однозначно и, следовательно, однозначно определяются полиномиальное уравнение и его кривая. Но если этот определитель равен нулю, система вырождена и точки могут находиться более чем на одной кривой степени п.
Рекомендации
- ^ а б Вайсштейн, Эрик В. «Парадокс Крамера-Эйлера». Материал из MathWorld - веб-ресурса Wolfram. http://mathworld.wolfram.com/Cramer-EulerParadox.html
- ^ Маклорен, Колин (1720). Геометрия Органика. Лондон.
- ^ Твиди, Чарльз (январь 1891 г.). "V. -" Geometria Organica "Колина Маклорена: исторический и критический обзор". Сделки Королевского общества Эдинбурга. 36 (1–2): 87–150. Получено 28 сентября 2012.
- ^ а б Струик, Д. Дж. (1969). Справочник по математике, 1200-1800 гг.. Издательство Гарвардского университета. п. 182. ISBN 0674823559.
- ^ Твиди, Чарльз (1915). "Исследование жизни и сочинений Колина Маклорена". Математический вестник. 8 (119): 133–151. JSTOR 3604693.
- ^ Эйлер, Л. "Sur une противоречивость apparente dans la doctrine des lignes courbes". Mémoires de l'Académie des Sciences de Berlin 4, 219-233, 1750
внешняя ссылка
- Эд Сэндифер "Парадокс Крамера"
- Парадокс Крамера на MathPages
