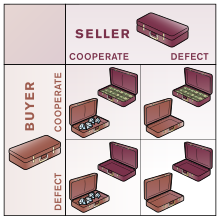
Дилемма заключенного - Prisoners dilemma

Для использования в других целях см. Дилемма заключенного (значения).

Не путать с Проблема трех узников.

Матрица выплат дилеммы заключенного

B А	B остается тихий	B предает
Остается тихий	-1 -1	0 -3
А предает	-3 0	-2 -2

В Дилемма заключенного стандартный пример игры, анализируемой в теория игры это показывает, почему два полностью рациональный отдельные лица могут не сотрудничать, даже если окажется, что это в их интересах. Первоначально он был оформлен Меррил Флуд и Мелвин Дрешер во время работы в RAND в 1950 г. Альберт В. Такер формализовала игру с наградами за тюремное заключение и назвала ее "дилеммой заключенного",^[1] представляя его следующим образом:

Два члена преступной группировки арестованы и заключены в тюрьму. Каждый заключенный находится в одиночном заключении, не имея возможности общаться друг с другом. У прокуратуры нет достаточных доказательств, чтобы осудить эту пару по основному обвинению, но у них есть достаточно, чтобы осудить обоих по менее серьезному обвинению. Одновременно прокуратура предлагает каждому заключенному выгодную сделку. Каждому заключенному предоставляется возможность либо предать другого, дав показания о том, что он совершил преступление, либо сотрудничать с другим, сохраняя молчание. Возможные результаты:

• Если A и B предают друг друга, каждый из них отбывает по два года тюрьмы.
• Если A предаст B, но B будет хранить молчание, A будет освобожден, а B отсидит три года в тюрьме.
• Если A будет хранить молчание, но B предаст A, A будет отсидеть три года в тюрьме, а B будет освобожден
• Если A и B оба будут молчать, они оба отсидят только один год тюрьмы (по меньшему обвинению).

Подразумевается, что у заключенных не будет возможности вознаградить или наказать своего партнера, кроме приговоров к тюремному заключению, которые они получили, и что их решение не повлияет на их репутацию в будущем. Поскольку предательство партнера предлагает большую награду, чем сотрудничество с ним, все чисто рациональные эгоистичные заключенные предадут друг друга, а это означает, что единственный возможный исход для двух чисто рациональных заключенных - это предать друг друга.^[2] В действительности люди демонстрируют системная предвзятость к кооперативному поведению в этой и подобных играх, несмотря на то, что предсказывают простые модели «рациональных» эгоистических действий.^[3][4][5][6] Этот уклон в сторону сотрудничества известен с тех пор, как испытание было впервые проведено в RAND; вовлеченные секретари доверяли друг другу и работали вместе для достижения наилучшего общего результата.^[7] Дилемма заключенного стала предметом обширных экспериментальных исследований.^[8][9]

Также существует расширенная «повторная» версия игры. В этой версии классическая игра многократно разыгрывается между одними и теми же заключенными, которые постоянно имеют возможность наказать другого за предыдущие решения. Если игрокам известно, сколько раз будет сыграна игра, то (по обратная индукция ) два классически рациональных игрока будут многократно предавать друг друга по тем же причинам, что и вариант с одиночным выстрелом. В игре с бесконечной или неизвестной продолжительностью не существует фиксированной оптимальной стратегии, и были проведены турниры по дилемме заключенного, чтобы соревноваться и проверять алгоритмы для таких случаев.^[10]

Игра «Дилемма заключенного» может служить моделью для многих. ситуации в реальном мире вовлечение кооперативного поведения. При случайном использовании ярлык «дилемма заключенного» может применяться к ситуациям, не строго соответствующим формальным критериям классических или итеративных игр: например, те, в которых два объекта могут получить важные выгоды от сотрудничества или пострадать от его отказа. , но им сложно или дорого - не обязательно невозможно - координировать свою деятельность.

Стратегия дилеммы заключенного

Два заключенных разделены по отдельным комнатам и не могут общаться друг с другом. Обычная игра показана ниже:

Заключенный B Заключенный А	Заключенный B молчит (сотрудничает)	Заключенный B предает (дефекты)
Заключенный молчит (сотрудничает)	Каждый обслуживает 1 год	Заключенный А: 3 года Заключенный B: выходит на свободу
Заключенный предает (дефекты)	Заключенный A: выходит на свободу Заключенный B: 3 года	Каждый служит 2 года

Предполагается, что оба заключенных понимают природу игры, не лояльны друг к другу и не будут иметь возможности для возмездия или вознаграждения вне игры. Независимо от того, что решит другой, каждый заключенный получает более высокую награду, предав другого («дезертирство»). Рассуждение включает аргумент дилемма: B будет либо сотрудничать, либо дезертировать. Если B будет сотрудничать, A должен уйти, потому что бесплатное обслуживание лучше, чем обслуживание в течение 1 года. Если дефект B, то A также должен дефект, потому что служить 2 года лучше, чем служить 3. Так что в любом случае A должен дефектить. Параллельное рассуждение покажет, что B должен уйти.

Поскольку отступничество всегда приносит больше выгоды, чем сотрудничество, независимо от выбора другого игрока, это доминирующая стратегия. Взаимное отступничество - единственное сильное равновесие по Нэшу в игре (т. е. единственный исход, из которого каждый игрок может сделать только хуже, если в одностороннем порядке изменит стратегию). Таким образом, дилемма состоит в том, что взаимное сотрудничество дает лучший результат, чем взаимное отступничество, но не является рациональным результатом, потому что выбор сотрудничества с эгоистической точки зрения иррационален.

Обобщенная форма

Структуру традиционной дилеммы заключенного можно обобщить, исходя из первоначальной обстановки заключенного. Предположим, что два игрока представлены красным и синим цветами, и что каждый игрок выбирает либо «сотрудничать» (молчать), либо «отступить» (предать).

Если оба игрока сотрудничают, они оба получают награду. р для сотрудничества. Если оба игрока отступают, они оба получают наказание. п. Если Синий не справляется, а Красный сотрудничает, то Синий получает искушение. Т, в то время как Красный получает "присоску", S. Точно так же, если Синий сотрудничает, а Красный - дефект, то Синий получает вознаграждение за присоски. S, а красный получает искушение Т.

Это можно выразить в нормальная форма:

Каноническая матрица выигрыша PD

красный Синий	Сотрудничать	Дефект
Сотрудничать	р р	Т S
Дефект	S Т	п п

и чтобы быть игрой дилеммы заключенного в строгом смысле этого слова, для выплат должно выполняться следующее условие:

${\displaystyle T>R>P>S}$

Отношения вознаграждения ${\displaystyle R>P}$ подразумевает, что взаимное сотрудничество превосходит взаимное отступничество, в то время как отношения компенсации ${\displaystyle T>R}$ и ${\displaystyle P>S}$ подразумевают, что дезертирство - это доминирующая стратегия для обоих агентов.

Особый случай: игра с пожертвованиями

«Игра в пожертвования»^[11] это форма дилеммы заключенного, в которой сотрудничество соответствует предложению другому игроку выгоды б за личную плату c с б > c. Отклонение означает ничего не предлагать. Таким образом, матрица выплат имеет вид

красный Синий	Сотрудничать	Дефект
Сотрудничать	б−c б−c	б −c
Дефект	−c б	0 0

Обратите внимание, что ${\displaystyle 2R>T+S}$ (т.е. ${\displaystyle 2(b-c)>b-c}$), что квалифицирует игру с пожертвованиями как повторную игру (см. следующий раздел).

Игра в пожертвования может применяться к рынкам. Предположим, X выращивает апельсины, Y выращивает яблоки. В предельная полезность яблока производителю апельсинов X составляет б, что выше предельной полезности (c) апельсина, так как у X избыток апельсинов и нет яблок. Аналогичным образом, для производителя яблок Y предельная полезность апельсина равна б в то время как предельная полезность яблока c. Если X и Y заключают договор об обмене яблоком и апельсином, и каждый выполняет свою часть сделки, то каждый получает выплату в размере б-c. Если один «дефект» и не доставит, как обещал, перебежчик получит выплату в размере б, а кооператор потеряет c. Если оба ошибаются, то ни один из них ничего не приобретает и не теряет.

Повторяющаяся дилемма заключенного

Если два игрока разыгрывают дилемму заключенного более одного раза подряд и помнят предыдущие действия своего оппонента и соответственно меняют свою стратегию, игра называется повторной дилеммой заключенного.

В дополнение к общей форме, приведенной выше, итеративная версия также требует, чтобы ${\displaystyle 2R>T+S}$, чтобы предотвратить чередование сотрудничества и отступничества, дающее большую награду, чем взаимное сотрудничество.

Повторяющаяся игра «дилемма заключенного» является фундаментальной для некоторых теорий человеческого сотрудничества и доверия. Исходя из предположения, что игра может моделировать транзакции между двумя людьми, требующими доверия, совместное поведение в популяциях может быть смоделировано многопользовательской повторяющейся версией игры. Следовательно, на протяжении многих лет он очаровывал многих ученых. В 1975 году Грофман и Пул подсчитали, что количество научных статей, посвященных этой теме, превысило 2000. Повторяющаяся дилемма заключенного также упоминается как "мирно-военная игра ".^[12]

Если игра ведется точно N раз, и оба игрока знают это, то оптимальным является дезертирство во всех раундах. Единственно возможный равновесие по Нэшу всегда отступать. Доказательство индуктивный: с таким же успехом можно дезертировать на последнем ходу, так как у оппонента не будет шанса нанести ответный удар. Следовательно, оба дезертируют в последний ход. Таким образом, игрок может также дезертировать на предпоследнем ходу, так как противник отступит на последнем, что бы ни было сделано, и так далее. То же самое применимо, если продолжительность игры неизвестна, но имеет известный верхний предел.

В отличие от стандартной дилеммы заключенного, в повторяющейся дилемме заключенного стратегия отступничества противоречит интуиции и плохо предсказывает поведение игроков-людей. Однако в рамках стандартной экономической теории это единственно правильный ответ. В сверхрациональный стратегия в повторяющейся дилемме заключенного с фиксированной N состоит в том, чтобы сотрудничать против сверхрационального противника, и в пределе больших N, экспериментальные результаты по стратегиям согласуются с суперрациональной версией, а не с теоретико-игровой рациональной.

За сотрудничество между теоретически рациональными игроками, общее количество раундов N должно быть неизвестно игрокам. В этом случае «всегда дефект» может больше не быть строго доминирующей стратегией, а только равновесием по Нэшу. Среди результатов, показанных Роберт Ауманн в статье 1959 года рациональные игроки, постоянно взаимодействующие в течение бесконечно длинных игр, могут поддерживать совместный исход.

Согласно экспериментальному исследованию 2019 г. Американский экономический обзор которые проверяли, какие стратегии использовали реальные субъекты в повторяющихся ситуациях дилеммы заключенных с идеальным мониторингом, большинство выбранных стратегий всегда были дефектными, око за око, и мрачный спусковой крючок. Выбор стратегии зависел от параметров игры.^[13]

Стратегия решения повторяющейся дилеммы заключенного

Интерес к повторной дилемме заключенного (IPD) был вызван Роберт Аксельрод в его книге Эволюция сотрудничества (1984). В нем он сообщает об организованном им турнире N дилемма заключенного (с N исправлено), в котором участники должны снова и снова выбирать свою общую стратегию и помнить о своих предыдущих встречах. Аксельрод пригласил академических коллег со всего мира разработать компьютерные стратегии для участия в турнирах IPD. Вводимые программы сильно различались по алгоритмической сложности, начальной враждебности, способности прощать и так далее.

Аксельрод обнаружил, что, когда эти встречи повторялись в течение длительного периода времени со многими игроками, каждый из которых имел разные стратегии, жадные стратегии, как правило, очень плохо работали в долгосрочной перспективе, в то время как больше альтруистический стратегии оказались лучше, если судить по чисто личным интересам. Он использовал это, чтобы показать возможный механизм эволюции альтруистического поведения из механизмов, которые изначально были чисто эгоистичными, посредством естественный отбор.

Победа детерминированный стратегия была око за око, что Анатолий Рапопорт разработан и вошел в турнир. Это была самая простая из введенных программ, содержащая всего четыре строки БАЗОВЫЙ, и выиграл конкурс. Стратегия состоит в том, чтобы просто сотрудничать на первой итерации игры; после этого игрок делает то же, что его противник делал на предыдущем ходу. В зависимости от ситуации немного лучшей стратегией может быть «око за око с прощением». Когда противник отступает, на следующем ходу игрок иногда все равно сотрудничает с небольшой вероятностью (около 1–5%). Это позволяет время от времени выздоравливать, чтобы не попасть в ловушку цикла отступничества. Точная вероятность зависит от состава противников.

Анализируя стратегии с наивысшими показателями, Аксельрод сформулировал несколько условий, необходимых для успеха стратегии.

Отлично

Самым важным условием является то, что стратегия должна быть «хорошей», то есть не допускать ошибок раньше, чем это сделает оппонент (это иногда называют «оптимистическим» алгоритмом). Почти все стратегии, набравшие наибольшее количество очков, были хороши; следовательно, чисто эгоистичная стратегия не будет «обманывать» своего оппонента, прежде всего из чисто корыстных соображений.

Мстительный

Однако, утверждал Аксельрод, успешная стратегия не должна быть слепым оптимистом. Иногда ему приходится принимать ответные меры. Пример стратегии невозмездия - «Всегда сотрудничать». Это очень плохой выбор, так как «противные» стратегии будут безжалостно эксплуатировать таких игроков.

Прощение

Успешные стратегии также должны прощать. Хотя игроки будут принимать ответные меры, они снова вернутся к сотрудничеству, если противник не будет продолжать отступать. Это останавливает длительные периоды мести и контр-мести, максимизируя очки.

Не завистливый

Последнее качество - отсутствие зависти, то есть не стремление набрать больше очков, чем соперник.

Оптимальная стратегия (максимизация очков) для одноразовой игры PD - это просто отступничество; Как объяснялось выше, это верно независимо от состава оппонентов. Однако в игре с итеративным PD оптимальная стратегия зависит от стратегий вероятных противников и того, как они будут реагировать на отступничество и сотрудничество. Например, представьте себе популяцию, в которой все каждый раз сбегают, за исключением одного человека, который следует стратегии «око за око». Этот человек находится в небольшом невыгодном положении из-за проигрыша в первый ход. В такой популяции оптимальная стратегия для этого человека - каждый раз дезертировать. В популяции с определенным процентом постоянных перебежчиков и остальными игроками за око оптимальная стратегия для отдельного человека зависит от процента и от продолжительности игры.

В стратегии Павлова беспроигрышный, проигрышный столкнувшись с отказом от сотрудничества, игрок меняет стратегию на следующем ходу.^[14] При определенных обстоятельствах^{[уточнить ]} Павлов превосходит все другие стратегии, отдавая предпочтение товарищам по игре, используя аналогичную стратегию.

Получение оптимальной стратегии обычно осуществляется двумя способами:

• Байесовское равновесие по Нэшу: Если можно определить статистическое распределение противоположных стратегий (например, 50% оскорблений за око, 50% всегда сотрудничают), оптимальная контрстратегия может быть получена аналитически.^[а]
• Монте-Карло было выполнено моделирование популяций, где особи с низкими показателями умирают, а особи с высокими показателями воспроизводятся ( генетический алгоритм для поиска оптимальной стратегии). Сочетание алгоритмов в конечной популяции обычно зависит от состава исходной популяции. Введение мутации (случайное изменение во время размножения) снижает зависимость от исходной популяции; эмпирические эксперименты с такими системами, как правило, приводят к получению «око за око» (см., например, Chess 1988),^{[требуется разъяснение ]} но не существует аналитических доказательств того, что это всегда будет происходить.^[16]

Хотя око за око считается самым крепкий базовая стратегия, команда из Саутгемптонский университет в Англии представили новую стратегию на соревновании по повторной дилемме заключенного, посвященном 20-летию, которое оказалось более успешным, чем око за око. Эта стратегия основывалась на сговоре между программами для достижения наибольшего количества баллов за одну программу. Университет представил на конкурс 60 программ, которые были разработаны так, чтобы узнавать друг друга через серию из пяти-десяти ходов на старте.^[17] Как только это признание будет сделано, одна программа всегда будет сотрудничать, а другая всегда будет давать сбой, обеспечивая максимальное количество баллов для перебежчика. Если бы программа понимала, что играет игрок, не являющийся игроком «Саутгемптона», она будет постоянно отказываться от попыток минимизировать счет конкурирующей программы. В результате, результаты турнира 2004 года "Дилемма заключенных" показывают Саутгемптонский университет стратегии на первых трех местах, несмотря на меньшее количество побед и намного больше проигрышей, чем стратегия GRIM. (В турнире PD цель игры не в том, чтобы «выиграть» матчи - этого легко добиться частым дезертирством). Кроме того, даже без неявного сговора между программные стратегии (используется командой Саутгемптона) «око за око» не всегда является абсолютным победителем любого данного турнира; точнее было бы сказать, что его долгосрочные результаты по серии турниров превосходят его соперников. (В любом случае данная стратегия может быть немного лучше приспособлена к соревнованиям, чем «око за око», но «око за око» более надежна). То же самое относится к варианту «око за око» с вариантом прощения и другим оптимальным стратегиям: в любой конкретный день они могут не «выиграть» против определенного набора контр-стратегий. Альтернативный способ выражения - использование дарвиновского ESS моделирование. В такой симуляции «око за око» почти всегда будет преобладать, хотя неприятные стратегии будут приходить в популяцию и уходить от нее, потому что популяция «око за око» проницаема для хороших стратегий, которые, в свою очередь, являются легкой добычей для противных стратегии. Ричард Докинз показал, что здесь никакое статическое сочетание стратегий не формирует устойчивого равновесия, и система всегда будет колебаться между границами.}} эта стратегия в итоге заняла три верхних позиции в соревновании, а также несколько позиций вниз.

Эта стратегия использует тот факт, что в данном конкретном соревновании было разрешено несколько участников, и что производительность команды измерялась по результативности игрока, набравшего наибольшее количество очков (что означает, что использование самоотверженных игроков было формой минимизация ). В соревновании, где под контролем только один игрок, «око за око», безусловно, лучшая стратегия. Из-за этого нового правила это соревнование также имеет мало теоретического значения при анализе стратегий одного агента по сравнению с основополагающим турниром Аксельрода. Тем не менее, это послужило основой для анализа того, как достичь кооперативных стратегий в многоагентных средах, особенно в присутствии шума. Фактически, задолго до того, как состоялся этот турнир по новым правилам, Докинз в своей книге Эгоистичный ген, указал на возможность выигрыша таких стратегий, если бы было разрешено несколько заявок, но он заметил, что, скорее всего, Аксельрод не допустил бы их, если бы они были представлены. Он также основан на обходе правил в отношении дилеммы заключенного в том смысле, что между двумя игроками не разрешается общаться, что, возможно, и сделали программы Саутгемптона с их вводным «танцем из десяти движений», чтобы узнать друг друга; это только подтверждает, насколько ценным может быть общение для изменения баланса игры.

Стохастическая повторная дилемма заключенного

В стохастической итерационной игре «дилемма заключенного» стратегии определяются в терминах «вероятностей сотрудничества».^[18] Во встрече между игроком Икс и игрок Y, Икс Стратегия определяется набором вероятностей п сотрудничества с Y. п является функцией результатов их предыдущих встреч или некоторой их части. Если п является функцией только их самых последних п столкновений, это называется стратегией «памяти и n». Тогда стратегия памяти-1 определяется четырьмя вероятностями сотрудничества: ${\displaystyle P=\{P_{cc},P_{cd},P_{dc},P_{dd}\}}$, куда ${\displaystyle P_{ab}}$ вероятность того, что Икс будет сотрудничать в данной встрече, учитывая, что предыдущая встреча характеризовалась (ab). Например, если в предыдущем столкновении Икс сотрудничал и Y дезертировал, то ${\displaystyle P_{cd}}$ вероятность того, что Икс буду сотрудничать в настоящей встрече. Если каждая из вероятностей равна 1 или 0, стратегия называется детерминированной. Примером детерминированной стратегии является стратегия «око за око», записанная как п= {1,0,1,0}, в котором Икс отвечает как Y сделал в предыдущей встрече. Другой - это выиграть - остаться, проиграть - переключиться стратегия, написанная как п= {1,0,0,1}, в котором Икс отвечает, как и в предыдущем столкновении, если это была «победа» (т.е. cc или dc), но меняет стратегию, если это было проигрыш (например, cd или dd). Было показано, что для любой стратегии памяти-n существует соответствующая стратегия памяти-1, которая дает те же статистические результаты, поэтому необходимо рассматривать только стратегии памяти-1.^[18]

Если мы определим п как приведенный выше 4-элементный вектор стратегии Икс и ${\displaystyle Q=\{Q_{cc},Q_{cd},Q_{dc},Q_{dd}\}}$ как 4-элементный вектор стратегии Y, матрица перехода M может быть определен для Икс чей ij -я запись - это вероятность того, что результат конкретной встречи между Икс и Y будет j учитывая, что предыдущая встреча была я, куда я и j являются одним из четырех показателей результата: cc, CD, Округ Колумбия, или же дд. Например, из Икс с точки зрения США, вероятность того, что исход настоящей встречи CD учитывая, что предыдущая встреча была CD равно ${\displaystyle M_{cd,cd}=P_{cd}(1-Q_{dc})}$. (Индексы для Q из Y точка зрения: a CD результат для Икс это Округ Колумбия результат для Y.) Согласно этим определениям повторная дилемма заключенного квалифицируется как случайный процесс и M это стохастическая матрица, что позволяет применять всю теорию случайных процессов.^[18]

Одним из результатов стохастической теории является то, что существует стационарный вектор v для матрицы M такой, что ${\displaystyle v\cdot M=v}$. Без ограничения общности можно указать, что v нормирован так, что сумма его четырех компонентов равна единице. В ij й вход в ${\displaystyle M^{n}}$ даст вероятность того, что исход встречи между Икс и Y будет j учитывая, что встреча п предыдущие шаги я. В пределе как п приближается к бесконечности, M будет сходиться к матрице с фиксированными значениями, давая долгосрочные вероятности встречи, производящей j который не будет зависеть от я. Другими словами, ряды ${\displaystyle M^{\infty }}$ будут идентичны, давая долгосрочные равновесные вероятности результата повторяющейся дилеммы заключенных без необходимости явно оценивать большое количество взаимодействий. Видно, что v стационарный вектор для ${\displaystyle M^{n}}$ и особенно ${\displaystyle M^{\infty }}$, так что каждая строка ${\displaystyle M^{\infty }}$ будет равно v. Таким образом, стационарный вектор задает вероятности равновесного исхода для Икс. Определение ${\displaystyle S_{x}=\{R,S,T,P\}}$ и ${\displaystyle S_{y}=\{R,T,S,P\}}$ в качестве векторов краткосрочных выплат для результатов {cc, cd, dc, dd} (From Икс точки зрения), равновесные выплаты для Икс и Y теперь можно указать как ${\displaystyle s_{x}=v\cdot S_{x}}$ и ${\displaystyle s_{y}=v\cdot S_{y}}$, позволяя двум стратегиям п и Q чтобы сравнить их долгосрочную отдачу.

Нулевые детерминантные стратегии

Взаимосвязь между стратегиями нулевого детерминанта (ZD), сотрудничества и отказа в повторяющейся дилемме заключенного (IPD), проиллюстрированная в Диаграмма Венна. Стратегии сотрудничества всегда взаимодействуют с другими стратегиями сотрудничества, а стратегии отклонения всегда противоречат другим стратегиям отклонения. Оба содержат подмножества стратегий, которые устойчивы при сильном отборе, что означает, что никакая другая стратегия памяти-1 не выбрана для вторжения в такие стратегии, когда они являются резидентными в популяции.Только взаимодействующие стратегии содержат подмножество, которое всегда устойчиво, что означает, что никакая другая стратегия памяти-1 не выбрана для вторжения и замены таких стратегий как при сильной, так и слабый отбор. Пересечение между ZD и хорошими стратегиями сотрудничества - это набор щедрых ZD-стратегий. Стратегии вымогательства - это пересечение ZD и ненадежных дефектных стратегий. «Око за око» лежит на пересечении стратегий сотрудничества, отказа и ZD.

В 2012, Уильям Х. Пресс и Фриман Дайсон опубликовал новый класс стратегий для стохастической повторной дилеммы заключенного, названный стратегиями с нулевым определением (ZD).^[18] Долгосрочная отдача от встреч между Икс и Y может быть выражен как определитель матрицы, которая является функцией двух стратегий и векторов краткосрочных выплат: ${\displaystyle s_{x}=D(P,Q,S_{x})}$ и ${\displaystyle s_{y}=D(P,Q,S_{y})}$, в которых не участвует стационарный вектор v. Поскольку детерминантная функция ${\displaystyle s_{y}=D(P,Q,f)}$ линейно по ж, следует, что ${\displaystyle \alpha s_{x}+\beta s_{y}+\gamma =D(P,Q,\alpha S_{x}+\beta S_{y}+\gamma U)}$ (куда U= {1,1,1,1}). Любые стратегии, для которых ${\displaystyle D(P,Q,\alpha S_{x}+\beta S_{y}+\gamma U)=0}$ по определению является ZD-стратегией, а долгосрочные выплаты подчиняются соотношению ${\displaystyle \alpha s_{x}+\beta s_{y}+\gamma =0}$.

«Око за око» - это стратегия ZD, которая «справедлива» в том смысле, что не получает преимущества над другим игроком. Тем не менее, пространство ZD также содержит стратегии, которые в случае двух игроков могут позволить одному игроку в одностороннем порядке установить счет другого игрока или, в качестве альтернативы, заставить эволюционного игрока достичь выигрыша на несколько процентов ниже, чем его собственный. Вымогаемый игрок может дезертировать, но тем самым причинит себе вред, получив меньший выигрыш. Таким образом, решения о вымогательстве превращают повторяющуюся дилемму заключенного в своего рода ультиматумная игра. Конкретно, Икс может выбрать стратегию, для которой ${\displaystyle D(P,Q,\beta S_{y}+\gamma U)=0}$, в одностороннем порядке устанавливающий ${\displaystyle s_{y}}$ к определенному значению в определенном диапазоне значений, независимо от Y стратегия, предлагающая возможность Икс "вымогать" игрока Y (наоборот). (Получается, что если Икс пытается установить ${\displaystyle s_{x}}$ Для конкретного значения диапазон возможностей намного меньше, они состоят только из полного сотрудничества или полного отступничества.^[18])

Расширением IPD является эволюционный стохастический IPD, в котором относительное количество конкретных стратегий может изменяться, при этом более успешные стратегии относительно увеличиваются. Этот процесс может быть осуществлен за счет того, что менее успешные игроки имитируют более успешные стратегии или путем исключения менее успешных игроков из игры при умножении более успешных. Было показано, что несправедливые стратегии ZD не эволюционно стабильный. Ключевая интуиция состоит в том, что эволюционно стабильная стратегия должна не только иметь возможность вторгаться в другую популяцию (что могут делать вымогательные стратегии ZD), но также должна хорошо работать против других игроков того же типа (какие игроки-вымогатели ZD делают плохо, потому что они уменьшают каждый чужой излишек).^[19]

Теория и моделирование подтверждают, что за пределами критического размера популяции ZD-вымогательство проигрывает в эволюционной конкуренции с более кооперативными стратегиями, и в результате средний выигрыш в популяции увеличивается, когда популяция становится больше. Кроме того, в некоторых случаях вымогатели могут даже стимулировать сотрудничество, помогая вырваться из столкновения между унифицированными перебежчиками и выиграть - остаться, проиграть - переключиться агенты.^[11]

В то время как вымогательские стратегии ZD нестабильны в больших популяциях, другой класс ZD называется «щедрые» стратегии является и стабильный, и надежный. Фактически, когда популяция не слишком мала, эти стратегии могут вытеснить любую другую стратегию ZD и даже хорошо работать с широким набором общих стратегий для повторяющейся дилеммы заключенного, в том числе «победить - остаться, проиграть - переключиться». Это было доказано специально для игра с пожертвованиями Александра Стюарта и Джошуа Плоткина в 2013 году.^[20] Щедрые стратегии будут сотрудничать с другими кооперативными игроками, и перед лицом отступничества щедрый игрок теряет больше полезности, чем его соперник. Щедрые стратегии - это пересечение стратегий ZD и так называемых «хороших» стратегий, которые были определены Akin (2013).^[21] быть теми, для которых игрок отвечает на прошлое взаимное сотрудничество будущим сотрудничеством и делит ожидаемые выплаты поровну, если он получает, по крайней мере, ожидаемую кооперативную выплату. Среди хороших стратегий подмножество щедрых (ZD) хорошо работает, когда популяция не слишком мала. Если популяция очень мала, преобладают стратегии дезертирства.^[20]

Непрерывная повторяющаяся дилемма заключенного

Большая часть работ по повторной дилемме заключенного сосредоточена на дискретном случае, в котором игроки либо сотрудничают, либо отступают, потому что эту модель относительно просто анализировать. Тем не менее, некоторые исследователи рассмотрели модели постоянно повторяющейся дилеммы заключенного, в которой игроки могут вносить переменный вклад в пользу другого игрока. Ле и Бойд^[22] обнаружили, что в таких ситуациях развивать сотрудничество гораздо труднее, чем в дискретной повторяющейся дилемме заключенного. Основная интуиция для этого результата проста: в постоянной дилемме заключенного, если популяция начинается в некооперативном равновесии, игроки, которые лишь незначительно более склонны к сотрудничеству, чем не сотрудничающие, получают небольшую выгоду от сортировка друг с другом. Напротив, в дилемме дискретного заключенного, кооператоры «око за око» получают большую выгоду от сортировки друг с другом в некооперативном равновесии по сравнению с теми, кто не сотрудничает. Поскольку природа, возможно, предлагает больше возможностей для разнообразного сотрудничества, а не строгой дихотомии сотрудничества или отступничества, постоянная дилемма заключенного может помочь объяснить, почему реальные примеры сотрудничества, похожего на око за око, чрезвычайно редки в природе (например, Хаммерштейн^[23]), хотя в теоретических моделях кажется устойчивым.

Появление стабильных стратегий

Кажется, что игроки не могут координировать взаимное сотрудничество, поэтому часто попадают в низшую, но стабильную стратегию отступничества. Таким образом, повторяющиеся раунды способствуют развитию стабильных стратегий.^[24] Повторяющиеся раунды часто приводят к новым стратегиям, которые имеют значение для сложного социального взаимодействия. Одна из таких стратегий - выиграть-остаться-проиграть-сдвиг. Эта стратегия превосходит простую стратегию «око за око» - то есть, если вам удается избежать мошенничества, повторите это поведение, однако, если вас поймают, переключитесь.^[25]

Единственная проблема этой стратегии «око за око» состоит в том, что они уязвимы для ошибки сигнала. Проблема возникает, когда один человек обманывает в отместку, а другой интерпретирует это как обман. В результате второй человек теперь обманывает, а затем начинает цепную реакцию обмануть по схеме качелей.

Примеры из реальной жизни

Обстановка заключенного может показаться надуманной, но на самом деле существует множество примеров человеческого взаимодействия, а также взаимодействия в природе, которые имеют одинаковую матрицу выигрыша. Таким образом, дилемма заключенного представляет интерес для социальные науки Такие как экономика, политика, и социология, а также в биологических науках, таких как этология и эволюционная биология. Многие естественные процессы были абстрагированы в модели, в которых живые существа участвуют в бесконечных играх с дилеммой заключенного. Такая широкая применимость PD придает игре большое значение.

Экологические исследования

В экологические исследования, PD проявляется в кризисах, таких как глобальные изменение климата. Утверждается, что от стабильного климата выиграют все страны, но любая отдельная страна часто не решается ограничить CO
2 выбросы. Непосредственная выгода для любой страны от сохранения текущего поведения ошибочно воспринимается как большая, чем предполагаемая конечная выгода для этой страны, если поведение всех стран изменится, что объясняет тупик, связанный с изменением климата в 2007 году.^[26]

Важное различие между политикой в ​​области изменения климата и дилеммой заключенного - неопределенность; степень и скорость, с которой загрязнение может изменить климат, неизвестны. Таким образом, дилемма, стоящая перед правительством, отличается от дилеммы заключенного тем, что отдача от сотрудничества неизвестна. Это различие предполагает, что государства будут сотрудничать в гораздо меньшей степени, чем в реальной повторяющейся дилемме заключенного, поэтому вероятность избежать возможной климатической катастрофы намного меньше, чем предполагает теоретико-игровой анализ ситуации с использованием реальной повторяющейся дилеммы заключенного.^[27]

Осанг и Нанди (2003) предоставляют теоретическое объяснение с доказательствами беспроигрышной ситуации, основанной на регулировании, в духе Майкл Портер Гипотеза, в которой государственное регулирование конкурирующих фирм является существенным.^[28]

Животные

Кооперативное поведение многих животных можно рассматривать как пример дилеммы заключенного. Часто животные вступают в долгосрочные партнерские отношения, что более конкретно можно смоделировать как повторяющуюся дилемму заключенного. Например, гуппи совместно инспектируют хищников группами, и считается, что они наказывают инспекторов, отказывающихся сотрудничать.

Летучие мыши-вампиры социальные животные, которые участвуют во взаимном обмене пищей. Объяснить такое поведение можно, применяя выплаты из дилеммы заключенного:^[29]

• C / C: «Награда: в мои неудачные ночи я проливаю кровь, что спасает меня от голода. Я должен сдавать кровь в мои счастливые ночи, что мне не стоит слишком дорого».
• D / C: «Искушение: вы спасли мою жизнь в мою плохую ночь. Но тогда я получаю дополнительное преимущество, так как мне не нужно платить небольшую стоимость кормления вас в мою спокойную ночь».
• C / D: «Выплата присоски: я плачу за спасение вашей жизни в мою спокойную ночь. Но в мою плохую ночь вы не кормите меня, и я рискую умереть от голода».
• Д / Д: «Наказание: мне не нужно оплачивать небольшие расходы на то, чтобы кормить вас в мои спокойные ночи. Но я рискую умереть с голоду в свои плохие ночи».

Психология

В зависимость исследование / поведенческая экономика, Джордж Эйнсли указывает на то^[30] эту зависимость можно представить как межвременную проблему БП между настоящим и будущим «я» наркомана. В этом случае, дезертирство средства рецидивирующий, и легко видеть, что отказ от дезертирства ни сегодня, ни в будущем - лучший результат. Случай, когда человек воздерживается сегодня, но возвращается в будущем, является худшим исходом - в некотором смысле дисциплина и самопожертвование, связанные с воздержанием сегодня, были «потрачены впустую», потому что будущий рецидив означает, что наркоман вернулся туда, откуда он начал, и будет приходится начинать заново (что довольно деморализует и затрудняет начало работы). Рецидив сегодня и завтра - это немного «лучший» результат, потому что, хотя наркоман все еще остается зависимым, он не прилагает усилий, чтобы попытаться остановиться. Последний случай, когда человек проявляет аддиктивное поведение сегодня, воздерживаясь от «завтра», будет знаком каждому, кто боролся с зависимостью. Проблема здесь в том, что (как и в других ВД) существует очевидная выгода от отказа «сегодня», но завтра вы столкнетесь с тем же самым ВД, и тогда будет присутствовать такая же очевидная выгода, что в конечном итоге приведет к бесконечной череде отступников.

Джон Готтман в своем исследовании, описанном в «науке о доверии», он определяет хорошие отношения как отношения, в которых партнеры знают, что они не должны входить в ячейку (D, D) или, по крайней мере, не застревать там в цикле.

Экономика

Дилемму заключенного назвали Кишечная палочка социальной психологии, и он широко использовался для исследования различных тем, таких как олигополистический конкуренция и коллективные действия для производства коллективного блага.^[31]

Рекламу иногда приводят как реальный пример дилеммы заключенного. Когда реклама сигарет было законным в Соединенных Штатах, конкурирующие производители сигарет должны были решить, сколько денег потратить на рекламу. Эффективность рекламы фирмы A частично определялась рекламой, проводимой фирмой B. Аналогичным образом, прибыль, полученная от рекламы для фирмы B, зависит от рекламы, проводимой фирмой A. Если и фирма A, и фирма B решили размещать рекламу в течение заданного периода времени. периода, то реклама одной фирмы отрицает рекламу другой, поступления остаются неизменными, а расходы увеличиваются из-за стоимости рекламы. Обе фирмы выиграют от сокращения рекламы. Однако, если фирма B решит не размещать рекламу, она может получить большую выгоду от рекламы. Тем не менее, оптимальный объем рекламы одной фирмы зависит от того, сколько рекламы берет на себя другая. Поскольку лучшая стратегия зависит от того, что выберет другая фирма, доминирующей стратегии нет, что немного отличает ее от дилеммы заключенного. Однако результат схож: обеим фирмам было бы лучше, если бы они рекламировали меньше, чем в состоянии равновесия. Иногда в деловых ситуациях проявляется кооперативное поведение. Например, производители сигарет одобрили принятие законов, запрещающих рекламу сигарет, понимая, что это снизит затраты и увеличит прибыль во всей отрасли.^{[нужна цитата ][b]} Этот анализ, вероятно, будет уместен во многих других бизнес-ситуациях, связанных с рекламой.^{[нужна цитата ]}

Без обязательных соглашений члены картель также вовлечены в дилемму заключенного (многопользовательской).^[32] «Сотрудничество» обычно означает поддержание цен на заранее согласованном минимальном уровне. «Отклонение от ответственности» означает продажу ниже этого минимального уровня, мгновенно отнимая бизнес (и прибыль) у других членов картеля. Антимонопольный власти хотят, чтобы потенциальные участники картеля взаимно дезертировали, обеспечивая минимально возможные цены на потребители.

Спорт

Допинг в спорте приводился как пример дилеммы заключенного.^[33]

Два соревнующихся спортсмена имеют возможность использовать запрещенные и / или опасные препараты для повышения своих результатов. Если ни один из спортсменов не принимает препарат, ни один из них не получает преимущества. Если это сделает только один, то этот спортсмен получает значительное преимущество перед своим конкурентом, уменьшенное за счет юридических и / или медицинских опасностей, связанных с приемом препарата. Однако, если оба спортсмена принимают препарат, преимущества отменяются, и остаются только опасности, что ставит их обоих в худшее положение, чем если бы ни один из них не принимал допинг.^[33]

Международная политика

В международная политическая теория, дилемма заключенного часто используется для демонстрации согласованности стратегический реализм, который утверждает, что в международных отношениях все государства (независимо от их внутренней политики или исповедуемой идеологии) будут действовать в своих рациональных личных интересах с учетом международная анархия. Классический пример - гонка вооружений, подобная Холодная война и подобные конфликты.^[34] Во время холодной войны противоборствующие союзы НАТО и Варшавский договор у обоих был выбор: поставить или разоружить. С точки зрения каждой стороны, разоружение, пока их противник продолжал вооружаться, привело бы к военному проигрышу и возможному уничтожению. И наоборот, вооружение, пока их противник разоружен, привело бы к превосходству. Если обе стороны захотят вооружиться, ни одна из них не сможет позволить себе атаковать другую, но обе несут высокие затраты на создание и поддержание ядерного арсенала. Если обе стороны решат разоружиться, войны можно будет избежать и никаких затрат не будет.

Хотя «лучший» общий результат - разоружение для обеих сторон, рациональный курс для обеих сторон - вооружиться, и именно это действительно произошло. Обе стороны вложили огромные ресурсы в военные исследования и вооружения в война на истощение в течение следующих тридцати лет, пока Советский Союз не выдержал экономических издержек.^[35] Та же логика может применяться в любом подобном сценарии, будь то экономическая или технологическая конкуренция между суверенными государствами.

Дилеммы многопользовательской игры

Многие дилеммы реальной жизни связаны с несколькими игроками.^[36] Хотя метафорически, Хардин Трагедия общественного достояния можно рассматривать как пример многопользовательского обобщения ПД: каждый сельский житель делает выбор в пользу личной выгоды или сдержанности. Коллективная награда за единодушное (или даже частое) дезертирство - очень низкие выплаты (представляющие собой уничтожение «общего достояния»). Дилемма общего пользования, с которой может столкнуться большинство людей, - это мытье посуды в общем доме. Отказавшись от мытья посуды, человек может сэкономить свое время, но если это поведение будет принято каждым жителем, коллективные издержки - это не чистые тарелки для кого-либо.

Общественное достояние не всегда используется: Уильям Паундстон в книге о дилемме заключенного описывает ситуацию в Новой Зеландии, где газетные ящики остаются незапертыми. Люди могут взять бумагу без оплаты (дезертирство), но очень немногие делают это, чувствуя, что если они не платят, то и другие не будут платить, разрушая систему.^[37] Последующие исследования Элинор Остром, победитель 2009 г. Нобелевская мемориальная премия по экономическим наукам, выдвинул гипотезу о том, что трагедия общества чрезмерно упрощена, а отрицательный результат зависит от внешних влияний. Не усложняя давление, группы общаются и управляют обществом между собой для их взаимной выгоды, обеспечивая соблюдение социальных норм для сохранения ресурса и достижения максимальной пользы для группы, что является примером достижения наилучшего результата для PD.^[38][39]

Связанные игры

Обмен закрытых сумок

Дилемма заключенного как обмен портфелем

Дуглас Хофштадтер^[40] однажды предположил, что люди часто находят проблемы, такие как проблема частичного разряда, более понятными, когда она проиллюстрирована в форме простой игры или компромисса. Одним из нескольких примеров, которые он использовал, был «закрытый обмен сумок»:

Два человека встречаются и обмениваются закрытыми мешками, при этом понимая, что в одном из них лежат деньги, а в другом - покупка. Любой игрок может выполнить сделку, положив в свою сумку то, что он или она согласился, или он или она может отказаться, передав пустой мешок.

Дефект всегда дает теоретически более предпочтительный исход.^[41]

Друг или враг?

Друг или враг? это игровое шоу, которое транслировалось с 2002 по 2003 год на Сеть игровых шоу в США. Это пример игры-дилеммы заключенного, проверенной на реальных людях, но в искусственной обстановке. В игровом шоу соревнуются три пары людей. Когда пара выбывает, они играют в игру, похожую на дилемму заключенного, чтобы определить, как делится выигрыш. Если они оба сотрудничают (Друг), они делят выигрыш 50–50. Если один сотрудничает, а другой отказывает (Враг), перебежчик получает весь выигрыш, а кооператор ничего не получает. Если оба неисправны, оба уходят ни с чем. Обратите внимание, что матрица вознаграждений немного отличается от стандартной, приведенной выше, поскольку вознаграждения в случаях «оба дефекта» и «сотрудничать, пока оппонент ошибается» идентичны. Это делает случай «оба дефекта» слабым равновесием по сравнению со строгим равновесием в стандартной дилемме заключенного. Если участник знает, что его противник проголосует «за врага», то его собственный выбор не влияет на его собственный выигрыш. В определенном смысле Друг или враг есть модель вознаграждения между дилеммой заключенного и игра в курицу.

Матрица вознаграждений:

Пара 2 Пара 1	"Друг" (сотрудничать)	"Враг" (дефект)
"Друг" (сотрудничать)	1 1	2 0
"Враг" (дефект)	0 2	0 0

Эта матрица выплат также использовалась для Британский телевидение программы Поверьте мне, Shafted, Работа в банке и Золотые шары, и на Американец игра показывает Возьми все, а также для победившей пары на реалити-шоу Холостяк. Игровые данные из Золотые шары серия была проанализирована группой экономистов, которые обнаружили, что сотрудничество было «на удивление высоким» для сумм денег, которые могли бы иметь важное значение в реальном мире, но были сравнительно низкими в контексте игры.^[42]

Итерированный сугроб

Основная статья: игра в сугроб

Исследователи из Университет Лозанны и Эдинбургский университет предположили, что «Итерационная игра в снежный занос» может более точно отражать реальные социальные ситуации. Хотя эта модель на самом деле куриная игра, это будет описано здесь. В этой модели риск эксплуатации через дезертирство ниже, и люди всегда выигрывают от совместного выбора. Игра в сугроб представляет двух водителей, застрявших по разные стороны дороги. сугроб, каждый из которых может убрать снег, чтобы расчистить дорогу, или остаться в машине. Самый высокий выигрыш для игрока - это то, что он оставляет соперника самому убирать снег, но противник все равно номинально награждается за свою работу.

Это может лучше отражать сценарии реального мира: исследователи приводят пример двух ученых, сотрудничающих над отчетом, и оба выиграют, если другой будет работать усерднее. «Но когда ваш соавтор не выполняет никакой работы, вероятно, вам лучше сделать всю работу самостоятельно. У вас все равно будет завершенный проект».^[43]

Пример выплаты сугроба (A, B) B А Сотрудничает Дефекты Сотрудничает 200, 200 100, 300 Дефекты 300, 100 0, 0

Пример выплат PD (A, B) B А Сотрудничает Дефекты Сотрудничает 200, 200 -100, 300 Дефекты 300, -100 0, 0

Координационные игры

Основная статья: координационные игры

В координационных играх игроки должны координировать свои стратегии для достижения хорошего результата. Пример - две машины, которые резко встречаются в метель; каждый должен выбрать, свернуть влево или вправо. Если оба повернут налево или оба повернут направо, машины не столкнутся. Местный левостороннее и правостороннее движение условность помогает координировать свои действия.

Симметричные координационные игры включают: Охота на оленя и Бах или Стравинский.

Асимметричные дилеммы заключенного

Более общий набор игр асимметричен. Как и в случае с дилеммой заключенного, лучший выход - это сотрудничество, и для отступничества есть мотивы. Однако, в отличие от дилеммы симметричного заключенного, один игрок может больше потерять и / или больше получить, чем другой. Некоторые такие игры были описаны как дилемма заключенного, в которой один заключенный алиби Отсюда и термин «алиби-игра».^[44]

В экспериментах игроки, получающие неравные выплаты в повторяющихся играх, могут стремиться к максимизации прибыли, но только при условии, что оба игрока получают равные выплаты; это может привести к стратегии стабильного равновесия, в которой проигравший игрок отказывается от всех X игр, в то время как другой всегда сотрудничает. Такое поведение может зависеть от социальных норм эксперимента в отношении справедливости.^[45]

Программного обеспечения

Было создано несколько программных пакетов для моделирования дилемм заключенного и проведения турниров, некоторые из которых имеют доступный исходный код.

• Исходный код для второй турнир под управлением Роберта Аксельрода (написано Аксельродом и многими участниками в Фортран ) доступен онлайн
• Тюрьма, библиотека, написанная на Ява, последнее обновление в 1998 г.
• Аксельрод-Питон, написано в Python
• играть в Итеративную дилемму заключенного в браузере, играйте против стратегий или позволяйте стратегиям играть против других стратегий

В художественной литературе

Ханну Раджаниеми установить начальную сцену его Квантовый вор трилогия в «тюрьме дилеммы». Основная тема сериала описывается как «неадекватность бинарной вселенной», а главный антагонист - персонаж по имени Все-Перебежчик. Раджаниеми особенно интересен как художник, занимающийся этим предметом, поскольку он математик, получивший образование в Кембридже, и имеет докторскую степень в области математики. математическая физика - взаимозаменяемость материи и информации - главная особенность книг, действие которой происходит в «постсингулярном» будущем. Первая книга серии вышла в 2010 году с двумя продолжениями: Фрактальный принц и Причинный ангел, опубликованные в 2012 и 2014 годах соответственно.

Игра, созданная по образцу (повторной) дилеммы заключенного, является центральной темой видеоигры 2012 года. Zero Escape: последняя награда добродетели и второстепенная роль в его продолжении 2016 года Zero Escape: дилемма нулевого времени.

В Таинственное общество Бенедикта и дилемма заключенного к Трентон Ли Стюарт, главные герои начинают с того, что играют в одну из версий игры и вообще сбегают из «тюрьмы». Позже они становятся настоящими заключенными и снова сбегают.

В Зона приключений: Баланс в течение Страдающая игра subarc, игровые персонажи дважды сталкиваются с дилеммой заключенного за время их пребывания в владениях двух личей: один раз сотрудничают, а другой - дезертируют.

В 8-м романе автора Джеймса С. А. Кори Гнев Тиамат, Уинстон Дуарте объясняет дилемму заключенных своей 14-летней дочери Терезе, чтобы научить ее стратегическому мышлению.^{[нужна цитата ]}

Об этом буквально говорится в фильме 2019 года. Платформа, где заключенные в вертикальной тюрьме могут есть только то, что осталось от вышестоящих. Если бы каждый ел свою справедливую долю, еды было бы достаточно, но показано, что те, кто находится на нижних уровнях, голодают из-за чрезмерного потребления заключенных.

Смотрите также

• Парадокс Абилина
• Сороконожка игра
• Рождественское перемирие
• Внешность
• Народная теорема (теория игр)
• Проблема безбилетника
• Гоббсовская ловушка
• Дилемма невинного заключенного
• Лжец Игра
• Необязательная дилемма заключенного
• Дилемма заключенного и сотрудничество
• Игра в общественные блага
• Игра по обмену подарками
• Взаимный альтруизм
• Поиск аренды
• Социальные предпочтения
• Теория быстрого доверия
• Дилемма недобросовестного посетителя

Рекомендации

1. Например, см. Исследование 2003 г.^[15] для обсуждения концепции и возможности ее применения на практике экономический или стратегические ситуации.
2. Этот аргумент в пользу развития сотрудничества через доверие приводится в Мудрость толпы, где утверждается, что междугородные капитализм смог сформироваться вокруг ядра Квакеры, которые всегда честно относились к своим деловым партнерам. (Вместо того, чтобы отказываться от обещаний и не выполнять обещания - явление, которое препятствовало заключению ранее заключенных долгосрочных невыполнимых зарубежных контрактов). Утверждается, что отношения с надежными торговцами позволили мем чтобы сотрудничество распространялось на других трейдеров, которые распространяли его дальше, пока высокая степень сотрудничества не стала прибыльной стратегией в целом коммерция

1. Паундстон 1993 С. 8, 117.
2. Миловский, Николай. «Основы теории игр и связанных игр». Получено 11 февраля 2014.
3. Фер, Эрнст; Фишбахер, Урс (23 октября 2003 г.). «Природа человеческого альтруизма» (PDF). Природа. 425 (6960): 785–91. Bibcode:2003Натура.425..785F. Дои:10.1038 / природа02043. PMID  14574401. S2CID  4305295. Получено 27 февраля, 2013.
4. Тверски, Амос; Шафир, Эльдар (2004). Предпочтение, вера и сходство: избранные произведения (PDF). Массачусетский технологический институт Press. ISBN  9780262700931. Получено 27 февраля, 2013.
5. Toh-Kyeong, Ан; Остром, Элинор; Уокер, Джеймс (5 сентября 2002 г.). «Включение мотивационной неоднородности в теоретико-игровые модели коллективных действий» (PDF). Общественный выбор. 117 (3–4): 295–314. Дои:10.1023 / б: пуч.0000003739.54365.fd. HDL:10535/4697. S2CID  153414274. Получено 27 июня, 2015.
6. Oosterbeek, Hessel; Sloof, Рэндольф; Ван де Куилен, Гас (3 декабря 2003 г.). «Культурные различия в ультимативных игровых экспериментах: данные метаанализа» (PDF). Экспериментальная экономика. 7 (2): 171–88. Дои:10.1023 / B: EXEC.0000026978.14316.74. S2CID  17659329. Архивировано из оригинал (PDF) 12 мая 2013 г.. Получено 27 февраля, 2013.
7. Ормерод, Пол (22 декабря 2010 г.). Почему большинство вещей терпят неудачу. ISBN  9780571266142.
8. Дойч, М. (1958). Доверие и подозрение. Журнал разрешения конфликтов, 2 (4), 265–279. https://doi.org/10.1177/002200275800200401
9. Рапопорт, А., Чамма, А.М. (1965). Дилемма заключенного: исследование конфликта и сотрудничества. Анн-Арбор, Мичиган: Издательство Мичиганского университета.
10. Казначеев, Артем (2 марта 2015 г.). "Краткая история повторяющихся турниров по дилемме заключенного". Группа теории, эволюции и игр. Получено 8 февраля, 2016.
11. Хильбе, Кристиан; Мартин А. Новак; Карл Зигмунд (апрель 2013 г.). «Эволюция вымогательства в повторяющихся играх« Дилемма заключенного »». PNAS. 110 (17): 6913–18. arXiv:1212.1067. Bibcode:2013PNAS..110.6913H. Дои:10.1073 / pnas.1214834110. ЧВК  3637695. PMID  23572576.
12. Застенчивая, Оз (1995). Промышленная организация: теория и приложения. Массачусетский технологический институт Press. ISBN  978-0262193665. Получено 27 февраля, 2013.
13. Даль Бо, Педро; Фрешет, Гийом Р. (2019). «Выбор стратегии в бесконечно повторяющейся дилемме заключенного». Американский экономический обзор. 109 (11): 3929–3952. Дои:10.1257 / aer.20181480. ISSN  0002-8282.
14. Wedekind, C .; Милински, М. (2 апреля 1996 г.). «Человеческое сотрудничество в одновременной и альтернативной дилемме заключенного: Павлов против щедрого око за око». Труды Национальной академии наук. 93 (7): 2686–2689. Дои:10.1073 / pnas.93.7.2686. ЧВК  39691. PMID  11607644.
15. «Байесовское равновесие по Нэшу; статистическая проверка гипотезы» (PDF). Тель-авивский университет. Архивировано из оригинал (PDF) на 2005-10-02.
16. Ву, Цзядон; Чжао, Чэнъе (2019), Сунь, Сяомин; Он, Кун; Чен, Сяоюнь (ред.), "Сотрудничество по правилу Монте-Карло: игра с дилеммой заключенного в сетке", Теоретическая информатика, Springer Singapore, 1069, стр. 3–15, Дои:10.1007/978-981-15-0105-0_1, ISBN  978-981-15-0104-3, S2CID  118687103
17. «Команда Саутгемптонского университета выиграла соревнование« Дилемма заключенного »» (Пресс-релиз). Саутгемптонский университет. 7 октября 2004 г. Архивировано с оригинал на 2014-04-21.
18. Нажмите, WH; Дайсон, Ф.Дж. (26 июня 2012 г.). «Повторяющаяся дилемма заключенного содержит стратегии, которые доминируют над любым эволюционным противником». Труды Национальной академии наук Соединенных Штатов Америки. 109 (26): 10409–13. Bibcode:2012PNAS..10910409P. Дои:10.1073 / pnas.1206569109. ЧВК  3387070. PMID  22615375.
19. Адами, Кристоф; Аренд Хинтце (2013). «Эволюционная нестабильность стратегий нулевого детерминанта показывает, что победа - это еще не все». Nature Communications. 4: 3. arXiv:1208.2666. Bibcode:2013 НатКо ... 4.2193A. Дои:10.1038 / ncomms3193. ЧВК  3741637. PMID  23903782.
20. Стюарт, Александр Дж .; Джошуа Б. Плоткин (2013). «От вымогательства к щедрости - эволюция в повторяющейся дилемме заключенного». Труды Национальной академии наук Соединенных Штатов Америки. 110 (38): 15348–53. Bibcode:2013ПНАС..11015348С. Дои:10.1073 / пнас.1306246110. ЧВК  3780848. PMID  24003115.
21. Акин, Итан (2013). «Стабильные совместные решения для повторяющейся дилеммы заключенного». п. 9. arXiv:1211.0969 [math.DS ]. Bibcode:2012arXiv1211.0969A
22. Ле С., Бойд Р. (2007). "Эволюционная динамика непрерывной повторяющейся дилеммы заключенного". Журнал теоретической биологии. 245 (2): 258–67. Дои:10.1016 / j.jtbi.2006.09.016. PMID  17125798.
23. Хаммерштейн, П. (2003). Почему взаимность так редко встречается у социальных животных? Протестантское обращение. В: П. Хаммерштейн, редактор отдела генетической и культурной эволюции сотрудничества, MIT Press. С. 83–94.
24. Спаниель, Уильям (2011). Теория игр 101: Полный учебник.
25. Новак, Мартин; Карл Зигмунд (1993). «Стратегия взаимовыгодного пребывания, проигрыша-сдвига, которая превосходит« око за око »в игре« Дилемма заключенного ». Природа. 364 (6432): 56–58. Bibcode:1993Натура.364 ... 56Н. Дои:10.1038 / 364056a0. PMID  8316296. S2CID  4238908.
26. «Рынки и данные». Экономист. 2007-09-27.
27. Рехмейер, Джули (2012-10-29). «Теория игр предполагает, что нынешние переговоры по климату не предотвратят катастрофу». Новости науки. Общество науки и общественности.
28. Осанг, Томас; Нандиз, Арундати (август 2003 г.). Экологическое регулирование предприятий, загрязняющих окружающую среду: пересмотр гипотезы Портера (PDF) (бумага).
29. Докинз, Ричард (1976). Эгоистичный ген. Издательство Оксфордского университета.
30. Эйнсли, Джордж (2001). Нарушение воли. ISBN  978-0-521-59694-7.
31. Аксельрод, Роберт (1980). «Эффективный выбор в дилемме заключенного». Журнал разрешения конфликтов. 24 (1): 3–25. Дои:10.1177/002200278002400101. ISSN  0022-0027. JSTOR  173932. S2CID  143112198.
32. Николсон, Уолтер (2000). Промежуточная микроэкономика и ее применение (8-е изд.). Форт-Уэрт, Техас: Dryden Press: Harcourt College Publishers. ISBN  978-0-030-25916-6.
33. Шнайер, Брюс (2012-10-26). "Лэнс Армстронг и дилемма заключенных относительно допинга в профессиональном спорте | Wired Opinion". Проводной. Wired.com. Получено 2012-10-29.
34. Стивен Дж. Майески (1984). «Гонка вооружений как повторяющиеся игры дилеммы заключенного». Математические и социальные науки. 7 (3): 253–66. Дои:10.1016/0165-4896(84)90022-2.
35. Кун, Стивен (2019), "Дилемма заключенного", в Залте, Эдвард Н. (ред.), Стэнфордская энциклопедия философии (Зима 2019 г.), Лаборатория метафизических исследований, Стэнфордский университет, получено 2020-04-12
36. Гохале К.С., Траулсен А. Эволюционные игры в мультивселенной. Труды Национальной академии наук. 2010 г. 23 марта. 107 (12): 5500–04.
37. Паундстон 1993 С. 126–127.
38. "Волохский заговор" Элинор Остром и трагедия общин ". Volokh.com. 2009-10-12. Получено 2011-12-17.
39. Остром, Элинор (2015) [1990]. Управление общин: эволюция институтов коллективных действий. Издательство Кембриджского университета. Дои:10.1017 / CBO9781316423936. ISBN  978-1-107-56978-2.
40. Хофштадтер, Дуглас Р. (1985). "Глава 29 Компьютерные турниры "Дилемма заключенного" и эволюция сотрудничества.". Метамагические темы: поиск сущности разума и паттернов. Группа пабов Bantam Dell. ISBN  978-0-465-04566-2.
41. «Дилемма заключенного - Википедия, бесплатная энциклопедия». users.auth.gr. Получено 2020-04-12.
42. Ван ден Ассем, Мартин Дж. (Январь 2012 г.). «Разделить или украсть? Совместное поведение при больших ставках». Наука управления. 58 (1): 2–20. Дои:10.1287 / mnsc.1110.1413. S2CID  1371739. SSRN  1592456.
43. Кюммерли, Рольф. "'Игра Snowdrift возглавляет «Дилемму заключенного» в объяснении сотрудничества ». Получено 11 апреля 2012.
44. Робинсон, Д.Р .; Гофорт, Д.Дж. (5 мая 2004 г.). Игры алиби: дилеммы асимметричного узника (PDF). Заседания Канадской экономической ассоциации, Торонто, 4-6 июня 2004 г.
45. Бекенкамп, Мартин; Хенниг-Шмидт, Хайке; Майер-Риго, Франк П. (4 марта 2007 г.). «Сотрудничество в симметричных и асимметричных играх с дилеммой заключенного» (PDF). Институт Макса Планка по исследованию коллективных благ.

дальнейшее чтение

• Амаде, С. (2016). "Дилемма заключенного", Узники разума. Издательство Кембриджского университета, NY, стр. 24–61.
• Ауманн, Роберт (1959). «Приемлемые баллы в общем кооперативном п-личностные игры ". В Люс, Р. Д.; Такер, А. У. (ред.). Вклад в теорию 23 игр IV. Летопись математики. 40. Принстон, штат Нью-Джерси: Издательство Принстонского университета. С. 287–324. МИСТЕР  0104521.
• Аксельрод, Р. (1984). Эволюция сотрудничества. ISBN  0-465-02121-2
• Биккьери, Кристина (1993). Рациональность и координация. Издательство Кембриджского университета.
• Шахматы, Дэвид М. (декабрь 1988 г.). «Моделирование эволюции поведения: повторяющаяся дилемма заключенных» (PDF). Сложные системы. 2 (6): 663–70.
• Дрешер, М. (1961). Математика стратегических игр: теория и приложения Prentice-Hall, Энглвуд Клиффс, Нью-Джерси.
• Грейф, А. (2006). Институты и путь к современной экономике: уроки средневековой торговли. Издательство Кембриджского университета, Кембридж, ВЕЛИКОБРИТАНИЯ.
• Копельман, Ширли (февраль 2020 г.). «Око за око и не только: легендарное произведение Анатолия Рапопорта». Исследования в области переговоров и управления конфликтами. 13 (1): 60–84. Дои:10.1111 / нсм. 12172.
• Паундстон, Уильям (1993). Дилемма заключенного (1-е изд. Якорных книг). Нью-Йорк: Якорь. ISBN  0-385-41580-X.
• Рапопорт, Анатолий и Альберт М. Чамма (1965). Дилемма заключенного. Пресса Мичиганского университета.

внешняя ссылка

• СМИ, связанные с Дилемма заключенного в Wikimedia Commons
• Дилемма заключенного (Стэнфордская энциклопедия философии)
• Дилемма шалашника Дилемма заключенного в орнитологии - математический мультфильм Ларри Гоника.
• Дилемма заключенного Дилемма заключенного с минифигурками Lego.
• Диксит, Авинаш; Налебафф, Барри (2008). "Дилемма заключенного". В Дэвид Р. Хендерсон (ред.). Краткая энциклопедия экономики (2-е изд.). Индианаполис: Библиотека экономики и свободы. ISBN  978-0865976658. OCLC  237794267.
• Теория игр 101: дилемма заключенного
• Докинз: приятные парни финишируют первыми
• Аксельрод Повторяющаяся дилемма заключенного Python библиотека
• Играйте в повторяющуюся дилемму заключенного на gametheorygames.nl
• Играть в Prisoner's Dilemma на oTree (Н / Д 11-5-17)
• Ники Кейса Эволюция доверия, пример игры-пожертвования
• Многократная онлайн-игра "Дилемма заключенного" Уэйн Дэвис