Фундаментальный многоугольник - Fundamental polygon
В математика, а фундаментальный многоугольник можно определить для каждого компактная риманова поверхность рода больше 0. Он кодирует не только топологию поверхности через ее фундаментальная группа но также определяет риманову поверхность с точностью до конформной эквивалентности. Посредством теорема униформизации, каждая компактная риманова поверхность имеет односвязную универсальную накрывающую поверхность, заданную ровно одним из следующих утверждений:
- то Сфера Римана,
- то комплексная плоскость,
- единичный диск D эквивалентно верхняя полуплоскость ЧАС.
В первом случае нулевого рода поверхность конформно эквивалентна сфере Римана.
Во втором случае рода один поверхность конформно эквивалентна тору C/ Λ для некоторой решетки Λ в C. Фундаментальный многоугольник Λ, если он предполагается выпуклым, может быть взят либо за параллелограмм периодов, либо за центрально-симметричный шестиугольник, что впервые было доказано Федоров в 1891 г.
В последнем случае рода грамм > 1 риманова поверхность конформно эквивалентна ЧАС/ Γ, где Γ - Фуксова группа из Преобразования Мебиуса. Фундаментальной областью для Γ является выпуклый многоугольник гиперболической метрики на ЧАС. Они могут быть определены многоугольниками Дирихле и иметь четное число сторон. Строение фундаментальной группы Γ можно прочитать с такого многоугольника. Используя теорию квазиконформные отображения и Уравнение Бельтрами, можно показать, что существует канонический выпуклый многоугольник Дирихле с 4грамм стороны, сначала определенные Фрике, что соответствует стандартному представлению Γ как группы с 2грамм генераторы а1, б1, а2, б2, ..., аграмм, бграмм и единственное отношение [а1,б1][а2,б2] ⋅⋅⋅ [аграмм,бграмм] = 1, где [а,б] = а б а−1б−1.
Любая риманова метрика на ориентированном замкнутом двумерном многообразии M определяет сложную структуру на M, изготовление M компактная риманова поверхность. Используя фундаментальные многоугольники, следует, что два ориентированных замкнутых 2-многообразия классифицируются по их роду, который составляет половину ранга абелевой группы Γ / [Γ, Γ], где Γ = π1(M). Более того, из теории квазиконформных отображений также следует, что две компактные римановы поверхности диффеоморфны тогда и только тогда, когда они гомеоморфны. Следовательно, два замкнутых ориентированных 2-многообразия гомеоморфны тогда и только тогда, когда они диффеоморфны. Такой результат также можно доказать с помощью методов дифференциальная топология.[1][2]
Фундаментальные полигоны первого рода


Параллелограммы и центрально-симметричные шестиугольники
В случае рода один фундаментальный выпуклый многоугольник для действия ищется сдвигом Λ = Z а ⊕ Z б на р2 = C куда а и б линейно независимы над р. (После выполнения реального линейного преобразования на р2, при необходимости можно считать, что Λ = Z2 = Z + Z я; для римановой поверхности рода один она может иметь вид Λ = Z2 = Z + Z ω, причем Im ω> 0.) A фундаментальная область задается параллелограммом s Икс + т у за 0 < s , т < 1 куда Икс и у образующие Λ.
Если C является внутренностью фундаментального выпуклого многоугольника, то переводы C + Икс крышка р2 в качестве Икс пробегает Λ. Отсюда следует, что граничные точки C состоят из перекрестков C ∩ (C + Икс). Это компактные выпуклые множества в ∂C а значит, либо вершины C или стороны C. Отсюда следует, что каждая закрытая сторона C можно записать так. Переводчик -Икс следует, что C ∩ (C − Икс) также является стороной C. Таким образом стороны C встречаются параллельно парами одинаковой длины. Конечные точки двух таких параллельных сегментов равной длины могут быть соединены таким образом, чтобы они пересекались, и пересечение происходило в средних точках отрезков прямой, соединяющих конечные точки. Отсюда следует, что пересечение всех таких отрезков происходит в одной точке. Если перевести эту точку в начало координат, то получится, что многоугольник центрально симметричен; то есть, если точка z находится в многоугольнике, так же как -z.
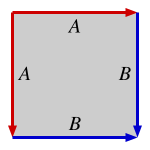
Легко увидеть переводы центрально-симметричного выпуклого шестиугольника на мозаику плоскости. Если А является точкой шестиугольника, то решетка порождается векторами смещения AB и AC куда B и C две вершины, которые не являются соседями А а не наоборот А. Действительно, на втором рисунке показано, как шестиугольник эквивалентен параллелограмму, полученному перемещением двух треугольников, отрубленных отрезками. AB и AC. Также хорошо на первом рисунке показан другой способ сопоставления мозаики параллелограммами с шестиугольной мозаикой. Если центр шестиугольника равен 0, а вершины по порядку равны а, б, c, −а, −б и -c, то Λ - абелева группа с образующими а + б и б + c.
Примеры фундаментальных многоугольников, порожденных параллелограммами
Существует ровно четыре топологии, которые можно создать, определяя стороны параллелограмма разными способами (ниже изображены квадратами):
 Сфера[3] |  Реальная проективная плоскость |  Бутылка Клейна | 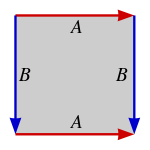 Тор |
- Сфера: или же
- Реальная проективная плоскость: или же
- Бутылка Клейна: или же
- Тор: или же
Теорема Федорова
Теорема Федорова, установленный российским кристаллографом Евграф Федоров в 1891 году утверждает, что параллелограммы и центрально-симметричные шестиугольники - единственные выпуклые многоугольники, которые являются фундаментальными областями.[4] Есть несколько доказательств этого, некоторые из последних связаны с результатами в теория выпуклости, то геометрия чисел и упаковка круга, такой как Неравенство Брунна – Минковского..[5]Два элементарных доказательства благодаря Х. С. М. Коксетер и Вороной будут представлены здесь.[6][7]
Доказательство Кокстера основывается на предположении, что существует центрально-симметричный выпуклый многоугольник C с 2м стороны. Тогда большой замкнутый параллелограмм образовался из N2 фундаментальные параллелограммы выложены переводами C которые выходят за края большого параллелограмма. Это индуцирует замощение на торе C/NΛ. Позволять v, е и ж - количество вершин, ребер и граней в этом мозаике (с учетом отождествлений в фактор-пространстве). Тогда, поскольку Характеристика Эйлера – Пуанкаре тора равен нулю,
С другой стороны, поскольку каждая вершина находится как минимум на 3 разных ребрах и каждое ребро находится между двумя вершинами,
Более того, поскольку каждое ребро находится ровно на двух гранях,
Следовательно
так что
как требуется.
Доказательство Вороного начинается с наблюдения, что каждое ребро C соответствует элементу Икс из Λ. Фактически ребро является ортогональной биссектрисой радиуса от 0 до Икс. Следовательно, основание перпендикуляра от 0 к каждому ребру лежит внутри каждого ребра. Если у любая точка решетки, то 1/2 у не может лежать в C; если да, то –1/2 у также будет лежать в C, противоречащие C фундаментальная область для Λ. Пусть ±Икс1, ..., ±Иксм быть 2м различные точки Λ, соответствующие сторонам C. Исправить генераторы а и б из Λ. Таким образом Икся = αя а + βя б, где αя и βя целые числа. Это невозможно для обоих αя и βя быть четным, поскольку в противном случае ± 1/2 Икся будет точкой Λ на стороне, что противоречит C являясь фундаментальной областью. Итак, есть три возможности для пары целых чисел (αя, βя) по модулю 2: (0,1), (1,0) и (1,1). Следовательно, если м > 3, было бы Икся и Иксj с я ≠ j с обеими координатами Икся − Иксj четное, т.е. 1/2 (Икся + Иксj) лежит в Λ. Но это середина отрезка, соединяющего две внутренние точки ребер, и, следовательно, лежит в C, внутренность многоугольника. Это снова противоречит тому, что C является фундаментальной областью. Так сокращение до абсурда м ≤ 3, как заявлено.
Области Дирихле – Вороного.
Для решетки Λ в C = р2фундаментальная область может быть определена канонически, используя конформную структуру C. Отметим, что группа конформных преобразований C задается сложными аффинными преобразованиями грамм(z) = az + б с а ≠ 0. Эти преобразования сохраняют евклидову метрику d(z, ш) = |z − ш| с точностью до фактора, а также с сохранением ориентации. Это подгруппа группы Мёбиуса, фиксирующая точку в ∞. Метрическая структура может использоваться для определения канонической фундаментальной области с помощью C = {z: d(z, 0) < d(z, λ) для всех λ ≠ 0 в Λ}. (Из определения очевидно, что это фундаментальная область.) Это пример Домен Дирихле или же Диаграмма Вороного: поскольку комплексные сдвиги образуют абелеву группу, поэтому коммутируют с действием Λ, эти понятия совпадают. Каноническая фундаментальная область для Λ = Z + Zω с Я ω > 0 является либо симметричным выпуклым параллелограммом, либо шестиугольником с центром 0. В силу конформной эквивалентности период ω можно дополнительно ограничить, чтобы удовлетворить |Re ω| ≤ 1/2 и |ω| ≥ 1. В качестве Дирихле показал («Теорема Дирихле о шестиугольнике», 1850 г.), почти для всех ω фундаментальная область - шестиугольник. За Re ω > 0, середины сторон равны ± 1/2, ±ω/ 2 и ±(ω – 1)/2; стороны делят пополам соответствующие радиусы из 0 ортогонально, что полностью определяет вершины. Фактически первая вершина должна иметь вид (1 + ix)/2 и ω(1 + иу)/2 с Икс и у настоящий; так что если ω = а + ib, тогда а – к = 1 и Икс = б + ай. Следовательно у = (а – 1)/б и Икс = (а2 + б2 – а)/б. Таким образом, шесть вершин ±ω(1 – иу)/2 и ±(1 ± ix)/2.[8]
Фундаментальные многоугольники в высшем роде
Обзор
Каждая компактная риманова поверхность Икс имеет универсальная покрывающая поверхность которая является односвязной римановой поверхностью Икс. В фундаментальная группа из Икс выступает в качестве преобразования колоды из Икс и может быть отождествлена с подгруппой Γ группы биголоморфизмы из Икс. Таким образом, группа Γ свободно действует на Икс с компактным факторпространством Икс/ Γ, которую можно отождествить с Икс. Таким образом, классификация компактных римановых поверхностей сводится к изучению возможных групп Γ. Посредством теорема униформизации Икс является либо сферой Римана, либо комплексной плоскостью, либо единичным кругом / верхней полуплоскостью. Первым важным инвариантом компактной римановой поверхности является ее род, топологический инвариант, задаваемый половиной ранга абелевой группы Γ / [Γ, Γ] (который можно отождествить с группа гомологии ЧАС1(Икс, Z)). Род равен нулю, если накрывающим является сфера Римана; один, если это комплексная плоскость; и больше единицы, если это единичный диск или верхняя полуплоскость.[9]
Бигомоломорфизмы сферы Римана - это просто комплексные преобразования Мёбиуса, и каждое неединичное преобразование имеет по крайней мере одну неподвижную точку, поскольку соответствующая комплексная матрица всегда имеет по крайней мере один ненулевой собственный вектор. Таким образом, если Икс - сфера Римана, то Икс должен быть односвязным и биголоморфным сфере Римана, нулевой род Риманова поверхность. Когда Икс - комплексная плоскость, группа биголоморфизмов - это аффинная группа, комплексные преобразования Мёбиуса фиксируют ∞, поэтому преобразования грамм(z) = az + б с а ≠ 0. Нетождественные преобразования без неподвижных точек - это просто преобразования с а = 1 и б ≠ 0, т.е. ненулевые переводы. Таким образом, группу Γ можно отождествить с решеткой Λ в C и Икс с частным C/ Λ, как описано в разделе о фундаментальных многоугольниках рода один. В третьем случае, когда Икс - единичный круг или верхняя полуплоскость, группа биголоморфизмов состоит из комплексных преобразований Мёбиуса, фиксирующих единичную окружность или действительную ось. В первом случае преобразования соответствуют элементам группы SU (1, 1) / {±я}; в последнем случае они соответствуют действительным преобразованиям Мёбиуса, поэтому элементы SL (2, р)/{±я}.[9]
Изучение и классификация возможных групп Γ, которые свободно действуют на единичном круге или верхней полуплоскости с компактным фактором - Фуксовы группы первого типа - могут быть выполнены путем изучения их фундаментальных многоугольников, как описано ниже. В качестве Пуанкаре Как можно заметить, каждый такой многоугольник обладает особыми свойствами, а именно выпуклостью и естественным спариванием сторон. Они не только позволяют восстановить группу, но и обеспечивают явное представление группы с помощью генераторов и отношений. Наоборот, Пуанкаре доказал, что любой такой многоугольник порождает компактную риманову поверхность; фактически, теорема Пуанкаре о многоугольниках применялась к многоугольникам более общего вида, где многоугольник мог иметь идеальные вершины, но его доказательство было полным только в компактном случае, без таких вершин. Без предположений о выпуклости многоугольника полные доказательства были даны Маскит и де Рам, основанный на идее Сигель, и его можно найти в Бирдон (1983), Иверсен (1992) и Стиллвелл (1992). Каратеодори дал элементарную трактовку существования мозаика треугольниками Шварца, т.е. замощения геодезическими треугольниками с углами π/а, π/б, π/c с суммой меньше чем π куда а, б, c целые числа. Когда все углы равны π/2грамм, это устанавливает тайлинг регулярными 4 г-сторонние гиперболические многоугольники и, следовательно, существование конкретной компактной римановой поверхности рода грамм как факторное пространство. Этот частный пример, в котором есть циклическая группа Z2грамм бигомоломорфных симметрий, используется в дальнейшем развитии.[9]
Из классификации с точностью до гомеоморфизма и диффеоморфизма компактных римановых поверхностей следует классификация замкнутых ориентируемых 2-многообразий с точностью до гомеоморфизма и диффеоморфизма: любые два 2-многообразия одного рода диффеоморфны. Фактически, используя разбиение единицы, каждое замкнутое ориентируемое двумерное многообразие допускает Риманова метрика. Для компактной римановой поверхности также может быть введена конформная метрика, которая является конформной, так что в голоморфных координатах метрика принимает вид ρ(z) |дз|2. После выбора этой метрики локально биголоморфные отображения являются в точности сохраняющими ориентацию диффеоморфизмами, которые являются конформными, т.е. масштабируют метрику гладкой функцией. Существование изотермические координаты - что можно доказать, используя либо локальные теоремы существования лапласиана или Уравнение Бельтрами - показывает, что каждому замкнутому ориентированному двумерному риманову многообразию может быть дана комплексная структура, совместимая с его метрикой, и, следовательно, оно имеет структуру компактной римановой поверхности. Эта конструкция показывает, что классификация замкнутых ориентируемых 2-многообразий с точностью до диффеоморфизма или гомеоморфизма сводится к случаю компактных римановых поверхностей.[10]
Классификация с точностью до гомеоморфизма и диффеоморфизма компактных римановых поверхностей может быть выполнена с использованием фундаментального многоугольника. Действительно, как заметил Пуанкаре выпуклые фундаментальные многоугольники для компактных римановых поверхностей ЧАС/ Γ можно построить, адаптируя метод Дирихле из евклидова пространства к гиперболическому пространству. Затем, следуя Неванлинне и Йосту, фундаментальную область можно поэтапно модифицировать, чтобы получить невыпуклый многоугольник с вершинами, лежащими в одной орбите Γ, и кусочно-геодезическими сторонами. Отношение спаривания на сторонах также изменяется на каждом из этих шагов. Каждый шаг включает разрезание многоугольника диагональным геодезическим сегментом внутри многоугольника и повторную сборку многоугольника с помощью одного из преобразований Мёбиуса, участвующих в формировании пары. Никакие две парные стороны не могут иметь общую вершину в конечном соотношении спаривания, которое удовлетворяет свойствам, аналогичным свойствам исходного отношения. Этот многоугольник, в свою очередь, может быть последовательно модифицирован путем повторной сборки многоугольника после разрезания его на диагональный кусочно-геодезический сегмент внутри. Последний многоугольник имеет 4грамм эквивалентные вершины, стороны которых кусочно-геодезические. Стороны помечены элементами группы, которые задают преобразование Мёбиуса для парной стороны. Чтобы маркировка была
так что Γ порождается ая и бя при единственном отношении

Род нулевой поверхности (сфера)

Род один поверхность (тор)

Поверхность рода два

Род три поверхности
Используя теорию номера перекрестков, из этого следует, что форма, полученная соединением вершин геодезическими, также является собственным многоугольником, не обязательно выпуклым, а также фундаментальной областью с теми же элементами группы, которые образуют пары. Это дает фундаментальный многоугольник с ребрами, заданными геодезическими сегментами, и со стандартной разметкой. Абелианизация Γ, фактор-группа Γ / [Γ, Γ], - свободная абелева группа с 2грамм генераторы. Таким образом род грамм является топологическим инвариантом. Легко видеть, что две римановы поверхности одного рода гомеоморфны, поскольку как топологическое пространство, поскольку они получаются отождествлением сторон 4грамм-сторонний многоугольник - евклидов многоугольник в Модель Кляйна - диффеоморфизмами между парными сторонами.[11] Применяя эту конструкцию к регулярным 4грамм-сторонний многоугольник позволяет рассматривать риманову поверхность топологически как бублик с грамм дыры, стандартное описание ориентированных поверхностей во вводных текстах по топологии.[12][13]
Есть еще несколько результатов:
- Две гомеоморфные римановы поверхности диффеоморфны.
- Любой выпуклый фундаментальный многоугольник рода грамм имеет N вершины, где 4грамм ≤ N ≤ 12грамм – 6.
- Многоугольник Дирихле в роде грамм точно 12грамм – 6 вершины для плотного открытого множества центров.
- Каждый род грамм Риманова поверхность имеет фундаментальный многоугольник Фрике, т.е. выпуклый многоугольник с каноническим спариванием между сторонами. (Многоугольник не обязательно должен быть многоугольником Дирихле.)
- После подходящей нормализации и разметки генераторов фундаментальной группы многоугольник Фрике определяется однозначно и 6грамм – 6 описывающие его реальные параметры могут использоваться как глобальные реальные аналитические параметры для Пространство Тейхмюллера в роду грамм.
Эти результаты связаны с взаимосвязью между гомеоморфизмами и фундаментальной группой: это отражает тот факт, что группа классов отображения римановой поверхности - группа квазиконформных самогомоморфизмов римановой поверхности ЧАС/ Γ по модулю гомотопных единице - можно отождествить с группа внешних автоморфизмов группы Γ ( Теорема Дена – Нильсена – Бэра. ).[14] Чтобы увидеть эту связь, обратите внимание, что если ж является квазиконформным гомеоморфизмом Икс1 = ЧАС/ Γ1 на Икс2 = ЧАС/ Γ2, тогда ж поднимается до квазиконформного гомеоморфизма ж из ЧАС на себя. Этот лифт единственен с точностью до предварительной композиции с элементами из Γ1 и пост-композиция с элементами Γ2. Если πя это проекция ЧАС на Икся, тогда ж ∘ π1 = π2 ∘ ж и Γя это просто группа гомеоморфизмов грамм из ЧАС такой, что πя ∘ грамм = πя. Если следует, что ж грамм = θ(грамм) ж за грамм в Γ1 куда θ является групповым изоморфизмом Γ1 на Γ2. Другой выбор ж изменения θ композицией с внутренним автоморфизмом: такие изоморфизмы называются эквивалент.[15]
Два изоморфизма θ и θ′ Эквивалентны тогда и только тогда, когда соответствующие гомеоморфизмы ж и ж' гомотопны. На самом деле достаточно показать, что квазиконформный самогомеоморфизм ж поверхности индуцирует внутренний автоморфизм фундаментальной группы тогда и только тогда, когда она гомотопна тождественному отображению: другими словами, гомоморфизм квазиконформной группы самогомеоморфизмов группы ЧАС/ Γ в Out Γ переходит в группу классов отображений, на которой он инъективен. Действительно, предположим сначала, что F(т) - непрерывный путь самогомеоморфизмов с F(0) = id и F(1) = ж. Тогда существует непрерывный подъем F(т) с F(0) = идентификатор. Причем для каждого грамм в Γ, F(т) ∘ грамм ∘ F(т)−1 является непрерывно меняющимся элементом Γ, равным грамм за т = 0; поэтому дискретность Γ заставляет этот элемент быть постоянным и, следовательно, равным грамм так что F(т) коммутирует с Γ, поэтому F(1) индуцирует тривиальный автоморфизм. Если с другой стороны F является квазиконформным подъемом ж индуцируя внутренний автоморфизм Γ, после композиции с элементом Γ, если необходимо, можно считать, что F коммутирует с Γ. С F квазиконформно, оно продолжается до квазисимметричного гомеоморфизма окружности, который также коммутирует с Γ. Каждый грамм ≠ id в Γ гиперболичен, поэтому имеет две неподвижные точки на окружности а± так что для всех остальных точек z, грамм±п(z) как правило а± в качестве п стремится к бесконечности. Следовательно F необходимо исправить эти точки; так как эти точки плотны в круге при грамм меняется, отсюда следует, что F фиксирует единичный круг. Позволять μ = Fz / Fz, так что μ является Γ-инвариантным дифференциалом Бельтрами. Позволять F(т) - решение уравнения Бельтрами tμ нормализованный, чтобы зафиксировать три точки на единичной окружности. потом F(т) коммутирует с Γ, а значит, как и для F = F(1), является единицей на единичной окружности. По конструкции F(т) является изотопией между единицей и F. Это доказывает приемистость.[15]
Доказательство сюръективности основано на сравнении гиперболической метрики на D с метрикой длины слова на Γ.[16] Полагая без ограничения общности, что 0 лежит внутри выпуклого фундаментального многоугольника C и грамм является элементом Γ, луч от 0 до грамм(0) - гиперболическая геодезическая - проходит через последовательность переводов C. Каждый из них получается из предыдущего путем применения генератора Γ или фиксированного произведения образующих (если последовательные переводы пересекаются в вершине). Отсюда следует, что гиперболическое расстояние между 0 и грамм(0) меньше 4грамм умноженное на длину слова грамм плюс удвоенный диаметр основного многоугольника. Таким образом, метрика на Γ d1(грамм, час) = L(час−1грамм) определяется длиной слова L(грамм) удовлетворяет
для положительных констант а и б. Наоборот, есть положительные постоянные c и d такой, что
Полигоны Дирихле
Учитывая точку в верхняя полуплоскость ЧАС, а дискретный подгруппа Γ из PSL (2, р) что действует свободно прерывисто на верхней полуплоскости, то можно определить Многоугольник Дирихле как набор точек
Здесь, d гиперболический метрика в верхней полуплоскости. Метрический фундаментальный многоугольник чаще называют Многоугольник Дирихле.
- Этот фундаментальный многоугольник является фундаментальная область.
- Этот фундаментальный многоугольник выпуклый в этом геодезический соединение любых двух точек многоугольника полностью содержится внутри многоугольника.
- В диаметр из F меньше или равен диаметру ЧАС/ Γ.В частности, закрытие F компактный.
- Если Γ не имеет неподвижных точек в ЧАС и ЧАС/ Γ компактно, то F будет иметь конечное число сторон.
- Каждая сторона многоугольника представляет собой геодезический дуга.
- Для каждой стороны s многоугольника есть ровно одна другая сторона s′ Такой, что GS = s′ для некоторых грамм в Γ. Таким образом, у этого многоугольника будет четное количество сторон.
- Набор элементов группы грамм которые соединяют стороны друг с другом генераторы Γ, и нет меньшего множества, которое порождает Γ.
- Верхняя полуплоскость облицована закрытием F под действием Γ. То есть, куда закрытие F.
Нормализованный многоугольник
В этом разделе, начиная с произвольного многоугольника Дирихле, будет дано описание метода Неванлинна (1955), разработанная в Йост (2002), для преобразования многоугольника в невыпуклый многоугольник с 4грамм эквивалентные вершины и каноническое спаривание по сторонам. Эта трактовка является аналитическим аналогом классической топологической классификации ориентируемых двумерных многогранников, представленной в Зейферт и Трелфолл (1934).
Канонический многоугольник Фрике
Для римановой поверхности рода грамм больше единицы, Фрике описал еще один фундаментальный многоугольник, Канонический многоугольник Фрике, который является очень частным примером многоугольника Дирихле. Многоугольник связан со стандартным представлением основной группы поверхности. Оригинальная конструкция Фрике сложна и описана в Фрике и Кляйн (1897). Используя теорию квазиконформные отображения из Альфорс и Берс, Кин (1965) дал новую, более короткую и точную версию конструкции Фрике. Канонический многоугольник Фрике обладает следующими свойствами:
- Вершин многоугольника Фрике 4грамм вершины, лежащие на орбите Γ. К вершина означает точку, где встречаются две стороны.
- Стороны сопоставляются в различных парах, так что существует единственный элемент Γ, переносящий сторону к парной стороне, меняя ориентацию на обратную. Поскольку действие группы Γ сохраняет ориентацию, если одна сторона называется , то другой из пары может быть помечен противоположной ориентацией .
- Ребра стандартного многоугольника можно расположить так, чтобы список смежных сторон имел вид . То есть пары сторон могут быть расположены таким образом, чтобы они чередовались.
- Стороны представляют собой геодезические дуги.
- Каждый из внутренних углов многоугольника Фрике строго меньше π, так что многоугольник является строго выпуклым, а сумма этих внутренних углов равна 2π.
Приведенной выше конструкции достаточно, чтобы гарантировать, что каждая сторона многоугольника представляет собой замкнутую (нетривиальную) петлю на римановой поверхности ЧАС/ Γ. Таким образом, каждая сторона может быть элементом фундаментальная группа . В частности, фундаментальная группа имеет 2грамм генераторы , с ровно одним определяющим ограничением,
- .
Род римановой поверхности ЧАС/ Γ является грамм.
Площадь
Площадь стандартного фундаментального многоугольника равна куда грамм - род римановой поверхности (эквивалентно, где 4грамм - количество сторон многоугольника). Поскольку стандартный многоугольник является представителем ЧАС/ Γ общая площадь римановой поверхности равна площади стандартного многоугольника. Формула площади следует из Теорема Гаусса – Бонне и в некотором смысле обобщается через Формула Римана – Гурвица.
Явная форма для стандартных многоугольников
Явные выражения могут быть даны для обычного стандарта 4грамм-сторонний многоугольник с вращательной симметрией. В данном случае это род Риманова поверхность с грамм-кратная вращательная симметрия, группа может быть задана формулой генераторы . Эти генераторы задаются следующими дробно-линейные преобразования действуя на верхняя полуплоскость:
за . Параметры представлены как
и
и
Можно проверить, что эти генераторы подчиняются ограничению
что дает совокупность групповая презентация.
Смотрите также
Примечания
- ^ Видеть:
- ^ Видеть:
- ^ Пример построение сферы из фундаментального многоугольника.
- ^ Е. Федоров (1891) «Симметрія на плоскости» (Симметрия на площади, Симметрия на плоскости), Записки Императорского С.-Петербургского минералогического общества (Записки Императорскова Санкт-Петербургскова Минералогического общества, Известия Императорского Санкт-Петербургского минералогического общества), 2-я серия, 28 : 345–390.
- ^ Видеть:
- ^ Доказательство Вороного имеет то преимущество, что оно обобщается на п размерности: он показывает, что если переводить центрально-симметричный выпуклый многогранник тессалатный рп, то многогранник имеет не более 2 (2п - 1) лица.
- ^ Видеть:
- ^ Видеть:
- Кассель 1994
- Колмогоров, Юкшкевич 2001, стр. 157–159
- ^ а б c Бирдон 1984
- ^ Имаёши и Танагути 1992
- ^ Обратите внимание, что простой многоугольник на плоскости с п ≥ 4 вершин гомеоморфно одной, а значит, любой выпуклой п-угольник кусочно линейным гомеоморфизмом, линейным на ребрах: это следует индукцией по п из наблюдения Макс Ден что любой простой многоугольник имеет диагональ, т.е. внутреннюю хорду между вершинами, поэтому может быть разбит на более мелкие многоугольники; видеть Гуггенхаймер (1977). Для обычных 4грамм-угольник, соединение сторон можно сделать линейным путем изменения параметров треугольников, составленных из центра и одной стороны каждой пары сторон.
- ^ Йост 2002, стр. 47–57
- ^ Шастри 2010
- ^ Фарб и Маргалит 2012
- ^ а б Альфорс 2006, стр. 67–68
- ^ Фарб и Маргалит 2012, стр. 230–236
Рекомендации
- Альфорс, Ларс В. (2006), Лекции о квазиконформных отображениях, Серия университетских лекций, 38 (Второе изд.), Американское математическое общество, ISBN 978-0-8218-3644-6
- Appell, P .; Goursat, E .; Фату, П. (1930), Теория функций переменных единой переменной, Том II, Автоморфы функций, Gauthier-Vi] lars, стр. 102–154.
- Bambah, R.P .; Давенпорт, Х. (1952), "Покрытие n-мерного пространства сферами", J. London Math. Soc., 27 (2): 224–229, Дои:10.1112 / jlms / s1-27.2.224
- Бирдон, Алан Ф. (1983), Геометрия дискретных групп, Springer-Verlag, ISBN 978-0-387-90788-8
- Бирдон, Алан Ф. (1984), Грунтовка для римановых поверхностей, Серия лекций Лондонского математического общества, 78, Издательство Кембриджского университета, ISBN 978-0-521-27104-2
- Бонк, Мариус; Шрамм, Одед (2000), "Вложения гиперболических пространств Громова", Геом. Funct. Анальный., 10 (2): 266–306, CiteSeerX 10.1.1.47.7874, Дои:10.1007 / с000390050009
- Бёрёчки, Кароли-младший (2004), Готовая упаковка и укрытие, Кембриджские трактаты по математике, 154, Издательство Кембриджского университета, ISBN 978-0-521-80157-7
- Бурдон, Марк; Пажо, Эрве (2002), «Квазиконформная геометрия и гиперболическая геометрия», у Марка Бургера; Алессандра Иоцци (ред.), Жесткость в динамике и геометрии, Springer, стр. 1–17, ISBN 978-3-540-43243-2
- Баззар, Питер (1992), Геометрия и спектры компактных римановых поверхностей, Успехи в математике, 106, Биркхойзер, ISBN 978-0-8176-3406-3
- Касселс, Дж. У. С. (1997), «IX. Упаковки», Введение в геометрию чисел, Классика математики, Springer-Verlag, ISBN 978-3-540-61788-4
- Кокстер, Х. С. М (1962), "Классификация зоноэдров с помощью проективных диаграмм", J. Math. Pures Appl., 41: 137–156
- Кокстер, Х. С. М.; Мозер, В. О. Дж. (1980), Генераторы и соотношения для дискретных групп, 14 (Четвертое издание. Ergebnisse der Mathematik und ihrer Grenzgebiete ed.), Springer-Verlag, ISBN 978-3-540-09212-4
- Эгглстон, Х. Г. (1958), Выпуклость, Кембриджские трактаты по математике и математической физике, Издательство Кембриджского университета
- Фарб, Бенсон; Маргалит, Дан (2012), Праймер по отображению групп классов, Принстонская математическая серия, 49, Princeton University Press, ISBN 978-0-691-14794-9
- Farkas, Hershel M .; Кра, Ирвин (1980), Римановы поверхности, Springer-Verlag, ISBN 978-0-387-90465-8
- Фенчель, Вернер; Нильсен, Якоб (2003), Разрывные группы изометрий в гиперболической плоскости, Исследования де Грюйтера по математике, 29, Вальтер де Грюйтер, ISBN 978-3-11-017526-4
- Фрике, Роберт; Кляйн, Феликс (1897), Vorlesungen über die Theorie der automorphen Funktionen, Band 1: Die gruppentheoretischen Grundlagen, Teubner, стр. 236–237, 295–320
- Грюнбаум, Бранко; Шепард, Г.С. (1987), Плитки и узоры, У. Х. Фриман, ISBN 978-0-7167-1193-3
- Гуггенхаймер, Х. (1977), «Теорема Жордана и неопубликованная рукопись Макса Дена» (PDF), Архив истории точных наук, 17 (2): 193–200, CiteSeerX 10.1.1.374.1893, Дои:10.1007 / BF02464980, JSTOR 41133486, МИСТЕР 0532231
- Хирш, Моррис В. (1994), Дифференциальная топология, Тексты для выпускников по математике, 33, Springer-Verlag, ISBN 978-0-387-90148-0
- Imayoshi, Y .; Танигучи, М. (1992), Введение в пространства Тейхмюллера, Springer-Verlag, ISBN 978-0-387-70088-5
- Иверсен, Биргер (1992), Гиперболическая геометрия, Студенческие тексты Лондонского математического общества, 25, Издательство Кембриджского университета, ISBN 978-0-521-43508-6
- Йост, Юрген (2002), Компактные римановы поверхности (2-е изд.), Springer-Verlag, ISBN 978-3-540-43299-9
- Капович Илья; Бенакли, Надя (2002), "Границы гиперболических групп", Комбинаторная и геометрическая теория групп, Contemp. Математика, 296, Американское математическое общество, стр. 39–93
- Кин, Линда (1965), «Канонические многоугольники для конечно порожденных фуксовых групп», Acta Math., 115: 1–16, Дои:10.1007 / bf02392200
- Кин, Линда (1966), "Внутренние модули на римановых поверхностях", Анна. математики., 84 (3): 404–420, Дои:10.2307/1970454, JSTOR 1970454
- Колмогоров, А. Н .; Юкшкевич А.П., ред. (2001), Математика XIX века: математическая логика, алгебра, теория чисел, теория вероятностей, Спрингер, ISBN 978-3764364410
- Лехто, Олли (1987), Однолистные функции и пространства Тейхмюллера, Тексты для выпускников по математике, 109, Springer-Verlag, ISBN 978-0-387-96310-5
- Люстерник, Л.А. (1966), Выпуклые фигуры и многогранники, переведенный Дональдом Л. Барнеттом, Бостон: D. C. Heath and Co.
- Неванлинна, Рольф (1953), Uniformisierung, Die Grundlehren der Mathematischen Wissenschaften в Einzeldarstellungen mit besonderer Berücksichtigung der Anwendungsgebiete (на немецком языке), 64, Springer-Verlag
- Зейферт, Герберт; Трелфолл, Уильям (1934), Учебник топологии, Чистая и прикладная математика, 89, перевод Майкла А. Гольдмана, Academic Press, ISBN 978-0-12-634850-7
- Шастри, Анант Р. (2011), Элементы дифференциальной топологии, CRC Press, ISBN 978-1-4398-3160-1
- Сигель, К. Л. (1971), Вопросы теории сложных функций, Vol. II. Автоморфные функции и абелевы интегралы, перевод А. Шеницера; М. Третьков, Wiley-Interscience
- Стиллвелл, Джон (1992), Геометрия поверхностей, Universitext, Springer-Verlag, ISBN 978-0-387-97743-0
- Цзун, Чуанмин (2014), «Упаковка, покрытие и мозаика в двумерных пространствах», Expositiones Mathematicae, 32 (4): 297–364, Дои:10.1016 / j.exmath.2013.12.002










































