Парадокс колеса Аристотеля - Aristotles wheel paradox

Парадокс колеса Аристотеля это парадокс или проблема появляется в Греческий работай Mechanica традиционно приписывается Аристотель.^[1] Колесо можно изобразить в двух измерениях с помощью двух круги. Большой круг касается горизонтальной поверхности (например, дороги), по которой он может катиться. Меньший круг имеет такой же центр и жестко прикреплен к большему. Меньший круг может изображать борт шины, обод, на котором установлена шина, ось и т. Д. Предположим, что больший круг катится без проскальзывания (или заноса) на полный оборот. Расстояния, перемещаемые обоими кругами, имеют одинаковую длину, что показано синей и красной пунктирными линиями и расстоянием между двумя черными вертикальными линиями. Расстояние для большего круга равно его длина окружности, но расстояние для меньшего круга больше, чем его окружность: парадокс или проблема.

Парадокс не ограничивается колесом. Другие объекты, изображенные в двух измерениях, демонстрируют такое же поведение. Рулон ленты делает. Типичная круглая бутылка или перевернутая на бок банка баночка - нет; меньший кружок, изображающий горлышко или горлышко бутылки или фляги.

Есть несколько вещей, которые будут изображены коричневой горизонтальной линией на изображении, касающейся меньшего круга, а не большего. Примерами являются типичное колесо поезда с фланцем или штанга, сидящая на скамье. Драбкин назвал эти дела II и те, что изображены на изображении, делом I.^[1] Применяется аналогичный, но не идентичный анализ.

История парадокса

В древности

В древности проблема колеса описывалась в аристотелевской Mechanica, а также в Mechanica из Герой Александрии.^[1] В первом случае оно отображается как «Проблема 24», где описание колеса дано следующим образом.

Ибо пусть будет больший круг ΔZΓ, меньший EHB, и А в центре обоих; пусть ZI будет линией, которая разворачивается самой большой, а HK - линией, которую меньшая разворачивает сама по себе, равной ZΛ. Когда я перемещаю меньший круг, я перемещаю тот же центр, то есть A; пусть к нему прикрепится больший. Когда AB становится перпендикулярным HK, в то же время AΓ становится перпендикулярным ZΛ, так что он всегда будет проходить равное расстояние, а именно HK для окружности HB и ZΛ для ZΓ. Если четверть развернется на равное расстояние, ясно, что весь круг развернется на такое же расстояние, что и весь круг, так что, когда прямая BH подходит к K, окружность ZΓ будет ZΛ, и весь круг будет развернут. Таким же образом, когда я перемещаю большой круг, подгоняя к нему малый, причем их центр будет таким же, AB будет перпендикулярно и под прямым углом одновременно с AΓ, последний к ZI, первый к HΘ. Таким образом, когда один завершит линию, равную HΘ, а другой - ZI, и ZA снова станет перпендикулярно ZΛ, а HA - HK, так что они будут такими же, как в начале в Θ и I.^[2]

Затем проблема формулируется:

Теперь, поскольку нет остановки большего для меньшего, так что оно [большее] остается в течение некоторого промежутка времени в одной и той же точке, и поскольку меньший не перепрыгивает через какую-либо точку, странно, что большее проходит путь равен пути меньшего, и опять же, меньший проходит путь, равный пути большего. Более того, примечательно, что, хотя в каждом случае есть только одно движение, центр, который перемещается в одном случае, катится на большое расстояние, а в другом - на меньшее.^[1]

В научной революции

Математик Джероламо Кардано обсуждает проблему колеса в его 1570 Opus novum de ratioibus numerorum,^[3] не согласен с презумпцией анализа проблемы с точки зрения движения.^[1] Мерсенн далее обсуждал колесо в его 1623 Quaestiones Celeberrimae в Genesim,^[4] где он предполагает, что проблема может быть проанализирована путем расширения и сжатия двух кругов. Но Мерсенн остался недоволен его пониманием, написанием,

На самом деле мне никогда не удавалось обнаружить, и я не думаю, что кому-либо еще удавалось обнаружить, касается ли меньший круг одной и той же точки дважды или движется прыжками и скольжением.^[1]

В его Две новые науки, Галилео использует проблему колеса, чтобы привести доводы в пользу определенного рода атомизм. Галилей начинает свой анализ с рассмотрения пары концентрических шестиугольники, в отличие от пары кругов. Представляя это шестиугольное колесо, «катящееся» по поверхности, Галилей замечает, что внутренний шестиугольник «прыгает» на небольшое пространство с каждым перекатом внешнего шестиугольника на новую грань.^[5] Затем он представляет, что произойдет в пределе, когда число граней многоугольника станет очень большим, и обнаружит, что небольшое пространство, которое «перепрыгивает» внутренний многоугольник, становится все меньше и меньше, и пишет:

Следовательно, больший многоугольник, имеющий тысячу сторон, проходит и измеряет прямую линию, равную его периметру, в то время как в то же время меньший многоугольник проходит примерно такую же линию, но непрерывно составленную из тысячи маленьких частиц, равных тысяче сторон с вставлены тысячи маленьких пустот - мы можем назвать их «пустотой» по отношению к тысячам строк, которых касаются стороны многоугольника.^[5]

Поскольку круг - это всего лишь предел, при котором количество граней многоугольника становится бесконечным, Галилей обнаруживает, что колесо Аристотеля содержит материал, заполненный бесконечно малыми пространствами или «пустотами», и что «промежуточные пустоты не измеряются количественно, но бесконечно много".^[5] Это приводит Галилея к выводу, что вера в атомы в том смысле, что материя «состоит из бесконечно большого числа атомов, не поддающихся количественной оценке», достаточна для решения проблемы колеса.^[5]Жиль де Роберваль (Personne) 1602–1675 также связан с этой проблемой.

В 19 веке

Бернар Больцано обсуждал колесо Аристотеля в Парадоксы бесконечного (1851), книга, оказавшая влияние Георг Кантор и последующие мыслители о математике бесконечности. Больцано отмечает, что существует биекция между точками любых двух подобных дуг, что может быть реализовано путем рисования радиуса, отмечая, что история этого явно парадоксального факта восходит к Аристотелю.^[1]

В 20 веке

Автор Математические заблуждения и парадоксы В качестве модели парадокса использует монету, приклеенную к полдоллару с выровненными центрами, и оба они прикреплены к оси. Дайм служит меньшим кружком, а полдоллара - большим. Он написал:

Таким образом, это решение или ключ к нему. Хотя вы следите за тем, чтобы полдоллара не соскользнул по столешнице, «точка», отслеживающая отрезок линии у основания десятицентовой монеты, постоянно вращается и скользит. Он скользит по отношению к столешнице. Поскольку десятицентовик не касается столешницы, вы не заметите скольжения. Если вы можете катать полдоллара по столу и в то же время катать десятицентовик (или, еще лучше, ось) по деревянному бруску, вы действительно можете наблюдать скольжение. Если вы когда-либо парковались слишком близко к бордюру, вы заметили визг, издаваемый колпаком, когда он скользит (и катится) по бордюру, в то время как ваша шина просто катится по тротуару. Чем меньше маленький круг относительно большого, тем больше маленький кружится. Конечно, центр двух кругов вообще не вращается, поэтому он скользит полностью.^[6]

В качестве альтернативы можно отказаться от предположения, что меньший круг не зависит от большего круга. Представьте себе шину как больший круг, а меньший круг - как внутреннюю окружность шины, а не как обод. Движение внутреннего круга зависит от большего круга. Таким образом, его перемещение из любой точки в другую можно рассчитать, используя обратное их отношение.

Анализ и решения

Парадокс в том, что меньший внутренний круг перемещается на 2πр, длина окружности большего внешнего круга радиуса р, а не его собственная окружность. Если бы внутренний круг катался отдельно, он переместился бы на 2πр, его собственная окружность с радиусом р. Внутренний круг не обособлен, а жестко связан с большим. Итак, 2πр это отвлекающий маневр. Центр внутреннего круга имеет значение, его радиус важен, а длина окружности - нет.

Первое решение

Если меньший круг зависит от большего (случай I), то движение большего круга заставляет меньший круг пересекать окружность большего круга. Если больший круг зависит от меньшего (Случай II), то движение меньшего круга заставляет больший круг пересекать окружность меньшего круга. Это самое простое решение.

Второе решение

Это решение учитывает переход от начальной позиции к конечной. Пусть Pb будет точкой на большем круге, а Ps будет точкой на меньшем круге, обе на одном радиусе. Для удобства предположим, что они обе находятся прямо под центром, аналогично тому, как обе стрелки часов указывают на шесть. И Pb, и Ps перемещаются циклоида путь, как они катятся вместе один оборот. Здесь изображены два пути: http://mathworld.wolfram.com/Cycloid.html и http://mathworld.wolfram.com/CurtateCycloid.html.

Пока каждый едет 2πр по горизонтали от начала до конца циклоидный путь Ps короче и эффективнее, чем путь Pb. Pb движется выше и ниже пути центра - единственного прямого - чем Ps. На изображении рядом показаны круги до и после одного оборота. Он показывает движения центра Pb и Ps, причем Pb и Ps начинаются и заканчиваются в верхней части их кругов. Зеленая пунктирная линия - это движение центра. Синяя штриховая кривая показывает движение Pb. Красная штриховая кривая показывает движение Пс. Путь Ps явно короче, чем у Pb. Чем ближе точка Ps к центру, тем короче, прямее и ближе к зеленой линии ее путь.

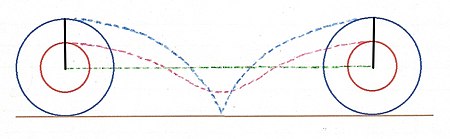
Если бы Pb и Ps были где-нибудь еще на своих кругах, изогнутые пути были бы одинаковой длины. Подводя итог, меньший круг движется по горизонтали на 2πр потому что любая точка на меньшем круге проходит более короткий и прямой путь, чем любая точка на большом круге.

Третье решение

Это решение сравнивает только начальную и конечную позиции. У большего круга и меньшего круга один и тот же центр. Если указанный центр перемещается, оба круга перемещаются на одинаковое расстояние, что является необходимым свойством перевод и равно 2πр в эксперименте. Кроме того, все остальные точки на обоих кругах имеют одинаковое положение относительно центра до и после прокатки одного оборота (или любого другого целого числа оборотов).

Смотрите также

Кривая брахистохрона

дальнейшее чтение

[:0-1] а ^б ^c ^d ^е ^ж ^грамм Драбкин, Израиль Э. (1950). "Колесо Аристотеля: Заметки об истории парадокса". Осирис. 9: 162–198. Дои:10.1086/368528. JSTOR 301848.

[2] Леувен, Джойс ван (2016-03-17). Аристотелевская механика: текст и диаграммы. Springer. ISBN 9783319259253.

[3] Кардано, Джеронимо (1570). Opus novum de ratioibus numerorum ...: Praeterea Artis magnae sive de Regulis algebraicis liber un ... Item De regula liber ...

[4] Мерсенн, Марин (1623). Quaestiones celeberrimae в Genesim ... (на латыни).

[:1-5] а ^б ^c ^d Галилей, Галилей; Дрейк, Стиллман (2000). Две новые науки: центры тяжести и сила удара. Wall & Emerson. ISBN 9780921332503.

[6] Букет, Брайан Х. (1982). Математические заблуждения и парадоксы. Ван Ностранд Рейнхольд. С. 3–9. ISBN 0-442-24905-5.

[1]

[2]

[3]

[4]

[5]

[6]