Закон Ома - Ohms law

Закон Ома заявляет, что Текущий через дирижер между двумя точками находится прямо пропорциональный к Напряжение через две точки. Вводя константу пропорциональности, сопротивление,[1] мы приходим к обычному математическому уравнению, описывающему эту связь:[2]
куда я ток через проводник в единицах амперы, V измеренное напряжение через проводник в единицах вольт, и р это сопротивление проводника в единицах Ом. В частности, закон Ома гласит, что р в этом отношении постоянно, независимо от тока.[3] Закон Ома - это эмпирическое отношение что точно описывает проводимость подавляющего большинства электропроводящие материалы на многие порядки величины тока. Однако некоторые материалы не подчиняются закону Ома, их называют неомический.
Закон назван в честь немецкого физика. Георг Ом, который в трактате, опубликованном в 1827 году, описал измерения приложенного напряжения и тока через простые электрические цепи, содержащие провода различной длины. Ом объяснил свои экспериментальные результаты немного более сложным уравнением, чем современная форма, приведенная выше (см. § История ниже).
В физике термин Закон Ома также используется для обозначения различных обобщений закона; например вектор форма закона, используемая в электромагнетизм и материаловедение:
куда J это плотность тока в заданном месте в резистивном материале, E электрическое поле в этом месте, и σ (сигма ) - это зависящий от материала параметр, называемый проводимость. Эта переформулировка закона Ома связана с Густав Кирхгоф.[4]
История

В январе 1781 г. Георг Ом работа, Генри Кавендиш экспериментировал с Лейденские банки и стеклянные трубки разного диаметра и длины, наполненные солевым раствором. Он измерил ток, отметив, насколько сильное потрясение он почувствовал, замыкая цепь своим телом. Кавендиш писал, что «скорость» (ток) напрямую зависит от «степени электризации» (напряжения). В то время он не сообщал свои результаты другим ученым,[5] и его результаты были неизвестны до Максвелл опубликовал их в 1879 г.[6]
Фрэнсис Рональдс обозначены «интенсивность» (напряжение) и «количество» (ток) для сухой ворс - источник высокого напряжения - в 1814 г. с использованием электрометр с позолотой. Он обнаружил, что для сухой сваи соотношение между двумя параметрами не было пропорциональным при определенных метеорологических условиях.[7][8]
Ом работал над сопротивлением в 1825 и 1826 годах и опубликовал свои результаты в 1827 году в виде книги. Die galvanische Kette, Mathematisch Bearbeitet («Гальваническая цепь исследована математически»).[9] Он черпал вдохновение из Фурье работа по теплопроводности в теоретическом объяснении своей работы. Для экспериментов он изначально использовал гальванические сваи, но позже использовал термопара поскольку это обеспечивало более стабильный источник напряжения с точки зрения внутреннего сопротивления и постоянного напряжения. Он использовал гальванометр для измерения тока и знал, что напряжение между выводами термопары пропорционально температуре перехода. Затем он добавил испытательные провода различной длины, диаметра и материала, чтобы замкнуть цепь. Он обнаружил, что его данные можно смоделировать с помощью уравнения
куда Икс было чтение из гальванометр, л была длина испытательного проводника, а зависит от температуры спая термопары, а б была константой всей установки. Исходя из этого, Ом определил свой закон пропорциональности и опубликовал свои результаты.
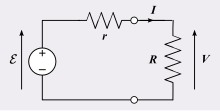
В современных обозначениях мы бы написали,
куда разомкнутый ЭДС термопары, это внутреннее сопротивление термопары и сопротивление испытательного провода. С точки зрения длины провода это становится
куда сопротивление испытательного провода на единицу длины. Таким образом, коэффициенты Ома равны,

Закон Ома был, вероятно, самым важным из первых количественных описаний физики электричества. Сегодня мы считаем это почти очевидным. Когда Ом впервые опубликовал свою работу, это было не так; критики отнеслись к его трактовке предмета враждебно. Его работы называли «паутиной голых фантазий».[10] а министр образования Германии провозгласил, что «профессор, проповедовавший такие ереси, недостоин преподавать науку».[11] Преобладающая в то время научная философия в Германии утверждала, что эксперименты не обязательно проводить для развития понимания природы, потому что природа так хорошо организована, и что научные истины можно вывести только с помощью рассуждений.[12] Кроме того, брат Ома Мартин, математик, боролся с немецкой системой образования. Эти факторы препятствовали принятию работ Ома, и его работы не получили широкого признания до 1840-х годов. Однако Ом получил признание за свой вклад в науку задолго до своей смерти.
В 1850-х годах закон Ома был известен как таковой и широко считался доказанным, и альтернативы, такие как "Закон Барлоу ", были дискредитированы с точки зрения реальных приложений для проектирования телеграфных систем, как это обсуждалось Сэмюэл Ф. Б. Морс в 1855 г.[13]
В электрон был открыт в 1897 году Дж. Дж. Томсон, и быстро поняли, что это частица (носитель заряда ), несущий электрические токи в электрических цепях. В 1900 г. первый (классический ) модель электропроводности, Модель Друде, был предложен Пол Друде, что наконец дало научное объяснение закону Ома. В этой модели твердый проводник состоит из неподвижной решетки из атомы (ионы ), с электроны проводимости перемещаясь в нем беспорядочно. Напряжение на проводнике вызывает электрическое поле, который ускоряет электроны в направлении электрического поля, вызывая дрейф электронов, который представляет собой электрический ток. Однако электроны сталкиваются и разлетаются с атомами, что приводит к хаотическому их движению, преобразуя кинетическую энергию, добавленную к электрону полем, в высокая температура (тепловая энергия ). Используя статистические распределения, можно показать, что средняя скорость дрейфа электронов и, следовательно, ток пропорциональны электрическому полю и, следовательно, напряжению в широком диапазоне напряжений.
Развитие квантовая механика в 1920-х годах эта картина несколько изменилась, но в современных теориях можно показать, что средняя дрейфовая скорость электронов пропорциональна электрическому полю, таким образом выводя закон Ома. В 1927 г. Арнольд Зоммерфельд применил квантовую Распределение Ферми-Дирака энергии электронов к модели Друде, в результате чего модель свободных электронов. Год спустя, Феликс Блох показал, что электроны движутся волнообразно (Блоховские электроны ) через твердую кристаллическую решетку, поэтому рассеяние на атомах решетки, как постулируется в модели Друде, не является важным процессом; электроны разлетаются на примесные атомы и дефекты материала. Последний преемник, современный квантовый ленточная теория твердых тел, показал, что электроны в твердом теле не могут принимать никакой энергии, как предполагается в модели Друде, но ограничены энергетическими зонами с промежутками между ними энергий, которые электронам запрещено иметь. Размер запрещенной зоны является характеристикой конкретного вещества, которая имеет прямое отношение к его удельному электрическому сопротивлению, что объясняет, почему некоторые вещества электрические проводники, немного полупроводники, и немного изоляторы.
В то время как старый термин для обозначения электропроводности, Мхо (инверсия единицы сопротивления Ом), все еще используется, новое имя, Сименс, принят на вооружение в 1971 г. Эрнст Вернер фон Сименс. Сименс предпочтительнее в официальных документах.
В 1920-х годах было обнаружено, что ток, проходящий через практический резистор, на самом деле имеет статистические колебания, которые зависят от температуры, даже когда напряжение и сопротивление точно постоянны; это колебание, теперь известное как Шум Джонсона – Найквиста, обусловлено дискретным характером заряда. Этот тепловой эффект означает, что измерения тока и напряжения, которые проводятся в течение достаточно коротких периодов времени, дадут отношения V / I, которые колеблются от значения R, подразумеваемого средним по времени или средний по ансамблю измеренного тока; Закон Ома остается верным для среднего тока в случае обычных резистивных материалов.
Работа Ома задолго до Уравнения Максвелла и любое понимание частотно-зависимых эффектов в цепях переменного тока. Современные разработки в теории электромагнетизма и теории цепей не противоречат закону Ома, когда они оцениваются в соответствующих пределах.
Объем
Закон Ома - это эмпирический закон, обобщение многих экспериментов, которые показали, что ток примерно пропорционален электрическому полю для большинства материалов. Это менее фундаментально, чем Уравнения Максвелла и не всегда соблюдается. Любой данный материал будет авария в достаточно сильном электрическом поле, а некоторые материалы, представляющие интерес для электротехники, «неомичны» в слабых полях.[14][15]
Закон Ома соблюдается в широком диапазоне масштабов длины. В начале 20 века считалось, что закон Ома не выдержит атомный масштаб, но эксперименты не подтвердили этого ожидания. По состоянию на 2012 год исследователи продемонстрировали, что закон Ома работает для кремний провода размером четыре атома в ширину и один атом в высоту.[16]
Микроскопическое происхождение

Зависимость плотности тока от приложенного электрического поля существенно квантово-механический в природе; (см. Классическая и квантовая проводимость.) Качественное описание, приводящее к закону Ома, может быть основано на классическая механика с использованием Модель Друде разработан Пол Друде в 1900 г.[17][18]
Модель Друде рассматривает электроны (или другие носители заряда), такие как шарики для игры в пинбол, прыгающие ионы которые составляют структуру материала. Электроны будут ускорены в направлении, противоположном электрическому полю, за счет среднего электрического поля в их местоположении. Однако при каждом столкновении электрон отклоняется в случайном направлении со скоростью, намного превышающей скорость, набираемую электрическим полем. В результате электроны движутся по зигзагообразному пути из-за столкновений, но обычно дрейфуют в направлении, противоположном электрическому полю.
В скорость дрейфа затем определяет электрическую плотность тока и его отношение к E и не зависит от столкновений. Друде рассчитал среднюю скорость дрейфа из п = −еEτ куда п это средний импульс, −е - заряд электрона, τ - среднее время между столкновениями. Поскольку и импульс, и плотность тока пропорциональны скорости дрейфа, плотность тока становится пропорциональной приложенному электрическому полю; это приводит к закону Ома.
Гидравлическая аналогия
А гидравлическая аналогия иногда используется для описания закона Ома. Давление воды, измеренное паскали (или же PSI ), является аналогом напряжения, потому что установление разницы давлений воды между двумя точками вдоль (горизонтальной) трубы заставляет воду течь. Расход воды, как в литры в секунду, является аналогом тока, как в кулоны в секунду. Наконец, ограничители потока, такие как отверстия в трубах между точками измерения давления воды, являются аналогом резисторов. Мы говорим, что скорость потока воды через ограничитель диафрагмы пропорциональна разнице давления воды на ограничителе. Точно так же скорость протекания электрического заряда, то есть электрического тока, через электрический резистор пропорциональна разнице напряжений, измеренных на резисторе.
Переменные расхода и давления могут быть рассчитаны в гидродинамической сети с использованием аналогии гидравлического сопротивления.[19][20] Метод может применяться как в условиях установившегося, так и в переходном режиме потока. В линейном ламинарный поток область, край, Закон Пуазейля описывает гидравлическое сопротивление трубы, но в турбулентный поток В этой области зависимости давление – расход становятся нелинейными.
Гидравлическая аналогия с законом Ома использовалась, например, для приблизительного определения кровотока в системе кровообращения.[21]
Анализ схемы
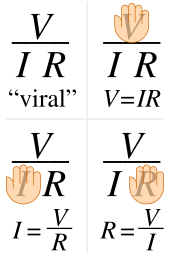
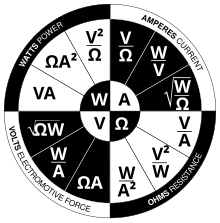
В анализ схем, три эквивалентных выражения закона Ома используются как синонимы:
Каждое уравнение цитируется некоторыми источниками как определяющее соотношение закона Ома,[2][22][23]или все три цитируются,[24] или полученный из пропорциональной формы,[25]или даже два, которые не соответствуют исходному утверждению Ома, могут иногда быть указаны.[26][27]
Взаимозаменяемость уравнения можно представить в виде треугольника, где V (Напряжение ) размещается в верхней части, я (Текущий ) помещается в левую секцию, а р (сопротивление ) находится справа. Разделитель между верхней и нижней частями обозначает деление (отсюда и полоса деления).
Резистивные схемы
Резисторы элементы схемы, препятствующие прохождению электрический заряд в соответствии с законом Ома и рассчитаны на определенное значение сопротивления р. На принципиальных схемах резистор показан в виде длинного прямоугольника или зигзагообразного символа. Элемент (резистор или проводник), который ведет себя в соответствии с законом Ома в некотором рабочем диапазоне, называется омическое устройство (или омический резистор), поскольку закона Ома и одного значения сопротивления достаточно, чтобы описать поведение устройства в этом диапазоне.
Закон Ома справедлив для цепей, содержащих только резистивные элементы (без емкости или индуктивности) для всех форм управляющего напряжения или тока, независимо от того, являются ли управляющее напряжение или ток постоянными (ОКРУГ КОЛУМБИЯ ) или изменяющиеся во времени, например AC. В любой момент времени для таких цепей действует закон Ома.
Резисторы в серии или в параллельно могут быть сгруппированы в одно «эквивалентное сопротивление», чтобы применить закон Ома при анализе схемы.
Реактивные цепи с изменяющимися во времени сигналами
Когда реактивные элементы, такие как конденсаторы, катушки индуктивности или линии передачи, включены в цепь, к которой приложено переменное или изменяющееся во времени напряжение или ток, соотношение между напряжением и током становится решением проблемы. дифференциальное уравнение, поэтому закон Ома (как определено выше) не применяется напрямую, поскольку эта форма содержит только сопротивления, имеющие значение р, а не комплексные импедансы, которые могут содержать емкость (C) или индуктивность (L).
Уравнения для неизменный во времени AC схемы принимают ту же форму, что и закон Ома. Однако переменные обобщаются на сложные числа а формы сигналов тока и напряжения комплексные экспоненты.[28]
В этом подходе форма волны напряжения или тока принимает вид Aeул, куда т время, s - комплексный параметр, а А - комплексный скаляр. В любом линейная инвариантная во времени система, все токи и напряжения могут быть выражены одним и тем же s параметр в качестве входных данных для системы, позволяющий исключить изменяющийся во времени комплексный экспоненциальный член и описать систему алгебраически в терминах комплексных скаляров в формах сигналов тока и напряжения.
Сложное обобщение сопротивления есть сопротивление, обычно обозначается Z; можно показать, что для индуктора
а для конденсатора
Теперь мы можем написать,
куда V и я - комплексные скаляры по напряжению и току соответственно и Z - комплексный импеданс.
Эта форма закона Ома с Z заняв место р, обобщает более простой вид. Когда Z сложная, за рассеивание тепла отвечает только реальная часть.
В общей цепи переменного тока, Z сильно зависит от частотного параметра s, а также соотношение между напряжением и током.
Для обычного случая устойчивого синусоида, то s параметр принимается равным , соответствующая сложной синусоиде . Реальные части таких сложных форм сигналов тока и напряжения описывают фактические синусоидальные токи и напряжения в цепи, которые могут находиться в разных фазах из-за различных комплексных скаляров.
Линейные приближения
Закон Ома - одно из основных уравнений, используемых в анализ электрических цепей. Это касается как металлических проводников, так и компонентов схем (резисторы ) специально для этого поведения. Оба широко используются в электротехнике. Материалы и компоненты, подчиняющиеся закону Ома, называются «омическими».[29] что означает, что они производят одинаковое значение сопротивления (р = V/я) независимо от значения V или же я который применяется и независимо от того, является ли приложенное напряжение или ток постоянным (постоянный ток ) положительной или отрицательной полярности или переменного тока (переменный ток ).
В истинно омическом устройстве такое же значение сопротивления будет рассчитано из р = V/я независимо от величины подаваемого напряжения V. То есть соотношение V/я постоянна, а когда ток отображается как функция напряжения, кривая линейный (прямая линия). Если напряжение повышено до некоторого значения V, то это напряжение V деленный на измеренный ток я будет равно р. Или если ток принудительно установлен на какое-то значение я, то измеренное напряжение V делится на этот текущий я это также р. Поскольку сюжет я против V прямая линия, то также верно, что для любого набора двух разных напряжений V1 и V2 применяется к данному устройству сопротивления р, производящие токи я1 = V1/р и я2 = V2/р, что отношение (V1 − V2)/(я1 − я2) также является константой, равной р. Оператор «дельта» (Δ) используется для обозначения разницы в величине, поэтому мы можем написать ΔV = V1 − V2 и Δя = я1 − я2. Подводя итог, для любого действительно омического устройства, имеющего сопротивление р, V/я = ΔV/ Δя = р для любого приложенного напряжения или тока или для разницы между любым набором приложенных напряжений или токов.

Однако есть компоненты электрических цепей, которые не подчиняются закону Ома; то есть их соотношение между током и напряжением (их я–V изгиб ) является нелинейный (или неомический). Примером может служить p – n-переходный диод (кривая справа). Как видно на рисунке, ток не увеличивается линейно с приложенным напряжением на диоде. Можно определить значение тока (я) для заданного значения приложенного напряжения (V) по кривой, но не по закону Ома, поскольку значение «сопротивления» не является постоянным в зависимости от приложенного напряжения. Кроме того, ток значительно увеличивается, только если приложенное напряжение положительное, а не отрицательное. Соотношение V/я для некоторой точки вдоль нелинейной кривой иногда называют статический, или же хордовый, или же ОКРУГ КОЛУМБИЯ, сопротивление,[30][31] но, как видно на рисунке, значение общей V в целом я изменяется в зависимости от конкретной точки выбранной нелинейной кривой. Это означает, что «сопротивление постоянному току» V / I в некоторой точке кривой не такое, как то, что можно было бы определить, подавая сигнал переменного тока с максимальной амплитудой Δ.V вольт или Δя ампер с центром в той же точке на кривой и измерением ΔV/ Δя. Однако в некоторых диодных приложениях сигнал переменного тока, подаваемый на устройство, невелик, и можно проанализировать схему с точки зрения динамичный, слабосигнальный, или же добавочный сопротивление, определяемое как сопротивление по наклону V–я кривая при среднем значении (рабочая точка постоянного тока) напряжения (т. е. производная тока по напряжению). Для достаточно слабых сигналов динамическое сопротивление позволяет рассчитать сопротивление малого сигнала по закону Ома как приблизительно единицу по наклону линии, проведенной по касательной к V–я кривая в рабочей точке постоянного тока.[32]
Температурные эффекты
Закон Ома иногда формулируется так: «Для проводника в данном состоянии электродвижущая сила пропорциональна производимому току». То есть, что сопротивление, соотношение приложенных электродвижущая сила (или напряжение) к току, «не зависит от силы тока». Квалификатор «в данном состоянии» обычно интерпретируется как означающий «при постоянной температуре», поскольку удельное сопротивление материалов обычно зависит от температуры. Поскольку проводимость тока связана с Джоулевое нагревание проводящего органа, согласно Первый закон Джоуля температура проводящего тела может измениться, когда по нему протекает ток. Таким образом, зависимость сопротивления от температуры делает сопротивление зависимым от тока в типичной экспериментальной установке, что затрудняет прямую проверку закона в такой форме. Максвелл и другие разработали несколько методов экспериментальной проверки закона в 1876 году, контролируя эффекты нагрева.[33]
Отношение к теплопроводности
Принцип Ома предсказывает течение электрического заряда (т. Е. Тока) в электрических проводниках, когда они подвергаются влиянию разности напряжений; Жан-Батист-Жозеф Фурье принцип предсказывает поток высокая температура в теплопроводах при воздействии перепада температур.
Одно и то же уравнение описывает оба явления, причем переменные уравнения в обоих случаях имеют разный смысл. В частности, решение задачи теплопроводности (Фурье) с температура (движущая "сила") и поток тепла (скорость потока ведомого "количества", то есть тепловой энергии) также решает аналогичный электрическая проводимость (Ом) проблема с электрический потенциал (движущая "сила") и электрический ток (скорость потока ведомого «количества», т.е. заряда) переменные.
В основе работы Фурье лежало его ясное понимание и определение теплопроводность. Он предположил, что, при прочих равных, поток тепла строго пропорционален градиенту температуры. Хотя это, несомненно, верно для малых температурных градиентов, строго пропорциональное поведение будет потеряно, когда реальные материалы (например, имеющие теплопроводность, которая является функцией температуры) подвергаются большим температурным градиентам.
Аналогичное предположение делается в формулировке закона Ома: при прочих равных, сила тока в каждой точке пропорциональна градиенту электрического потенциала. Правильность предположения о том, что поток пропорционален градиенту, легче проверить с использованием современных методов измерения для электрического случая, чем для теплового случая.
Другие версии
Закон Ома в приведенной выше форме является чрезвычайно полезным уравнением в области электротехники и электроники, поскольку он описывает, как напряжение, ток и сопротивление взаимосвязаны на «макроскопическом» уровне, то есть обычно как элементы схемы в электрическая цепь. Физики, изучающие электрические свойства вещества на микроскопическом уровне, используют тесно связанный и более общий вектор уравнение, иногда также называемое законом Ома, имеющее переменные, которые тесно связаны с V, I и R скаляр переменные закона Ома, но каждая из которых является функцией положения внутри проводника. Физики часто используют эту форму континуума закона Ома:[34]
куда "E" это электрическое поле вектор с единицами измерения вольт на метр (аналог "V" закона Ома, который имеет единицы измерения вольт), "J" это плотность тока вектор с единицами измерения ампер на единицу площади (аналог «I» закона Ома, в котором есть единицы измерения ампер), а «ρ» (греческое «ро») - это удельное сопротивление с единицами измерения Ом · метр (аналог «R» закона Ома, который имеет единицы измерения Ом). Вышеприведенное уравнение иногда записывают[35] в качестве J = E где «σ» (греч. «сигма») - проводимость что является обратной величиной ρ.

Напряжение между двумя точками определяется как:[36]
с элемент пути по интегрированию вектора электрического поля E. Если применяется E поле однородно и ориентировано по длине проводника, как показано на рисунке, затем определяют напряжение V в обычном соглашении о том, что оно противоположно направлению поля (см. рисунок), и с пониманием того, что напряжение V измеряется дифференциально. по всей длине проводника, позволяя опустить символ Δ, приведенное выше векторное уравнение сводится к скалярному уравнению:
Поскольку E поле однородно в направлении длины провода, для проводника, имеющего равномерно постоянное удельное сопротивление ρ, плотность тока J также будет однородным в любой площади поперечного сечения и ориентированным в направлении длины провода, поэтому мы можем написать:[37]
Подставляя вышеуказанные 2 результата (для E и J соответственно) в форму континуума, показанную в начале этого раздела:
В электрическое сопротивление однородного проводника дается через удельное сопротивление к:[37]
куда л длина проводника в SI единицы метров, а - площадь поперечного сечения (для круглого провода а = πr2 если р радиус) в метрах в квадрате, а ρ - удельное сопротивление в Ом · метрах.
После замены р из приведенного выше уравнения в уравнение, предшествующее ему, непрерывная форма закона Ома для однородного поля (и постоянной плотности тока), ориентированного по длине проводника, сводится к более знакомой форме:
Совершенная кристаллическая решетка с достаточно низким тепловым движением и без отклонений от периодической структуры не имела бы удельное сопротивление,[38] но настоящий металл имеет кристаллографические дефекты, примеси, кратные изотопы, и тепловое движение атомов. Электроны разбросать от всего этого, что приводит к сопротивлению их потоку.
Более сложные обобщенные формы закона Ома важны для физика конденсированного состояния, который изучает свойства иметь значение и, в частности, его электронная структура. В широком смысле они подпадают под тему основные уравнения и теория транспортные коэффициенты.
Магнитные эффекты
Если внешний B-поле присутствует, и проводник не в покое, а движется со скоростью v, то необходимо добавить дополнительный член для учета тока, индуцированного Сила Лоренца на носителях заряда.
в рама отдыха подвижного проводника этот член выпадает, потому что v= 0. Противоречия нет, поскольку электрическое поле в системе покоя отличается от E-поле в рамке лаборатории: E ′ = E + v×B.Электрическое и магнитное поля относительны, см. Преобразование Лоренца.
Если нынешний J чередуется из-за приложенного напряжения или E-поле изменяется во времени, тогда к сопротивлению необходимо прибавить реактивное сопротивление, чтобы учесть самоиндуктивность, см. электрический импеданс. Реактивное сопротивление может быть большим, если частота высока или проводник скручен.
Проводящие жидкости
В проводящей жидкости, такой как плазма, есть аналогичный эффект. Рассмотрим жидкость, движущуюся со скоростью в магнитном поле . Относительное движение индуцирует электрическое поле который оказывает электрическая сила на заряженных частицах, вызывающих электрический ток . Уравнение движения электронного газа с числовая плотность , записывается как
куда , и - заряд, масса и скорость электронов соответственно. Также, - частота столкновений электронов с ионами, имеющими поле скорости . Поскольку масса электрона очень мала по сравнению с массой ионов, мы можем игнорировать левую часть приведенного выше уравнения и записать
где мы использовали определение плотность тока, а также положить какой электрическая проводимость. Это уравнение может быть также записано в виде
куда это удельное электрическое сопротивление. Также принято писать вместо что может сбивать с толку, поскольку это те же обозначения, что и для коэффициента магнитной диффузии, определяемого как .
Смотрите также
- Закон диффузии Фика
- Закон Гопкинсона («Закон Ома для магнетизма»)
- Теорема о передаче максимальной мощности
- Теорема Нортона
- Листовое сопротивление
- Теорема суперпозиции
- Тепловой шум
- Теорема Тевенина
Рекомендации
- ^ Консоливер, Эрл Л. и Митчелл, Гровер И. (1920). Автомобильные системы зажигания. Макгроу-Хилл. п.4.
сопротивление тока пропорционально напряжению по закону Ома.
- ^ а б Роберт А. Милликен и Э. С. Бишоп (1917). Элементы электричества. Американское техническое общество. п.54.
По закону Ома ток прямо пропорционален.
- ^ Оливер Хевисайд (1894). Электрооборудование. 1. Macmillan and Co. стр. 283. ISBN 978-0-8218-2840-3.
- ^ Оливье Дарриголь, Электродинамика от Ампера до Эйнштейна, п. 70, Oxford University Press, 2000 г. ISBN 0-19-850594-9.
- ^ Флеминг, Джон Эмброуз (1911). . В Чисхолме, Хью (ред.). Британская энциклопедия. 9 (11-е изд.). Издательство Кембриджского университета. п. 182.
- ^ Сэнфорд П. Бордо (1982) Вольт в Герц ... Рост электричества. Издательство Burgess, Миннеаполис, Миннесота. стр. 86–107, ISBN 0-8087-4908-0
- ^ Рональдс, Б. Ф. (2016). Сэр Фрэнсис Рональдс: отец электрического телеграфа. Лондон: Imperial College Press. ISBN 978-1-78326-917-4.
- ^ Рональдс, Б. Ф. (июль 2016 г.). «Фрэнсис Рональдс (1788–1873): первый инженер-электрик?». Труды IEEE. 104 (7): 1489–1498. Дои:10.1109 / JPROC.2016.2571358. S2CID 20662894.
- ^ Г. С. Ом (1827). Die galvanische Kette, Mathematisch Bearbeitet (PDF). Берлин: Т. Х. Риман. Архивировано из оригинал (PDF) 26 марта 2009 г.
- ^ Дэвис, Б., «Сеть обнаженных фантазий?», Физическое образование 15 57–61, Институт физики, выпуск 1, январь 1980 г. [1]
- ^ Харт, И.Б., Создатели науки, Лондон, Oxford University Press, 1923. стр. 243. [2]
- ^ Герберт Шнедельбах, Философия в Германии 1831–1933 гг., стр. 78–79, Cambridge University Press, 1984. ISBN 0521296463.
- ^ Талиаферро Престон (1855). Товарищ по телеграфу Шаффнера: посвященный науке и искусству телеграфа Морзе. Том 2. Падни и Рассел.
- ^ Перселл, Эдвард М. (1985), Электричество и магнетизм, Курс физики Беркли, 2 (2-е изд.), McGraw-Hill, p. 129, ISBN 978-0-07-004908-6
- ^ Гриффитс, Дэвид Дж. (1999), Введение в электродинамику (3-е изд.), Прентис Холл, стр.289, ISBN 978-0-13-805326-0
- ^ Вебер, Б .; Mahapatra, S .; Ryu, H .; Lee, S .; Фюрер, А .; Reusch, T. C. G .; Томпсон, Д. Л .; Lee, W. C. T .; Klimeck, G .; Холленберг, Л. К. Л .; Симмонс, М. Ю. (2012). «Закон Ома выживает до атомных масштабов». Наука. 335 (6064): 64–67. Bibcode:2012Наука ... 335 ... 64Вт. Дои:10.1126 / наука.1214319. PMID 22223802. S2CID 10873901.
- ^ Друде, Пол (1900). "Zur Elektronentheorie der Metalle". Annalen der Physik. 306 (3): 566–613. Bibcode:1900АнП ... 306..566Д. Дои:10.1002 / andp.19003060312.[мертвая ссылка ]
- ^ Друде, Пол (1900). "Zur Elektronentheorie der Metalle; II. Teil. Galvanomagnetische und thermomagnetische Effecte". Annalen der Physik. 308 (11): 369–402. Bibcode:1900АнП ... 308..369Д. Дои:10.1002 / andp.19003081102.[мертвая ссылка ]
- ^ А. Акерс; М. Гассман и Р. Смит (2006). Анализ гидравлической системы питания. Нью-Йорк: Тейлор и Фрэнсис. Глава 13. ISBN 978-0-8247-9956-4.
- ^ А. Эспозито, "Упрощенный метод анализа схем по аналогии", Дизайн машины, Октябрь 1969 г., стр. 173–177.
- ^ Гайтон, Артур; Холл, Джон (2006). «Глава 14: Обзор кровообращения; медицинская физика давления, потока и сопротивления». В Gruliow, Ребекка (ред.). Учебник медицинской физиологии (11-е изд.). Филадельфия, Пенсильвания: Elsevier Inc., стр. 164. ISBN 978-0-7216-0240-0.
- ^ Джеймс Уильям Нильссон и Сьюзан А. Ридель (2008). Электрические схемы. Прентис Холл. п. 29. ISBN 978-0-13-198925-2.
- ^ Элвин М. Халперн и Эрих Эрлбах (1998). Очерк теории и проблемы начальной физики Шаума II. McGraw-Hill Professional. п. 140. ISBN 978-0-07-025707-8.
- ^ Дейл Р. Патрик и Стивен В. Фардо (1999). Понимание цепей постоянного тока. Newnes. п. 96. ISBN 978-0-7506-7110-1.
- ^ Томас О'Конор Слоан (1909). Элементарные электрические расчеты. D. Van Nostrand Co. с.41.
R = пропорциональный закон Ома.
- ^ Линней Камминг (1902). Электричество обработано экспериментально для использования школ и студентов. Longman's Green and Co. стр.220.
V = закон IR Ома.
- ^ Бенджамин Штайн (1997). Строительная техника (2-е изд.). Джон Уайли и сыновья. п. 169. ISBN 978-0-471-59319-5.
- ^ Раджендра Прасад (2006). Основы электротехники. Прентис-холл Индии. ISBN 978-81-203-2729-0.
- ^ Хьюз, Э, Электрические технологии, стр. 10, Longmans, 1969.
- ^ Форбс Т. Браун (2006). Динамика инженерных систем. CRC Press. п. 43. ISBN 978-0-8493-9648-9.
- ^ Кеннет Л. Кайзер (2004). Справочник по электромагнитной совместимости. CRC Press. С. 13–52. ISBN 978-0-8493-2087-3.
- ^ Горовиц, Пол; Winfield Hill (1989). Искусство электроники (2-е изд.). Издательство Кембриджского университета. п. 13. ISBN 978-0-521-37095-0.
- ^ Нормальный Локьер, изд. (21 сентября 1876 г.). "Отчеты". Природа. Macmillan Journals Ltd. 14 (360): 451–459 [452]. Bibcode:1876Натура..14..451.. Дои:10.1038 / 014451a0.
- ^ Лернер, Лоуренс С. (1977). Физика для ученых и инженеров. Джонс и Бартлетт. п. 736. ISBN 978-0-7637-0460-5.
- ^ Сеймур Дж. Физическая электроника, Питман, 1972, с. 53–54.
- ^ Лернер Л, Физика для ученых и инженеров, Джонс и Бартлетт, 1997, стр. 685–686
- ^ а б Лернер Л, Физика для ученых и инженеров, Джонс и Бартлетт, 1997, стр. 732–733
- ^ Сеймур Дж. Физическая электроника, стр. 48–49, Питман, 1972
Внешние ссылки и дальнейшее чтение
- Закон Ома глава из Уроки в электрических цепях Том 1 DC книга и серии.
- Джон С. Шедд и Мэйо Д. Херши,«История закона Ома», Популярная наука, Декабрь 1913 г., стр. 599–614, Bonnier Corporation ISSN 0161-7370, дает историю исследований Ома, предшествующие работы, ложное уравнение Ома в первой статье, иллюстрацию экспериментального аппарата Ома.
- Щагрин, Мортон Л. (1963). «Сопротивление закону Ома». Американский журнал физики. 31 (7): 536–547. Bibcode:1963AmJPh..31..536S. Дои:10.1119/1.1969620. S2CID 120421759. Исследует концептуальные изменения, лежащие в основе экспериментальной работы Ома.
- Кеннет Л. Канева, «О, Георг Симон». Полный словарь научной биографии. 2008
- s: Scientific Memoirs / 2 / Математическое исследование гальванической цепи., перевод оригинальной статьи Ома.













































