Математическая морфология - Mathematical morphology

Математическая морфология (ММ) - теория и методика анализа и обработки геометрический конструкции, основанные на теория множеств, теория решетки, топология, и случайные функции. ММ чаще всего применяется к цифровые изображения, но его можно использовать и на графики, поверхностные сетки, твердые вещества, и многие другие пространственные конструкции.
Топологический и геометрический непрерывный -пространственные понятия, такие как размер, форма, выпуклость, возможность подключения, и геодезическое расстояние, были введены ММ как на непрерывной, так и на непрерывной дискретные пространства. ММ также является основой морфологического обработка изображений, который состоит из набора операторов, преобразующих изображения в соответствии с приведенными выше характеристиками.
Основные морфологические операторы: эрозия, расширение, открытие и закрытие.
ММ изначально разрабатывался для двоичные изображения, а позже был расширен до оттенки серого функции и изображения. Последующее обобщение на полные решетки сегодня широко используется в качестве теоретической основы ММ.
История
Еще с 1960-х годов всевозможные схемы нелинейной обработки изображений обсуждаются и используются в определенных сообществах. Примером, изначально популярным в науках о Земле и окружающей среде, является математическая морфология, основанная на «расширении» данных, состоящих из нулей и единиц, с «структурирующим элементом» σ в соответствии со знаком [ListConvolve [σ, data, 1, 0]] (как а так же двойная операция "эрозия").[1] Математическая морфология была разработана в 1964 году совместной работой Жорж Матерон и Жан Серра, на École des Mines de Paris, Франция. Матерон руководил кандидат наук Тезис Серры, посвященный количественной оценке минеральных характеристик из тонких поперечные сечения, и эта работа привела к новому практическому подходу, а также к теоретическим достижениям в интегральная геометрия и топология.
В 1968 г. Centre de Morphologie Mathématique была основана École des Mines de Paris в Фонтенбло Франция, во главе с Матероном и Серрой.
В течение оставшейся части 1960-х и большей части 1970-х годов ММ в основном занималась двоичные изображения, рассматриваемый как наборы, и сгенерировал большое количество бинарные операторы и техники: Преобразование попадания или промаха, расширение, эрозия, открытие, закрытие, гранулометрия, прореживание, скелетонизация, окончательная эрозия, условная биссектриса, и другие. Был также разработан случайный подход, основанный на новых моделях изображений. Большая часть произведений того периода была разработана в Фонтенбло.
С середины 1970-х до середины 1980-х годов ММ была обобщена на оттенки серого функции и изображений также. Помимо расширения основных понятий (таких как расширение, эрозия и т. Д.) На функции, это обобщение привело к появлению новых операторов, таких как морфологические градиенты, преобразование в цилиндр и Водораздел (Основная сегментация подход).
В 1980-х и 1990-х годах ММ получила более широкое признание, поскольку исследовательские центры в нескольких странах начали применять и исследовать этот метод. ММ начали применять для решения большого количества задач и приложений для обработки изображений.
В 1986 году Серра еще больше обобщил ММ, на этот раз до теоретической основы, основанной на полные решетки. Это обобщение внесло гибкость в теорию, сделав возможным ее применение к гораздо большему количеству структур, включая цветные изображения, видео и т. Д. графики, сетки и т. д. В то же время Матерон и Серра также сформулировали теорию морфологического фильтрация, основанный на новом решетчатом каркасе.
В 1990-е и 2000-е годы также произошел дальнейший теоретический прогресс, в том числе концепции связи и выравнивания.
В 1993 г. состоялся первый Международный симпозиум по математической морфологии (ISMM) в г. Барселона, Испания. С тех пор ISMM организуются каждые 2–3 года: Фонтенбло, Франция (1994); Атланта, Соединенные Штаты Америки (1996); Амстердам, Нидерланды (1998); Пало-Альто, CA, Соединенные Штаты Америки (2000); Сидней, Австралия (2002); Париж, Франция (2005); Рио де Жанейро, Бразилия (2007); Гронинген, Нидерланды (2009); Интра (Вербания ), Италия (2011); Упсала, Швеция (2013); Рейкьявик, Исландия (2015 г.); и Фонтенбло, Франция (2017).
Рекомендации
- «Вступление» Пьера Сойля в (Серра и другие. (Ред.) 1994 ), стр. 1-4.
- «Приложение A:« Центр морфологии математики », обзор» Жана Серра, в (Серра и другие. (Ред.) 1994 ), стр. 369-374.
- «Предисловие» в (Ронсе и другие. (Ред.) 2005 г. )
Бинарная морфология
В бинарной морфологии изображение рассматривается как подмножество из Евклидово пространство или целочисленная сетка , для некоторого измерения d.
Структурирующий элемент
Основная идея бинарной морфологии состоит в том, чтобы исследовать изображение с помощью простой, заранее заданной формы, делая выводы о том, как эта форма соответствует или не соответствует формам на изображении. Этот простой «зонд» называется структурирующий элемент, и сам по себе является двоичным изображением (то есть подмножеством пространства или сетки).
Вот несколько примеров широко используемых элементов структурирования (обозначенных B):
- Позволять ; B открытый диск радиуса рс центром в начале координат.
- Позволять ; B представляет собой квадрат 3 × 3, то есть B = {(−1, −1), (−1, 0), (−1, 1), (0, −1), (0, 0), (0, 1), (1, −1), (1, 0), (1, 1)}.
- Позволять ; B это "крест", данный B = {(−1, 0), (0, −1), (0, 0), (0, 1), (1, 0)}.
Основные операторы
Основные операции инвариантны относительно сдвига (инвариант перевода ) операторы, сильно связанные с Дополнение Минковского.
Позволять E быть евклидовым пространством или целочисленной сеткой, и А двоичное изображение в E.
Эрозия

В эрозия двоичного изображения А структурирующим элементом B определяется
куда Bz это перевод B по вектору z, т.е. , .
Когда структурирующий элемент B имеет центр (например, B диск или квадрат), и этот центр расположен в начале координат E, затем размывание А к B можно понимать как локус точек, достигнутых центром B когда B движется внутрь А. Например, эрозия квадрата со стороной 10 с центром в начале координат диском с радиусом 2, также центрированным в начале координат, представляет собой квадрат со стороной 6 с центром в начале координат.
Эрозия А к B также дается выражением .
Пример заявки: Предположим, мы получили факс с темной фотокопией. Все выглядит так, будто написано пером, которое кровоточит. Процесс эрозии позволит более толстым линиям стать тонкими и обнаружить дыру внутри буквы «о».
Расширение

В расширение из А структурирующим элементом B определяется
Расширение коммутативно, также задается .
Если B имеет центр в начале координат, как и раньше, то расширение А к B можно понимать как геометрическое место точек, покрытых B когда центр B движется внутрь А. В приведенном выше примере расширение квадрата стороны 10 диском радиуса 2 представляет собой квадрат стороны 14 с закругленными углами с центром в начале координат. Радиус скругленных углов - 2.
Расширение также можно получить с помощью , куда Bs обозначает симметричный из B, то есть, .
Пример применения: дилатация - это двойная операция эрозии. Фигуры, которые нарисованы очень слабо, становятся толстыми при «расширении». Самый простой способ описать это - представить, что тот же факс / текст написан более толстым пером.
Открытие

В открытие из А к B получается эрозией А к B, с последующим растяжением полученного изображения на B:
Открытие также дано , что означает, что это место переводов структурирующего элемента B внутри изображения А. В случае квадрата стороны 10 и диска с радиусом 2 в качестве структурирующего элемента проем представляет собой квадрат со стороной 10 со скругленными углами, где радиус угла равен 2.
Пример применения: предположим, что кто-то написал записку на не промокшей бумаге, и надпись выглядит так, как будто на ее поверхности растут крошечные волосатые корни. Открытие по существу устраняет внешние крошечные "волосяные утечки" и восстанавливает текст. Побочный эффект в том, что он завершает все. Острые края начинают исчезать.
Закрытие
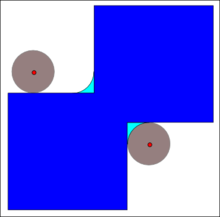
В закрытие из А к B получается расширением А к Bс последующим размывом получившейся структуры на B:
Закрытие также может быть получено , куда Иксc обозначает дополнять из Икс относительно E (то есть, ). Вышесказанное означает, что закрытие является дополнением локуса переводов симметричного структурирующего элемента за пределы изображения. А.
Свойства основных операторов
Вот некоторые свойства основных бинарных морфологических операторов (расширение, эрозия, открытие и закрытие):
- Они есть инвариант перевода.
- Они есть увеличение, то есть если , тогда , и , так далее.
- Расширение коммутативный: .
- Если происхождение E принадлежит к элементу структурирования B, тогда .
- Расширение ассоциативный, т.е. . Кроме того, эрозия удовлетворяет .
- Эрозия и расширение удовлетворяют двойственность .
- Открытие и закрытие удовлетворяют двойственность .
- Расширение распределительный над установить союз
- Эрозия распределительный над установить пересечение
- Расширение - это псевдообратный эрозии, и наоборот, в следующем смысле: если и только если .
- Открытие и закрытие идемпотент.
- Открытие антиэкстенсивный, т.е. , а закрытие обширный, т.е. .
Другие операторы и инструменты
- Преобразование попадания или промаха
- Преобразование обрезки
- Морфологический скелет
- Фильтрация по реконструкции
- Окончательные эрозии и условные биссектрисы
- Гранулометрия
- Функции геодезического расстояния
Морфология оттенков серого

В оттенки серого морфология, изображения функции отображение Евклидово пространство или сетка E в , куда это набор реалы, является элементом больше любого действительного числа, и это элемент меньше любого действительного числа.
Структурирующие элементы шкалы серого также являются функциями того же формата, называемыми «функциями структурирования».
Обозначение изображения ж(Икс) и структурирующей функцией б(Икс), расширение оттенков серого ж к б дан кем-то
где "sup" обозначает супремум.
Точно так же эрозия ж к б дан кем-то
где "inf" обозначает инфимум.
Как и в бинарной морфологии, открытие и закрытие задаются соответственно
Функции плоского структурирования
Плоские структурирующие элементы часто используются в морфологических приложениях. Функции плоского структурирования - это функции б(Икс) в виде
куда .
В этом случае расширение и эрозия значительно упрощены и соответственно задаются
В ограниченном дискретном случае (E это сетка и B ограничен), супремум и инфимум операторы можно заменить на максимум и минимум. Таким образом, расширение и эрозия являются частными случаями статистика заказов фильтры, с расширением, возвращающим максимальное значение в пределах движущегося окна (симметричный элемент поддержки функции структурирования B), а эрозия возвращает минимальное значение в движущемся окне B.
В случае плоского структурирующего элемента морфологические операторы зависят только от относительного упорядочения пиксель значения, независимо от их числовых значений, и поэтому особенно подходят для обработки двоичные изображения и изображения в оттенках серого чей световая передаточная функция не известно.
Другие операторы и инструменты
Комбинируя эти операторы, можно получить алгоритмы для многих задач обработки изображений, таких как обнаружение функции, сегментация изображения, резкость изображения, фильтрация изображений, и классификация. Вдоль этой строки следует также обратить внимание на Непрерывная морфология [2]
Математическая морфология на полных решетках
Полные решетки находятся частично упорядоченные наборы, где каждое подмножество имеет инфимум и супремум. В частности, он содержит наименьший элемент и величайший элемент (также обозначается «вселенная»).
Приросты (расширение и эрозия)
Позволять - полная решетка, нижняя и верхняя грань которой символизируются и , соответственно. Его вселенная и наименьший элемент символизируются U и , соответственно. Кроме того, пусть быть набором элементов из L.
Расширение - это любой оператор который распределяется по супремуму и сохраняет наименьший элемент. То есть:
- ,
- .
Эрозия - это любой оператор который распределяет по инфимуму и сохраняет вселенную. То есть:
- ,
- .
Форма дилатаций и эрозий Связи Галуа. То есть для каждого расширения есть одна и только одна эрозия это удовлетворяет
для всех .
Точно так же для каждой эрозии есть одно и только одно расширение, удовлетворяющее вышеуказанной связи.
Кроме того, если два оператора удовлетворяют соединению, то должно быть расширение, и эрозия.
Пары эрозий и дилатаций, удовлетворяющие вышеуказанной связи, называются «присоединениями», а эрозия называется сопутствующей эрозией расширения и наоборот.
Открытие и закрытие
Для каждого примыкания , морфологическое отверстие и морфологическое закрытие определяются следующим образом:
Морфологическое открытие и закрытие - частные случаи алгебраическое открытие (или просто открытие) и алгебраическое замыкание (или просто закрытие). Алгебраические открытия - это операторы в L которые являются идемпотентными, увеличивающимися и антиэкстенсивными. Алгебраические замыкания - это операторы в L которые являются идемпотентными, растущими и обширными.
Частные случаи
Бинарная морфология - это частный случай морфологии решетки, где L это набор мощности из E (Евклидово пространство или сетка), то есть L - это множество всех подмножеств E, и это установить включение. В этом случае нижняя грань равна установить пересечение, а супремум установить союз.
Точно так же морфология оттенков серого - это еще один частный случай, когда L набор функций отображения E в , и , , и , - точечный порядок, супремум и инфимум соответственно. То есть ж и грамм функции в L, тогда если и только если ; инфимум дан кем-то ; и супремум дан кем-то .
Смотрите также
Примечания
- ^ Вольфрам, Стивен (2002). Новый вид науки. Wolfram Media, Inc. стр.1077. ISBN 1-57955-008-8.
- ^ Г. Сапиро, Р. Киммел, Д. Шакед, Б. Кимиа и А. М. Брукштейн. Реализация морфологии непрерывного масштаба через эволюцию кривой. Распознавание образов, 26 (9): 1363–1372, 1993.
Рекомендации
- Анализ изображений и математическая морфология Жан Серра, ISBN 0-12-637240-3 (1982)
- Анализ изображений и математическая морфология, Том 2: Теоретические достижения Жан Серра, ISBN 0-12-637241-1 (1988)
- Введение в морфологическую обработку изображений Эдвард Р. Догерти, ISBN 0-8194-0845-X (1992)
- Морфологический анализ изображений; Принципы и применение Пьер Сойль, ISBN 3-540-65671-5 (1999), 2-е издание (2003)
- Математическая морфология и ее применение к обработке сигналов, J. Serra и Ph. Salembier (Eds.), Материалы 1-го Международного семинара по математической морфологии и ее приложениям к обработке сигналов (ISMM'93), ISBN 84-7653-271-7 (1993)
- Математическая морфология и ее приложения к обработке изображений, J. Serra и P. Soille (Eds.), Труды 2-го международного симпозиума по математической морфологии (ISMM'94), ISBN 0-7923-3093-5 (1994)
- Математическая морфология и ее приложения к обработке изображений и сигналов, Хенк Дж.А.М. Хейманс и Джос Б.Т.М. Рёрдинка (ред.), Труды 4-го международного симпозиума по математической морфологии (ISMM'98), ISBN 0-7923-5133-9 (1998)
- Математическая морфология: 40 лет спустя, Кристиан Ронс, Лоран Наджман и Этьен Десенсьер (ред.), ISBN 1-4020-3442-3 (2005)
- Математическая морфология и ее приложения к обработке сигналов и изображений, Джеральд Дж. Ф. Банон, Джуниор Баррера, Улисс М. Брага-Нето (ред.), Материалы 8-го международного симпозиума по математической морфологии (ISMM'07), ISBN 978-85-17-00032-4 (2007)
- Математическая морфология: от теории к приложениям, Лоран Наджман и Хьюг Талбот (редакторы). ISTE-Wiley. ISBN 978-1-84821-215-2. (520 стр.) Июнь 2010 г.
внешняя ссылка
- Онлайн-курс по математической морфологии, Жан Серра (на английском, французском и испанском языках)
- Центр математической морфологии, Парижская горная школа
- История математической морфологии, Жорж Матерон и Жан Серра
- Morphology Digest, информационный бюллетень по математической морфологии, Пьер Сойль
- Лекции по обработке изображений: сборник из 18 лекций в формате pdf из Университета Вандербильта. Лекции 16-18 посвящены математической морфологии., Алан Питерс
- Математическая морфология; из лекций по компьютерному зрению, к Робин Оуэнс
- Бесплатная оптимизированная библиотека обработки изображений SIMD
- Демонстрация Java-апплета
- ФИЛЬТРЫ: бесплатная библиотека обработки изображений с открытым исходным кодом
- Быстрые морфологические эрозии, расширения, открытия и закрытия
- Морфологический анализ нейронов с помощью Matlab


































![{ Displaystyle (е oplus b) (х) = sup _ {y in E} [f (y) + b (x-y)],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bf4139e186aeaf17e8dd6e8c2ce2d23e232b70bd)
![{ Displaystyle (е ominus b) (х) = inf _ {y in E} [f (y) -b (y-x)],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8eebd4eabeaa7c5e9552b3cff472c6b7ee4ea613)
































