Линза - Lens

Для использования в других целях см. Линза (значения).

Двояковыпуклая линза

Линзы можно использовать для фокусировки света

А линза является трансмиссивным оптический устройство, которое фокусирует или рассеивает луч света посредством преломление. А простой объектив состоит из одного куска прозрачный материал, а составная линза состоит из нескольких простых линз (элементы), обычно располагаются вдоль общей ось. Линзы изготавливаются из таких материалов, как стекло или же пластик, и являются земля и полированный или же формованный до желаемой формы. Линза может фокусировать свет, чтобы сформировать изображение в отличие от призма, который преломляет свет без фокусировки. Устройства, которые аналогичным образом фокусируют или рассеивают волны и излучение, отличное от видимого света, также называются линзами, например микроволновая печь линзы, электронные линзы, акустические линзы или взрывные линзы.

История

Смотрите также: История оптики и Объектив

Свет преломляется сферическим стеклянным сосудом, наполненным водой. Роджер Бэкон, 13 век

Объектив для LSST, планируемый небесный телескоп

Слово линза происходит от Lēns, латинское название чечевица, потому что двояковыпуклая линза имеет форму чечевицы. Чечевица также дает название геометрическая фигура.^[1]

Некоторые ученые утверждают, что археологические свидетельства указывают на широкое использование линз в древности, охватывающее несколько тысячелетий.^[2] Так называемой Линза Нимруда - артефакт из горного хрусталя, датируемый 7 веком до нашей эры, который мог использоваться или не использоваться в качестве увеличительного стекла или горящего стекла.^[3][4][5] Другие предположили, что некоторые Египетские иероглифы изображают «простые стеклянные менисковые линзы».^{[6][требуется проверка ]}

Самая старая достоверная ссылка на использование линз взята из Аристофан ' играть в Облака (424 г. до н.э.) упоминание горящего стекла.^[7]Плиний Старший (1 век) подтверждает, что горящие стаканы были известны еще в римский период.^[8]Плиний также имеет самое раннее известное упоминание об использовании корректирующая линза когда он упоминает это Неро было сказано смотреть гладиаторский игры с использованием изумруд (предположительно вогнутый поправить близорукость, правда ссылка расплывчата).^[9] И Плиний, и Сенека Младший (3 г. до н.э. – 65 г. н.э.) описал увеличивающий эффект стеклянного шара, наполненного водой.

Птолемей (2 век) написал книгу о Оптика, который, однако, сохранился только в латинском переводе неполного и очень плохого арабского перевода. Книга была, однако, принята средневековыми учеными в исламском мире и прокомментирована Ибн Сахл (10 век), который, в свою очередь, был улучшен Альхазен (Книга оптики, 11 век). Арабский перевод книги Птолемея Оптика стал доступен в латинском переводе в XII веке (Евгений Палермский 1154). Между 11 и 13 веками "камни для чтения "были изобретены. Это были примитивные плоско-выпуклые линзы, первоначально сделанные путем разрезания стеклянной сферы пополам. Средневековый (11 или 12 век) горный хрусталь Линзы Visby могли или не могли быть предназначены для использования в качестве горящих очков.^[10]

Очки были изобретены как усовершенствование «камней для чтения» периода высокого средневековья в Северной Италии во второй половине 13 века.^[11] Это было началом оптической индустрии шлифовки и полировки линз для очков, впервые в Венеции и Флоренции в конце 13 века.^[12] а затем и в зрелищных центрах как в Нидерланды и Германия.^[13]Создатели очков создали улучшенные типы линз для коррекции зрения, основанные больше на эмпирических знаниях, полученных при наблюдении за эффектами линз (вероятно, без знания элементарной оптической теории того времени).^[14][15] Практические разработки и эксперименты с линзами привели к изобретению соединения. оптический микроскоп около 1595 г., а рефракторный телескоп в 1608 году, оба из них появились в зрелищных центрах в Нидерланды.^[16][17]

Дальнейшая информация: История телескопа

С изобретением телескопа и микроскопа в 17 и начале 18 веков было проведено множество экспериментов с формами линз теми, кто пытался исправить хроматические ошибки, наблюдаемые в линзах. Оптики пытались конструировать линзы различной формы кривизны, ошибочно полагая, что ошибки возникли из-за дефектов сферической формы их поверхностей.^[18] Оптическая теория на преломление и эксперименты показали, что ни один одноэлементный объектив не может сфокусировать все цвета. Это привело к изобретению соединения ахроматическая линза к Честер Мур Холл в Англия в 1733 году на изобретение также претендовал соотечественник-англичанин. Джон Доллонд в патенте 1758 г.

Построение простых линз

Большинство линз сферические линзы: их две поверхности являются частями поверхностей сфер. Каждая поверхность может быть выпуклый (выпирая наружу из линзы), вогнутый (вдавлен в линзу), или планарный (плоский). Линия, соединяющая центры сфер, составляющих поверхности линз, называется ось линзы. Обычно ось линзы проходит через физический центр линзы из-за способа их изготовления. После изготовления линзы можно разрезать или отшлифовать, чтобы придать им другую форму или размер. В этом случае ось линзы может не проходить через физический центр линзы.

Торический или сферо-цилиндрические линзы имеют поверхности с двумя разными радиусами кривизны в двух ортогональных плоскостях. У них разные фокусная сила в разных меридианах. Это формирует астигматизм линза. Примером могут служить линзы для очков, которые используются для коррекции астигматизм в чьих-то глазах.

Типы простых линз

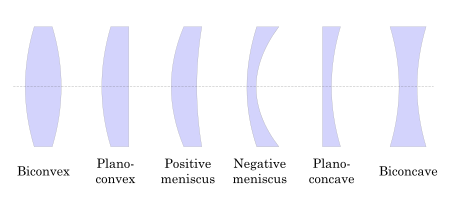
Линзы классифицируются по кривизне двух оптических поверхностей. Объектив двояковыпуклый (или же двояковыпуклый, или просто выпуклый), если обе поверхности выпуклый. Если обе поверхности имеют одинаковый радиус кривизны, линза равновыпуклый. Объектив с двумя вогнутый поверхности двояковыпуклый (или просто вогнутый). Если одна из поверхностей плоская, линза плосковыпуклый или же плосковогнутый в зависимости от кривизны другой поверхности. Линза с одной выпуклой и одной вогнутой стороной выпукло-вогнутый или же мениск. Именно этот тип линз чаще всего используется в корректирующие линзы.

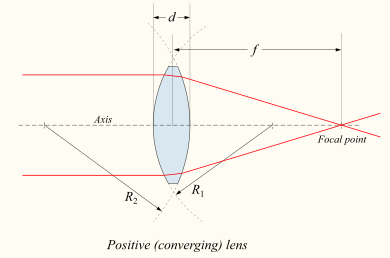
Если хрусталик двояковыпуклый или плосковыпуклый, коллимированный луч света, проходящий через линзу, сходится к точке ( фокус) за линзой. В этом случае линза называется положительный или же сходящийся линза. Для тонкая линза в воздухе расстояние от линзы до пятна равно фокусное расстояние линзы, которая обычно представлена ж в диаграммах и уравнениях. An удлиненная полусферическая линза - это особый тип плоско-выпуклой линзы, в которой криволинейная поверхность линзы представляет собой полную полусферу, а толщина линзы намного превышает радиус кривизны.

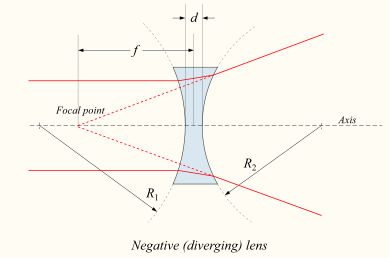
Если линза двояковогнутая или плосковогнутая, коллимированный пучок света, проходящий через линзу, расходится (рассеивается); линза, таким образом, называется отрицательный или же расходящиеся линза. Луч, прошедший через линзу, кажется, исходит из определенной точки на оси перед линзой. Для тонкой линзы в воздухе расстояние от этой точки до линзы является фокусным расстоянием, хотя оно отрицательно по сравнению с фокусным расстоянием собирающей линзы.

Выпукло-вогнутые (менисковые) линзы могут быть как положительными, так и отрицательными, в зависимости от относительной кривизны двух поверхностей. А отрицательный мениск Линза имеет более крутую вогнутую поверхность и тоньше в центре, чем на периферии. И наоборот, a положительный мениск Линза имеет более крутую выпуклую поверхность и толще в центре, чем на периферии. Идеальный тонкая линза с двумя поверхностями одинаковой кривизны имел бы ноль оптическая сила, что означает, что он не будет ни сходиться, ни рассеивать свет. Однако все настоящие линзы имеют ненулевую толщину, что делает реальную линзу с идентичными изогнутыми поверхностями слегка положительной. Чтобы получить точно нулевую оптическую силу, менисковая линза должна иметь слегка неодинаковую кривизну, чтобы учесть влияние толщины линзы.

Уравнение линзмейкера

Фокусное расстояние объектива в воздухе можно рассчитать из уравнение производителя линз:^[19]

${displaystyle {frac {1}{f}}=(n-1)left[{frac {1}{R_{1}}}-{frac {1}{R_{2}}}+{frac {(n-1)d}{nR_{1}R_{2}}}ight],}$

куда

${displaystyle f}$ фокусное расстояние объектива,

${displaystyle n}$ это показатель преломления материала линзы,

${displaystyle R_{1}}$ это радиус кривизны (со знаком, см. ниже) поверхности линзы ближе к источнику света,

${displaystyle R_{2}}$ - радиус кривизны поверхности линзы дальше от источника света, а

${displaystyle d}$ - толщина линзы (расстояние по оси линзы между двумя вершины поверхности ).

Фокусное расстояние ж является положительным для собирающих линз и отрицательным для расходящихся линз. В взаимный фокусного расстояния, 1 /ж, это оптическая сила линзы. Если фокусное расстояние указано в метрах, это дает оптическую силу в диоптрии (обратные метры).

У линз такое же фокусное расстояние, когда свет движется от задней части к передней, как и когда свет идет от передней части к задней. Другие свойства линзы, такие как аберрации не одинаковы в обоих направлениях.

Соглашение о знаках радиусов кривизны р₁ и р₂

Основная статья: Радиус закругления (оптика)

Знаки радиусов кривизны линзы указывают, являются ли соответствующие поверхности выпуклыми или вогнутыми. В подписать соглашение используется для обозначения этого по-разному, но в этой статье положительный р указывает, что центр кривизны поверхности находится дальше по направлению движения луча (справа на прилагаемых диаграммах), а отрицательный р означает, что лучи, достигающие поверхности, уже прошли центр кривизны. Следовательно, для внешних поверхностей линз, как показано выше, р₁ > 0 и р₂ < 0 указывать выпуклый поверхности (используются для сведения света в положительной линзе), а р₁ < 0 и р₂ > 0 указывать вогнутый поверхности. Величина, обратная радиусу кривизны, называется кривизна. Плоская поверхность имеет нулевую кривизну, а ее радиус кривизны равен бесконечность.

Приближение тонкой линзы

Если d маленький по сравнению с р₁ и р₂, то тонкая линза приближение может быть сделано. Для линзы в воздухе, ж тогда дается

${displaystyle {frac {1}{f}}approx left(n-1ight)left[{frac {1}{R_{1}}}-{frac {1}{R_{2}}}ight].}$^[20]

Свойства изображения

Как упоминалось выше, положительная или собирающая линза в воздухе фокусирует коллимированный луч, движущийся вдоль оси линзы, в точку (известную как координационный центр ) На расстоянии ж от объектива. И наоборот, a точечный источник света, помещенного в точку фокусировки, линза преобразует в коллимированный луч. Эти два случая являются примерами изображение образование в линзах. В первом случае объект на бесконечном расстоянии (представленный коллимированным пучком волн) фокусируется на изображение в фокусной точке линзы. В последнем случае объект на фокусном расстоянии от объектива отображается на бесконечности. Плоскость, перпендикулярная оси линзы, расположенная на расстоянии ж от объектива называется фокальная плоскость.

Если расстояния от объекта до объектива и от объектива до изображения равны S₁ и S₂ соответственно для линзы пренебрежимо малой толщины (тонкая линза ) в воздухе расстояния связаны соотношением формула тонкой линзы:^[21][22][23]

${displaystyle {frac {1}{S_{1}}}+{frac {1}{S_{2}}}={frac {1}{f}}.}$

Это также можно представить в «ньютоновской» форме:

${displaystyle x_{1}x_{2}=f^{2},!}$^[24]

куда ${displaystyle x_{1}=S_{1}-f}$ и ${displaystyle x_{2}=S_{2}-f}$.

Объектив камеры образует реальное изображение удаленного объекта.

Следовательно, если объект находится на расстоянии S₁ > ж от положительной линзы фокусного расстояния ж, найдем расстояние изображения S₂ по этой формуле. Если экран расположен на расстоянии S₂ на противоположной стороне линзы на ней формируется изображение. Это своего рода изображение, которое можно проецировать на экран или датчик изображений, известен как реальное изображение. Кроме того, это реальное изображение также можно просмотреть человеческие глаза, как показано на рисунке ниже (с подписью «Выпуклая линза (ж ≪ S₁) образуя реальный перевернутый образ ... »).

Формирование виртуального изображения с помощью положительной линзы в качестве увеличительного стекла.^[25]

Это принцип камера, и из человеческий глаз. Регулировка фокусировки камеры регулирует S₂, поскольку использование расстояния изображения, отличного от требуемого этой формулой, дает расфокусированный (нечеткое) изображение объекта на расстоянии S₁ с камеры. Другими словами, изменение S₂ вызывает объекты в разных S₁ прийти в идеальный фокус.

В некоторых случаях S₂ имеет отрицательное значение, указывая на то, что изображение формируется на противоположной стороне линзы, от которой учитываются эти лучи. Поскольку расходящиеся световые лучи, исходящие из линзы, никогда не попадают в фокус, и эти лучи физически не присутствуют в той точке, где они появляться для формирования изображения это называется виртуальное изображение. В отличие от реальных изображений, виртуальное изображение не может быть спроецировано на экран, оно кажется наблюдателю, смотрящему через линзу, как если бы оно было реальным объектом в месте расположения этого виртуального изображения. Точно так же последующему объективу кажется, что это объект в этом месте, так что второй объектив может снова сфокусировать этот свет на реальное изображение, S₁ затем измеряется от местоположения виртуального изображения за первой линзой до второй линзы. Именно это и делает глаз, смотрящий сквозь увеличительное стекло. Увеличительное стекло создает (увеличенное) виртуальное изображение за увеличительным стеклом, но затем эти лучи воспроизводятся повторно. хрусталик глаза создать реальное изображение на сетчатка.

А отрицательный линза производит уменьшенное виртуальное изображение.

А Линза Барлоу (B) перерисовывает a виртуальный объект (фокус пути красного луча) в увеличенное реальное изображение (зеленые лучи в фокусе)

Использование линзы с положительным фокусным расстоянием ж, виртуальное изображение получается, когда S₁ < ж, таким образом, линза используется как увеличительное стекло (а не S₁ >> ж как по фотоаппарату). Использование отрицательной линзы (ж < 0) с реальный объект (S₁ > 0) может создавать только виртуальное изображение (S₂ < 0) согласно приведенной выше формуле. Также возможно расстояние до объекта S₁ быть отрицательным, и в этом случае линза видит так называемый виртуальный объект. Это происходит, когда линза вставляется в сходящийся луч (фокусируется предыдущей линзой). перед местонахождение его реального изображения. В этом случае даже негативная линза может проецировать реальное изображение, как это делает Линза Барлоу.

На экран проецируется реальное изображение лампы (перевернутое). Видны отражения лампы от обеих поверхностей двояковыпуклой линзы.

Выпуклая линза (ж ≪ S₁), формируя реальное перевернутое изображение (как изображение, сформированное линзой объектива телескопа или бинокля), а не вертикальное виртуальное изображение, как на увеличительное стекло (ж > S₁). Этот реальное изображение также можно просмотреть, если положить на экран.

Для тонкая линза, расстояния S₁ и S₂ измеряются от объекта и изображения до положения линзы, как описано выше. Когда толщина линзы не намного меньше S₁ и S₂ или имеется несколько элементов объектива ( составная линза ), вместо этого нужно измерять расстояние от объекта и изображения до основные самолеты линзы. Если расстояния S₁ или же S₂ пройти через средний кроме воздуха или вакуума требуется более сложный анализ.

Увеличение

Линейный увеличение системы визуализации с использованием одной линзы определяется выражением

${displaystyle M=-{frac {S_{2}}{S_{1}}}={frac {f}{f-S_{1}}},}$

куда M - коэффициент увеличения, определяемый как отношение размера изображения к размеру объекта. Знаковое соглашение здесь гласит, что если M отрицательно, как и для реальных изображений, изображение перевернуто по отношению к объекту. Для виртуальных образов M положительный, значит изображение вертикальное.

Эта формула увеличения предоставляет два простых способа отличить сходящиеся (f> 0) и расходящиеся (f <0) линзы: для объекта, очень близкого к линзе (0 < S₁ <| f |), собирающая линза будет формировать увеличенное (большее) виртуальное изображение, тогда как расходящаяся линза будет формировать уменьшенное (меньшее) изображение; Для объекта, находящегося очень далеко от объектива (S₁ > | f | > 0), собирающая линза будет формировать перевернутое изображение, тогда как расходящаяся линза будет формировать прямое изображение.

Линейное увеличение M не всегда является самым полезным показателем увеличительной силы. Например, при описании визуального телескопа или бинокля, которые производят только виртуальное изображение, больше внимания будет уделяться угловое увеличение - что выражает, насколько более далекий объект кажется через телескоп по сравнению с невооруженным глазом. В случае камеры можно процитировать пластинчатая шкала, который сравнивает видимый (угловой) размер удаленного объекта с размером реального изображения, полученного в фокусе. Шкала пластинки обратно пропорциональна фокусному расстоянию объектива камеры; линзы относятся к категории длиннофокусные линзы или же широкоугольные объективы согласно их фокусным расстояниям.

Использование неподходящего измерения увеличения может быть формально правильным, но дать бессмысленное число. Например, при использовании увеличительного стекла с фокусным расстоянием 5 см, расположенного на расстоянии 20 см от глаза и 5 см от объекта, создается виртуальное изображение бесконечного линейного размера на бесконечности: M = ∞. Но угловое увеличение равно 5, что означает, что объект кажется глазу в 5 раз больше, чем без линзы. При фотографировании Луна используя камеру с объективом 50 мм, линейное увеличение не заботит M ≈ −50 мм / 380000 км = −1.3×10⁻¹⁰. Скорее, масштаб пластины камеры составляет около 1 ° / мм, из чего можно сделать вывод, что изображение 0,5 мм на пленке соответствует угловому размеру Луны, наблюдаемому с Земли, примерно 0,5 °.

В крайнем случае, когда объект находится на бесконечном расстоянии, S₁ = ∞, S₂ = ж и M = −ж/∞= 0, что указывает на то, что объект будет отображаться в единственной точке фокальной плоскости. На самом деле диаметр проецируемого пятна на самом деле не равен нулю, поскольку дифракция устанавливает нижний предел размера функция разброса точки. Это называется предел дифракции.

Изображения черных букв в тонкой выпуклой линзе фокусного расстояния ж показаны красным. Выбранные лучи показаны для букв E, я и K синим, зеленым и оранжевым цветом соответственно. Обратите внимание, что E (в 2ж) имеет реальное и перевернутое изображение равного размера; я (в ж) имеет свой образ в бесконечность; и K (в ж/ 2) имеет двойное виртуальное вертикальное изображение.

Аберрации

Оптическая аберрация
Расфокусировать Наклон Сферическая аберрация Астигматизм Кома Искажение Кривизна поля Пецваля Хроматическая аберрация

Основная статья: Оптическая аберрация

Линзы не формируют идеальное изображение, а объектив всегда вносит некоторую степень искажения или искажения. аберрация что делает изображение несовершенной копией объекта. Тщательная конструкция системы линз для конкретного применения сводит к минимуму аберрации. На качество изображения влияют несколько типов аберраций, включая сферическую аберрацию, кому и хроматическую аберрацию.

Сферическая аберрация

Основная статья: Сферическая аберрация

Сферическая аберрация возникает из-за того, что сферические поверхности не являются идеальной формой для линз, но, безусловно, являются самой простой формой, в которой стекло может быть шлифованный и полированный, и поэтому часто используются. Сферическая аберрация приводит к тому, что лучи, параллельные оси линзы, но удаленные от нее, фокусируются в несколько ином месте, чем лучи, расположенные близко к оси. Это проявляется в размытии изображения. Сферическую аберрацию можно свести к минимуму с помощью линз нормальной формы, тщательно выбирая кривизну поверхности для конкретного применения. Например, плоско-выпуклая линза, которая используется для фокусировки коллимированного луча, создает более резкое фокусное пятно, когда используется выпуклой стороной по направлению к источнику луча.

Кома

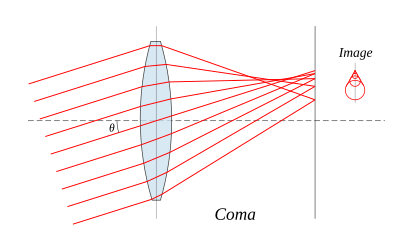
Основная статья: Кома (оптика)

Кома, или же коматическая аберрация, получил свое название от комета -подобный вид аберрированного изображения. Кома возникает, когда объект отображается за пределами оптической оси линзы, когда лучи проходят через линзу под углом к ​​оси θ. Лучи, проходящие через центр линзы с фокусным расстоянием ж сфокусированы в точке на расстоянии ж загар θ от оси. Лучи, проходящие через внешние края линзы, фокусируются в разных точках, либо дальше от оси (положительная кома), либо ближе к оси (отрицательная кома). Как правило, пучок параллельных лучей, проходящих через линзу на фиксированном расстоянии от центра линзы, фокусируется на изображение в форме кольца в фокальной плоскости, известное как коматический круг. Сумма всех этих кругов дает V-образную или кометоподобную вспышку. Как и в случае со сферической аберрацией, кома может быть минимизирована (а в некоторых случаях устранена) путем выбора кривизны двух поверхностей линз в соответствии с приложением. Линзы, в которых минимизированы как сферическая аберрация, так и кома, называются лучшая форма линзы.

Хроматическая аберрация

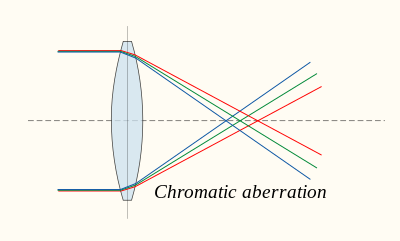
Основная статья: Хроматическая аберрация

Хроматическая аберрация вызвано разброс материала линзы - вариация ее показатель преломления, п, с длиной волны света. Поскольку из приведенных выше формул ж зависит от п, следовательно, свет с разной длиной волны фокусируется в разные позиции. Хроматическая аберрация объектива видна как цветные полосы вокруг изображения. Его можно минимизировать, используя ахроматический дублет (или же ахромат), в котором два материала с разной дисперсией связаны вместе, образуя единую линзу. Это уменьшает количество хроматических аберраций в определенном диапазоне длин волн, хотя и не дает идеальной коррекции. Использование ахроматов было важным шагом в развитии оптического микроскопа. An апохромат - это линза или система линз с еще более совершенной коррекцией хроматической аберрации в сочетании с улучшенной коррекцией сферической аберрации. Апохроматы намного дороже ахроматов.

Для минимизации хроматической аберрации также могут использоваться различные материалы линз, такие как специальные покрытия или линзы, сделанные из кристалла. флюорит. Это природное вещество имеет самый высокий из известных Число Аббе, что указывает на низкую дисперсность материала.

Другие виды аберрации

Другие виды аберраций включают: кривизна поля, бочка и подушкообразное искажение, и астигматизм.

Апертурная дифракция

Даже если объектив сконструирован так, чтобы минимизировать или устранить аберрации, описанные выше, качество изображения все равно ограничено дифракция света, проходящего через линзу, конечная отверстие. А дифракционно ограниченный Линза - это линза, в которой аберрации уменьшены до такой степени, что качество изображения в основном ограничивается дифракцией в проектных условиях.

Составные линзы

Смотрите также: Фотографический объектив, Дублет (линза), Триплетная линза, и Ахроматическая линза

Простые линзы подлежат оптические аберрации обсуждалось выше. Во многих случаях эти аберрации можно в значительной степени компенсировать, используя комбинацию простых линз с дополнительными аберрациями. А составная линза представляет собой набор простых линз разной формы, изготовленных из материалов с разными показателями преломления, расположенных одна за другой с общей осью.

Самый простой случай - контакт линз: если линзы фокусных расстояний ж₁ и ж₂ находятся "тонкий ", комбинированное фокусное расстояние ж линз дается

${displaystyle {frac {1}{f}}={frac {1}{f_{1}}}+{frac {1}{f_{2}}}.}$

Поскольку 1 /ж это сила линзы, видно, что силы тонких линз в контакте складываются.

Если две тонкие линзы разделены в воздухе на некоторое расстояние d, фокусное расстояние для комбинированной системы равно

${displaystyle {frac {1}{f}}={frac {1}{f_{1}}}+{frac {1}{f_{2}}}-{frac {d}{f_{1}f_{2}}}.}$

Расстояние от передней точки фокусировки объектива до первой линзы называется переднее фокусное расстояние (FFL):

${displaystyle { ext{FFL}}={frac {f_{1}(f_{2}-d)}{(f_{1}+f_{2})-d}}.}$^[26]

Точно так же расстояние от второй линзы до задней фокусной точки комбинированной системы равно заднее фокусное расстояние (BFL):

${displaystyle { ext{BFL}}={frac {f_{2}(d-f_{1})}{d-(f_{1}+f_{2})}}.}$

В качестве d стремится к нулю, фокусные расстояния стремятся к значению ж дается для контактных тонких линз.

Если разделительное расстояние равно сумме фокусных расстояний (d = ж₁ + ж₂), FFL и BFL бесконечны. Это соответствует паре линз, которые преобразуют параллельный (коллимированный) пучок в другой коллимированный пучок. Такой тип системы называется афокальная система, так как это не приводит к чистому схождению или расхождению луча. Две линзы на таком расстоянии образуют простейший тип оптический телескоп. Хотя система не изменяет расходимость коллимированного луча, она изменяет ширину луча. Увеличение такого телескопа равно

${displaystyle M=-{frac {f_{2}}{f_{1}}},}$

который представляет собой отношение ширины выходного луча к ширине входного луча. Обратите внимание на условные обозначения: телескоп с двумя выпуклыми линзами (ж₁ > 0, ж₂ > 0) дает отрицательное увеличение, указывая на перевернутое изображение. Выпуклая плюс вогнутая линза (ж₁ > 0 > ж₂) обеспечивает положительное увеличение и изображение становится вертикальным. Для получения дополнительной информации о простых оптических телескопах см. Рефракционный телескоп § Конструкции рефракционных телескопов.

Несферические типы

Асферическая двояковыпуклая линза.

Цилиндрические линзы имеют кривизну только по одной оси. Они используются для фокусировки света в линию или для преобразования эллиптического света из лазерный диод в круглую балку. Они также используются в кино. анаморфные линзы.

Асферические линзы иметь по крайней мере одну поверхность, которая не является ни сферической, ни цилиндрической. Более сложные формы позволяют таким линзам формировать изображения с меньшими затратами. аберрация чем стандартные простые линзы, но их производство сложнее и дороже. Раньше их было сложно производить и часто было очень дорого, но технологический прогресс значительно снизил стоимость производства таких линз.

Крупный план квартиры Линза Френеля.

А Линза Френеля его оптическая поверхность разбита на узкие кольца, что позволяет линзам быть намного тоньше и легче обычных линз. Прочные линзы Френеля можно отливать из пластика и стоят недорого.

Линзовидные линзы массивы микролинзы которые используются в лентикулярная печать для создания изображений, которые имеют иллюзию глубины или которые меняются при просмотре под разными углами.

Бифокальная линза имеет два или более или градуированных фокусных расстояния, заточенных в объектив.

А линза с градиентным индексом имеет плоские оптические поверхности, но имеет радиальное или осевое изменение показателя преломления, которое заставляет свет, проходящий через линзу, фокусироваться.

An аксикон имеет конический оптическая поверхность. Он изображает точечный источник в линию вдоль то оптическая ось, или преобразует лазерный луч в кольцо.^[27]

Дифракционные оптические элементы могут работать как линзы.

Суперлинзы сделаны из метаматериалы с отрицательным индексом и утверждают, что производят изображения с пространственным разрешением, превышающим предел дифракции.^[28] Первые суперлинзы были сделаны в 2004 г. на такой метаматериал для микроволн.^[28] Улучшенные версии были сделаны другими исследователями.^[29][30] По состоянию на 2014 г.^{[Обновить]} суперлинза еще не была продемонстрирована на видимый или почти-инфракрасный длины волн.^[31]

Разработан прототип плоской сверхтонкой линзы без кривизны.^[32]

Использует

Одиночная выпуклая линза, установленная в оправе с ручкой или стойкой, представляет собой увеличительное стекло.

Линзы используются как протезирование для исправления аномалии рефракции Такие как миопия, гиперметропия, пресбиопия, и астигматизм. (Видеть корректирующая линза, контактные линзы, очки.) Большинство линз, используемых для других целей, имеют строгие осевая симметрия; линзы очков только приблизительно симметричны. Обычно они имеют форму примерно овальной, а не круглой рамки; оптические центры расположены над глазные яблоки; их кривизна не может быть осесимметричной, чтобы исправить астигматизм. Линзы солнцезащитных очков предназначены для ослабления света; Линзы для солнцезащитных очков, которые также корректируют нарушения зрения, могут быть изготовлены на заказ.

Другое использование - в системах обработки изображений, таких как монокуляры, бинокль, телескопы, микроскопы, камеры и проекторы. Некоторые из этих инструментов производят виртуальное изображение при нанесении на человеческий глаз; другие производят реальное изображение что можно запечатлеть на фотопленка или оптический датчик, или их можно просмотреть на экране. В этих устройствах линзы иногда сочетаются с изогнутые зеркала сделать катадиоптрическая система где сферическая аберрация объектива корректирует противоположную аберрацию в зеркале (например, Шмидт и мениск корректоры).

Выпуклые линзы создают изображение объекта на бесконечности в их фокусе; если солнце При отображении изображения большая часть видимого и инфракрасного света, падающего на линзу, концентрируется в небольшом изображении. Большая линза создает достаточную интенсивность, чтобы сжечь воспламеняющийся объект в точке фокусировки. Поскольку воспламенения можно добиться даже с помощью плохо сделанной линзы, линзы использовались в качестве горящие очки минимум 2400 лет.^[7] Современное применение - использование относительно больших линз для концентрировать солнечную энергию на относительно небольших фотоэлектрические элементы, собирая больше энергии без необходимости использовать более крупные и дорогие элементы.

Радиоастрономия и радар системы часто используют диэлектрические линзы, обычно называемый линзовая антенна преломлять электромагнитное излучение в коллекторную антенну.

Линзы могут поцарапаться и поцарапаться. Истирание -устойчивые покрытия доступны, чтобы помочь контролировать это.^[33]

Смотрите также

• Против запотевания обработка оптических поверхностей
• Задняя фокальная плоскость
• Боке
• Кардинальная точка (оптика)
• Каустик (оптика)
• Окуляр
• F-число
• Гравитационная линза
• Линза (анатомия)
• Список дизайнов линз
• Числовая апертура
• Оптические покрытия
• Дизайн оптических линз
• Фотохромная линза
• Призма (оптика)
• трассировка лучей
• Анализ матрицы переноса лучей

Рекомендации

1. Вариант написания линза иногда можно увидеть. Хотя в некоторых словарях он указан как альтернативное написание, в большинстве популярных словарей он не указан как приемлемый.
   • Брайанс, Пол (2003). Распространенные ошибки на английском языке. Франклин, Бидл и партнеры. п.125. ISBN  978-1-887902-89-2. Получено 28 июн 2009. Сообщает "линзу", как указано в некоторых словарях, но в целом не считается приемлемым.
   • Медицинский словарь Мерриам-Вебстера. Мерриам-Вебстер. 1995. стр.368. ISBN  978-0-87779-914-6. Перечисляет "линза" как допустимое альтернативное написание.
   • "Линза или линза - что правильно?". Writingexplained.org. 30 апреля 2017. Анализирует почти незначительную частоту использования и приходит к выводу, что орфографические ошибки являются результатом неправильного сингуляризации множественного числа (линзы).
2. Синиш, Джордж; Сакелларакис, Яннис А. (1987). «Линзы в древности». Американский журнал археологии. 91 (2): 191–196. Дои:10.2307/505216. JSTOR  505216.
3. Белый дом, Дэвид (1 июля 1999 г.). "Самый старый телескоп в мире?". Новости BBC. Получено 10 мая 2008.
4. "Линза Нимруда / Линза Лаярда". База данных коллекции. Британский музей. Получено 25 ноября 2012.
5. Д. Брюстер (1852 г.). «Из-за линзы из горного хрусталя и разложившегося стекла, найденного в Нинивехе». Die Fortschritte der Physik (на немецком). Deutsche Physikalische Gesellschaft. п. 355.
6. Крисс, Тимоти С .; Крисс, Весна Мартич (апрель 1998 г.). «История операционного микроскопа: от увеличительного стекла до микронейрохирургии». Нейрохирургия. 42 (4): 899–907. Дои:10.1097/00006123-199804000-00116. PMID  9574655.
7. Аристофан (22 января 2013 г.) [Впервые исполнено в 423 г. до н.э.]. Облака. Перевод Хики, Уильям Джеймс. Проект Гутенберг. Электронная книга № 2562.[1]
8. Плиний Старший, Естественная история (перевод Джона Бостока) Книга XXXVII, гл. 10.
9. Плиний Старший, Естественная история (перевод Джона Бостока) Книга XXXVII, гл. 16
10. Тилтон, Бак (2005). Полная книга огня: разведение костров для тепла, света, приготовления пищи и выживания. Menasha Ridge Press. п. 25. ISBN  978-0-89732-633-9.
11. Глик, Томас Ф .; Стивен Джон Ливси; Вера Уоллис (2005). Средневековая наука, техника и медицина: энциклопедия. Рутледж. п. 167. ISBN  978-0-415-96930-7. Получено 24 апреля 2011.
12. Аль Ван Хелден. Проект Галилео> Наука> Телескоп. Galileo.rice.edu. Проверено 6 июня 2012 года.
13. Генри К. Кинг (28 сентября 2003 г.). История телескопа. Courier Dover Publications. п. 27. ISBN  978-0-486-43265-6. Получено 6 июн 2012.
14. Пол С. Агуттер; Денис Н. Уитли (12 декабря 2008 г.). Размышляя о жизни: история и философия биологии и других наук. Springer. п. 17. ISBN  978-1-4020-8865-0. Получено 6 июн 2012.
15. Винсент Иларди (2007). Видение эпохи Возрождения от очков до телескопов. Американское философское общество. п. 210. ISBN  978-0-87169-259-7. Получено 6 июн 2012.
16. Микроскопы: временная шкала, Нобелевский фонд. Проверено 3 апреля 2009 г.
17. Фред Уотсон (1 октября 2007 г.). Звездочет: жизнь и времена телескопа. Аллен и Анвин. п. 55. ISBN  978-1-74175-383-7. Получено 6 июн 2012.
18. Этот абзац взят из Британской энциклопедии 1888 года.
19. Грейвенкамп 2004, п. 14
    Hecht 1987, § 6.1
20. Hecht 1987, § 5.2.3.
21. Нейв, Карл Р. «Уравнение тонкой линзы». Гиперфизика. Государственный университет Джорджии. Получено 17 марта 2015.
22. Колвелл, Кэтрин Х. «Ресурсный урок: уравнение тонкой линзы». PhysicsLab.org. Получено 17 марта 2015.
23. «Математика линз». Кабинет физики. Получено 17 марта 2015.
24. Hecht 2002, п. 120.
25. Всегда есть 3 "легких луча". О третьем луче в этом случае см. Файл: Lens3b third ray.svg.
26. Hecht 2002, п. 168.
27. Протип Маллик (2005). "Аксикон" (PDF). Архивировано из оригинал (PDF) 23 ноября 2009 г.. Получено 22 ноября 2007.
28. Grbic, A .; Элефтериадес, Г. В. (2004). «Преодоление дифракционного предела с помощью плоской левой передаточной линзы». Письма с физическими проверками. 92 (11): 117403. Bibcode:2004PhRvL..92k7403G. Дои:10.1103 / PhysRevLett.92.117403. PMID  15089166.
29. Valentine, J .; и другие. (2008). «Трехмерный оптический метаматериал с отрицательным показателем преломления». Природа. 455 (7211): 376–9. Bibcode:2008Натура.455..376В. Дои:10.1038 / природа07247. PMID  18690249. S2CID  4314138.
30. Яо, Цзе; Лю, Чжаовэй; Лю, Юнминь; Ван, Юань; Сунь, Ченг; Бартал, Гай; Стейси, Анжелика М .; Чжан, Сян (15 августа 2008 г.). «Оптическое отрицательное преломление в объемных метаматериалах нанопроволок». Наука. 321 (5891): 930. Bibcode:2008Sci ... 321..930Y. CiteSeerX  10.1.1.716.4426. Дои:10.1126 / science.1157566. ISSN  0036-8075. PMID  18703734. S2CID  20978013.
31. Nielsen, R.B .; Торесон, доктор медицины; Chen, W .; Kristensen, A .; Hvam, J.M .; Шалаев, В. М .; Болтассева, А. (2010). «К суперлинзированию с композитами металл – диэлектрик и мультислоями» (PDF). Прикладная физика B. 100 (1): 93. Bibcode:2010АпФБ.100 ... 93Н. Дои:10.1007 / s00340-010-4065-z. S2CID  39903291. Архивировано из оригинал (PDF) 9 марта 2013 г.
32. Патель, Прачи. «Прощай, изогнутые линзы: новые линзы плоские». Получено 16 мая 2015.
33. Шоттнер, G (май 2003 г.). «Устойчивые к царапинам и истиранию покрытия на пластиковых линзах - современное состояние, текущие разработки и перспективы». Журнал золь-гель науки и технологий. С. 71–79. Дои:10.1023 / А: 1022684011222.

Библиография

• Гехт, Евгений (1987). Оптика (2-е изд.). Эддисон Уэсли. ISBN  978-0-201-11609-0. Главы 5 и 6.
• Hecht, Юджин (2002). Оптика (4-е изд.). Эддисон Уэсли. ISBN  978-0-321-18878-6.
• Грейвенкамп, Джон Э. (2004). Полевое руководство по геометрической оптике. SPIE Field Guides vol. FG01. ШПИОН. ISBN  978-0-8194-5294-8.

внешняя ссылка

• глава из онлайн-учебника по преломлению и линзам
• Тонкие сферические линзы (.pdf) на Проект PHYSNET.
• Артикул объектива на digitalartform.com
• Статья о древнеегипетских линзах
• FDTD Анимация распространения электромагнитного излучения через выпуклую линзу (по оси и вне оси) Видео на YouTube
• Использование увеличительных линз в классическом мире
• Хенкер, Отто (1911). "Линза". Британская энциклопедия. 16 (11-е изд.). С. 421–427. (с 21 схемой)

Симуляции

• Обучение с помощью моделирования - Вогнутые и выпуклые линзы
• OpticalRayTracer - Симулятор объектива с открытым исходным кодом (загружаемый java)
• Видео с имитацией света при прохождении через выпуклую линзу Видео на YouTube
• Анимация, демонстрирующая объектив по QED