Константа связи - Coupling constant

В физика, а константа связи или параметр связи датчика (или, проще говоря, связь), - число, определяющее силу сила проявил в взаимодействие. Обычно Лагранжиан или Гамильтониан системы, описывающей взаимодействие, можно разделить на кинетическая часть и часть взаимодействия. Константа связи определяет силу части взаимодействия относительно кинетической части или между двумя секторами части взаимодействия. Например, электрический заряд частицы - это константа связи, которая характеризует взаимодействие с двумя заряженными полями и одним фотон поле (отсюда и обычная диаграмма Фейнмана с двумя стрелками и одной волнистой линией). Поскольку фотоны опосредуют электромагнитный сила, эта связь определяет, насколько сильно электроны чувствуют такую силу, и ее значение фиксируется экспериментально.

Муфта играет важную роль в динамике. Например, часто устанавливают иерархию аппроксимации на основе важности различных констант связи. В движении большого куска намагниченного железа магнитные силы могут быть более важными, чем силы тяжести, из-за относительных величин констант связи. Однако в классическая механика, эти решения обычно принимаются непосредственно путем сравнения сил.

Постоянная тонкой структуры

Муфты возникают естественным образом в квантовая теория поля. Особую роль в релятивистских квантовых теориях играют связи, которые безразмерный; т.е. являются чистыми числами. Примером такой безразмерной постоянной является постоянная тонкой структуры,

{ displaystyle alpha = { frac {e ^ {2}} {4 pi varepsilon _ {0} hbar c}},}

где $е$ это заряд электрона, ${ displaystyle varepsilon _ {0}}$ это диэлектрическая проницаемость свободного пространства, ℏ - приведенная постоянная Планка и $c$ это скорость света. Эта постоянная пропорциональна квадрату силы связи заряда электрона с величиной электромагнитное поле.

Манометрическая муфта

В неабелевом калибровочная теория, то параметр связи датчика, ${ displaystyle g}$ , появляется в Лагранжиан так как

{ displaystyle { frac {1} {4g ^ {2}}} { rm {Tr}} , G _ { mu nu} G ^ { mu nu},}

(где г калибр поле тензор) в некоторых соглашениях. В другом широко используемом соглашении г масштабируется так, чтобы коэффициент кинетического члена был 1/4 и ${ displaystyle g}$ появляется в ковариантная производная. Следует понимать, что это похоже на безразмерную версию элементарный заряд определяется как

{ displaystyle { frac {e} { sqrt { varepsilon _ {0} hbar c}}} = { sqrt {4 pi alpha}} приблизительно 0,30282212 ~~.}

Слабая и сильная связь

В квантовая теория поля с безразмерной муфтой г, если г намного меньше 1, теория называется слабосвязанный. В этом случае он хорошо описывается разложением по степеням г, называется теория возмущений. Если константа связи порядка единицы или больше, теория называется сильно связанный. Примером последнего является адронный теория сильные взаимодействия (поэтому его в первую очередь называют сильным). В таком случае для исследования теории необходимо использовать непертурбативные методы.

Ходовая муфта

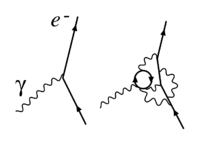
Можно исследовать квантовая теория поля на коротких промежутках времени или расстояниях, изменяя длину волны или импульс, k, используемого зонда. С помощью высокочастотного (т.е. кратковременного) зонда можно увидеть виртуальные частицы участие в каждом процессе. Это очевидное нарушение сохранение энергии можно понять эвристически, исследуя отношение неопределенности

{ displaystyle Delta E Delta t geq { frac { hbar} {2}},}

что фактически позволяет такие нарушения в короткие сроки. Предыдущее замечание относится только к некоторым формулировкам квантовой теории поля, в частности, каноническое квантование в картинка взаимодействия.

В других формулировках это же событие описывается «виртуальными» частицами, вылетающими из массовая оболочка. Такие процессы перенормировать связь и сделать ее зависимой от шкалы энергии, μ, на котором исследуют муфту. Зависимость муфты г (μ) в энергетической шкале известен как «работа муфты». Теория работы муфт дается ренормгруппа, хотя следует иметь в виду, что ренормализационная группа - это более общее понятие, описывающее любые вариации масштаба в физической системе (подробности см. в полной статье).

Бета-функции

В квантовой теории поля a бета-функция, β(г), кодирует работу параметра связи, г. Он определяется соотношением

{ displaystyle beta (g) = mu { frac { partial g} { partial mu}} = { frac { partial g} { partial ln mu}},}

где μ - энергетический масштаб данного физического процесса. Если бета-функции квантовой теории поля обращаются в нуль, то теория масштабно-инвариантный.

Параметры связи квантовой теории поля могут течь, даже если соответствующие классические поле теория масштабно-инвариантный. В этом случае ненулевая бета-функция говорит нам, что классическая масштабная инвариантность равна аномальный.

КЭД и полюс Ландау

Если бета-функция положительна, соответствующая связь увеличивается с увеличением энергии. Примером является квантовая электродинамика (QED), где можно найти, используя теория возмущений что бета-функция положительный. В частности, при низких энергиях α ≈ 1/137, а в масштабе Z-бозон, около 90ГэВ, один измеряет α ≈ 1/127.

Более того, пертурбативная бета-функция говорит нам, что связь продолжает увеличиваться, и QED становится сильно связанный при высокой энергии. Фактически связь, по-видимому, становится бесконечной при некоторой конечной энергии. Это явление впервые было отмечено Лев Ландау, и называется Полюс Ландау. Однако нельзя ожидать, что пертурбативная бета-функция даст точные результаты при сильной связи, и поэтому вполне вероятно, что полюс Ландау является артефактом применения теории возмущений в ситуации, когда она больше не действует. Истинное поведение масштабирования ${ displaystyle alpha}$ при больших энергиях неизвестно.

КХД и асимптотическая свобода

В неабелевых калибровочных теориях бета-функция может быть отрицательной, как впервые было обнаружено Франк Вильчек, Дэвид Политцер и Дэвид Гросс. Примером этого является бета-функция для квантовая хромодинамика (КХД), и в результате связь КХД уменьшается при высоких энергиях.

Кроме того, связь уменьшается логарифмически, явление, известное как асимптотическая свобода (открытие которого награждено Нобелевская премия по физике в 2004 г.). Связь уменьшается примерно как

{ displaystyle alpha _ { text {s}} (k ^ {2}) { stackrel { mathrm {def}} {=}} { frac {g _ { text {s}} ^ { 2} (k ^ {2})} {4 pi}} приблизительно { frac {1} { beta _ {0} ln left ({ frac {k ^ {2}} { Lambda ^ {2}}} right)}},}

где β₀ - константа, впервые вычисленная Вильчеком, Гроссом и Политцером.

И наоборот, связь увеличивается с уменьшением энергии. Это означает, что связь становится большой при низких энергиях, и больше нельзя полагаться на теория возмущений.

Шкала КХД

В квантовая хромодинамика (КХД) величина Λ называется Шкала КХД. Ценность

{ displaystyle Lambda _ { rm {MS}} = 218 pm 24 { text {МэВ}}.}

^{[нужна цитата ]}

Это значение следует использовать на шкале над нижним кварк масса около 5ГэВ. Смысл минимальное вычитание (МС) масштаб схемы Λ_РС приведено в статье о пространственная трансмутация.

В отношение масс протона к электрону в первую очередь определяется шкалой КХД.

Теория струн

Совершенно иная ситуация существует в теория струн поскольку он включает дилатон. Анализ струнного спектра показывает, что это поле должно присутствовать либо в бозонная струна или NS-NS сектор суперструна. С помощью вершинные операторы, можно увидеть, что возбуждение этого поля эквивалентно добавлению члена к действию, где скалярное поле пары в Скаляр Риччи. Таким образом, это поле представляет собой целую функцию констант связи. Эти константы связи не являются заранее определенными, регулируемыми или универсальными параметрами; они зависят от пространства и времени динамически определяемым образом. Источники, которые описывают соединение струн, как если бы оно было исправлено, обычно относятся к ожидаемое значение вакуума. Это может иметь любую ценность в бозонной теории, где нет сверхпотенциал.

Смотрите также

использованная литература

Введение в квантовую теорию поляМ.Е. Пескина и Х.Д. Шредера, ISBN 0-201-50397-2